面向GMTI任务的系绳式InSAR系统展开研究
2016-11-20张锦绣张志刚
张锦绣, 张志刚
哈尔滨工业大学 航天学院, 哈尔滨 150001
面向GMTI任务的系绳式InSAR系统展开研究
张锦绣*, 张志刚
哈尔滨工业大学 航天学院, 哈尔滨 150001
研究了短绳系式合成孔径雷达干涉技术(InSAR)系统面向地面动目标检测(GMTI)任务时的展开问题。使用系统的三维动力学模型,首先分析系统在平衡位置附近的稳定性,确定系统执行GMTI任务时面临的问题。结合GMTI任务需求确定系统短系绳情况时的展开方式,使用粒子群算法对系统初始分离速度和方向进行优选,使系统在展开结束时恰好摆动到水平方向。在展开完成后对系统施加阻尼控制和喷气控制,使系统长期处于水平方向附近,以获取期望顺轨基线,最后通过数值仿真验证。结果表明:考虑展开机构静摩擦力时,在优选的初始状态下无控展开,系统能够到达目标位置,且在稳定控制下能够长期保持顺轨基线大于99.6 m。
系绳式InSAR系统; GMTI任务; 稳态性能分析; 粒子群算法; 稳定控制
合成孔径雷达干涉技术(InSAR)因其能够全天时、全天候的探测而得到广泛应用[1-2],其中一项是地面动目标检测(GMTI),能够大面积侦察、检测、跟踪、定位地面动目标,有着重要的军事应用价值[3-4]。GMTI系统沿航向编队时基线性能最优[5],但实际上稳定的沿航向编队难以实现,其他编队如Cartwheel[6]在运行过程中顺轨基线变化很大,切航迹基线亦较大,不适合GMTI任务。相比于分布式SAR系统[7-8]周期性变化的基线,绳系InSAR系统可在较长时间内提供相对稳定的顺轨基线,且在轨展开时间较短。
在以往研究中,空间系绳被应用到不同的太空任务中,如轨道转移[9]、轨道维持[10]、太空舱返回[11]和卫星离轨[12]等。部分任务对系绳分布方向不作要求,但多数系统希望系绳能够沿铅垂方向分布,以利用重力梯度力矩保持稳定。系绳式InSAR系统执行GMTI任务需要沿水平方位分布以使切航迹基线最小化,相比其他任务,其对系统空间构型要求独特。在系绳式InSAR任务中,系统快速且稳定地成功展开是完成任务的前提。尽管针对空间绳系SAR任务的研究较少,但已有诸多学者针对普适性绳系卫星系统,尤其是展开控制[13-17]方面开展了大量研究,提出了绳长速率控制、系绳张力反馈控制和最优展开控制等方法。但多数研究中系绳较长,系统展开开始阶段展开执行机构不工作,只有当系绳伸展到一定长度后重力梯度力矩能够克服执行机构输出误差时才按照各种控制律开始工作。然而GMTI任务需求顺轨基线较短,仅为几百米,甚至更短,系统重力梯度力矩较小,为避免展开提前停止,短系绳系统在展开时展开执行机构不工作,且应考虑系统展开执行机构的静摩擦力。此时系统展开对于初始参数的依赖增强,而以往关于空间系绳的展开较少关注系统的初始参数选择问题。
本文针对面向GMTI任务的短绳系InSAR系统,考虑系绳的弹性和摆动,使用系统三维运动模型,确定系统的平衡位置,分析系统在任务要求位置附近的稳定性。然后结合系统任务分析系统展开要求,确定对系统展开初始参数的要求,使用粒子群算法对初始参数进行优选。展开完成后使用被动阻尼器控制系绳的高频振荡,使用喷气控制系统的面内摆动,将其稳定在水平位置附近以获取满足任务要求的顺轨基线。
1 系绳式InSAR动力学模型
在本文研究的系绳式InSAR系统中,主星和子星的质量基本相当,且远大于系绳质量,系统质心可近似认为在两颗卫星质心连线上。系绳长度与需求基线长度相当,由GMTI任务需求确定。不过一般GMTI要求顺轨基线较短,故系绳长度亦较短,系绳所受大气阻力较小,产生的大气阻力力矩也较小,可作为扰动处理。同时为了简化系统动力学模型,作出如下合理假设:将卫星视为质点,认为卫星姿态可控,不会因为卫星姿态失稳滚转而导致展开失败;系统质心轨道为Keplerian轨道;忽略系绳的扭转和弯曲。
系绳式InSAR系统简化模型如图1所示,其中c-xyz为系统质心轨道坐标系,Mm和Ms分别表示主星和子星,v为系统质心速度,θ和φ分别为系统的面内摆角和面外摆角。在系统质心轨道坐标系c-xyz中,其动力学方程可以表示为[11]
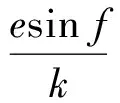

(1)
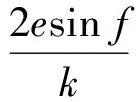

(2)
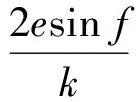


(3)

系统质心轨道方程为
(4)
式中:μ为地球引力常数;a为系统质心轨道半长轴。

图1 系绳式InSAR系统简化模型Fig.1 Simplified model of tethered InSAR system
2 水平方位稳定性分析
系绳式InSAR系统执行GMTI任务的理想位置是沿水平方向分布。为获取系统在水平方向附近的稳定性,为后续展开和控制提供定性分析,首先求解系统的平衡位置,并分析系统在平衡位置附近的稳定性。系统处于稳定状态时,系统状态为
(5)
θe=ce1,φe=ce2,Λe=ce3
(6)
式中:θe、φe和Λe分别为系统处于平衡位置时的系统状态,式(5)中为与之对应状态的速度和加速度,下标e表示系统处于平衡位置时的状态;cei(i=1,2,3)为任意常数。
此时系统不受外力作用,系统动力学方程可写为
2esinf=3sinθecosθe
(7)
sinφecosφe=0
(8)


(9)
式中:系绳张力可以表示为Te=EA(Λe-1),E为系绳杨氏模量,A为系绳横截面积,EA为系绳刚度。
由式(8)可知,系统面外平衡角φe与其他状态量无关,故可首先确定系统的面外摆角平衡点为:φe=±iπ/2(i为任意整数)。i为偶数时,cos2φe=1;i为奇数时,cos2φe=0。根据式(9),为使系绳保持张紧,需Te≥0 N,i只能为偶数,因此处于平衡位置时系统在质心轨道平面内。
由式(7)可知,系统的面内摆动平衡点与轨道偏心率有关,且随着系统质心真近点角的变化而变化。当e=0,即系统质心轨道为圆轨道时为一特例,此时系统面内摆动平衡点为:θe=±iπ/2(i为任意整数),即平衡位置沿铅垂或水平方向分布。i为偶数,系绳沿铅垂方向分布时,有

当i为奇数,即系绳沿水平方向分布时,Te=0 N。可见当系统沿水平方向分布时系绳不起作用。
由式(7)可知,系统质心轨道为椭圆轨道时,系统平衡位置不再沿铅垂或水平方向分布,且系统质心轨道偏心率越大,整个轨道周期内系统平衡位置偏离铅垂或水平方向的角度越大。系统平衡位置与轨道偏心率及真近点角的关系见图2,图中平衡位置偏离角度与式(7)一致,另外每个时刻系统的平衡位置有4个,图中仅给出θe在0° 和90° 附近的变化情况,其在180° 和-90° 附近变化规律亦如此,此处略去。
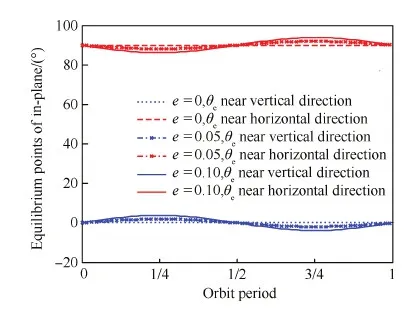
图2 系统平衡位置与轨道偏心率及真近点角的关系Fig.2 Relationship between equilibrium with ecctricity and true anomaly
系统平衡位置若要在水平方向附近,系统轨道偏心率应较小。f∈(0,π/2)∪(3π/2,2π)时,Te>0 N;f∈(π/2,3π/2)时,系绳沿铅垂方向分布时Te>0 N,系绳沿水平方向分布时Te≤0 N。
GMTI任务需要获取顺轨基线,最理想情况是系统沿水平方向分布。系统处于平衡位置时系统的面外摆角为0°,系统在质心轨道面内存在4个平衡位置。为简化分析,只考虑系统面内运动,此时系统状态变量为
将系统在平衡位置小范围近似线性化,可得
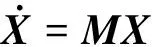
(10)
式中:
上述方程中包含系绳质量的项较多,而系绳质量相比于卫星质量较小,即mt/m≪10,忽略系绳质量可以简化分析。此时系数矩阵M为
(11)
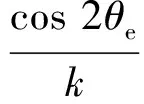
系统特征方程为
[λ(λ-2Q3)+3Q1][λ(λ-2Q3)-Q4]=0
(12)
可得系统特征值为
(13)
式中:
由式(13)可见,运行在椭圆轨道的系统在平衡位置附近的稳定性不仅与系统的真近点角相关,而且还和系统平衡位置相关,系统的平衡位置又与轨道偏心率和真近点角相关。当系统平衡位置在水平方向附近时,cos 2θe<0,可得H1>e2sin2f,故系统特征值必有正值,因此系统沿水平方向分布时不稳定。然而面向GMTI任务的系绳式InSAR需要沿水平方向分布,因此最好能够将系统展开到水平方向并施加控制,使其在水平方向附近运动。
3 系统面向GMTI任务的展开分析
本文研究对象为携带X波段的SAR系统,为高精度测量地面运动目标,需要顺轨基线约100 m。因此系绳展开长度设定为100 m,由于系绳长度较短,系统重力梯度力矩较小,若使用滚轮等展开机构容易因为其输出误差导致系统展开阻力较大,甚至提前停止,故本文选择自由展开方式。系统展开流程为:展开前,两颗卫星结合在一起,通过弹射分离机构使系统分离,系统自由展开,当系统展开水平方位时施加控制,使系统停留在水平方位附近。为了使系统快速展开到期望位置,需要对系统弹射分离的速度和方向进行优选。系统展开时展开机构存在静摩擦力,初始分离速度需要大于某一个值,以避免在展开完成前停止,但并不是越大越好,较大的初始速度会导致展开完成时剩余速度较大,引发系绳纵向高频振荡,严重时系统会发生碰撞,因此需要选择一个尽量小的初始分离速度。由于系统的面外运动和面内运动耦合较弱,面外初始摆角较小时,后续的面外摆角也较小且逐渐衰减,故假定系统面外摆角和角速度均零,即φ=0 rad,φ′=0 rad/s,系统的运动方程简化为面内运动方程,即

(14)
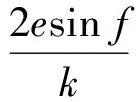
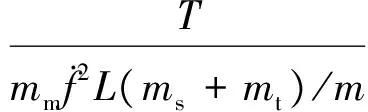
(15)
为使系统在无控条件下均能完成展开,系统的展开速度应大于某一值,使其能够在最恶劣情况下展开到目标长度时速度刚好衰减到零,此时的初始展开速度能够满足任意初始角度。最恶劣情况下系绳变化方程为

参加会议的费用,一般包括会务费(少数会议没有此费用)、交通费及住宿费等,少则几百,多则几千,可以利用个人或团队的科研经费,也可向图书馆领导申请。一般和本职工作密切相关的会议或有会议征文获奖的,馆领导都会同意出资。例如笔者是采编部主任,所参加的文献资源建设方面的相关会议都是馆里资助的,其他会议大多是走个人或团队的科研经费。
(16)

完成系统初始分离速度的优选后,还需要对初始分离角度进行优选,以使系统展开完成时刚好摆动到水平方向。选择系统初始分离方向优选指标为
J=θf-π/2
(17)
式中:θf为系统展开结束时的面内摆角。
在动力学方程式(14)和式(15)约束下对系统初始分离角度进行优选,使性能指标式(17)最小。
4 基于粒子群算法的初值优选
粒子群算法[18-19]是一种模拟自然生物群体行为的启发式算法,基于群体单位间相互学习行为。群体中每个个体称为“粒子”,每个粒子代表一个潜在可行解,群体在解空间上搜索最优解,且每个粒子每次搜索都有与之对应的适应度数值,可以用来调整搜索方向,另外群体能够记忆每个粒子的历史最优解和群体历史最优解,每个粒子通过不断学习自身最优解和群体最优解而不断接近最优解。
以在D维空间上搜索的群体为例,粒子i的位置信息表示为Pi=[pi1pi2…piD]T,速度为Vi=[vi1vi2…viD]T。第k次搜索粒子i的位置和速度更新公式为
(18)
(19)
式中:Phi为粒子i的历史最优解;Pg为群体历史最优解;w为惯性权值;c1和c2为学习因子,用来调节粒子i向自身历史最优解和群体历史最优解的靠近速度;cr为随机值。
使用粒子群算法求解最优解的步骤如下:
步骤1初始化。在搜索空间上随机产生N个粒子(N为群体数量)的初始位置和速度,并计算每个粒子的适应度,将当前位置设为粒子的最优解,对比群体中所有粒子的适应度值,将适应度值最小的粒子位置作为群体历史最优解初值。
步骤2更新粒子的位置和速度。按照式(18)和式(19)更新群体粒子的位置和速度。
步骤3评价更新粒子。计算更新后每个粒子的适应度值,如果好于对应粒子历史最优解,则将当前粒子位置更新为历史最优解。将本次更新群体中最好粒子对应的适应度与群体历史最优解对应的适应度比较,如果效果好于后者,则将对应粒子位置更新为群体历史最优解。
步骤4结果判定。若达到最大迭代次数或满足所需适应度,则终止迭代,否则返回步骤2。
粒子群算法在解空间上搜索,相比遗传算法无需编码、解码过程,设置参数少,调整方便,易于实现。
5 系统面向GMTI任务的稳态控制
由于优选的最小初始分离速度是按照最坏情况得到的,实际情况中系绳展开到目标长度后依然有残留速度。虽然这避免了展开末段耗时过长,但也会使系绳产生纵向振荡。根据前面分析知,系统面内运动耦合较强,为使系统能够稳定在水平方向附近,需对系绳的高频振动施加阻尼,使其快速衰减。为了节省能量,此处使用被动阻尼控制方法,通过弹簧阻尼器对系绳振动进行阻尼。为了将系统径向振动与阻尼器之间的能量转移最大化,使阻尼器的固有频率与系绳的固有频率相等[20]。系统展开到目标长度后其径向振动固有频率为
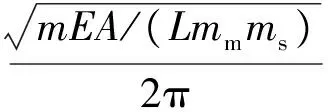
(20)
设计阻尼器参数为

(21)
式中:ξ为阻尼器阻尼系数。
通过对系统初始分离角度的优选使系统在展开到目标长度的同时摆动到水平位置,然而此时系统的面内摆动角速度不为零,需要对系统施加控制力矩使系统的摆动角速度变为零,此处选用喷气控制提供控制力矩,由于控制时间较短,可近似视为脉冲控制。另外系绳无法提供弯曲力矩,需要两颗卫星同时喷气来分别控制,每颗卫星所需改变动量为

(22)

运行在圆轨道的系统沿水平方向是临界稳定的,系统状态稍微偏离平衡点,系统便会偏离水平方位,而实际中无法使系统刚好位于平衡位置。而运行于椭圆轨道的系统沿水平方向分布是不稳定的,在后续运行过程中系统会偏离水平方位,且系统切轨分量会随着偏离角度的增大而增大,当系统切轨分量较大时会对GMTI任务造成干扰,因此需要对系统的面内摆角施加控制。由于系统位于水平方向附近时角速度较小,若对系统面内摆角进行实时控制,所需控制量亦较小,实际中不易执行,可选择离散脉冲控制,当系统偏离水平方位某一角度时施加控制力矩,使系统回到水平方位。
本文中设定系统最大且航迹基线为10 m,则相对于100 m的系绳,系统容许面内摆角偏离值约为5°,故当系统偏离水平方位5° 时对系统施加反方向控制力矩使其获得大小相等的反向自转角速度,以回到水平位置。
6 仿真验证
设定系统携带X波段SAR,执行GMTI任务时需要顺轨基线100 m,其他系统参数见表1。

表1 仿真中的系统参数Table 1 System parameters used in simulation

使用优选的初始参数对系统进行展开,展开到目标长度后对系统进行稳定控制。结合文献[21],选择阻尼器阻尼系数ξ=0.9。数值仿真结果见图3~图6。
图3为系统面内摆动图,其中实线部分为系统展开过程中面内摆角变化,可见在该优选初始状态下系统展开到目标长度时恰好摆动到水平方向,所优选的初值能够满足要求。随后使用喷气控制系统的面内摆角,使系统处于水平方向附近,面内摆角85° 和95° 为控制点,控制周期约为0.7个轨道周期。
图4为系统顺轨基线变化情况,系统稳态控制阶段,系统顺轨基线周期性变化,当系统偏离水平方向5° 时系统顺轨基线最短,最小值大于99.6 m,其变化规律与稳态阶段的系统面内摆角变化情况对应。

图3 系统面内摆角变化Fig.3 In-plane angle variation of system
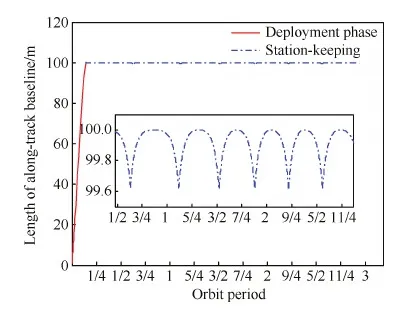
图4 系统顺轨基线变化Fig.4 Length variation of along-track baseline of system
图5为两星径向速度的变化情况,可知系统在展开过程中速度一直减小,这是因为考虑了系统释放机构的静摩擦力。但展开完成时相对速度不为零,这避免了系统末端展开过慢而导致耗时较长,同时也不会因为残余速度过大而导致大幅度振荡。在阻尼器作用下,系统径向高频振荡很快衰减,稳态控制阶段系统径向速度非常小。
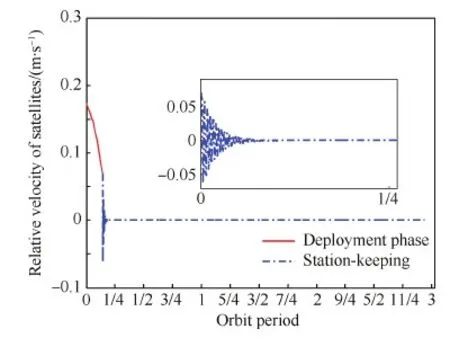
图5 系统径向速度变化Fig.5 Variation of relative velocity along tether

图6 展开完成后系绳张力变化Fig.6 Variation of tether tension after deployment
图6为系绳张力变化情况,展开刚结束时由于径向残余速度导致系绳张力较大,不过随着径向高频振荡的衰减而迅速减小。在稳态控制阶段,系绳张力类周期变化,主要受真近点角影响,与前面的定性分析一致。由图6的放大图可知,系统在平衡位置附近时系绳张力会为零,意味着系绳可能出现松弛现象。这是因为在喷气控制下系统会摆向平衡位置,但是系统接近平衡位置时其相对系统质心转动角速度变小,导致系统离心力减小,另外系绳在恢复力作用下收缩,且收缩到标称长度时速度不为零,导致系绳长度小于标称长度,系绳张力为零。与此同时系统的转动角速度会因为系绳长度的减小而增大,在无控状态下系绳会逐渐张紧,不会出现系绳张力一直为零的情况。另外由动力学方程式(1)~式(3)可知,系绳张力为零时不会对系统姿态产生不利影响,反而会减弱系绳张力对卫星姿态的影响。
由图3~图6可知,使用优选得到的初始参数,系统能够快速展开到目标长度且恰好摆动到水平方向,卫星相对速度亦减小到约0.06 m/s;展开后的阻尼控制能够使系绳高频振荡快速衰减,喷气控制使系统维持在水平方向附近,且控制频率约为0.7个轨道周期。系统的顺轨基线最小为99.6 m,能够满足任务要求。
7 结 论
本文研究了面向GMTI任务的系绳式InSAR系统展开问题,由于系绳较短,系统重力梯度力矩较小,假若展开机构工作可能会因控制误差而导致展开提前停止。故本文在无控状态下展开系统。结合GMTI任务,使用粒子群算法对系统初值进行优选,使其展开到目标长度时恰好摆动到水平方向,并将其控制到水平方向附近。最后通过数值仿真验证优选的初始参数和稳定控制方法。结论如下:
1) 使用粒子群优选的初值能够满足要求,在该初值下无控展开,系统展开速度不会在展开完成前减小到零,且系统在展开到目标长度时恰好摆动到水平位置。
2) 系统展开完成后,使用被动阻尼控制器喷气控制分别控制系统的径向高频振荡和系统面内摆动。系统高频振荡很快衰减,而面内摆角始终在水平方向附近,获取的顺轨基线大于99.6 m,能够满足任务要求。
[1] OUCHI K. Recent trend and advance of synthetic aperture radar with selected topics[J]. Remote Sensing, 2013, 5(2): 716-727.
[2] MOREIRA A, IRAOLA P P, YOUNIS M, et al. A tutorial on synthetic aperture[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6-43.
[3] KAHLE R, RUNGE H, ARDAENS J S, et al. Formation flying for along-track interferometric oceanography—First in-flight demonstration with TanDEM-X[J]. Acta Astronautica, 2014, 99: 130-142.
[4] MOCCIA A, RUFINO G. Spaceborne along-track SAR interferometry: Performance analysis and mission scenarios[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 199-213.
[5] 梁甸农, 蔡斌, 王敏, 等. 星载SAR-GMTI研究进展[J]. 国防科技大学学报, 2009, 31(4): 87-92.
LIANG D N, CAI B, WANG M, et al. Research process of spaceborne SAR-GMTI systems[J]. Journal of National Univeristy of Defense Technology, 2009, 31(4): 87-92 (in Chinese).
[6] MASSONNET D. Capabilities and limitations of the interferometric Cartwheel[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(3): 506-520.
[7] MOCCIA A, VETRELLA S. A tethered interferometric synthetic aperture radar (SAR) for a topographic mission[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(1): 103-109.
[8] BOMBARDELLI C, LORENZINI E C, QUADRELLI M B. Retargeting dynamics of a linear tethered interferometer[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 1061-1067.
[9] 钟睿, 徐世杰. 基于直接配点法的绳系卫星系统变轨控制[J]. 航空学报, 2010, 31(3): 572-578.
ZHONG R, XU S J. Orbit-transfer control for TSS using direct collocation method[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 572-578 (in Chinese).
[10] 刘刚, 李传江, 马广富. 应用非线性模型预测控制的绳系卫星Halo轨道保持控制[J]. 航空学报, 2014, 35(9): 2605-2614.
LIU G, LI C J, MA G F. Station-keeping of tethered satellite system around a halo orbit using nonlinear model predictive control[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2605-2614 (in Chinese).
[11] WILLIAMS P, HYSLOP A, STELZER M, et al. YES2 optimal trajectories in presence of eccentricity and aerodynamic drag[J]. Acta Astronautica, 2009, 64(7): 745-769.
[12] ZHONG R, ZHU Z H. Optimal control of nanosatellite fast deorbit using electrodynamic tether[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1182-1194.
[13] YU S H. Range-rate control algorithms and space rendezvous schemes[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 206-208.
[14] GLABEL H, ZIMMERMANN F, BRUCKNER S, et al. Adaptive neural control of the deployment procedure for tether-assisted re-entry[J]. Aerospace Science and Technology, 2004, 8(1): 73-81.
[15] WILLIAMS P. Optimal deployment/retrieval of tethered satellites[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 324-343.
[16] SUN G H, ZHU Z H. Fractional order tension control for stable and fast tethered satellite retrieval[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(6): 2062-2066.
[17] ASLANOV V S, LEDKOV A S. Dynamics of tethered satellite systems[M]. Oxford: Woodhead Publishing, 2012: 65-88.
[18] 徐鹤鸣. 多目标粒子群优化算法的研究[D]. 上海: 上海交通大学, 2013: 4-12.
XU H M. Research on multi-objective particle swarm optimization algorithms[D]. Shanghai: Shanghai Jiao Tong University, 2013: 4-12 (in Chinese).
[19] 沈伋, 韩丽川, 沈益斌. 基于粒子群算法的飞机总体参数优化[J]. 航空学报, 2008, 29(6): 1538-1541.
SHEN J, HAN L C, SHEN Y B. Optimization of airplane primary parameters based on particle swarm algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1538-1541 (in Chinese).
[20] LEE N N, ZORN A H, WEST M. Passive vertical stabilization of two tethered nanosatellites with engineered damping[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Reston: AIAA, 2008: 1-16.
[21] LORENZINI E C. A three-mass tethered system for micro-g/variable-gapplications[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(3): 242-249.
张锦绣男, 博士, 教授, 博士生导师。主要研究方向: 分布式航天器系统设计与仿真, 系绳式卫星系统应用研究, 空间垃圾天基主动移除。
Tel.: 0451-86403440-8308
E-mail: jinxiu@hit.edu.cn
张志刚男, 博士研究生。主要研究方向: 航天器动力学与控制, 系绳式InSAR系统。
Tel.: 0451-86402357-8503
E-mail: zhzhghit@126.com
URL:www.cnki.net/kcms/detail/11.1929.V.20160627.0836.002.html
DeploymentresearchoftetheredInSARsystemforGMTImissions
ZHANGJinxiu*,ZHANGZhigang
SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001,China
Thedeploymentoftetheredinterferometricsyntheticapertureradar(InSAR)systemappliedforgroundmovingtargetindication(GMTI)missionsisresearchedinthepaper.Toascertainthecharacteristicofdeployment,thethree-dimensionaldynamicsmodelisapplied,andthesteadystateanalysisispresented.Accordingtothesystemfeature,thefreedeploymentmethodischosentoavoidhaltcausedbytheoutputerrorofcontrolmechanism.Asaresult,thedeploymentissensitivetotheinitialstateofsystem.Hence,particleswarmalgorithmisusedtooptimizetheinitialstatetodeploythesystemalonghorizontaldirectionwhenthedeploymentfulfills.Thenapassivedamperandjetscontrolareusedtomakethesystemstaynearhorizontaldirectioninlong-term.Finally,thenumericalsimulationisexecutedtoverifytheoptimizedinitialstateandthesteadycontrolmethod.Theresultsshowthatthesystemcoulddeploytothetargetpositionwiththeoptimizedinitialstate,andthealong-trackbaselineofsystemisalwaysbiggerthan99.6mwiththestablecontrol.
tetheredInSARsystem;GMTImission;steadystateanalysis;particleswarmoptimization;stablecontrol
2016-01-11;Revised2016-04-11;Accepted2016-06-14;Publishedonline2016-06-270836
NationalNaturalScienceFoundationofChina(91438202)
.Tel.:0451-86403440-8308E-mailjinxiu@hit.edu.cn
2016-01-11;退修日期2016-04-11;录用日期2016-06-14; < class="emphasis_bold">网络出版时间
时间:2016-06-270836
www.cnki.net/kcms/detail/11.1929.V.20160627.0836.002.html
国家自然科学基金 (91438202)
.Tel.:0451-86403440-8308E-mailjinxiu@hit.edu.cn
张锦绣, 张志刚. 面向GMTI任务的系绳式InSAR系统展开研究J. 航空学报,2016,37(10):3083-3091.ZHANGJX,ZHANGZG.DeploymentresearchoftetheredInSARsystemforGMTImissionsJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3083-3091.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0186
V476.5
A
1000-6893(2016)10-3083-09
