竖直圆管内超临界碳氢燃料换热恶化的直径效应
2016-11-20程泽源朱剑琴李海旺
程泽源, 朱剑琴, 李海旺
北京航空航天大学 能源与动力工程学院 航空发动机气动热力国家级重点实验室, 北京 100083
竖直圆管内超临界碳氢燃料换热恶化的直径效应
程泽源, 朱剑琴*, 李海旺
北京航空航天大学 能源与动力工程学院 航空发动机气动热力国家级重点实验室, 北京 100083
利用Fluent对超临界压力下直径对碳氢燃料换热恶化的影响进行数值研究,湍流模化采用Launder-Sharma(LS)低雷诺数模型,物性采用广义对应态法则对RP-3替代燃料计算。计算条件:系统压力为3 MPa,进口温度为573 K,热流密度为500 kW/m2,质量流量为0.001 5和0.003 0 kg/s,直径范围为1~10 mm。正常换热条件下的计算壁温和实验结果基本吻合,证明了计算方法的准确度。结果表明:强制对流下小质量流量时直径越大,换热恶化程度更高且更提前发生,换热恶化是由定压比热容处于极大值后的急剧下降区导致的,大质量流量时直径与壁温成正比,无换热恶化发生;浮升力效应仅在小质量流量下起作用,随着直径增大而加强,给出RP-3流动换热时浮升力起作用的判据和不同直径下换热恶化的边界。
超临界; 碳氢燃料; 换热恶化; 直径; 浮升力
超燃冲压发动机面临的关键问题之一是燃烧室冷却问题,高超声速气流产生的气动加热可使发动机进气总温达3 000 K以上,需采用主动冷却方式以保证燃烧室可靠工作[1]。碳氢燃料在吸收燃烧室的热量之后进入燃烧室中燃烧,使吸收的能量返回到做功循环中,因此也称为再生冷却,其显著特征是碳氢燃料工作在超临界压力,超临界压力下流动换热呈现出和亚临界压力下相比特殊的规律,应进行深入的研究[2]。
换热恶化是发生在超临界状态的特有现象,表现为高热流密度下的壁温升高和对流换热系数的下降,壁温的急剧升高使得材料失效,实际工作需避免换热恶化的发生[3]。尽管国内外学者用数值模拟和试验测量的方法从换热恶化的起始点、物性效应、工况影响和传热关联式等角度对换热恶化进行了大量研究[4-7],但对换热恶化的机理仍未形成统一的定论。目前对换热恶化的研究大多数针对水和二氧化碳,对碳氢燃料的研究较少[8-9]。
少数研究者考虑流动换热的几何影响,Shiralkar和Peter[10]对不同直径下超临界CO2在竖直管中的流动换热进行了试验研究,结果发现直径从6.35 mm减小到3.175 mm时,壁温峰值的陡峭程度减弱,同时壁温峰值降低,换热恶化减弱。Zhi和Shuo[11]采用STAR-CD求解器研究了水平圆管超临界水流动换热的直径效应,发现大直径(10 mm)管受到较强的浮升力影响,直径增大,换热恶化的程度增加,随着质量流率的增大,换热恶化现象减弱甚至消失。
本文利用Fluent对超临界压力下碳氢燃料在不同直径的圆管中的流动换热进行数值模拟,探究直径对换热恶化的影响,分析换热恶化的机理并提出直径和换热恶化起始点之间的关联式,为再生冷却技术设计提供参考。
1 超临界碳氢燃料特性
在某一压力下,随着温度升高,液体发生汽化反应变为气体,当压力增大至某一值后,温度升高不再产生相变过程,此时压力称为临界压力。当压力超过临界压力时,流体的热物性随着温度变化呈现出特殊的规律,其中定压比热容随着温度升高出现先上升后下降的趋势,峰值点对应的温度称为拟临界温度。
本文选择碳氢燃料RP-3作为研究工质,利用广义对应态法则对其替代模型的热力学特性和输运特性进行数值模拟,详细的计算方法和数据验证见文献[12]。
在拟临界温度附近,密度、黏度和导热系数迅速减小,随着压力的增大,拟临界温度附近的物性变化减弱甚至消失。超临界压力下物性随温度的特殊变化规律使得流动和换热高度耦合,导致超临界压力下RP-3的流动换热规律更加复杂。
计算得到的RP-3的临界压力为2.43 MPa,临界温度为643.5 K,而试验测得RP-3的临界压力和临界温度分别为2.33 MPa和645.04 K[13],进一步证明物性模型的准确性。
2 数值模化
本文采用ANSYS FLUENT 14.5 对超临界流动换热进行数值模拟,以下依次从物理模型、控制方程、湍流模化、计算网格和数值方法等方面介绍。
2.1 物理模型
图1为物理模型的示例剖面图,R为半径。本文的研究对象为一竖直向上流动圆管,总长为450 mm,管壁厚为0.2 mm,内径范围由1~10 mm。为消除进出口效应以保证流体充分发展,管道进口起始段设置90 mm绝热段,中间300 mm为加热段,剩余60 mm为绝热段。
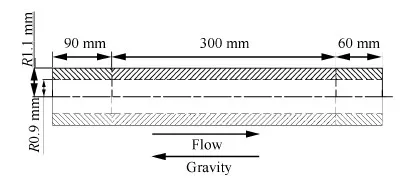
图1 物理模型剖面图Fig.1 Physical model profile
为研究直径对超临界碳氢燃料换热恶化的影响,不同计算工况下保持除直径外的其他几何尺寸不变。研究表明,管壁导热对换热的影响较小[8],因此保持管壁厚不变,仅研究内径变化造成的影响。管道材料为不锈钢,考虑导热系数随温度的变化,使用如下公式计算管壁导热系数:
λ=15.035 43+0.011 78×(T-273.15)+
4.208 54×10-6×(T-273.15)2
(1)
式中:T为温度,λ为导热系数。
2.2 控制方程
由于超临界压力下特殊的物性变化规律,采用守恒型控制方程。本文仅研究超临界压力下稳态流动换热,故所有控制方程不含非稳定项。连续方程、动量方程和能量方程的张量形式如下所示:
连续方程:
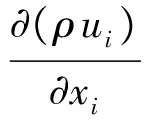
(2)
式中:ρ为密度;ui为速度;xi为坐标。
动量方程:
(3)
式中:gi为重力加速度;P为压力;μ为黏度;δij为克罗内克符号。

(4)
式中:k为湍动能;μt为湍流粘性系数。
能量方程:
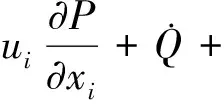
(5)

本文不考虑高温化学反应(即忽略800 K以上逐渐显著的热裂解反应),变物性流动能量方程中压力项和耗散项可忽略[14],则能量方程简化为
(6)
对流换热系数h为

(7)
式中:q为壁面热流密度;Tw为壁面温度;Tb为流体截面平均温度。
2.3 湍流模化
超临界湍流模化是超临界湍流流动模拟的关键,尚无专门用于模拟超临界流动的湍流模型。国内外研究者采用各类已有湍流模型对超临界换热强化和换热恶化的现象进行数值模拟,发现能较好地定性预测超临界换热,然而不同湍流模型在对其定量预测上表现不一[15]。研究表明,低雷诺数k-ε湍流模型是模拟超临界湍流流动较准确的模型,Kim等[16]采用多种湍流模型预测超临界混合对流的直接数值模拟(Direct Numerical Simulation, DNS)结果,发现Launder-Sharma(LS)模型能较好地预测超临界换热,另外本课题组最近的研究结果表明LS模型在模拟超临界碳氢燃料对流换热时效果较好,因此本文采用LS低雷诺数k-ε湍流模型来模化湍流[17],湍流方程如下所示:
本构方程:
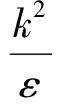
(8)
式中:Cμ为常数;fμ为阻尼函数;ε为湍动能耗散率。
湍动能方程:
ρε-Sk
(9)
式中:σk为湍动能Pr数;Pk和Gk分别为剪应力和浮升力引起的湍动能产生项;Sk为湍动能方程源项。
湍动能耗散率:
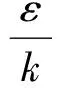
(10)
式中:σε为湍动能耗散率Pr数;Cε1和Cε2分别为常数;f1和f2为函数;Sε为湍动能耗散率方程源项。
Pk为
(11)
本文采用简单梯度扩散(Simple Gradient Diffusion Hypothesic, SGDH)[16]来模化浮升力对湍流的直接效应,
(12)
式中:β为热膨胀系数。
LS模型的常数、函数、源项和边界条件见表1~表3。

表1 LS模型常数Table 1 Constants in LS model

表2 LS模型函数Table 2 Functions in LS model
表3LS模型附加项和边界条件
Table3AdditivetermsandboundaryconditionsinLSmodel

SkSεBoundaryconditiononthewall2uky()22uut2Vx2()2ky()w=0,εw=0
2.4 计算网格
研究模型为轴对称模型,考虑到边界条件的对称性,本文仅计算对称轴截面的一半区域(如图1 的上半部分)。二维结构化计算网格从对称轴延续到固体外壁面,对加热段和壁面处网格加密,获得典型网格无关解(10+70)×(60+250+40),代表(径向固体+流体)×(轴向绝热段+加热段+绝热段),网格数为28 000。
网格无关解计算主要考虑温度和对流换热系数,计算结果如图2所示。由图2可见,在网格数为28 000时,监测变量的变化率小于1%,此时已达到网格无关解。流体域壁面处网格高度增长率设置为1.05,并保证壁面处第1层网格高度y+<1以满足低雷诺数k-ε模型要求。
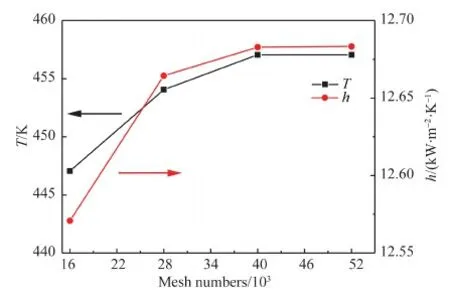
图2 温度和对流换热系数随网格数的变化 Fig.2 Variation of temperature and heat transfer coefficient with mesh numbers
2.5 数值方法
本文采用基于压力求解器求解离散化控制方程,利用SIMPLE算法求解压力速度耦合问题。采用二阶迎风格式计算动量方程和能量方程中的对流项以增加精度,采用一阶迎风格式计算湍流方程的对流项以保持鲁棒性。所有控制方程的收敛标准为残差小于10-6[18]。
考虑到流动过程中压差很小,热物性参数作为温度的函数嵌入到Fluent。选择质量流量进口作为进口边界条件,出口边界条件选为压力出口。管道轴选轴作为边界条件,意味着此处任何变量ϖ满足
(13)
式中:r为管道中心到壁面的距离。
3 计算结果与分析
浮升力是导致换热恶化的重要因素之一,为研究换热恶化的直径效应机理,计算按是否考虑重力分为两部分,分别为强制对流和真实对流。
3.1 计算方法验证
利用试验数据对计算方法进行验证,以确保计算方法可靠准确。张春本[19]对超临界RP-3在内径为1.8 mm的竖直圆管中向下流动换热进行试验研究,试验工况:工作压力为5 MPa,进口温度为373 K,质量流量为0.003 0 kg/s,壁面热流密度分别为300、400和500 kW/m2。
利用前述计算方法对试验结果进行数值模拟,获得了加热段壁温随无量纲长度x/d的变化如图3所示,其中x为距加热段起始点的距离,d为内径。
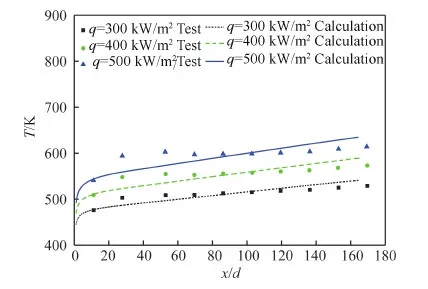
图3 不同热流密度下计算壁温与试验结果对比Fig.3 Contrast between computed wall temperature and test results
从图中可以看出,不同热流密度下,计算结果均较好地预测出试验壁温随着无量纲长度的变化情况。当壁面热流密度q=300、400 kW/m2时,计算和试验结果差别很小,当壁面热流密度q=500 kW/m2时,最大误差为5.8%,平均误差小于3%,误差处于允许范围之内,表明数值计算方法具有较高的精度。较大热流密度时,壁温越接近拟临界温度,此时替代物性模型对真实RP-3的剧烈物性变化的预测水平降低,同时考虑到湍流模化带来的误差,因此综合效果导致对试验结果中的加热起始段效应预测产生误差。
3.2 强制对流下换热恶化
3.2.1 换热恶化机理
图4显示了RP-3在强制对流条件下壁温和对流换热系数随着加热段无量纲长度的变化情况。计算模型选择内径1.6 mm管道,系统压力为3 MPa,进口温度为573 K,壁面热流密度为500 kW/m2,质量流量为0.001 5 kg/s。

图4 壁温和对流换热系数沿管长的变化 Fig.4 Variation of wall temperature and heat transfer coefficient with tube length
由图4可以看出,加热段起始段壁温相对较低,为670 K左右,沿流向方向壁温逐渐上升,在x/d=70处上升速度加快,在x/d=110时到达最大值880 K左右,之后内壁温开始下降;相应的对流换热系数在加热起始段处在较高的水平,沿流向方向先下降,在x/d=110处时达到最低点,之后开始回升,高的壁温和低的对流换热系数这种特殊的现象称为换热恶化,此计算工况可以认为是整个管长均处在换热恶化区间内。
为研究强制对流下换热恶化的机理,加热段管长内不同截面上的密度、定压比热容、速度和湍动能随着无量纲半径的变化如图5~图8所示。选取的截面为x/d=12、43、75、110、137和168,x/d=12对应着换热恶化的起始点,x/d=43、75对应着换热恶化的发展,x/d=110对应着换热恶化的极大点,x/d=137、168对应着换热恢复段。
从图5(a)可以看出,不同截面上定压比热容Cp均从管道中心到管壁面先增加后减小,在某一半径处达到峰值,在x/d=12时,壁温刚刚超过拟临界温度659 K,定压比热容峰值基本贴近壁面,增强了壁面处的吸热能力,使得对流换热系数较高;沿着向下游流动方向,定压比热容峰值逐渐向管道中心移动,壁面处的定压比热容开始减小,当x/d=110、137时,壁面处较低的定压比热容区完全覆盖了热边界层,降低了壁面处的吸热能力,使得对流换热系数处在极小的水平;当x/d=168时,定压比热容已无明显的峰值现象,换热恢复受到流动的直接影响。
从图5(b)可以看出,在x/d=12时,密度在壁面附近变化剧烈,随着流动截面向下游推进,密度剧烈变化区域从壁面向管道中心移动,同时范围变宽,当x/d=168时,密度的剧烈变化现象基本消失,密度值整体减小。连续性原理表明密度的特殊分布影响着速度的分布情况。
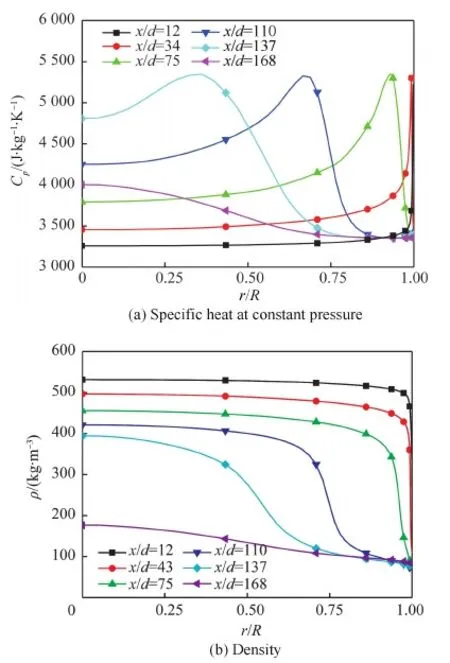
图5 不同截面上定压比热容与密度沿无量纲半径的变化Fig.5 Variation of specific heat at constant pressure and density with dimensionless radius at different cross sections
图6(a)中,U为速度,随着向下游流动,截面上速度型由典型强制对流速度型逐渐变得平坦,当x/d=137时,速度型呈现出“M”分布,这是由物性在拟临界点附近的剧烈变化使得壁面的速度增大,中心处流体速度必须减小从而满足连续性原理。Wood和Smith[20]发现当流体温度在拟临界温度附近时出现“M”型速度分布,图6(a)的结果证明无浮升力时,拟临界温度附近的剧烈物性变化是产生特殊速度分布的诱因。在x/d=137时,速度失稳的程度降低,换热恢复。
从图6(b)看出,x/d=12、43和75处截面上沿整个半径方向上的湍动能都处在较低的水平;随着流动截面向下游推进,壁面处的湍动能明显增加,x/d=137处壁面处的湍动能超出x/d=110处几乎一个量级,湍动能增加导致的换热强化效应大于物性变化引起的换热恶化效应,从而使得换热恢复。

图6 不同截面上速度和湍动能沿无量纲半径的变化Fig.6 Variation of velocity and turbulent kinetic energy with dimensionless radius at different cross sections
3.2.2 直径对换热恶化的影响
在给定物理模型时,质量流量变化会改变流动状态,进而对换热造成影响,以下在两种质量流量工况下进行分析。
1) 小质量流量工况
小质量流量工况包括8组工况,计算模型选择内径1.0~1.7 mm管道,间隔为0.1 mm,系统压力为3 MPa,进口温度为573 K,壁面热流密度为500 kW/m2,质量流量为0.001 5 kg/s。图7给出了不同内径时加热段壁温T随着管长的变化情况,可以看出,在d=1.0 mm时内壁温沿流向基本成线性增加,有轻微的壁温凸升情况出现,此时可认为换热无恶化,随着内径增大,壁温凸升现象逐渐加强,换热恶化现象加强;当内径增大至1.7 mm时,壁温凸升的范围逐渐扩展到整个加热段,壁温峰值增大且向加热段进口移动。
图8给出了不同管径时加热段管道r/R=0.98 处湍动能随着管长的变化情况,从图上看出在d=1.0 mm时,湍动能沿流向方向先线性增加,当x=0.24 mm时变化斜率突然增大,对应着换热的恢复段,在加热段末端到达最大;当内径增大时,湍动能减小,且变化斜率转折点前移,这与内径增大时壁温峰值增大且前移的规律是一致的。

图7 不同内径时壁温随管长的变化Fig.7 Variation of wall temperature with tube length at different inner diameters

图8 不同管径时r/R=0.98处湍动能随管长的变化Fig.8 Variation of turbulent kinetic energy with tube length when r/R=0.98 at different diameters
如前面的分析,定压比热容处在极大值后的急剧下降区是换热恶化的主要原因,大直径下湍流换热能力减弱,壁面处的热流传入主流区的速度减慢,那么壁温增大导致更快进入定压比热容的极大值后的急剧下降区,从而壁温峰值提前。
2) 大质量流量工况
大质量流量工况包括8组工况,计算模型选择内径1.0~1.7 mm管道,间隔为0.1 mm,系统压力为3 MPa,进口温度为573 K,壁面热流密度为500 kW/m2,质量流量为0.003 0 kg/s。图9给出了不同内径时加热段壁温随着管长的变化情况,可以看出,不同内径下加热段壁温沿着流向均呈线性增加,当d=1.6、1.7 mm时在加热段末端出现壁温变化斜率增大的情况;随着内径增大,加热段壁温升高,无换热恶化现象出现,这可理解为加热面积的增大导致的加热热流增加引起的壁温升高。
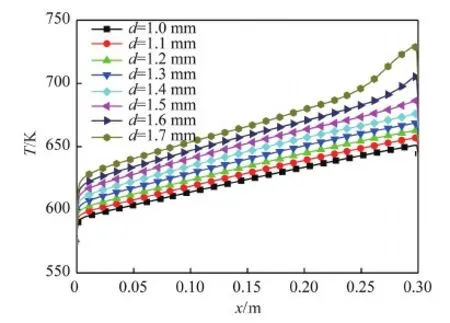
图9 不同内径时壁温随管长的变化Fig.9 Variation of wall temperature along tube length at different inner diameters
图10(a)给出了d=1.7 mm时不同截面上温度随着无量纲半径的变化情况,不同截面上的温度型基本相似,温度在壁面附近发生壁温的降低,在主流区基本保持不变,相似的温度分布意味着主流和壁面之间的温差在流向方向基本一致,表明沿程的对流换热系数没有发生明显的降低,即无换热恶化出现;在x=260 mm时,壁面附近的温度超过了拟临界温度,定压比热容进入了极大值之后的急剧下降区,从而导致了换热能力的轻微下降,对应着图9中d=1.7 mm时加热段末端的壁温变化斜率的增大。
图10(b)给出了d=1.7 mm时不同截面上湍动能随着无量纲半径的变化情况,可以看出不同截面上湍动能的分布趋势基本一致,在壁面处的值在0.11 m2/s2左右,高于图8中d=1.7 mm时湍动能的沿程平均水平,说明了大质量流量时强烈的湍流使得换热恶化不会发生。
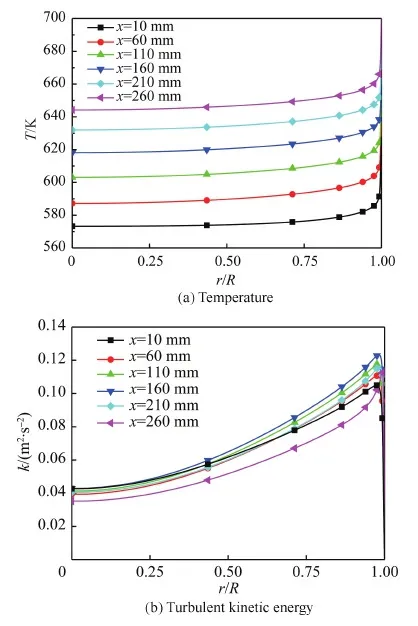
图10 d=1.7 mm时不同截面上温度和湍动能的分布Fig.10 Distributions of temperature and turbulent kinetic energy at different cross-sections when d=1.7 mm
3.3 真实对流下换热恶化
真实对流必须考虑重力的存在,在重力作用下,密度差产生浮升力。超临界下物性的剧烈变化可能会产生特殊的浮升力效应,变物性效应和浮升力效应的共同作用会对超临界流动换热产生复杂的影响。本节在变物性的基础上考虑浮升力效应,首先研究浮升力对换热恶化的影响,之后给出真实对流条件下不同直径下换热恶化的边界。
3.3.1 浮升力对不同直径下换热恶化的影响
图11(a)显示质量流量为0.001 5 kg/s时不同直径下有无重力两种情况下加热段壁温沿管长变化的对比图,直径范围由1 mm到1.7 mm,间隔为0.1 mm。
从图中可以看出,当直径d=1.0 mm时,有重力的计算结果和无重力的计算结果基本一致,表明此时浮升力对换热规律无显著影响,直至d=1.5 mm,两种情况的计算结果出现差异,随着直径的进一步增大,浮升力造成的影响更加显著,有重力情况下壁温峰值相对于无重力的计算结果更高,并更靠近进口处,这表明浮升力加剧了换热恶化的程度,并使得换热恶化的发生点前移,而这种作用仅出现在直径较大的情况,对于直径较小时浮升力基本不起作用。
图11(b)给出了质量流量M为0.003 0 kg/s时不同直径下有无重力两种情况下加热段内壁温沿管长变化的对比图。
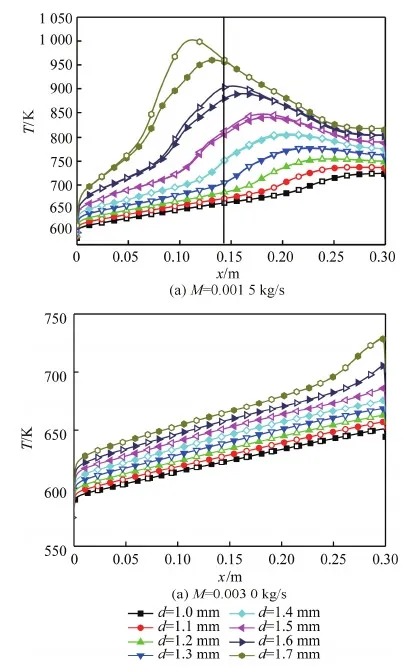
图11 不同直径下加热段内壁温随管长的变化(实心符号代表无重力,空心符号代表有重力)Fig.11 Variation of inner wall temperature with tube length at different diameters (solid: no gravity; hollow: gravity)
从图中看出,不同直径时有无重力两种情况下的曲线均完全重合,证明大质量流量下浮升力对换热无显著影响。
为进一步判断浮升力产生影响的标准,采用浮升力参数Bu来表征浮升力相对于惯性力的大小[21]:
(14)
其中
(15)
式中:Grb为格拉晓夫数;ρ为密度;μ为黏度;下标b为流体截面平均;下标w为壁面。
图12为直径1.7 mm时两种质量流量时Bu数沿管长的分布对比情况,图中竖直黑线x=0.14 m 代表与图11(a)对应的浮升力起作用的边界位置。图11(a)显示1.7 mm管中当x<0.14 m 时,浮升力产生影响,当x>0.14 m时,浮升力的影响可忽略,因此该处的Bu数认为是临界Bu数。

图12 两种质量流量下Bu数沿管长的变化Fig.12 Variation of Bu with tube length at two mass flow rates
可以看出,当Bu数大于4.7×10-6时,浮升力对流动换热有明显的影响,而在大质量流量工况下,Bu数均小于4.7×10-6,因此浮升力对换热无显著作用,如图11(b)所示。文献[21]给出的浮升力起作用的标准是Bu数大于2.0×10-5,这样的差异可能是研究工质的不同造成的,文献[21]中研究工质为二氧化碳,而本文研究的是RP-3替代燃料。
3.3.2 不同直径下换热恶化的边界
为避免再生冷却过程中出现换热恶化,提出不同直径下换热恶化的边界。有学者指出热流密度与质量流率之比q/G可作为换热恶化的阀值参数,当实际q/G大于临界q/G时,换热恶化发生[22]。由于本文研究工况的控制参数为质量流量M,故选择热流密度与质量流量之比q/M表征控制换热恶化发生的参数,并在此基础上研究不同直径下临界q/M的变化规律。
计算模型选择内径1~10 mm的管道,间隔为0.5 mm,系统压力为3 MPa,进口温度为573 K,壁面热流密度为500 kW/m2,质量流量为0.001~0.050 kg/s;最后得到直径与临界q/M之间的关联式为:
(q/M)cr=1.03×108-1.15×107·d+
2.88×108·d-2
(16)
当q/M大于临界q/M时,换热恶化发生;当q/M小于临界q/M时,换热恶化不发生。
为说明所得关联式的物理意义,图13给出了直径与临界质量流量的关系曲线。
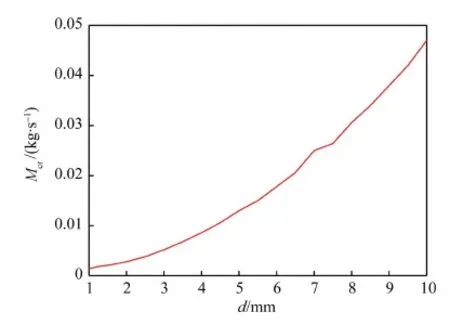
图13 直径与临界质量流量的关系Fig.13 Relationship between diameter and critical mass flow rate
随着直径增大,临界质量流量增大,其变化斜率也逐渐增大,此时M小于Mcr,换热恶化发生。直径增大时,必须提高质量流量以保证流速恒定,因而直径与临界质量流量成正相关,另一方面,直径增大时,浮升力对换热的影响也越明显,体现了关联式中的分母二次项。
4 结 论
1) 强制对流下发生换热恶化的主要原因是定压比热容处于极大值后的急剧下降区,使得流体吸热能力减弱;湍动能的加强使得换热得到逐渐恢复。
2) 强制对流下小质量流量下换热更容易恶化,直径越大,换热恶化加剧并且提前发生;大质量流量下无换热恶化发生,直径越大,壁温越高。
3) 真实对流下浮升力对大质量流量流动工况无显著作用,仅对小质量流量工况起作用,直径越大,浮升力对换热的影响越大,使得换热恶化加剧且发生点向进口处移动。
4) 浮升力起作用的判据标准采用Bu数,当Bu数大于4.7×10-6,浮升力对换热起显著作用;当Bu数小于4.7×10-6,浮升力不起作用。
5) 用热流密度与质量流量之比q/M表征控制换热恶化发生的参数,当q/M大于临界值时,换热恶化发生,当q/M小于临界值时,不发生换热恶化。给出直径与临界q/M的关联式,临界q/M与直径成负相关,随着直径增大,临界q/M的变化斜率减小。
[1] 贺武生. 超燃冲压发动机研究综述[J]. 火箭推进, 2005, 31(1): 29-32.
HE W S. Review of scramjet engine development[J]. Journal of Rocket Propulsion. 2005, 31(1): 29-32(in Chinese).
[2] SOBEI D R, SPADACCIN L J. Hydrocarbon fuel cooling technologies for advanced propulsion[J]. Journal of Engineering for Gas Turbines and Power, 1997, 119(2): 344-351.
[3] SHIRALKAR B S, PETER G. Deterioration in heat transfer to fluids at supercritical pressure and high heat fluxes[J]. Journal of Heat Transfer, 1969, 91(1): 27-36.
[4] MARIA J, HENRYK A. A numerical study of heat transfer to supercritical water flowing upward in vertical tubes under normal and deteriorated conditions[J]. Nuclear Engineering and Design, 2013, 26(4): 61-70.
[5] KOSHIZUKA S, TAKANO N, OKA Y. Numerical analysis of deterioration phenomena in heat transfer to supercritical water[J]. International Journal of Heat and Mass Transfer, 1995, 38(16): 3077-3084.
[6] LEI X L, LI H X, ZHANG Y F, et al. Effect of buoyancy on the mechanism of heat transfer deterioration of supercritical water in horizontal tubes[J]. Journal of Heat Transfer, 2013, 135(1): 1-9.
[7] MAHDI M, MAJID B. New analysis of heat transfer deterioration based on supercritical fluid property variations[J]. Journal of Thermophysics and Heat Transfer, 2012, 26(1): 197-200.
[8] LIU Z Q, LIANG J H, PAN Y. Numerical analysis of heat transfer deterioration of China RP-3 aviation kerosene in a circular tube at supercritical pressures: AIAA-2014-3358 [R]. Reston: AIAA, 2014.
[9] DANG G X, ZHONG F Q, ZHANG Y J, et al. Numerical study of heat transfer deterioration of turbulent supercritical kerosene flow in heated circular tube[J]. International Journal of Heat Transfer, 2015, 85: 1003-1011.
[10] SHIRALKAR B S, PETER G. The effect of swirl, inlet conditions, flow direction, and tube diameter on the heat transfer to fluids at supercritical pressure[J]. Journal of Heat Transfer, 1970, 92(3): 465-471.
[11] ZHI S, SHUO C. Numerical investigation of diameter effect on heat transfer of supercritical water flows in horizontal round tubes[J]. Applied Thermal Engineering, 2011, 31(4): 573-581.
[12] 程泽源, 朱剑琴, 金钊. 吸热型碳氢燃料RP-3替代模型研究[J]. 航空动力学报, 2016, 31(2), 391-398.
CHENG Z Y, ZHU J Q, JIN Z. Study of surrogate model of endothermic hydrocarbon fuel RP-3[J]. Journal of Aerospace Power, 2016, 31(2), 391-398(in Chinese).
[13] DENG H W, ZHANG C B, XU G Q, et al. Visualization experiments of a specific fuel flow through quartz-glass tubes under both sub- and supercritical condtions[J]. Chinese Journal of Aeronautics, 2012, 25(3): 372-380.
[14] MAHDI M, MAJID B. The effect of the low Reynolds number k-e turbulence models on simulation of the enhanced and deterioration convective heat transfer to the supercritical fluid flows[J]. Heat Mass Transfer, 2011, 47(5): 609-619.
[15] HE S, KIM W S, BAE J H. Assessment of performance of turbulence models in predicting supercritical pressure heat transfer in a vertical tube[J]. International Journal of Heat and Mass Transfer, 2008, 51(19): 4659-4675.
[16] KIM W S, HE S, JACKSON J D. Assessment by comparison with DNS data of turbulence models used in simulations of mixed convection[J]. International Journal of Heat and Mass Transfer, 2008, 51(6): 1293-1312.
[17] LAUNDER B E, SHARMA B I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc[J]. Letters in Heat and Mass Transfer, 1974, 1(2): 131-137.
[18] ANSYS, Inc. Fluent 14.5 User Guide[M]. Lebanon: Fluent Inc., 2013.
[19] 张春本. 超临界压力下碳氢燃料的流动与换热特性研究[D].北京:北京航空航天大学, 2011.
ZHANG C B. Investigation of flow and heat transfer characteristics of hydrocarbon fuel at supercritical pressures[D].Beijing:Beihang University, 2011(in Chinese).
[20] WOOD R D, SMITH J M. Heat transfer in the critical region temperature and velocity profiles in turbulent flow[J]. AIChE Journal, 1964, 10(2): 180-186.
[21] BAE Y Y, KIM H Y, KANG D J. Forced and mixed convection heat transfer to supercritical CO2vertically flowing in a uniformly-heated circular tube[J]. Experimental Thermal Fluid Science, 2010, 34(8): 1295-1308.
[22] URBANO A, NASUTI F. On the onset of heat transfer deterioration in supercritical coolant flow channels: AIAA-2012-2880 [R]. Reston: AIAA, 2012.
程泽源男,博士研究生。主要研究方向:超临界流动换热。
Tel.:010-82339665
E-mail: cheng_zeyuan@buaa.edu.cn
朱剑琴女,博士,讲师,硕士生导师。主要研究方向:发动机热防护。
Tel.: 010-82339181
E-mail: zhujianqin@buaa.edu.cn
李海旺男,博士,副教授,博士生导师。主要研究方向:发动机热防护,微尺度传热及耦合布局。
Tel.: 010-82314379
E-mail: 09620@buaa.edu.cn
URL:www.cnki.net/kcms/detail/11.1929.V.20160223.0859.004.html
Diametereffectonheattransferdeteriorationofsupercriticalhydrocarbonfuelinverticalroundtubes
CHENGZeyuan,ZHUJianqin*,LIHaiwang
NationalKeyLaboratoryofScienceandTechnologyonAero-engineAero-thermodynamics,SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083,China
NumericalstudyofdiametereffectofheattransferdeteriorationofsupercriticalhydrocarbonfuelbyusingFluentwasconducted,LSlowReynoldsturbulencemodelwasusedforturbulencemodeling,andthephysicalpropertiesofsurrogatefuelofRP-3werecalculatedaccordingtoextendedcorrespondingstatelaw.Computationconditionsinthisstudyarelistedthesystempressureis3MPa,theinlettemperatureis573K,theheatfluxis500kW/m2andthemassflowsare0.0015,0.0030kg/s;theinnerdiameterrangesfrom1to10mm.Thecomputationmethodswereprovedtobeaccuratebygoodagreementbetweencomputedwalltemperaturesandexperimentalresultsundernormalheattransfer.Theresultsindicatethatinthecaseofforcedconvectionatlowmassflowtheheattransferdeteriorationoccursmoreseriouslyandinmoreforwardpositionwiththelargerdiameter;thereasonforheattransferdeteriorationisthatthespecificheatisinsharpdropregionafterthemaximumvalue,athighmassflowwalltemperatureisinpositiveproportiontotubediameterandthereisnoheattransferdeteriorationoccurring;thebuoyancyeffectworksonlyinlowmassfluxcasesandisenhancedwithlargerdiameter;thecriteriaofthebuoyancyeffectsworkingandtheheattransferdeteriorationboundarywithtubediametersaregiven.
supercritical;hydrocarbonfuel;heattransferdeterioration;diameter;buoyancy
2015-09-29;Revised2015-11-16;Accepted2016-01-30;Publishedonline2016-02-230859
s:NationalNaturalScienceFoundationofChina(51406005);DefenseIndustrialTechnologyDevelopmentProgram(B2120132006)
.Tel.:010-82339181E-mailzhujianqinbuaa@sina.com
2015-09-29;退修日期2015-11-16;录用日期2016-01-30; < class="emphasis_bold">网络出版时间
时间:2016-02-230859
www.cnki.net/kcms/detail/11.1929.V.20160223.0859.004.html
国家自然科学基金 (51406005); 国防基础科研项目 (B2120132006)
.Tel.:010-82339181E-mailzhujianqinbuaa@sina.com
程泽源, 朱剑琴, 李海旺.竖直圆管内超临界碳氢燃料换热恶化的直径效应J.航空学报,2016,37(10):2941-2951.CHENGZY,ZHUJQ,LIHW.DiametereffectonheattransferdeteriorationofsupercriticalhydrocarbonfuelinverticalroundtubesJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):2941-2951.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0037
V312+.1
A
1000-6893(2016)10-2941-11
