课例研究漫谈——教学关注思维层次的启发
2016-11-19江苏省南通市通州区金沙中学季汉杰
☉江苏省南通市通州区金沙中学季汉杰
课例研究漫谈——教学关注思维层次的启发
☉江苏省南通市通州区金沙中学季汉杰
数学课堂教学是学生学习数学的主阵地,是启发学生对数学知识进行理解、记忆、反思、运用的场所.课程标准指出:“数学教学要致力于对学生思维的启发和培养,将学生的学习从被动接受转变为主动探索.”课程标准的想法非常美好,但是可以这么说,真正在常态课教学中能做到以启发思维为主的教学设计少之又少.
大量调查资料显示,这一教学理念实施非常困难的原因在于:第一,我们教育的现状是以教师引导下的启发式为主的教学,以高效课堂为主的教学模式势必强调了灌输,从而让自主思维愈来愈僵化;第二,课程改革和高考改革步调并不一致,课程改革强调自主探索、积极建构,这一方式耗时耗力,势必延缓教学进度,而高考内容和难度却一再加深,若长时探索必定浪费时间,造成应试能力的下降.因此,笔者认为,可以在不同的课程类型中使用不同的教学方式,要提高思维层次性,还是要从合理的教学设计入手,螺旋式上升的进行.
一、课例设计
课例绝对值不等式应用案例设计.
思维设计一:已知函数f(x)=|x-a|,g(x)=f(x)+f(x-1).
(1)若不等式f(x)≤2的解集为{x|-1≤x≤3},求实数a的值.
思维分析:从绝对值最简捷的相关不等式出发,复习回顾初中数学相关的简单绝对值不等式的解决方法,并将不等式与方程进行有机结合.这里的思维设计属于第一层次,即基本知识的回顾和整理.
解析:由f(x)≤2,得|x-a|≤2,解得a-2≤x≤a+2.又不等式f(x)≤2的解集为{x|-1≤x≤3},所以解得a=1.
归纳:|ax+b|≤c,|ax+b|≥c(c≥0)型不等式的解法.
方法一:①若c>0,则|ax+b|≤c等价于-c≤ax+b≤c,|ax+b|≥c等价于ax+b≥c或ax+b≤-c,然后根据a,b的值解出即可;②若c<0,则|ax+b|≤c的解集为Ø,|ax+b|≥c的解集为R.
方法二:不等式两边平方去掉绝对值符号即可.
思维设计二:在(1)的条件下,若对一切的实数x恒有g(x)≥m,求实数m的取值范围.
思维分析:关注基本问题的发散,教师给出了中学数学恒成立相关基本问题,请学生思考恒成立问题的基本处理方式.当a=1时,g(x)=|x-1|+|x-2|,若对一切的实数x恒有g(x)≥m等价于m≤g(x)min.这里进行的思维设计属于第二层次,在思维最直接解决不等式问题的基础上,开发了绝对值恒成立的设计,对于该问题所具备的思维,即在基本思维储备的基础上螺旋式上升地提高了知识的运用能力.
解法一:当a=1时,g(x)=|x-1|+|x-2|,于是g(x)=|x-当x>2时,g(x)>1;当1≤x≤2时,g(x)=1;当x<1时,g(x)>1.综上,对任意的实数x,g(x)min= 1,所以m≤1.
解法二:当a=1时,g(x)=|x-1|+|x-2|,由|x-1|+|x-2|≥|(x-1)-(x-2)|=1,当且仅且当(x-1)(x-2)≤0,即1≤x≤2时等号成立,故对任意的实数x,g(x)min=1,所以m≤1.
说明:①研究含有绝对值的函数问题时,根据绝对值的定义,分类讨论去掉绝对值符号,转化为分段函数,然后数形结合解决是常用的思维方法;②对于求f(x)=|x-a|+|x-b|或f(x)=|x-a|-|x-b|型的最值问题利用绝对值三角不等式更方便.形如f(x)=|x-a|+|x-b|的函数只有最小值,形如f(x)=|x-a|-|x-b|的函数既有最大值又有最小值.这里的解决方式体现了思维设计的两个方向,第一种方式从分类讨论的角度切入,旨在培养学生分类讨论的数学思想;第二种方式更是从数学概念、绝对值本质的角度入手思考(即三角不等式的使用),让问题的解答颇有“山重水复疑无路,柳暗花明又一村”的感觉!
思维设计三:在(1)的条件下,对任意实数b(b≠0)和c,不等式|b|g(x)≤|b+c|+|b-c|恒成立,求实数x的取值范围.
思维分析:启迪学生思维,教师在问题设计的时候需要关注一些数学小技巧的处理,此处将恒成立问题进行了深化,将参变分离的思想引入进来,在思维设计二的基础上进一步提高了不等式恒成立问题解决的思维层次性,实现了设计的层层递进和思维的循序渐进.当a=1时,g(x)=|x-1|+|x-2|,不等式等价于g(x)≤恒成立,即,即|x-1|+in.因为|b+c|+|b-c|≥|(b+c)+(b-c)|=2|b|,当且仅当(b+c)(bc)≥0时等号成立,所以|x-1|+|x-2|≤
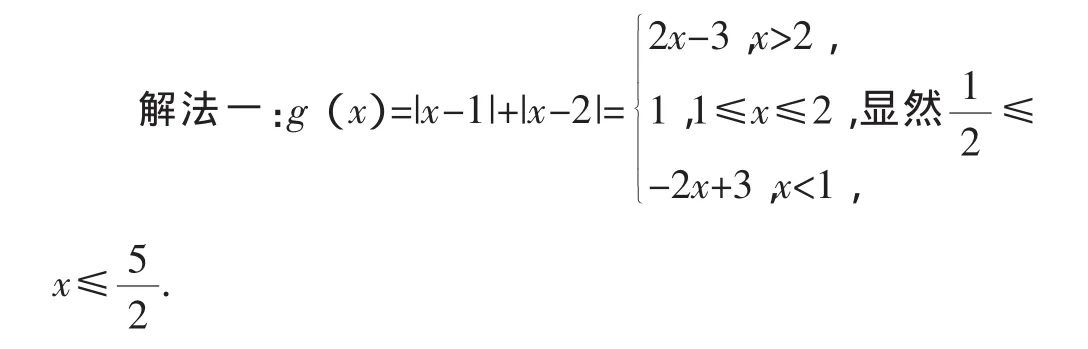
解法二:如图1,设数轴上与1,2对应的点分别是A,B,则不等式的解就是数轴上到A、B两点的距离之和小于等于2的点所对应的实数.显然,区间[1,2]满足不等式的解集.把A向左移动一个单位到点A1,此时|A1A|+|A1B|=0.5+1.5=2.把点B向右移动一个单位到点B1,此时|B1A|+|B1B|=2,故原不等式的解集为
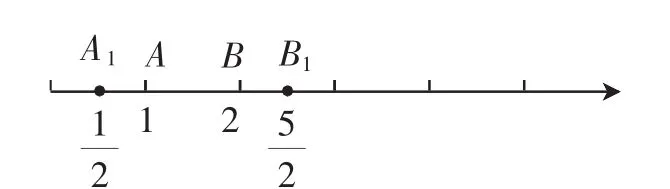
图1
解法三:如图2所示,利用数形结合思想即可.
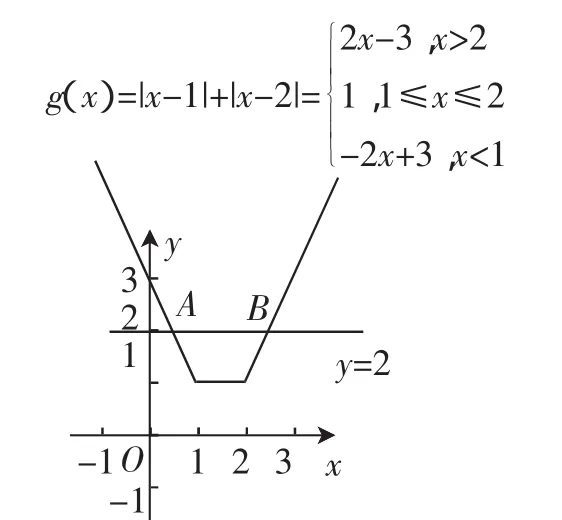
图2
说明:形如|x-a|+|x-b|≥c(或≤c)型的不等式主要有三种解法:①分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为((-∞,a],(a,b],(b,+∞),此处设a
二、设计反思
回顾上述教学设计,我们看到了教师在引导、启发学生思维方面做出的三个不同思维设计,这样的设计符合了层次性原则:
(1)思维设计一是教师教学必须做的基本思维启发,这种启发更多的是依赖于知识的回顾,暗示本课所要达到的方向,这种设计尽管较为平淡,也是数学教学最无可厚非的形式化展示.
(2)思维设计二是结合恒成立进行的问题的处理,我们知道恒成立问题对于初学者而言往往是思维混淆的,这里笔者常常借助于一个形象的年龄比喻:将班级某学生甲和某幼儿园所有学生的年龄比大小,我们只要找到甲比该幼儿园中年龄最大的幼儿大即可,即大于最大值;将班级某学生甲和某大学所有学生的年龄比大小,我们只要找到甲比该大学中年龄最小的大学生小即可,即小于最小值.笔者认为,这种思维的形象化启发是有助于利用非形式化手段阐述形式化的数学过程和结论的,即在学生抽象理解的层面上做到了非常独到的思维启发.
(3)思维设计三是恒成立问题的进一步处理,这里笔者想要做的是进一步的思考启发,即恒成立问题在混乱状态下的清晰分离.从处理方式来说,参变分离是首选的方法,即将问题转换为上述年龄问题的理论,这是最好的解决状态.另外,考虑到绝对值不等式相关的问题还有更为简捷的距离本质(几何意义),教师也从这一角度进行了多解性的思考和引导,进一步加深了学生在知识多角度上的思维启发,可以这么说教师在该节的设计处在了层层递进的思维上,是较好的思想型课堂.
任何教学设计都存在着一定不足性,笔者课后反思了本课注重思维启发的设计环节,产生了一些可以继续优化的教学环节:首先,课堂引入环节的思维设计显得与后续知识衔接性不足,在指向性上存在着不足,若教师能将后续知识在这里进行基本环节的铺垫,能更好地体现思维设计一的重要性;其次,绝对值不等式相关的问题类型比较多,这里对于两种思想方法,即分类讨论思想和数形结合思想引入较为到位,但是恒成立问题的设计显得有些单一,若能更为开放地选择一些试题,那么既在问题的多样性上有了实践探索,又在思维上做到了一定的启发,这样的思维设计显得更为丰满一些.
总之,现阶段教学不能总是以解题重复训练为主基调,更要从思维训练的角度进行教学设计,只有关注思维的培养才能将学生的数学素养和能力进行提升,否则,数学学习对于学生而言永远是一种重复的机械训练,不利于其思维能力的培养.因此,课堂教学中教师多多关注思维层次性的教学是提高自身课堂教学水平和学生学习能力的关键.
1.杨建辉.新课程标准下教师教学设计中应具备的几种意识[J].数学通报,2014(2).
2.冷少华.浅谈学生的数学问题意识及其培养[J].教育探索,2013(6).
