从思想视角入手课堂教学设计
2016-11-19江苏省南通市通州区金沙曹卫民
☉江苏省南通市通州区金沙曹卫民
从思想视角入手课堂教学设计
☉江苏省南通市通州区金沙曹卫民
课堂教师设计考验的是教师的综合能力,这不仅是对基本知识传授顺序性、合理性等的思考,还需要考虑在传承知识的同时,在思想方法等角度是否给予学生有足够的启发.笔者近期从一堂公开课设计的思想视角谈一谈,如何在尊崇学生学情基础上,结合知识与思想进行的教学设计,请读者批评指正.
一、设计准备
1.最近知识发展区
在这节课时之前,学生已经学习了一元二次不等式的简单解法以及运用二次不等式与二次函数、二次方程的关系解决实际运用问题.对于三个“二次”之间的转化和数形结合已经有了一定的体会,这将有助于学生在本节课学习中利用分类讨论、数形结合、化归等数学思想综合处理问题.
2.学生能力储备
学生在初中学习中对一元一次不等式组、二次函数的图像以及二次方程已经有了深刻的学习,但对于一元二次不等式与图像及方程综合结合解题的方法和思想不是很熟练.前两节课已经学会利用图像解二次不等式以及简单含参问题的分类讨论有所了解.但是对于含有多个变量的不等问题的处理的能力还是不足,不会对其题意进行转化、不会利用数形结合思想综合分析.
二、策略分析
通过以上对本节教学内容的重难点、学生学情的分析,以及所要达成的学习目标,特对本节课的教学作如下安排:
(1)以简单含参二次不等式的具体实例进行引入,加深学生利用函数图像解二次不等式的解法理解,同时引导学生对参数的分类讨论、利用数形结合思想解题;
(2)根据学生的认知规律,通过对变式及思考,将解不等式问题层层深入、梯级拓展,进而对二次不等式的恒成立问题的化归思想的应用、利用数形结合解题、变参分离的处理方式、主次变量的正确选取等方法有一定的了解.
三、过程设计
1.旧题新做,引入主题
解关于x的不等式x2+(a-4)x+4-2a<0.
师:该二次不等式是含有参数a的不等式,可因式分解为(x-2)[x-(2-a)]<0,根据二次不等式的解法,两根x1=2,x2=2-a的大小未定,讨论根的大小,进而解不等式.
解析:当2>2-a,即a>0时,2-a<x<2;当a=0时,x≠2;当2<2-a,即a<0时,2 设计思路:设计问题主要是刺激学生回忆自己已有的知识和技能,回忆起含参二次不等式的解法,有意识地使学生和函数图像紧密结合解题的习惯,另外是对不等式中参数a的重要作用重视. 2.拓展探究,层层上升 预设:如何将本题题意进行等价转化可能是学生思维上的不足,如何引导学生做正确的等价转化,这里需做好合理的引导. 师:根据题目文字叙述你可等价转化为什么数学条件?并能总结出哪些数学关系式?(学生单独回答) 师:该题函数的简单综合,以幂函数为模型实质为二次函数特征.利用幂函数的定义域被开方数大于等于0,转化为x2+(a-4)x+4-2a≥0. 解析:由题意等价为x2+(a-4)x+4-2a≥0在R上恒成立,则Δ=(a-4)2-4(4-2a)≤0,解得a=0. 设计思路:该题以基本初等函数的基本性质和二次函数的图像特征为知识基础,培养学生解决函数综合问题的能力,会利用化归思想解题. 变式2二次函数f(x)=x2+(a-4)x+4-2a,若不等式f(x)<0的解集为A,又B={x|1<x<3},若A⊆B,求实数a的取值范围. 预设:在这题的学生可能会先从解出集合A入手,进而再利用集合的包含关系求a,学生很容易遗忘空集是任意集合的子集,教师应提醒学生注意思维的缜密性,并在此基础上引导学生利用二次函数图像数形结合直接解题. 师:根据题意你们会直接解出利用A,再利用A包含于集合B解题. 这里解不等式的过程可以省略,参照例1. 师:函数为二次函数,根据前面内容我们可作出二次函数图像,我们如果利用函数图像该怎么解本题? 生:作图思考. 师:根据我们已作出的此二次函数图像,且函数f(x)=(x-2)(x-2+a)=0的两根x1=2,x2=2-a,只需方程的根在区间(1,3)内即可,转化为二次方程根的分布.但注意空集这种特殊情况. 解析:二次函数开口向上,利用二次函数函数的图像特征,只需方程f(x)=0的根均在区间(1,3)内,则①A= Ø,则a=0;②A≠Ø,则2∈(1,3),所以2-a∈[1,3],则a∈[-1,0)∪(0,1].综上所得a∈[-1,1]. 设计思路:设计本题的目的是让学生不仅可以在常规情况下解决含参不等式,更主要是诱导学生正确利用函数图像、数形结合思想在解题中的运用.重点是引导学生,让学生体会数形结合解题的美妙与直观,进而养成数形结合的习惯. 变式3方程(log4x)2+alog4x+4-2a=0在[16,+∞)上有两不等实根,求a的取值范围. 预设:学生对一元二次方程根的分布有一定的了解,但对于与其他函数结合,利用换元思想可能还不是很熟练,特别是对数函数是学生的薄弱之处,如何启发学生将对数换元进而转变成他们熟悉的二次方程,另外学生换元之后新元素的范围不一定会考虑到. 师:关于x的方程可用换元的思想将log4x=t,则方程就等价为t2+at+4-2a=0在t∈[2,+∞)有不同两解,转化为二次方程根的分布的基本题型. 解析:设log4x=t,因为x≥16⇒t≥2,所以等价于方程t2+at+4-2a=0有两个大于等于2的不等实根,则需满足 设计思路:该题是二次不等式与其他知识的融汇整合,如何将学生不熟悉的问题转化为熟悉的问题,使他们遇到问题做好等价转化,利用换元等方法将题型基本化,使问题简单化. 课后思考:将条件改为log4x改为2x,将区间改变又如何呢? 变式4对于任意α∈[-π,π],不等式cos2α+(4-a)· sinα+2a-5<0恒成立,求a的取值范围. 预设:学生看到这个题干可能被其复杂形式所吓倒,但在变式3的基础之上,可以提示学生该题是不是也可将题意转化为简单形式.有些学生可能对于题目中多个变量无所适从,明确题目中自变量与参数的正确选择也是解题的关键.另外这题的解题方法也相对比较灵活,也是本节课的重点难点所在,所以可以进行小组活动,进而激发每个人的参与度. 师:将学生进行分组活动,根据学生能力可将学生四人作为一个小组,一起解决这个问题,可以让学生让学生带着问题进行小组活动.问题1:利用换元法解该题选择sinα还是cosα更好?问题2:若换元后转化为什么样的问题?并能如何解决.问题3:化归解决此类问题的思路是什么? 可给学生5分钟左右时间,在此过程中教师可参与每个组,发现每个组的思维漏洞或者方法. 学生成果展示,教师进行点评归纳. 师:根据上题思想可先换元,将cosα=x,α∈[-π,π],则x∈[-1,1],原题就等价于对于任意x∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,求a的取值范围.那接下去应该如何解决该恒成立问题? 师:含参恒成立问题是高中数学的一个难点,也是本节课的重难点.该题为恒成立问题,是关于x的二次不等式,求参数a的范围.一般可以转化为二次函数并利用二次函数的性质进而转化为求函数最值或者变参分离为a>f(x)max或a<f(x)min解题. 分析:先换元,令cosα=x,α∈[-π,π],则x∈[-1,1],原题就等价于对于任意x∈[-1,1],不等式x2+(a-4)x+ 4-2a>0恒成立,求a的取值范围. 解法一(利用函数性质,转化为最值求解):可令函数f(x)=x2+(a-4)x+4-2a,题意等价于f(x)min>0,x∈[-1,1]. 综上所得a<1. 解法二(利用二次函数图像特点及二次方程根的分布):函数f(x)=x2+(a-4)x+4-2a=(x-2)(x+a-2)的两根为2和2-a,因为二次函数图像开口向上,所以只需f(x)<0的解集为[-1,1]交集为空即可,则x2=2-a>1,即a<1. 解法三(参变分离):x2+(a-4)x+4-2a>0⇒a(2-x)<x2-4x+4,因为x∈[-1,1],则2-x>0,则易得2-x的最小值为1,所以a<1. 课后思考:将变式4中一次项改为5-2a,或者将x范围变成(1,3),求a的取值范围. 师:(方法小结)解决恒成立问题的方法一般有两种:第一构造函数,转化为函数最大值大于零或最小值小于零,利用函数性质,转化为最值问题解题;第二变参分离,弄清主次变量转化为a>f(x)max或a<f(x)min再利用函数最值解题.但两种方法殊途同归,最后就是求函数的最值. 设计思路:本题是本节课的重难点,含参的二次不等式恒成立问题,也是常见的不等式恒成立问题.通过本题的学习让学生了解解决恒成立问题的常规方法和思维方式. 本节课的基本设计是对同一题面的多种变式,达到对不等式恒成立问题的常用方法的介绍、换元化归思想的运用、数形结合解题的体会的教学目的.根据学生的认知规律,变式探究,层层递进,螺旋上升,体现了新课程理念.对于重难点的处理,主要是采用了先由学生进行自主、合作学习,再通过展示、交流、深入、归纳出知识的学习过程,调动了学生的积极性,激发每个学生的思维潜能,感受知识的获得过程,这比教师单纯的教授方法要更有印象更有启发,也更能培养学生发现问题、研究问题的能力与习惯.在教学过程中,精心做好每一个变式,有变化有梯度,内容丰富,同时也十分关注课堂生成,在数学学习的过程中,特别注重对数学思想方法的应用,对数学本质的理解. 1.吴志雄.培养高中生数学应用意识的策略与思考[J].中学数学研究,2013(11). 2.刘见乐.用思想方法指导高中数学教学[J].中国数学教育,2014(5). 3.周强.高中数学教学设计中思想渗透分析及对策研究[J].数学教学通讯,2014(9).
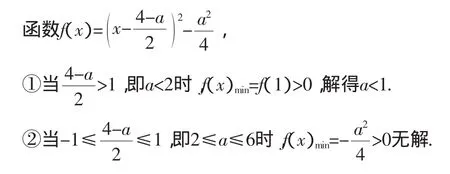
四、一点思考
