基于自适应模糊的自平衡车行走控制

陈静，李冰，李莉，李宗帅

（1.天津职业技术师范大学信息技术工程学院，天津300222；2.中国民航大学航空自动化学院，天津300300）

基于自适应模糊的自平衡车行走控制

陈静1，李冰1，李莉1，李宗帅2

（1.天津职业技术师范大学信息技术工程学院，天津300222；2.中国民航大学航空自动化学院，天津300300）

针对两轮自平衡车的行走控制问题，在考虑地面摩擦的前提下，采用拉格朗日建模方法，建立了两轮自平衡车的多输入多输出非线性系统模型，采用自适应模糊方法在所建立模型的基础上，研究了自平衡车的行走控制。本文所提方法在自适应模糊控制部分仅需反馈机器人的倾角和倾角速度便可实现机器人的前进控制，轨迹控制部分通过给定期望的轮速差并通过PID控制器反馈到输入来实现。仿真实验表明：该方案可以控制自平衡车以一定的速度前进和转弯，进而实现自平衡车不同行为的控制。

两轮自平衡车；拉格朗日建模；自适应模糊控制；行走控制

众所周知，Segway是一种自动平衡行人辅助工具，相似的机器人实体还有轮式倒立摆、自平衡轮椅、JOE、nBot等［1-4］，这些机器人实体都具有自我平衡并向前行驶的功能，这一功能需要相应的控制算法来实现［5］。在建模过程中，有些文献并没有考虑地面摩擦的作用［3］，而这一点是不能忽略的。由于摩擦的作用，系统的稳定运行状态速度和姿态角度具有一定关系，可以通过控制倾角大小来控制机器人的行走速度。在控制方法上，机器人的平衡控制算法有多种，包括传统的PID控制方法、陈星等［6］采用具有圆盘极点和反差约束的鲁棒控制算法设计的状态反馈控制律等。采用PID控制方法，需要反馈倾角积分项才能实现倾角的跟踪，但PID参数需要根据经验调节，如果系统参数变化，控制参数需要重新调节，不是一种智能的控制方法［4-7］。而自适应控制能够很好地实现系统跟踪［8］。本文考虑了地面摩擦的作用，建立了两轮自平衡系统的数学模型，并采用一种自适应的控制方法，通过仅反馈倾角和倾角速度来实现倾角的跟踪控制，具有较好的控制效果，可以实现两轮自平衡车的平衡行走控制。

1　人体平衡的基本原理

肢体在水平面上的直立运动由2个外部因素决定：作用于质心（center of mass，COM）上的重力mCOMg和作用在压力中心（center of pressure，COP）上的地面反作用力fCOP，肢体平衡原理如图1所示。

图1　肢体平衡原理图

根据人体平衡的力学条件，合力为零，合力矩为零，即：∑F=0、∑M0（F）=0，可得到

式中：mCOM为肢体总质量；ICOM为转动惯量；fH和fV分别为反作用力fCOP水平方向和竖直方向上的分量；τ为踝部肌肉提供的转矩；v和ω分别为质心的速度和角速度；D为相对于转轴的距离。由此得到肢体的数学模型为：

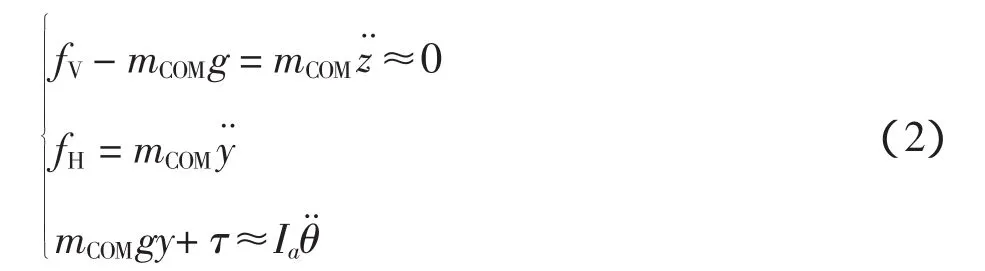
式中：y和z分别为重心相对于踝关节位置的水平分量和竖直分量。

直线倒立摆系统如图2所示。倒立摆系统是模拟图1肢体平衡原理的机械系统，但该系统只适用于研究静态平衡问题。由于导轨长度的限制，对于行走平衡问题，采用倒立摆系统并不合适。为脱离倒立摆导轨的限制，将肢体平衡原理移植到轮式移动机器人当中，自平衡机器人的概念应运而生。自平衡机器人是一种模拟人体平衡原理的智能系统，而应用该系统的电动车已在国内外市场上普及，成为未来潜在的交通工具。其主要的平衡原理是采用陀螺仪和加速度传感器组成的惯性组件，自动测量人体重心的微小变化，从而保持平衡并控制运动方向。性能良好的运动平衡控制算法对该类产品的安全稳定运行起到了关键作用，控制方式的研究对运行功能的拓展也起到了推动作用。

图2　直线倒立摆系统示意图

2　两轮自平衡电动车系统

2.1系统介绍

两轮自平衡电动车系统，从硬件结构上主要包含组织级、协调级和执行级3个模块，如图3所示。

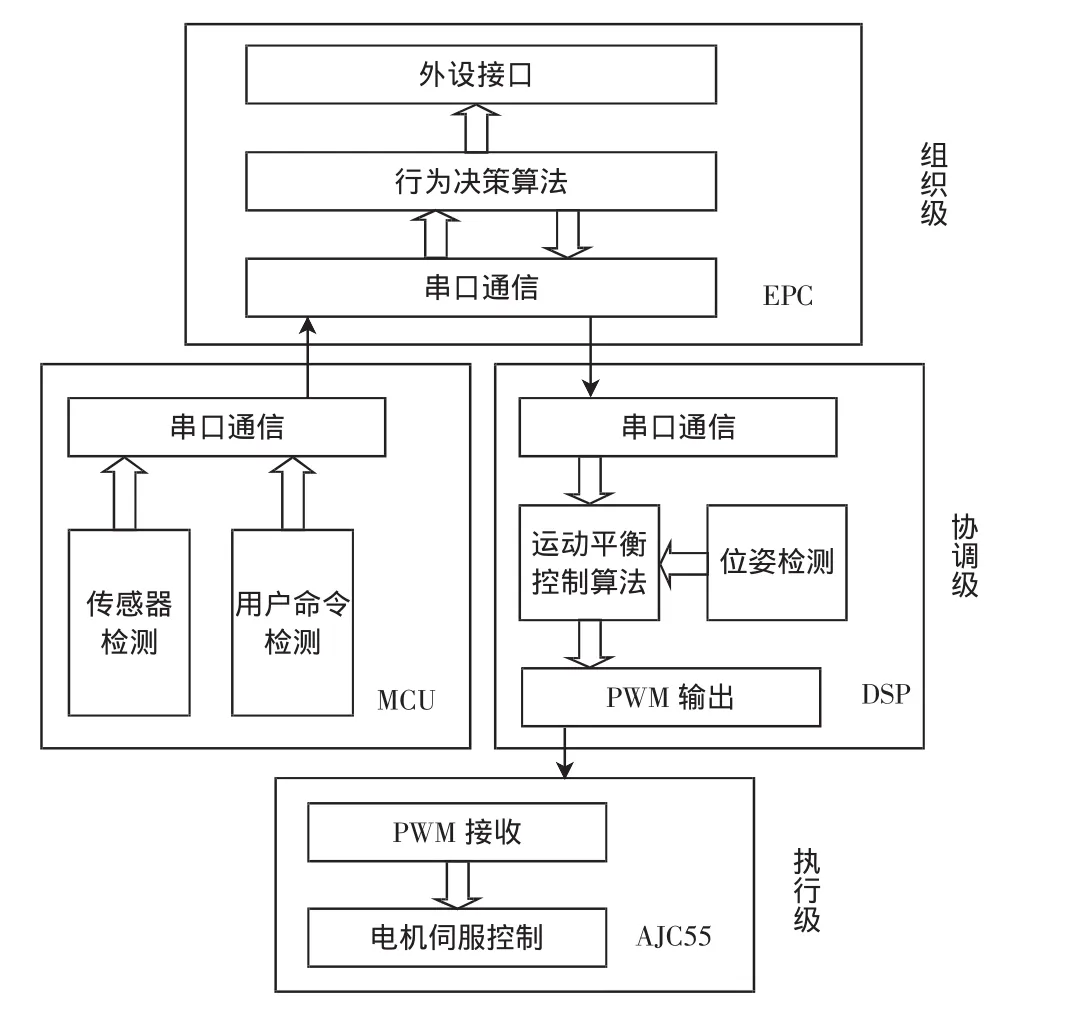
图3　自平衡车系统硬件结构图

图3中，控制部分主要由协调级和执行级完成。协调级主要包含传感器和命令的检查回传及运动平衡控制算法的控制中枢；执行级主要为电机的伺服控制。

2.2系统模型

2.2.1动力学模型

用Lagrange方法推导系统的动力学方程，Lagrange算子为：

式中：L为拉格朗日算子；T为系统的总动能；V为系统的总势能，则拉格朗日方程为：

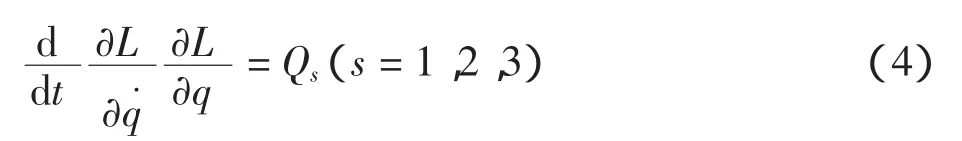
式中：q为系统的广义坐标，定义q=（α，φl，φr）T，分别为自平衡车倾角和两个轮子的转角。

Q1=τd-τl-τr；Q2=τl-μlRsign（φ˙l）（φ˙l）2；Q3=τrμlRsign（φ˙r）（φ˙r）2，τd为给自平衡车上体的扰动，τl和τr为左右电机提供的转矩，Q2和Q3为左右轮克服摩擦后的左右轮合力矩，这个摩擦的方向应该与运动方向相反，大小与转速平方成正比。根据选用电机的不同，所输出的最大转矩也不同，这里限定幅值为±5 N·m。

系统总动能：包括平动动能和转动动能之和。

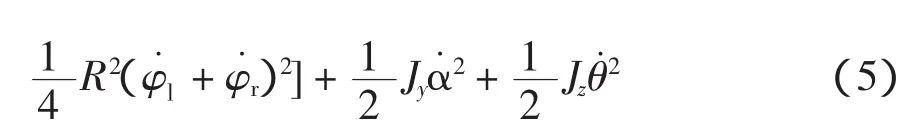
式中：θ˙=R（φ˙l+φ˙r）/L为偏航角速度。

系统总势能为：

将式（4）和式（5）代入式（3），整理得自平衡车多输入多输出非线性系统模型为：

写成矩阵方程形式为：

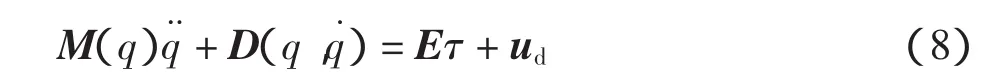
其中：

根据欠驱动系统的定义，对于具有仿射非线性形式q¨=f1（q，q˙，t）+f2（q，q˙，t）u的系统，如果满足rank［f2（q，q˙，t）］＜dim［q］，即不能在q的任意一个方向上给一个瞬时加速度，称这个系统为欠驱动系统。对于自平衡车来说，rank（E）=2＜3，因此该系统为欠驱动系统。

2.2.2运动学模型

自平衡车的运动学模型可描述为：

2.2.3模型分析

研究表明，当自平衡车处于某一稳态情况下，系统满足如下等式：

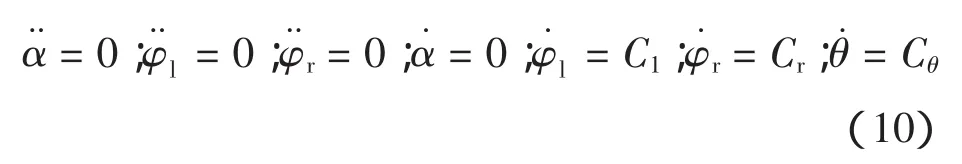
将式（10）代入非线性系统模型（7），可以推导出轮速和倾角的关系为：

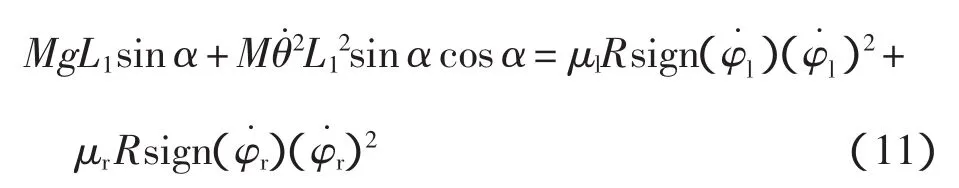
在直线行走和低速运行条件下，Mθ˙2L12sin α cos α同MgL1sinα相比是可以忽略的。因此，在稳态行走情况下，倾角和速度有如下关系：

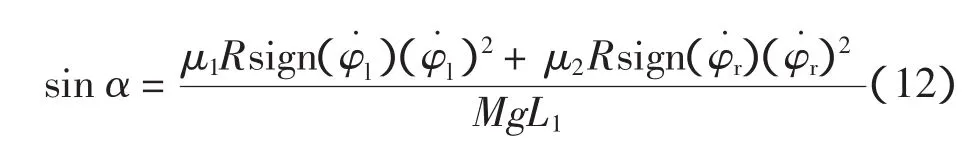
直线行走情况下：

式中：v为前进速度。拟合速度和倾角的关系如图4所示，图4（a）为左、右轮速度同倾角的关系，图4（b）为直线运行情况下前进速度同倾角的关系。

图4　速度与倾角关系拟合曲线图

通过式（12）和式（13）可以看出，两轮角速度和倾角的关系与轮子和地面的摩擦系数有关，在摩擦系数一定且系统匀速运动的稳态下，速度越大，倾角越大。利用这一关系，速度的控制可转化为倾角的控制，即通过控制倾角来控制速度。由于电机所能提供的转矩有限制，因此自平衡车所能控制的倾角和身体所能承受的外界冲击力是有限的，超过该限制后，自平衡车就会倾倒，这是本身硬件条件决定的。因此，自平衡车所能控制的倾角范围是一定的。

第一个界限是所能控制倾角的界限。经过反复仿真验证，0.257 95 rad是所能控制倾角的界限，此时角度为14.779 4°，即自平衡车可以以一定的速度向前运行，并保持这个倾角不变。第二个界限是可控制平衡的最大初始角度。经反复仿真验证，对于本文所设计的硬件系统来说，这个界限为0.442 13 rad=25.332 2°，即如果初始角度大于这个范围，电机没有足够的动力使其平衡。初始状态为［q，q˙］=［0.44213 0 0 0 0 0］时的控制结果如图5所示。

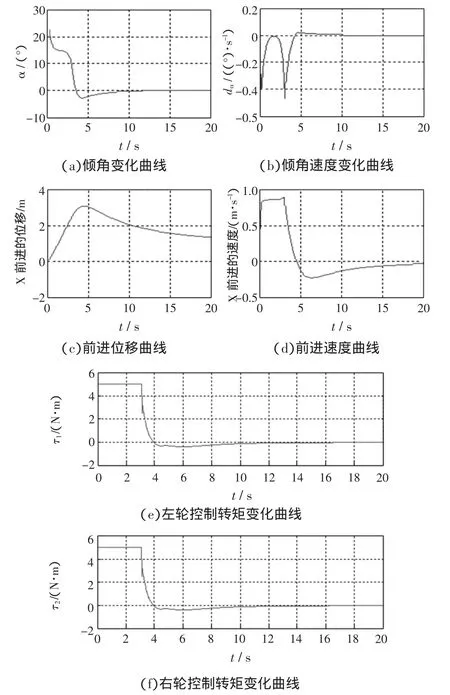
图5　初始状态为［0.44213 0 0 0 0 0］的平衡控制结果图

3　基于模糊自适应的运动控制器的设计

3.1自适应模糊控制

自适应模糊方法可以实现非线性系统的跟踪控制，同普通PID控制方法相比，该控制方式对参数具有一定的鲁棒性，且对模型的精确性没有依赖。

在之前的研究中，采用自适应模糊控制方法实现了两轮自平衡机器人的平衡控制，详见参考文献［9］。

经过李雅普诺夫稳定性证明，参数的自适应律为：

式中：γ为正常数；pn为P的最后一行；P为一个正定矩阵且满足方程ATP+PA=-Q；Q为任意的一个n×n

k2，…k，选择合适的K使多项式s（n）+kns（n-1）+…+k1=0的根在平面坐标系的左半平面。

3.2匀速直线运动控制器的设计

控制任务是使自平衡车以0.3 m/s的速度前行，即轮子转动角速度为2 rad/s。由上文中对模型的分析可求出对应的倾角，为0.030 6 rad。在MATLAB7.1中进行Simulink仿真，如图6所示。

图6　Simulink控制结构图

twrctrol部分采用自适应模糊控制方法，该控制方法能够实现非线性系统的跟踪控制，且对模型的精确性没有较高要求。模型在转化为式（11）时，其中的g（x）＜0，因此参数的自适应律为θ˙=-rξ（x）pne。当直线行走时，期望轮速差=0，期望倾角=0.030 6 rad=1.753 3°，期望倾角速度=0，控制结果如图7所示。

图7　直线行走控制结果图

3.3旋转行走控制

由图6可知，将期望的轮速差和实际的轮速差比较，并采用PID控制方法反馈到电机的转矩控制中，可以实现机器人的旋转控制。当旋转行走时，期望左轮角速度为2 rad/s，右轮角速度为1 rad/s，期望轮速差=1 rad/s，期望倾角=0.019 1 rad=1.096 3°，期望倾角速度=0，控制结果如图8所示。

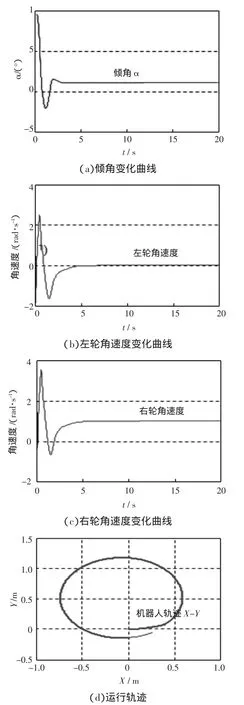
图8　旋转行走控制结果图

4　结束语

本文分析了两轮自平衡车的行走控制，采用自适应模糊控制方法，仅反馈倾角和倾角速度便可实现机器人的平衡控制和匀速行走控制。在此基础上，通过增加两轮速度差与期望速度差的PID反馈控制，实现机器人的转弯控制。仿真实验表明：采用这一控制方案，可以有效解决自平衡车的行走平衡问题。

［1］PATHAK K，FRANCH J，AGRAWAL S K.Velocity andposition control of a wheeled inverted pendulum by partial feedback linearization［J］.IEEE Transactions on Robotics，2005，21（3）：505-513.

［2］BLANKESPOOR A，ROEMER R.Experimental verification of the dynamic model for a quarter size self-balancing wheelchair［C］//American Control Conference，2004.Boston：IEEE，2004：488-492.

［3］CHAN R P M，STOL K A，HALKYARD C R.Review of modelling and control of two-wheeled robots［J］.Annual Reviews in Control，2013，37（1）：89-103.

［4］杨正才，吕科.基于模糊PD控制方法的两轮直立自平衡电动车研究［J］.控制工程，2016，23（3）：366-370.

［5］姜立标，何家寿.两轮自平衡代步车控制策略及动力学仿真［J］.华南理工大学学报：自然科学版，2016（1）：9-15.

［6］陈星，魏衡华，张玉斌.二轮行走倒立摆系统建模与鲁棒方差控制［J］.计算机仿真，2006，23（3）：263-266.

［7］刘二林，姜香菊.基于PID算法的两轮自平衡车直立控制［J］.自动化与仪器仪表，2015（2）：203-206.

［8］WUTS，KARKOUBM，WENGCC，etal.Trajectory tracking for uncertainty time delayed-state self-balancing train vehicles using observer-based adaptive fuzzy control［J］. Information Sciences，2015，324：1-22.

［9］RUAN X G，CHEN J，CAI J X，et al.Balancing control of two-wheeled upstanding robot using adaptive fuzzy control method［C］//2009IEEEInternationalConferenceonIntelligent Computing and Intelligent Systems.Shanghai：IEEE，2009：98-101.

Walking control of two-wheeled self-balancing vehicle based on adaptive fuzzy

CHEN Jing1，LI Bing1，LI Li1，LI Zong-shuai2
（1.School of Information Technology Engineering，Tianjin University of Technology and Education，Tianjin 300222，China；2.School of Aeronautics and Automation，Civil Aviation University of China，Tianjin 300300，China）

For the walking control problem of two-wheeled self-balancing vehicle，the nonlinear MIMO model of twowheeled self-balancing vehicle considering the friction of ground has been built based on Lagrange method.Using adaptive fuzzy method the walking control for two-wheeled self-balancing vehicle is researched based on the built system model. With the feedback of inclination angle and inclination angle velocity，the walking control would be realized in the part of adaptive fuzzy control using the proposed method in this paper.In addition，tracking control in level can be achieved by PID controller with the error between expected and actual velocity error of two-wheels，which will be feedback to the input of system.The simulation results show that the proposed scheme in this paper can make robot walking forward and turning with a certain speed，and then different behavior for self-balancing vehicle can be realized.

two-wheeled self-balancing vehicle；Lagrange modeling；adaptive fuzzy control；walking control

TP242

A

2095－0926（2016）03－0024－06

2016-05-09

国家自然科学基金青年项目（61403282）；天津市高等学校科技发展基金计划项目（20130807）；天津职业技术师范大学科研启动项目（KYQD13004）；天津职业技术师范大学科研发展基金项目（KJY1311）.

陈静（1984—），女，讲师，博士，研究方向为智能控制、机器人及认知学习等.