非线性规划约束问题求解方法及其应用

2016-11-18刘兆鹏费时龙

绥化学院学报 2016年11期

关键词：运筹学宿州乘数

李　杰　刘兆鹏　费时龙　苏　婷

（宿州学院数学与统计学院　安徽宿州　234000）

非线性规划约束问题求解方法及其应用

李杰刘兆鹏费时龙苏婷

（宿州学院数学与统计学院安徽宿州234000）

非线性规划于20世纪50年代形成，近几十年里迅速发展，已经在经济、军事及工程等领域有着广泛的应用。文章一方面，简要介绍了非线性规划的概念及非线性规划的模型相关概念；另一方面，研究了非线性规划约束极值问题常见的求解方法Lagrange乘数法与可行方向法具体的运算方法与步骤，并通过具体的实例阐述论证。

非线性规划；模型；方法；极值

一、非线性规划的数学模型

如果目标函数[1]或者约束条件中含有非线性函数则称为非线性规划问题，非线性规划的数学模型[2]如下：

其中：x=(x1,x2,x3,……xn）是一个n维向量。

由于hk(x)=0等价于：

若把可行解区域[3]记为：Ω={x|gi(x)≥0,i=1,2,……m}则非线性规划[4]问题又简记为：minz=f(x),x∈Ω

Ω={x|gi(x)≥0,i=1,2,……m}与z=f(x)分别为非线性规划问题的可行解集和目标函数。非线性规划约束极值问题的一般定义为：

函数f(x)或g(x)至少有一个非线性的，f(x)与g(x)是连续且可微函数。

二、非线性规划约束极值求解方法及其应用

（一）Lagrange乘数法。当z=f(x,y)与φ(x，y)都可微，且φy(x0，y0)≠0知：在(x0,y0)处，φ(x，y)=0确定了唯一的单值函数y= φ(x)，

将λ带入上式，得：fx(x0,y0)+λΦx(x0，y0)=0

则在φ(x,y)=0的前提条件下，目标函数[5]z=f(x,y)在点(x0, y0)有极值的必要条件为x0,y0,λ满足方程组：

或者记为：F(x,y,λ)=f(x,y)+λφy(x,y)（λ为Lagrange乘数）

n元函数的极值问题为：Min（或Max） f(x)

它的Lagrange函数[6]为：

例1用Lagrange乘数法求解下述问题

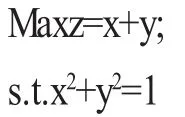
解：令F(x,y,λ)=x+y+λ(x2+y2-1)，x,y,λ满足方程组

（二）可行方向法。若x(k)是非线性规划{minf(x);gi(x)≥0, i=1,2，……，l}的一个可行解，并且不是极小点。为了求它的极小点或近似极小点，要在x(k)点的可行下降方向选取一方向D(k)及确定步长λk，使（R代表可行域）且f(x(k+1))＜f(x(k))，当满足精度要求时，终止迭代，得到的点x(k+1)就是所求的极小点；否则，从(x(k+1)开始继续迭代，到满足精度要求结束，称此方法为可行方向法。

若x(k)点的有效约束集[7]非空，利用下述不等式组来确定x(k)点的可行下降方向D。

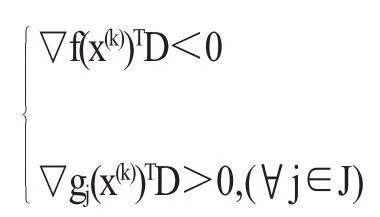
相当于利用下述不等式组求向量D和实数

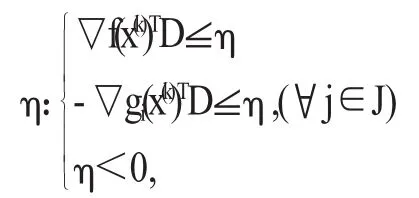
使▽f(x(k))TD和▽-gj(x(k))TD（对于所有的j∈J)的最大值η极小化（同时限制向量D的模），则将上述问题转化为求解线性规划问题。

式中di（i=1,2,……,n）是向量D的各个分量。将式（1）所有的线性规划的最优解记为（D(k),ηk），若ηk=0，则在x(k)点没有可行下降方向，在▽gi(x(k)),(∀j∈J)线性独立的条件下，x(k)点是一个K-T点。若ηk＜0，则得到x(k)点所要的搜索方向D(k)。

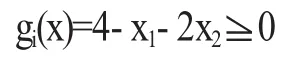
解取初始点 x(0)=(0,0)T，则有 f(x(0))=8．因为▽f(x)=，所以.因为gi(x(0))=4＞0，所以约束条件gi(x)=4-x1-2x2≥0不是初始点x(0)的有效约束．取D(0)=-▽f(x(0))= (4,4)T，从而

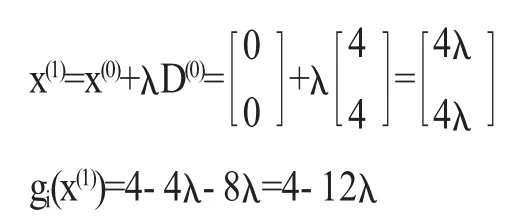
令gi(x(1))=4-12λ=0，可得．而f(x(1))=32λ2-32λ+8

为了便于求解，令y1=d1+1，y2=d2+1,y3=-η于是min(-y3);

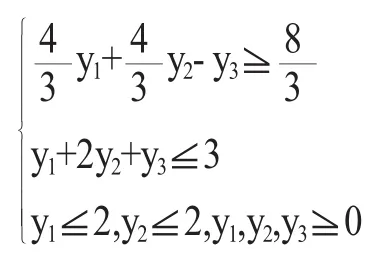
现暂时用此步长计算x(2)，有x(2)=(1.467,1.239)T．由于g1(x(2))=0.055＞0，则x(2)是可行点，λ=0.134是可行的．继续迭代[8]下去，求得最优解x*=(1.6,1.2)T，最优值f(x(*))=0.8。

三、结语

求解非线性规划问题比求解线性规划问题复杂，因为求解非线性规划问题没有一种通用的方法，而求解线性规划问题有一种通用的方法（单纯形法）。本文研究了求解非线性规划约束问题的几种典型方法Lagrange乘数法与可行方向法，当然解决非线性规划求解问题的方法还有很多，如将约束问题化为无约束问题的罚函数法。随着社会的不断发展，新的问题也不断出现，这要求我们在熟悉传统解法的基础上开创新的解法。

[1]吕鹏，潘志.运筹学（数学规划篇）[M].北京:清华大学出版社；北京交通大学出版社，2011:100-150.

[2]希利尔，利伯曼.胡运权等译.运筹学导论（第九版）[M].北京:清华大学出版社，2010:85-86.

[3]马超群，兰秋军.运筹学[M].长沙:湖南大学出版社，2008:300-305.

[4]谢政，李建平.非线性最优化理论与方法[M].北京:高等教育出版社，2010:309-314.

[5]王宜举，修乃华.非线性最优化理论与方法[M].北京:科学出版社，2012:49-68.

[6]袁亚湘.非线性优化计算方法[M].北京:科学出版社，2008:201-210.

[7]大学数学编写委员会编写组.运筹学[M].北京:高等教育出版社，2011:118-209.

[8]HamdyA.Taha.运筹学导论（第八版）[M].薛毅,刘德刚等译.北京:人民邮电出版社，2008:678-685.

[责任编辑郑丽娟]

O222.4

2095-0438（2016）11-0142-03

2016-05-07