动态异方差随机前沿模型的Bayesian推断

程　迪，张世斌（.内蒙古大学数学科学学院，内蒙古呼和浩特000；.上海海事大学数学系，上海浦东0306）

动态异方差随机前沿模型的Bayesian推断

程迪1，张世斌2
（1.内蒙古大学数学科学学院，内蒙古呼和浩特010021；2.上海海事大学数学系，上海浦东201306）

随机前沿模型中如果忽略单边干扰项的异质性（heterogeneity）往往导致错误的效率估计.从个体特征的影响和方差的时变性两方面对单边干扰项进行考虑，提出异方差动态随机前沿模型.利用Gibbs抽样方法对动态异方差随机前沿模型进行Bayesian分析.导出了模型参数的后验条件分布，对中小样本的模拟实验显示在最小后验均方误差准则下得到的参数估计值非常接近真值.对电力公司的实际数据进行分析显示对数无效率项的方差有一定的时变性.

随机前沿模型；Bayesian分析；异方差；Gibbs抽样；Metropolis-Hastings抽样

1　引言

随机前沿模型由Aigner等（1977）［1］及Meeusen和Broeck（1977）［2］提出，被广泛用于衡量经济效率.随机前沿模型将误差项分为对称误差项和单边干扰项两部分，分别反映了测量误差和模型中的技术无效率对产出或成本造成的负面影响，即单边干扰项又为无效率项.通常假定无效率项在所有决策单元中是独立同分布的，无效率项的分布一般假设为半正态分布［1］，指数分布［2］，截断正态分布［3］，Gamma分布［4］或倒Gamma分布［5］等.然而，影响一个公司效率的因素除了成本函数模型中的输入输出变量，还包括一些公司特征，如公司的所有权，公司政策的改变，行业的竞争等.这些因素将对公司的效率产生一定的影响.如果公司的这些特征产生异质性（heterogeneity）或者对单边干扰项产生影响，这些特征就可以在前沿模型中表现出来.文［6］将协变量直接以函数形式表现并研究了单边干扰项中未被观察到的异质性.文［7］针对多输出随机前沿模型，提出用copula函数来刻画无效率项分布.文［8］提出了动态随机前沿模型，无效率项随着时间的变化而变化，并用Bayesian分析和MCMC方法对参数进行估计.文［9］将随机前沿模型进行转换，消去个体的固有影响，并对其参数估计的一致性进行分析.文［10］对无效率项服从广义Gamm a分布和广义混合Gamma分布的随机前沿模型进行Bayesian分析，考虑了无效率项中可观察到的异方差.文［11］提出用参数来刻画未被观测到的异质性，指出了异质性可能影响的变量并通过实例对变量进行分析论证.

现有随机前沿模型较少涉及无效率项中未观测到的异质性，本文提出用GARCH（p，q）来刻画对数无效率项.其中，均值方程刻画可以观测到的异质性，条件方差方程刻画未观测到的异质性.当p=q=0时对数无效率项方差为常数，无效率项不存在异方差.否则，对数无效率项方差是过去误差项和滞后条件方差的函数，随时间变化方差的值不同.本文利用Gibbs抽样对动态异方差随机前沿模型进行Bayesian分析.通过对模型参数选取合理的先验分布，导出模型参数的后验条件分布，并给出了Gibbs抽样的具体策略.由于参数λ和α的后验条件分布不是标准密度函数，且极难找到标准分布的密度函数作为控制函数进行舍选，常用的随机游走抽样和G riddy-Gibbs抽样方法在该分层随机前沿模型中的舍选效率非常低.本文参照Nakatsum a（参见［12］）提出的近似GARCH模型方法，将条件方差方程构造成新的ARMA方程，得到参数的建议分布，最后通过Metropolis-Hastings抽样实现对参数λ和α的抽样.此方法大大提高了动态异方差随机前沿模型的计算效率.

2　模型介绍

与截面数据相比，面板数据更能提供对公司技术效率的可靠估计.考虑随机前沿模型

其中yit表示第i个个体t时间的产出，xit为k×1维向量，表示第i个个体t时间的投¡入，β¢是k×1的参数向量.vit是统计误差，设vit关于i和t相互独立并且有相同的分布vit～N 0，σ2.uit是无效率项，为非负的随机变量.假设vit和uit相互独立，且无效率项uit满足

对所有的i，t都有ξit～N（0，1）且相互独立，zit为m×1维的协变量，γ为m×1维的参数向量.这里γ用来描述无效率项对数中可以观测到的异质性，未能观测到的异质性服从N（0，hit）.方差hit为GARCH（p，q）模型，当λ1=···=λp=α1=···=αq=0时，hit恒为常数λ0，即无效率项uit不存在异方差，否则方差hit随时间变化，依赖于其以前时刻的方差和式（1）中的扰动项平方.现有文献中较多的涉及无效率项中已观测到的异质性，而对未观察到的异质性研究较少，文［8］和［11］中假设未观测到的异质性服从一定分布.本文在已有文献的基础上，用协变量表示无效率中可以观测到的异质性.对未观察到的异质性，通过假设对数无效率项方差为以前时刻方差和扰动平方项的线性组合，讨论无效率项中未观测到的异质性及其变化规律.

y和u的联合分布为

3　Bayesian分析及抽样方法

本节对动态异方差随机前沿模型进行Bayesian分析并采用Gibbs抽样方法对模拟参数的后验均值进行推断.首先确定参数的先验分布，先验分布的选取应满足相容性原则，即随着样本量的增大，先验信息的影响减弱.假设参数β，γ，α，λ和尺度参数σ2相互独立，则参数β，γ，α，λ的联合先验具有形式

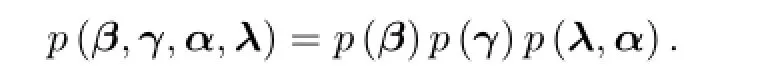
由于参数的先验信息很难得到，而不恰当的先验会对模拟结果产生影响.因此，参数β，γ，α，λ的先验皆选为无信息先验.另外，为确保方差hit为正和模型的平稳性，系数λ和α必须满足λi≥0，αi≥0和

那么，参数β，γ，α，λ的联合先验可以写为

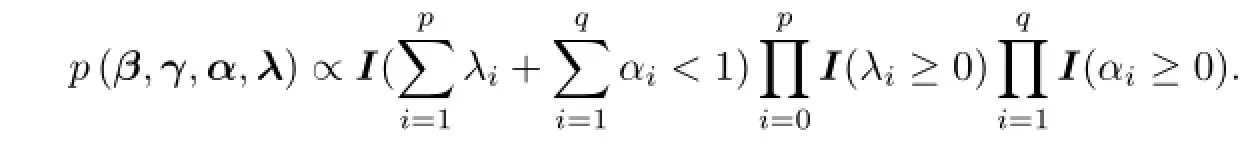
其中，I（·）为示性函数.

尺度参数σ2的先验分布可取倒Gamma分布（参见［13］），即

其中，p0＞0和q0＞0为先验分布的参数.

由Bayesian理论，将参数的先验分布和样本信息综合可得到参数后验分布.θ和u的联合后验分布为

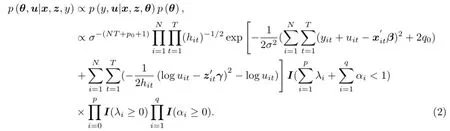
为对模型进行预测或参数推断，Bayesian模型往往需要对高维概率密度分布进行积分. MCMC是一种解决高维积分问题的迭代Monte Carlo方法，它解决了复杂表达式难以进行高维积分的问题，应用非常广泛.MCMC通过利用M arkov链进行积分得到一系列的M arkov链模拟值，该链的平稳分布收敛到已知参数的后验分布，即可看作后验分布的独立样本.Gibbs抽样是一种最常见且最简单的MCMC方法，这里使用Gibbs抽样方法对参数后验均值进行推断.为了使MCMC方法产生的Markov链的平稳分布是（2），下面讨论Gibbs抽样方法的具体策略.设Gibbs抽样得到的Markov链

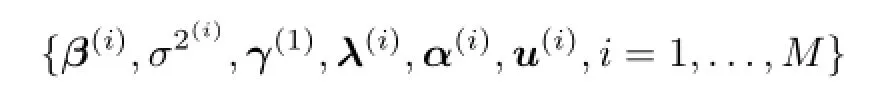
收敛到已知的参数后验分布.因此，参数后验期望可以通过Gibbs抽样得到的平均值来近似，即

下面对参数抽样的具体策略进行分析.由（2）式可得到每个参数后验分布的核.

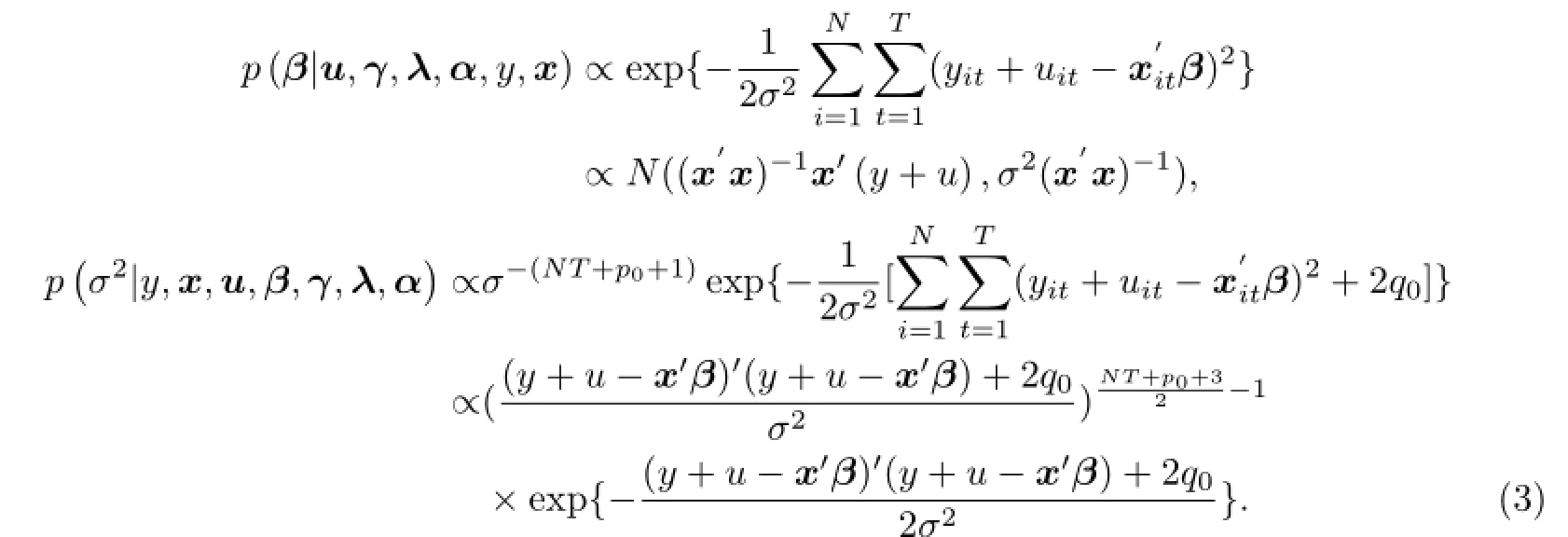
其中，x为（N·T）×k矩阵，y为（N·T）×1矩阵.由（3）式可知，

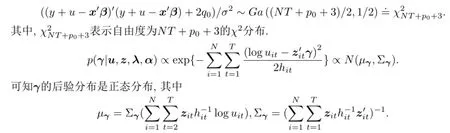
参数β，γ和σ2的后验条件分布都为标准分布，可直接进行抽样.

隐含变量uit的后验分布随着时间变化，第i个公司t时刻无效率项uit的后验分布为

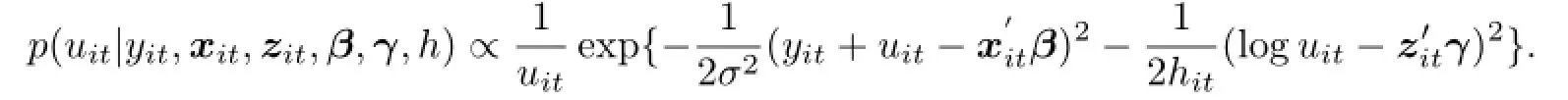
其后验分布不是标准分布，不能进行直接抽样，可以通过切片抽样或舍选抽样得到.文中使用的是切片抽样方法，产生uit的具体步骤见算法1.

文中令

其中

从后验分布可知，在给定参数u，γ的前提下，参数λ和α中给定任意一个参数的值，另一个参数的条件后验核密度函数都不是标准分布密度函数.在这里取样方法参照Nakatsum a（参见［12］）所提议的近似GARCH模型，用Metropolis-Hastings抽样方法对其进行抽样.令

式

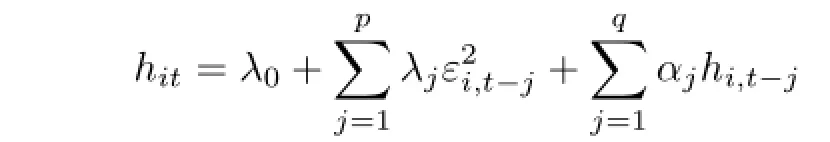
其中l=m ax｛p，q｝，且有

以λ的取样为例，Metropolis-Hastings抽样方法的具体步骤为：

算法2（产生λ）

步1从建议分布π（λ）中抽取λ′.

步2从U（0，1）中抽取e.

算法2中λ的建议分布需要主观设定，近似GARCH的似然函数可以写为：

其中，

那么，λ建议分布为

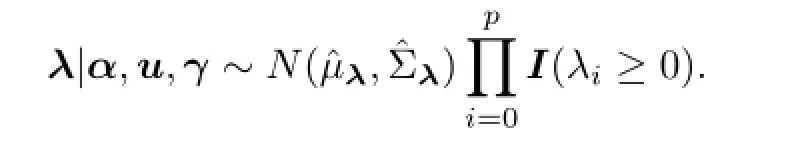
这里，

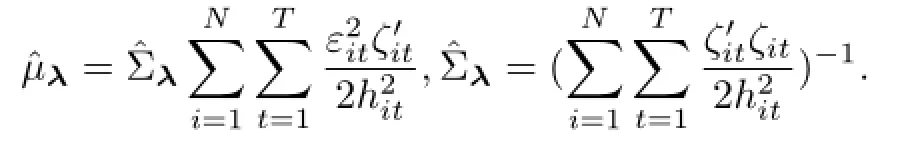
为生成α的建议分布，将wit（α）在α∗处用Tay lor展式展至一次项，则近似GARCH模型的似然函数为

上式中α∗是α的加权非线性最小二乘估计值，即

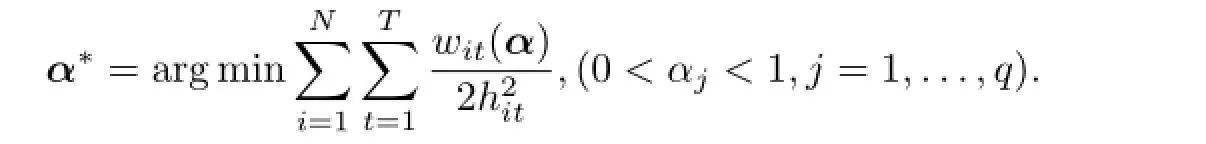
其中ζitj是wit在点处的一阶导数值的相反数.又

则有

那么，参数α的建议分布为

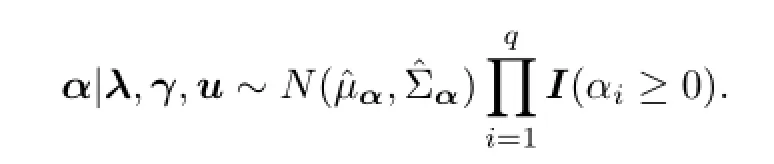
令

则

4　模拟实验

为验证Gibbs抽样方法的效果，这里进行了模拟实验.为方便计算，令p=q=1并对两个公司的情况进行模拟，考虑如下模型：

取k=3，m=3，xit，zit的第一列均取1，为表现出相关性，xit，zit的剩余k-1列的元素从二元标准正态分布中随机产生，两者的相关系数为0.5，如文［14］.取参数β真值为［1，1，1］′，γ真值为［-0.3，1，1］′.取σ2=0.05，λ0=0.05，λ1=0.2，α1=0.7.对于先验分布的参数分别取p0=4，q0=0.01.分别取样本量100，500和1000三种情况来进行模拟比较，模拟轨道长度60000并抛去轨道的前10000个点.各参数后验估计值和后验标准差见表1.

表1　参数后验均值结果

由表1，对比各个参数的真值和估计值，参数β的估计值在样本量很小时就非常接近真实值，参数z的估计值样本量很小时就很接近真值.参数λ0，λ1，α1和σ2在样本量小时接近真值，参数的估计随着样本量的增大，模拟效果变好.参数的后验标准差随着样本量的增大明显减小，特别是参数λ0，λ1和α1，在样本量较小时标准差较大，随着样本量的增大明显减小.可见，用Gibbs抽样对动态异方差随机前沿模型进行Bayesian分析有比较好的效果.在模拟实验过程中发现，当样本量较小特别是公司多时间短的情况下，λ0的模拟值会出现均非常接近于零的情况，使hit的后验均值几乎为零，即参数估计结果中无效率项方差估计值非常小.这是因为，λ0的抽样采用的是M etropolis-Hasting算法.在抽样过程中，一旦在一步中出现λ0的模拟值很接近于零时，λ0的建议分布的方差将很小，使得Metropolis-Hasting抽样更新效率极低.而当样本抽样时间区间很短时，极易出现在某一步迭代中λ0的模拟值非常接近于零的情况.将λ0的先验由无信息先验变为均匀分布U［δ，1］，其中δ为一很小的正数，可避免λ0的模拟值几乎为零的情况.

5　实证研究

将本文模型应用于哥伦比亚电力改革.样本数据来自文［15］中，取自1998-2012年哥伦比亚的电力分销公司，本文对原始数据进行筛选，取出其中时间序列较长的12个公司共174个观察值.考虑如下随机前沿模型，

其中，yit，x1it，x2it分别表示第i个公司t时刻的输入总费用，输出总能量和消费者数量.无效率项异方差变量zit为第i个公司t时刻的用户密度.数据和模型的进一步解释可参见文［16］.先验参数取值与模拟实验部分的值一致，p和q的值均取1.G ibbs抽样模拟轨道长60000并抛去模拟轨道的前10000个点.主要参数的后验均值和标准差见表2，其中括号中数字为参数后验标准差.

表2　参数后验均值结果

由表2可知，从γ的估计值可以看出，公司的用户密度会对效率产生一定的影响.参数λ0的估计值为0.011，而λ1和α1的估计值分别为0.192和0.160，说明对数无效率项的方差依赖于过去误差项和滞后条件误差.可见，随机前沿模型中不能忽略公司特征引起的异方差和方差的时变性.实例主要研究了条件方差hit为GARCH（1，1）的情况，未对高阶的情况进行深入研究.另外，可以将本文与文［8］和［11］进行结合，对无效率项进行更全面的诠释.

［1］Aigner D，Knox-Lovell C A，Schm dt P.Formu lation and estimation of stochastic frontier production function m odels［J］.J Econom etrics，1977，6:21-37.

［2］M eeusen W，van der B roeck J.E fficiency estim ation from Cobb-Douglas p roduction functions w ith Com posed Error［J］.Internat Econom Rev，1977，18:435-444.

［3］Stevenson R E.Likelihood functions for generalized stochastic frontier model［J］.J Econom etrics，1980，13:57-66.

［4］G reene W H.A gamm a-d istributed stochastic frontier m odel［J］.J Econom etrics，1994，61: 273-303.

［5］刘晓君，张世斌.正态倒Gamm a随机前沿模型的Bayesian推断［J］.高校应用数学报，2013，28（4）: 488-496.

［6］Greene W.Reconsidering heterogeneity in panel data estimators of the stochastic frontier model［J］.J Econometrics，2005，126:269-303.

［7］Carta A，SteelM F J.M odellingmu lti-output stochastic frontiers using copu las［J］.Com put Statist Data Anal，2012，56:3757-3773.

［8］Tsionas E.In ference in dynam ic stochastic frontier models［J］.J App l Econom，2006，21: 669-676.

［9］Chen Y i-Y i，Schm id t P，W ang Hung-Jen.Consistent estim ation of the fixed effects stochastic frontiermodel［J］.J Econometrics，2014，181:65-76.

［10］Griffin J，Steel M.Flexiblem ixturemodelling of stochastic frontiers［J］.J Prod Anal，2008，29:33-50.

［11］Galán J，Veiga H，W iper M.Bayesian estimation of inefficiency heterogeneity in stochastic frontiermodels［J］.J Prod Anal，2014，42:85-101.

［12］Nakatsuma T.Bayesian Analysis of ARMA-GARCH Models：A Markov chain Sam pling Approach［J］.J Econometrics，2000，95:57-69.

［13］Fernandez C，Osiewalski J，Steel M F J.On the use of panel data in stochastic frontier models［J］.J Econometrics，1997，79:169-193.

［14］Wang Hung-Jen，Schm id t P.One step and two step estimation of the effects of exogenous variables on technical efficiency levels［J］.Prod Anal，2002，18:129-144.

［15］Galán J E，Pollitt M.Inefficiency persistence and heterogeneity in Colombian electricity utilities［J］.Energ Econ，2014，46:31-44.

［16］Grow itsch T，Jamasb T，Pollitt M.Quality of service，efficiency and scale in network industries:an analysis of European electricity d istribu tion［J］.App l Econ，2005，41:2555-2570.

M R Sub ject C lassification:62F15；65C60

Bayesian in ference for dynam ic heterogeneity stochastic fron tier m odel

CHENG D i1，ZHANG Shi-bin2
（1.School of M ath.Sci.，Inner M ongolian Univ.，Hohhot 010021，China；2.Dept.of M ath.，Shanghai M aritim e Univ.，Shanghai201306，China）

If heterogeneity of the“inefficiency”term is disregarded，it w ill resu lt in the incorrect estim ate of this term in the stochastic frontier m odel.By com bining the in fluence from characteristic differencesof individualsw ith the time-varying property of variance，a dynam ic heterogeneity stochastic frontier m odel is p roposed.By the G ibbs sam p ling，the m ethodology for Bayesian analysis of the dynam ic heterogeneity stochastic frontier model is given.For each model parameter，the posterior distribu tion is derived.A sim ulation study show s that under the criterion ofm inim izing the posterior mean square error，the Bayesian estimate is close to its true value for small and medium sized sam p les. From the Bayesian analysis based on the real electric pow er com pany generation data，it is evidenced that there exists the time-varying p roperty for the variance of the logarithm“inefficiency”term.

stochastic frontiermodel；Bayesian inference；heterogeneity；Gibbs sam p ling；Metropolis-Hastings sam p ling

O212.8

A

1000-4424（2016）02-0127-09

2015-11-13

2016-04-19

上海市自然科学基金（13ZR1419100）；上海市教委科研创新项目（14YZ115）