习题课教学：值得关注的多元表征理论——以2016年山西省中考第23题为例

☉江苏省无锡市河埒中学　顾　雪

习题课教学：值得关注的多元表征理论——以2016年山西省中考第23题为例

☉江苏省无锡市河埒中学顾雪

抛物线为载体的综合题常常综合平面几何的性质进行考查，中考复习过程中的习题课教学时如何重视这类试题的研发与变式应用，是值得很多毕业年级教师认真思考的课题.本文以2016年山西省中考第23题为例，先给出解题思路和解后反思，并围绕考题开展教学微设计，供研讨.

一、考题的思路突破与解后反思

考题（2016年山西省，第23题）如图1，在平面直角坐标系中，已知抛物线y=ax2+bx-8与x轴交于A、B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A、D的坐标分别为（-2，0）、（6，-8）.

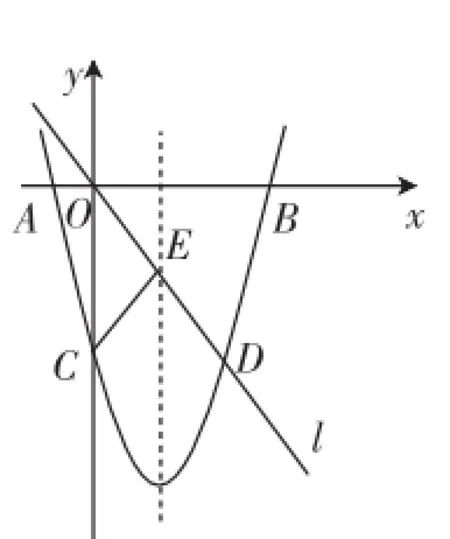
图1　

（1）求抛物线的函数表达式，并分别求出点B和点E的坐标.

（2）试探究抛物线上是否存在点F，使△FOE≌△FCE.若存在，请直接写出点F的坐标；若不存在，请说明理由.

（3）若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点Q，试探究：当m为何值时，△OPQ是等腰三角形？

思路突破：

（1）把A（-2，0）、D（6，-8）两点的坐标代入抛物线y= ax2+bx-8的解析式，解关于a、b的二元一次方程组，得到，即抛物线的解析式为于是抛物线的对称轴为x=3.再结合条件：点A（-2，0）与点B关于对称轴对称，可以求出点B的坐标为（8，0）；因为直线l经过坐标原点O与点D（6，-8），只要把点D的坐标代入直线l的解析式y=kx可得因为点E是直线与抛物线的对称轴x=3的交点，把x=3代入直线l的解析式即可求出点E的坐标（3，-4）.

（2）先假设存在，然后展开探究.由△FOE≌△FCE可知FO=FC，EO=EC，即点F的纵坐标c. 因为点C是抛物线与y轴的交点，当x=0时，代入抛物线解析式得y=-8，点C的坐标为（0，-8），即yF=-4，构造图2示意.

由图2示意知，直线y=-4与抛物线的两个交点F1、F2即为所求.只要将yF=-4代入抛物线的解析式8，得到一个一元二次方程解得x1=3+所以抛物线上存在点或使△FOE≌△FCE.

（3）首先分析△OPQ是等腰三角形的一些可能情形，考虑到点P是y轴负半轴上的一个动点，所以只有两种可能的情况：OP=OQ或PQ=OQ.

①如图3，当OP=OQ时，△OPQ是等腰三角形.

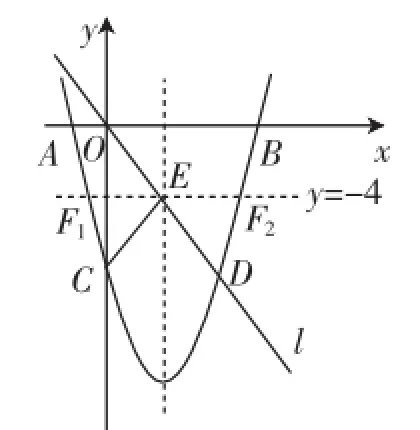
图2　

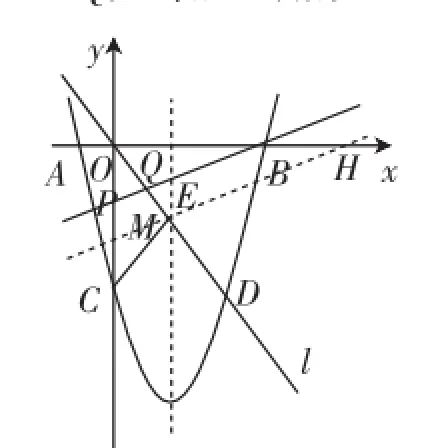
图3　

此时直线PB与直线l的交点Q在线段OE上，结合点E的坐标为（3，-4），可得OE=5.考虑过点E作ME∥PB交y轴于点M，交x轴于点H，利用相似三角形（或平行线分线段成比例）可得得到OM=OE=5，从而得到点M的坐标为（0，-5）.设直线ME的解析式为y=k1x-5，把点E的坐标代入解析式y=k1x-5，解得所以直线ME的解析式为当y=0时，即可得它与x轴的交点H的坐标为（15，0）.由MH∥PB可得即求出

②如图4，当PQ=OQ时，△OPQ是等腰三角形.

图4　

此时直线PB与直线l的交点Q在线段OE的延长线上.由抛物线y与y轴的交点C的坐标为（0， -8），利用勾股定理求得CE的长为5.又OE=5，所以OE= CE，即∠EOC=∠ECO.由PQ=OQ可知∠QOP=∠QPO，即∠ECO=∠QPO，可得CE∥PQ.利用比例式即求出

二、解题教学的“微设计”

教学环节（一）：开课阶段，熟悉平台

图5　

例1如图5，在平面直角坐标系中，已知抛物线y=ax2+bx-8与x轴交于A（-2，0）、B两点，交y轴于点C，且该抛物线的对称轴为直线x=3.

（1）求点B的坐标.

（2）求△ABC的面积.

（3）直线l经过坐标原点O，与抛物线的一个交点为N（6，n）.

①求证：CN∥x轴；

②设直线l与对称轴x=3交于D点，请指出△OCD的形状，并说明理由.

设计意图：改编原考题，以一些简单的问题，促进学生思考该抛物线的解析式如何求，怎样确定抛物线与坐标轴的交点坐标，并初步理解直线l与抛物线的交点问题.

教学环节（二）：动点探究，渐次生长

（1）直接写出该抛物线的对称轴；

（2）求k的值；

（3）若抛物线的对称轴与直线y=kx交于E点，连接CE，求tan∠OCE的值；

（4）若点F是抛物线上一个动点，当△FOE≌△FCE时，求点F的坐标.

设计意图：主要是针对原考题的第（2）问进行训练，通过增设铺垫式问题，使得问题的难点分散开来，吸引更多学生的思维参与.

教学环节（三）：动点探究，渐次生长

（1）当OP=PE时，求直线PB的解析式；

（2）当△APE为等腰三角形时，求点Q的坐标；

（3）当△OPQ为等腰三角形时，求点P的坐标；

（4）若抛物线在第四象限有一点M，当△MOD的面积最大时，求点M的坐标.

设计意图：前三问主要围绕原考题的最后一问进行变式探究，最后一问则是将问题拓展到“抛物线弓形三角形面积最值问题”，而且需要考虑两种情况，即点M在线段CD、线段BD上时，较难的是在线段CD上时，可以将直线OD向下平移，与抛物线相切时取得最大值.

教学环节（四）：听课检测，学情反馈

听课检测题：如图1，在平面直角坐标系中，已知抛物线y=a（x+2）（x-6）与x轴交于A、B两点，交y轴于点C.直线y=kx分别交该抛物线及其对称轴于点D、E（3，-4）.

（1）求k的值；

（2）求证：△COE是等腰三角形；

（3）若点P是y轴负半轴上一个动点，当△OPD为等腰三角形时，求点P的坐标；

（4）设M、N分别在y轴、直线y=kx上，当M、N、B三点在同一直线上，且△OMN～△OCE时，求点N的坐标.

三、教后感

以抛物线为载体的综合题常常综合了很多平面几何的性质，比如全等、相似、等腰三角形、勾股定理、锐角三角函数等性质，如果就题讲题，教学效果会大打折扣.如果能在课前深刻理解待讲考题的思路、结构，并精心设计系列问题，特别是铺垫式问题，则可取得较好的教学效果.

1.精选考题，注重基础，渐次生长，拓展延伸

题海茫茫，如何在众多考题中挑选出适合本地区使用的是习题讲评时首先要思考的.具体来说，首先是优选本地区的经典考题，在此基础上变式改编，在课堂前半段要重视基础的训练，让更多学生的思维参与，课堂后半程再渐次生长，引出考题训练的难点，并通过必要的设问，启发点拨，攻克难点.

2.预设追问，多元表征，变式检测，注重反馈

在教学设计的同时，针对各个不同教学环节，要注意预设系列追问，使得教学过程走向开放，也给学生展示交流的机会.系列追问在设计时要注重基于多元表征的理论，即不同的设问整体上要围绕一个主题设问，加强设问题组的针对性，而不能问得太过发散，使得训练的指向过于宽广，避免前后设问之间缺少必要的关联.教学最后，针对教学过程中的变式问题，给出一道变式检测题，各个小问分别对应着前面所讲评的重点问题，以便检测听课效果.

1.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.

2.钟启泉.读懂课堂［M］.上海：华东师范大学出版社，2015.

3.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

4.郑毓信.善于提问［J］.人民教育，2008（19）.Z