从一道中考题剖析几何中有关圆的问题

江苏省海门市四甲初级中学　张　丹

从一道中考题剖析几何中有关圆的问题

江苏省海门市四甲初级中学张丹

数学的几何试题是一种将计算与平面证明融为一起的推断问题，真正体现了逻辑思维的运用。很多初中学生的逻辑思维能力不强，做题的过程推理不严密，时有“卡壳”现象，究其原因在于储存的几何知识欠缺。当几何试题中有圆图形出现时，更是底气不足，一个重要的原因就是对有圆的图形所涉及到的内涵和外延都是一知半解。不能够挖掘内涵，就找不到要素的对应关系；不能理顺外延，就排除不了试题设置的障碍。怎样才能做到充分认识几何试题中圆涉及到的内涵和外延呢？本文从2016年的江苏南通的一道中考试题说起，通过剖析试题让我们再次领略中考试题的风采，找寻其试题的奥秘所在。

中考；剖析；圆；几何

进入初三，学生面临的升学压力越来越大，自然而然觉得掌握的数学知识越来越不够用。几何问题从线形的变换到数值计算的容易，使学生“压力山大”。包涵着逻辑推理的几何问题在学生的认知层面开始深化，体现数形转换的数学思想在学生的思维里悄无声息的形成。这是一个关键时期，是为高中乃至于大学的学习打下基础的阶段，让学生真正能够形成学科素养。

一、剖析典例挖掘试题的真正内涵

【例题】（2016年南通市初中毕业升学考试数学试题）已知：如图1，AM为⊙O的切线，A为切点，过⊙O上一点B作BD⊥AM于点D，BD交⊙O于C，OC平分∠AOB

（1）求∠AOB的度数

（2）若⊙O的半径为2cm，求线段CD的长

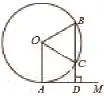
图1

【试题分析】从图形可知，AM是⊙O的切线，BD是⊙O的割线，OA与BD平行，可以发现一些特殊的图形，如四边形AOBD是直角梯形。另一方面OC是一条角平分线，它有平分角的作用，能否形成特殊角？只有认真去挖掘图形中的这些内涵，就可以找到解决问题的方法。

（1）根据题干已知OC平分∠AOB，就可以得出平分得到的两个角相等，即是∠AOC=∠COB；必须将这两个相等的角应用到推理中去。

根据题干已知AM切⊙O于点A，可以挖掘出来OA⊥AM，再由已知BD⊥AM，就能得到OA∥BD，由夹在平行线中的内错角相等推断出∠AOC=∠OCB。

利用同圆的半径相等来分析△OBC，OC=OB，△OBC是等腰三角形，而∠OCB=∠B，等腰三角形的顶角和底角相同，说明△OBC是等边三角形，因此就可以得到∠B=∠OCB=∠COB=60°，故可以推断∠AOB=120°

（2）方法是多样的，可以真正体验圆所涉及到的内涵和外延。方法1：可以在等边三角形△OBC中，过点O作辅助线OE⊥BC于E，即是等边△OBC边BC上的高，如下图2：

图2

可知四边形AOED为矩形，矩形的对边相等，⊙O的半径为2cm，即OD=AO=2cm；

在由BC=2cm，CE=BE=1cm得出CD=BE=CE=1cm

方法2：连接AC，如图3。因为∠OCA=∠AOC=60°，直角三角形ACD是特殊角三角形。

图3

△AOC≌△COB，是对边三角形，AC=2cm，推断出OD=AC=1cm。

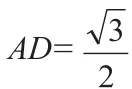
二、分析典例体验命题的发展方向

从以上典例分析可以发现，中考试题注重考查的是几何的基础知识、解题的基本技能，因此在指导学生学习时必须从基本数学思想方法的认知和应用等方面出发，紧扣分析和解决问题的方法培养。

（1）因为试题关注了对几何的基础知识和基本技能的考查，所以，在这里试题的分析过程中需要利用圆丰富的元素将复杂几何图形中分解成为简单、基本的图形，如等腰三角形、直角三角形等，从而提升学生利用基本图形挖掘基本元素之间的关系的能力。

（2）无论是几何证明题还是几何计算题，推理论证是必要的过程，在平时学习中可以借助于圆中的直径、半径、圆周角等元素的特征，整合学生已掌握的基本数学活动经验，并将这些已有的经验进行灵活的运用。

（3）在平时的学习中要不断地挖掘圆的元素及其内涵，譬如直径所对的圆周角为直角，可以构成直角三角形，也可以分散到两条直线垂直知识方面；另外还可以从圆的外延出发，用一些熟知的定理如切割线定理、相交线定理来证明或者计算有关圆的几何问题，不断丰富学生的解题方法和技巧。

总之，通过2016年的江苏南通的一道有关圆的经典中考试题的剖析，让我们不但领略到了中考试题的风采，而且通过试题探究明确了其真正的内涵以及所折射出来的外延。

［1］何国伟，杨德焱.一道中考几何计算题解法的探究与启示［J］.《中国数学教育》，2011（5）：16-18.

［2］吴永刚.在偶然与必然之间徜徉探究——对一道中考几何试题的再研究［J］.《中学数学》，2010（10）：60-61.

［3］张宏政.几何题的分析首先从逻辑关系入手——从一道中考错题谈起［J］.《中学数学教学参考》，2013（1）：62-64.