SVM参数优化方法分析与决策

郭克友,郭晓丽,王艺伟

(北京工商大学 材料与机械工程学院，北京 100048)



SVM参数优化方法分析与决策

郭克友,郭晓丽,王艺伟

(北京工商大学 材料与机械工程学院，北京 100048)

针对支持向量机应用过程中的参数选择问题，从UCI数据库选择样本集，分别采用传统的网格法、智能优化算法中的粒子群法及遗传算法实现核函数参数寻优过程，将所得最佳参数应用到样本测试中;在深入分析优化过程中各参数关系、参数对支持向量机性能的影响以及传统与智能优化算法的优劣后，得出了核函数优化策略;即先使用智能优化算法初步确定最优解范围，再结合网格法进行高精度寻优;实验数据验证了参数优化策略的有效性，为扩大支持向量机泛化率、提高应用性做了铺垫。

支持向量机；核函数；传统优化算法; 智能优化算法

0 引言

支持向量机(support vector machine, SVM)，可利用核函数在原空间直接计算，既能避免“维数灾难”，又能高效地解决非线性分类问题，成为浅层机器学习算法中的优秀代表。人工神经网络和基于规则的分类器是以贪心学习为策略对假设空间搜索最优解，但容易陷入局部解，而且会出现“过拟合”[1]。SVM可以表示为凸优化问题，一般依靠小样本进行训练学习，将待分类问题转化到高维线性可分空间，找到最大分类间隔，得到目标函数的全局最优解。Vapnik等人[2-3]的研究成果表明，在解决实际问题时，核函数的参数及惩罚因子对SVM性能影响很大，因此研究参数选取问题具有很大的意义。

1 数据准备

样本来自加州大学欧文分校(University of CaliforniaIrvine)的UCI数据库[4]。该数据库中为样本提供了特征向量，可避免使用者设计特征提取算法或因主观因素而造成的特征选取不当问题。实验中将类别标签命名为1、2等数字，样本按8:2随机划分为训练和测试样本。为充分利用给定数据集，降低VC维，训练过程采用交叉验证法的思想。选取的数据集信息如表1所示，基本分布如图1。经过多次试验测试，得到如下实验数据集选取原则：

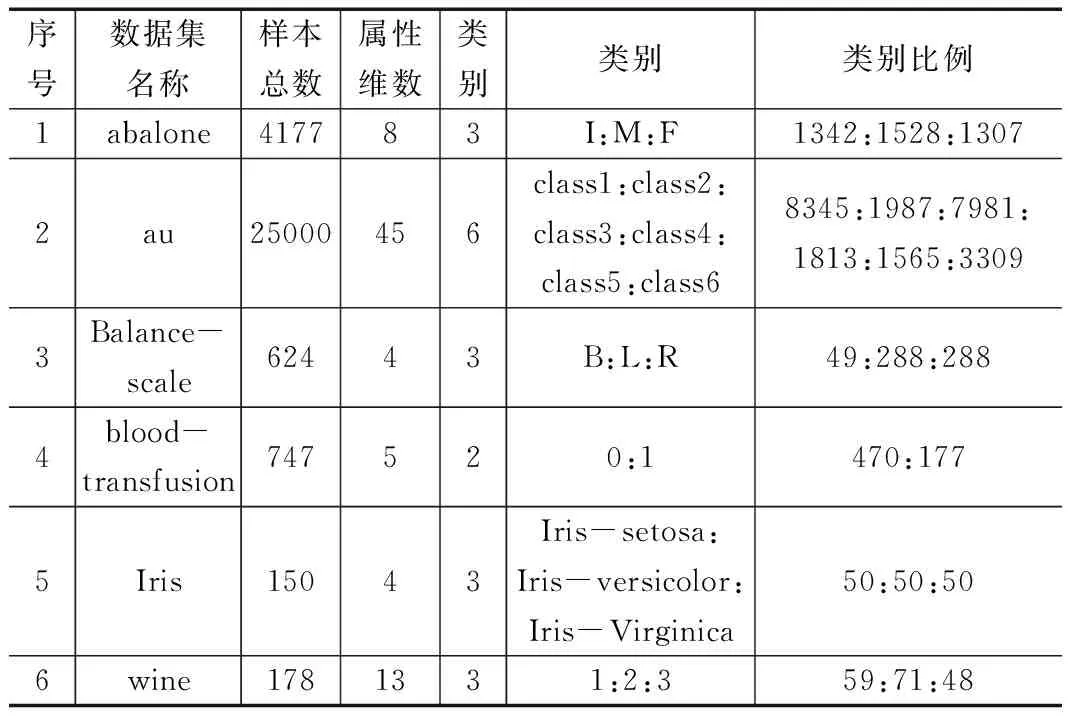
表1 UCI标准数据库部分数据

1)数据集的实例个体数目分布多样化；

2)实例的特征向量维数多样化，因为维数对机器学习训练时间和模型影响较大；

3)应包含二分类和多分类情况；

4)样本类别应均衡分布，针对不均衡或欠采样的数据，SVM需做其他处理，或难以确定分类器性能[5-6]。

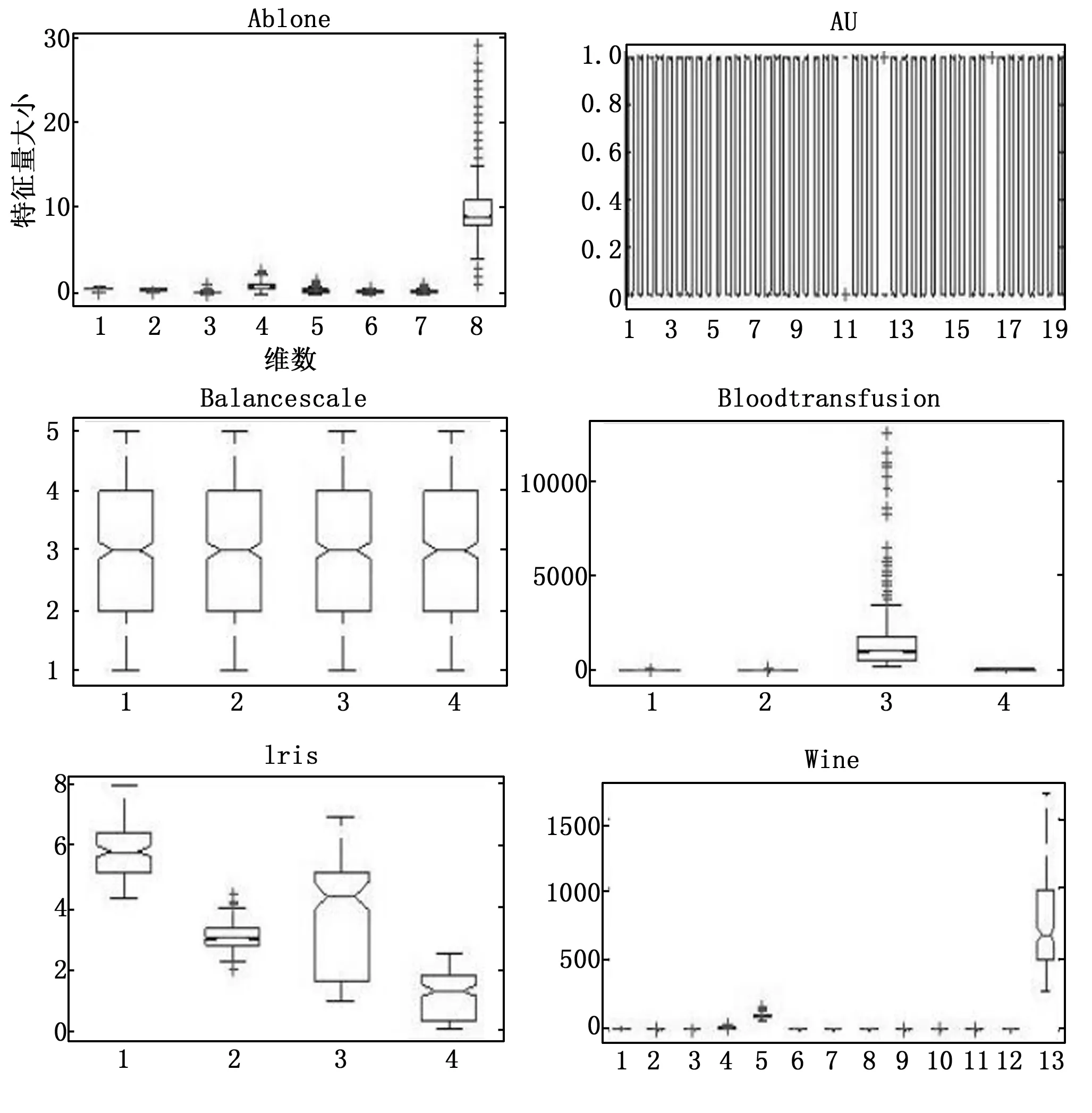
图1 数据集样本分布盒图

图1显示了Abalone、Au和Wine数据集的特征向量维数较多，Abalone、blood-transfusion 和wine数据集个别向量在维度上的值跨度较大。Balance-scale数据集分布较为均衡。

2 数据预处理多参数全局车道线检测模型

2.1 数据归一化

特征向量属性不同，在数值分布上的差别会导致奇异样本数据，引起网络不收敛，训练时间增长等问题，所以需要对特征进行数量级统一，即归一化。国内外学者的研究表明，在代价函数中，奇异样本数据中的大值特征分量对结果的影响大于小值特征分量，特征归一化会使分类器的识别率提高，加快训练速度[7]，归一化公式如(1)所示：

(1)

其中：xi为样本集，yi为归一化后的值。

考虑每个维度的量纲不同，且数量级差别悬殊，为尽量减少样本原始信息的丢失，应对每个维度单独归一化。经对图1数据分布盒形图分析，将数据集按照公式式(1)进行归一化到[-1,1]区间，归一化前后数据集样本分布如图2所示。

图2 归一化后数据集样本分布

2.2 PCA数据降维

统计学上，SVM的基础是VC维理论和结构风险最小原理。在保证分类精度的同时，尽量降低机器学习的VC维，才能使模型在给定数据上的期望风险得到有效控制。降低VC维重要的手段就是对样本的特征向量进行降维处理。主成分分析法(principal component analysis, PCA)在最小均方意义下寻找最能代表原始数据的投影方向，能保存数据内在结构和原始信息，已成功运用在人脸识别领域。本文所用实验数据维数范围是4～45，根据一般降维原则，提取90%的主成分。6个数据集的成分占比如图3所示。

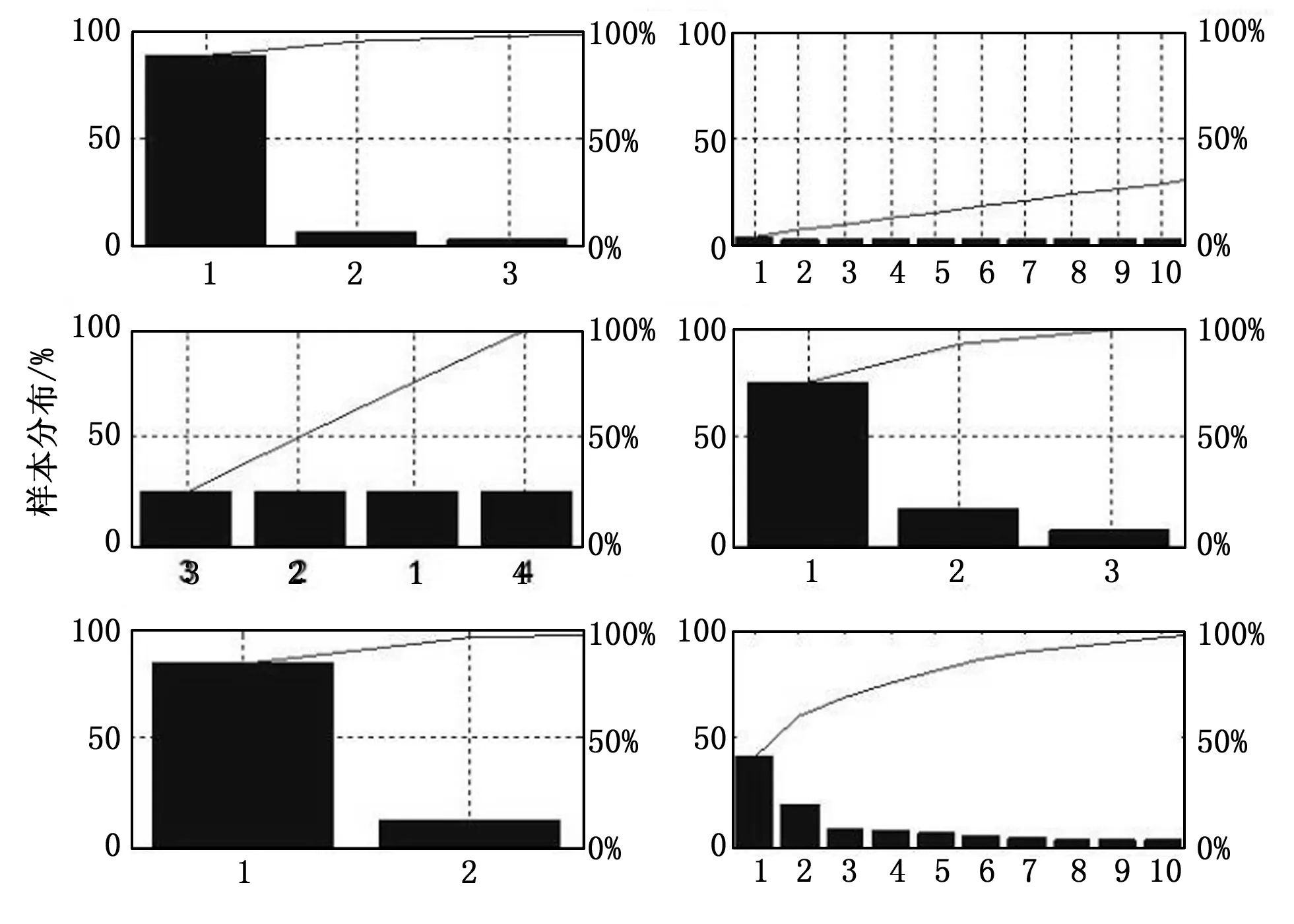
图3 数据集主样本分布

3 SVM核函数参数选取

支持向量机通过引进内积核函数巧妙的解决了高维空间中的内积运算，而不同的核函数选择也构成了不同的支持向量机。常用的核函数有：线性核、多项式核、高斯核、二层神经收集核，一般高斯核最为有效[8]。设定2分类问题，在SVM理论中，若将SVM分类超平面记为l(i)，表示其相似度的高斯核函数记为f(i)，如式(2)。则高斯支持向量机的目标函数(cost function)F可记为式(3)：

(2)

(3)

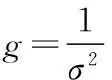
3.1 网格算法参数寻优

网格算法属传统优化算法的一种，其实质是穷举法，随着排列组合情况增多，运算量急剧增加。但在实现过程中，能较好的找到最优参数的分布范围，即参数组合的“好区”[9]，摆脱局部最优解，得到一定精度下的全局最优解。本文中C和g取值为[2^(-5),2^(-4),…,2^8,2^9 ]，共255个(C,σ2)组合。数据集经预处理后进行参数训练，图4显示了数据集1 以网格法进行参数寻优的过程，表2汇总了6个数据集的训练情况。

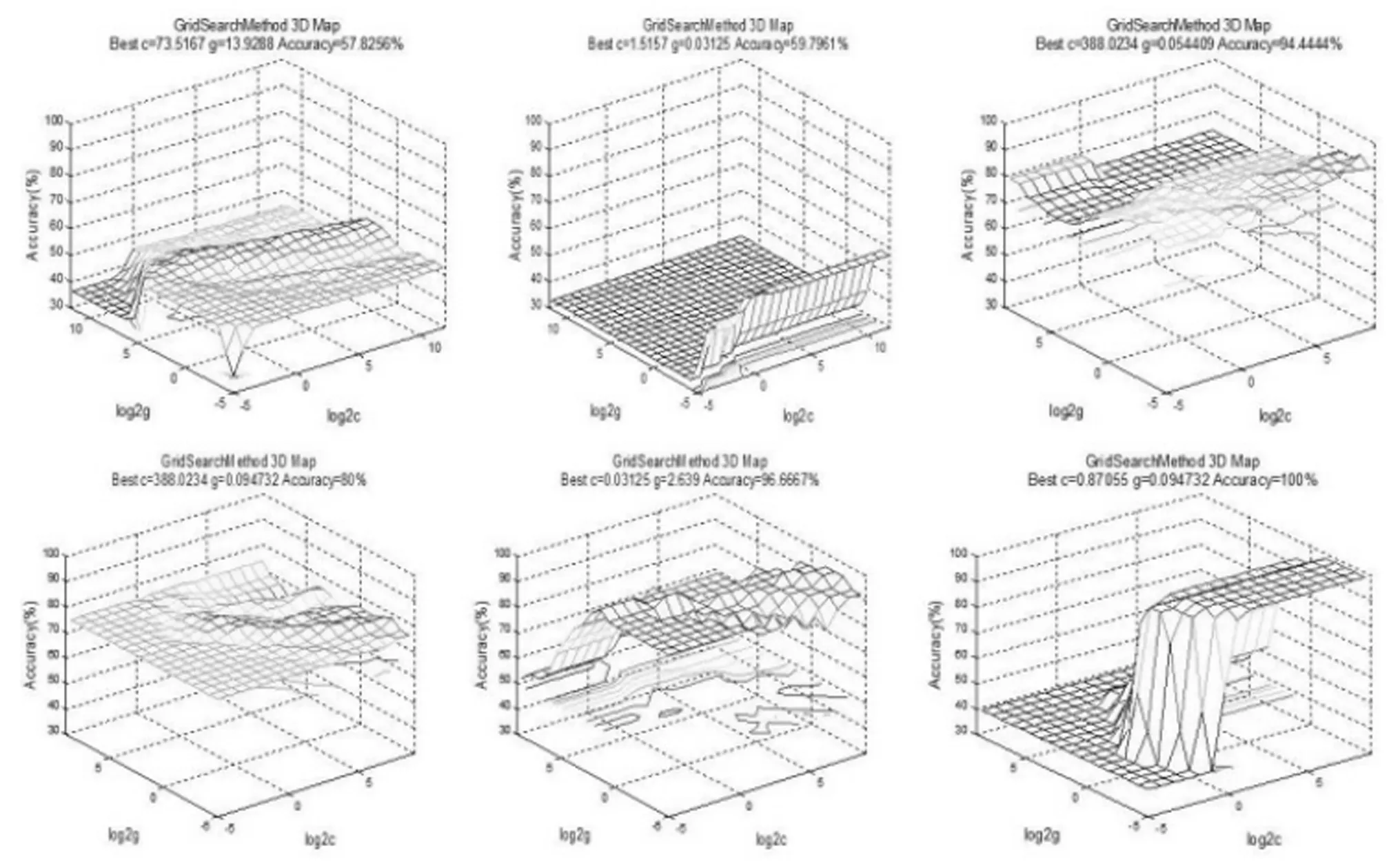
图4 网格法参数组的寻优过程

经验风险指训练样本的错误率，置信风险指测试样本的错误率。结构化风险为经验风险和置信风险之和。表2表明，网

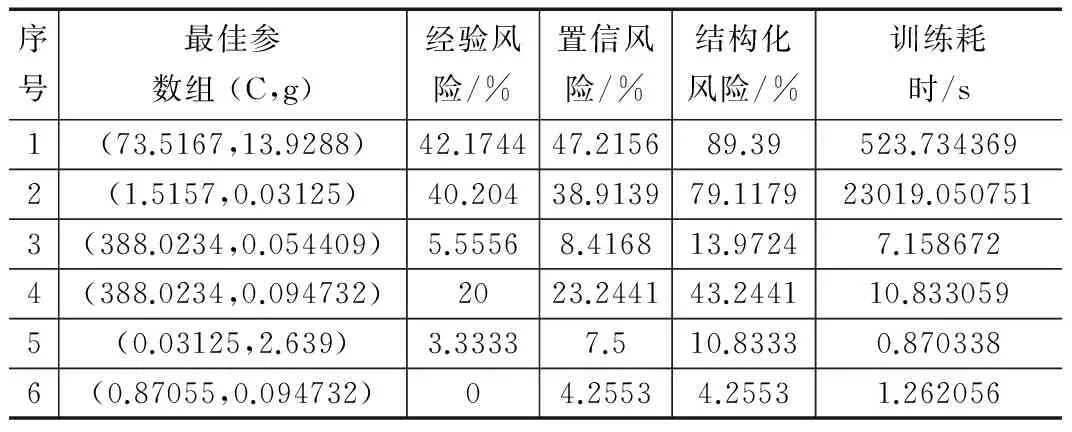
表2 网格算法参数寻优实验数据

格算法寻优的计算耗时与样本的个数、维数成正相关。数据集2有25 000个样本，训练时间长，且难以达到理想的效果。数据集2也说明置信风险不一定高于经验风险，即在训练过程中不能过度追求低经验风险，以结构化风险最小为原则，合理平衡经验风险和置信风险。综合6组实验，经验风险越低，获得的置信风险越低。

3.2 粒子群算法参数寻优

通过对生物系统和行为动态特征的观察与模拟，产生了较多的智能优化算法或称为启发式优化算法，包括遗传算法(genetic alogrithm, GA)、蚁群算法(ant colony opimization, ACO)、禁忌搜索算法(tabu search)、模拟退火算法(simulated annealing, SA)、粒子群算法(particle swarm optimization, PSO)等，其中遗传算法和粒子群算法较适用于组合优化问题[10-11]。应用粒子群算法进行支持向量机参数寻优，根据式(4)、(5)进行粒子i的第d维速度、位置更新。

(4)

(5)

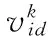
实验中粒子个体位置和速度都是二维向量，即(vi1,vi2)、(xi1,xi2)；速度惯性权重w=1；学习步长加速度常数c1=c2=1；种群变化的极值cmax=100,cmin=0.1,gmax=1 000,gmin=0.01。将预处理后的样本集进行粒子群算法参数寻优，寻优过程中采用三折交叉验证。利用PSO算法优化过程如图5所示，优化所得的结果如表3所示。

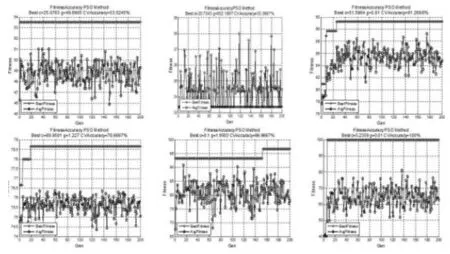
图5 粒子群算法参数寻优过程

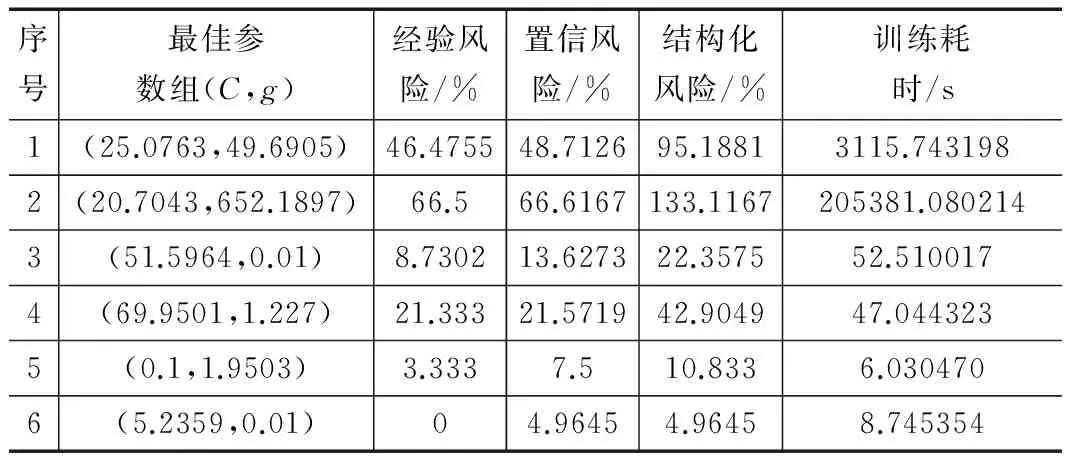
序号最佳参数组(C,g)经验风险/%置信风险/%结构化风险/%训练耗时/s1(25.0763,49.6905)46.475548.712695.18813115.7431982(20.7043,652.1897)66.566.6167133.1167205381.0802143(51.5964,0.01)8.730213.627322.357552.5100174(69.9501,1.227)21.33321.571942.904947.0443235(0.1,1.9503)3.3337.510.8336.0304706(5.2359,0.01)04.96454.96458.745354

实验结果表明，在粒子群寻优过程中，代数较小时，随着代数增加，平均拟合度逐步提升，个体趋于自我的最优状态，整体表现出较好的适应性。代数到达一定数值后，个体和群体的适应度更新缓慢，种群最佳适应度不再变化，个体最优解一致。说明粒子群算法在空间搜索时出现了停滞，容易陷入局部最优解。6组实验数据表明，随着样本数量的增加，粒子群算法收敛速度缓慢，算法的时间复杂度为O(n2)，受样本影响大。

3.3 遗传算法参数寻优

在寻优过程中，最优参数组具有不确定性，当穷举范围较大时，计算量的剧增为寻优带来更多不确定因素。对这类多项式复杂程度的非确定性问题(non-deterministic polynomial, NP)搜索方法中较有名的就是遗传算法(genetic algorithm, GA)[14]。此外该算法对适应度函数无解析性质要求，且可得到全局最优解。按照Dariwin进化论中生物进化过程设定种群，并对个体进行二进制或格雷码形式基因编码。根据设定的寻优目标，得到个体适应度，再经过基因选定父代，通过父代的交叉或变异，产生新个体，最终达到寻优的目的。该启发式搜索算法采用轮盘赌法(roulette wheel selection)，个体被选中的概率正比于适应度，逐步淘汰适应度低者。在由M个个体组成的群体中，设个体的适应度设为fi，对应的遗传给新一代的概率P(xi)如式(6)，累计概率qi如式(7)。

(6)

(7)

遗传算法的参数设置一般依据经验进行，不同的参数组合对其性能影响较大，其中种群个数、遗传代数、交叉率、变异率都会影响解空间搜索的深度和广度。本文根据以往经验设置种群规模pop=20，最大遗传代数为200。为保证个体在有限的区域进行最优解搜索，设定参数c的变化范围为[0,100]，参数g的变化范围为[0,1 000]，交叉率为0.9，变异率为0.1，编码长度为20，将预处理后的样本集进行遗传算法参数寻优，寻优过程中采用三折交叉验证。利用GA算法优化过程如图6所示，训练所得结果如表4。

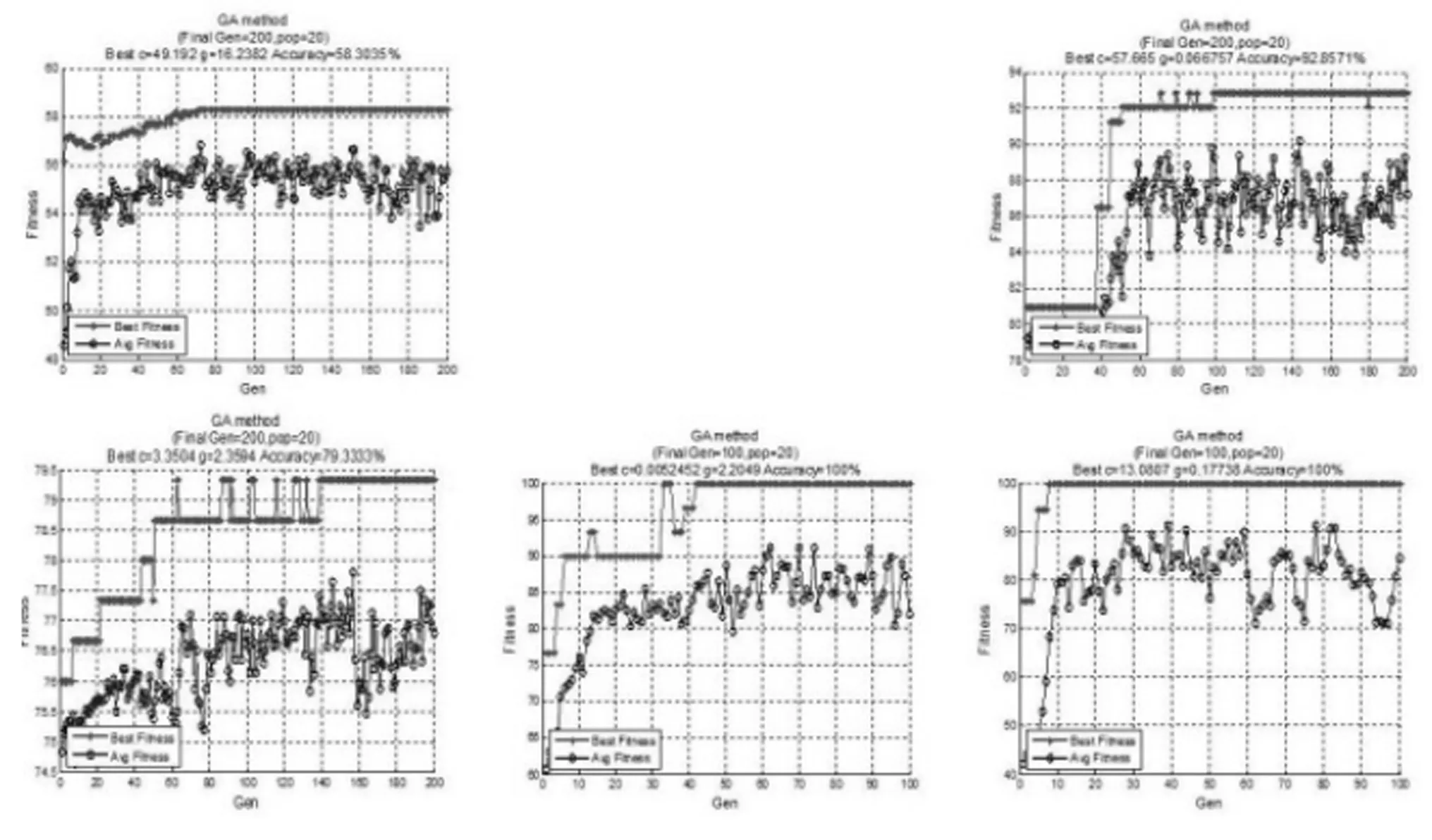
图6 遗传算法参数寻优过程

序号最佳参数组(C,g)经验风险/%置信风险/%结构化风险/%训练耗时/s1(11.5126,25.4269)41.696547.335389.03181964.5455452(*,*)****3(0.2944,2.1315)7.14298.617215.760137.3132134(2.5928,729.3432)21.333324.414745.74857.7599485(0.0052452,2.2049)07.57.52.3790516(6.288,0.15831)07.09227.09223.432706

由表4可看出在遗传算法中，随着代数的增加，遗传算法过程能实现优胜劣汰，收敛到全局最优解。实验中，数据集2在经历97小时的训练后仍未得到理想模型。数据集3的经验风险率低于置信风险率。大部分数据集在迭代20次后达到最优，但数据集5经过了62次迭代，表明GA的寻优能力受数据分布和规模影响。数据集2的寻优过程异常缓慢，其原因是算法中的随机变异和交叉率影响了个体的品质，在有限的进化代数中失去了寻优能力。以数据集6为例，遗传代数为3时达到了最优解，但因交叉和变异过程的进行，虽群体平均适应度逐步提升，但函数失去了收敛能力，只能依赖代数增加，逐渐收敛。故应适度的加入保护精英主义思想，保证当前最优解不参加变异，避免全局最优解被破坏。

3.4 实验分析

3.4.1 优化算法分析与应用策略

对比三种算法的最优解和寻优过程可知传统的迭代算法适用于小数据计算。数据量增大时，算法从设定的初始点开始，难以实现并行、网络计算，且因针对二维参数组寻优，算法复杂度为O(n2)，穷举过程时间频度高，计算效率低。网格算法的优点体现在对“坏数据”——数据集2的处理上，样本分类正确率比智能算法高30%。网格算法以时间和空间复杂度为代价，可以在规定的解空间内搜索到全局最优解，但精度严重依赖所设定的步长，解空间的设置依赖初始值的选取，故需在时间、精度以及空间做出权衡。

在SVM参数寻优过程中，PSO相较于GA，收敛时间较短但置信风险高，即快速收敛是以牺牲最优解的精度为代价。PSO实现较为简单，GA算法中既要保证种群的多样性，维持一定的交叉率和变异率，也要对适应度高的个体进行精英保护。本文所用的GA算法，对并行机制和网络反馈信息利用不充分，导致数据集5的收敛速度较慢。终止进化条件应灵活设置，避免数据集6在经验风险为0后，继续进化。

实验中，PSO和GA的算法复杂度分别为O(n^2)、O(log2n)。与传统的网格法比较，这两种智能算法表现出了极高的学习性能，有良好的全局搜索能力及并行性，可进行快速分布式计算。给定的参数组范围c=[0,100],g=[0,1 000]，计算次数远多于网格算法的225次，但耗时与网格算法相当。智能算法的缺陷是过分依赖初始化种群的规模、迭代次数及变异率等参数，且无严格的参数设置原则，严重依赖于经验。由于训练过程中的变异和选择过程具有随机性，实验结果难以重现。故在寻优过程中，可以使用智能算法进行最优解范围初步确定，以此确定解空间的初始值，再使用网格法进行高精度运算。

3.4.2 参数对SVM性能的影响

综合训练结果，训练样本对SVM的性能有较大的影响。数据集5、6分布均衡，个数适中，不同的优化算法都能得到较稳定的最优参数组合，得到较高的泛化机器。数据集3、4的数据分布不均匀，效果稍差。三种方法对数据集2的处理，都没有得到较理想的效果，且寻优时间长，过程缓慢，分析有以下三种原因：1)该数据的规模不适合选择支持向量机，应尝试神经网络、弱分类器级联等方法；2)高斯核函数对该数据不适用，可选择多项式核函数或二层神经收集核函数；3)本文直接进行了数学机械式归一化与降维，忽略了物理意义，应尝试针对特征向量的物理意义，做不同的预处理，以期达到理想的训练模型。

目标函数式(2)中训练样本误差项的惩罚系数C，控制着使分类间隔最大且错误率最小的折中，在确定的特征空间中调节学习机器的置信范围和经验风险的比例；而高斯函数的方差系数σ2，主要影响样本数据在高维特征空间中分布的复杂程度。通过网格算法可以看出，随着σ2的增大，分类效果会变差。但为追求最高适应度，使σ2不能减小超过临界点(即最优解)，否则带来严重的过拟合问题，使得经验风险概率与置信风险概率差距悬殊。实验数据也说明SVM有较高的独立性，针对不同的数据集，最优参数不同，不具有泛化性。

4 结语

本文利用传统和智能优化算法对 SVM应用过程中的核函数参数组(C,σ2)进行优化。在对原始数据进行归一化和降维后，分别采取了网格法、粒子群法和遗传算法实现参数组寻优过程，并分析了 (C,σ2)对SVM泛化性能的影响。在应用SVM时，为加快收敛速度、提高最优解精度，应采取优化算法混合的策略，利用智能算法进行初步最优解定位，然后采用网格算法进行高精度最优解的确定，可以得到性能较好的支持向量机模型。

[1] Vapnik V. The nature of statistical learning theory[M]. Springer Science & Business Media, 2013.

[2] Vapnik V N, Vapnik V. Statistical learning theory[M]. New York: Wiley, 1998.

[3] Chapelle O, Vapnik V, Bousquet O, et al. Choosing multiple parameters for support vector machines[J]. Machine learning, 2002, 46(1-3): 131-159.

[4] University of California-Irvine． UCI Machine Learning Repository.http://archive.ics.uci.edu/ml/datasets.html.2015-04-11.

[5] Eitrich T, Lang B. Parallel tuning of support vector machine learning parameters for large and unbalanced data sets[M].Springer Berlin Heidelberg, 2005: 253-264.

[6] He H, Garcia E A. Learning from imbalanced data[J]. Knowledge and Data Engineering, IEEE Transactions on, 2009, 21(9): 1263-1284.

[7] Zhang Z, Guo H. Research on Fault Diagnosis of Diesel Engine Based on PSO-SVM[A].Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation[C]. Atlantis Press, 2016: 509-517.

[8] Smits G F, Jordaan E M. Improved SVM regression using mixtures of kernels[A]. 2002. IJCNN'02.Proceedings of the 2002 International Joint Conference on IEEE[C]. 2002, 3: 2785-2790.

[9] Keerthi S S, Lin C J. Asymptotic behaviors of support vector machines with Gaussian kernel[J]. Neural computation, 2003, 15(7): 1667-1689.

[10] Duan S M, Mao J L, Li J L, et al. Design Implementation and Application of Swarm Intelligence Algorithm Optimization Function Simulation Platform[A].Software Engineering and Information Technology: Proceedings of the 2015 International Conference on Software Engineering and Information Technology (SEIT2015)[C]. 2016: 196-203.

[11] Yu S, Zhang J, Zheng S, et al. Provincial carbon intensity abatement potential estimation in China: a PSO-GA-optimized multi-factor environmental learning curve method[J]. Energy Policy, 2015, 77: 46-55.

[12] Shi Y, Eberhart R C. Empirical study of particle swarm optimization[A]. CEC 99.Proceedings of the 1999 Congress on Evolutionary Computation[C].IEEE, 1999, 3.

[13] Rao B J, Babu M S P. Ongole Breed Cattle Health Expert Advisory System Using Parallel Particle Swarm Optimization Algorithm[J]. 2014.

[14] Yang C, Xu X, Han J, et al. Energy efficiency-based device-to-device uplink resource allocation with multiple resource reusing[J]. Electronics Letters, 2015, 51(3): 293-294.

Analysis and Strategy for Parameter OptimizationMethodsof SVM

Guo Keyou, Guo Xiaoli, Wang Yiwei

(School of Material and Mechanical Engineering, Beijing Technology and Business University，Beijing 100048，China)

To selectparameters of support vector machine (SVM) during application, we choose sample sets from UCI database. TheparametersoptimizationofSVM with kernel function is achieved throughtraditional grid method, particle swarm optimization algorithmand genetic algorithm inintelligentoptimization algorithms. And the optimum parameters are applied to testingsamples. The kernel function optimization strategy is obtained after athorough analysis of the relationship between parameters, the influence of parameters on the performance of SVMand the pros and cons of both traditional and intelligent optimization algorithms. The users should use intelligent optimization algorithm preliminarily to make sure the scope ofparameters, and couple it with grid method to obtain a high degree of accuracy.Experimental datas verify the effectiveness of the strategy, which expandsthe generalization and application ofSVM.

support vector machine; kernel function; traditionaloptimization algorithms; intelligentoptimization algorithms

2016-03-24；

2016-04-21。

交通运输部信息化科技项目(2012-364-835-110)；北京工商大学科研能力计划项目。

郭克友(1975-) ，男，黑龙江省齐齐哈尔市人，博士，副教授，主要从事数字图像处理，模式识别，智能交通方向的研究。

1671-4598(2016)06-0255-05

10.16526/j.cnki.11-4762/tp.2016.06.070

TP391

A