模块化多电平变换器上、下桥臂不对称运行环流重复控制
2016-11-17赵争鸣袁立强
李 凯 赵争鸣 袁立强
模块化多电平变换器上、下桥臂不对称运行环流重复控制
李 凯 赵争鸣 袁立强
(电力系统及发电设备安全控制和仿真国家重点实验室(清华大学) 北京 100084)
模块化多电平变换器(MMC)以其模块化、可扩展和便于冗余容错设计等优势在高压直流输电等大功率场合得到了很多应用。然而,采用大量电力电子元器件使可靠性成为制约MMC发展的主要因素,而通过设置备用子模块进而实现容错运行成为提高其可靠性的主要手段。针对含备用子模块MMC发生子模块故障导致上、下桥臂不对称运行的情况,本文通过理论分析表明,环流中不仅包含了偶次谐波成分,还包含了不对称运行产生的奇次谐波成分。据此,本文采用改进的环流重复控制器,在实现MMC故障后容错运行的同时,还实现了对环流各次谐波成分的有效抑制。所提出的环流重复控制器,不仅适用于上、下桥臂不对称工况,也适用于对称工况。因此,故障前后无需进行控制器的切换,降低了容错控制的复杂度。本文通过搭建单相MMC硬件平台,验证了所提控制策略的有效性。
模块化多电平变换器 子模块故障 不对称运行 环流重复控制
0 引言
自从2001年德国Marquardt教授提出模块化多电平变换器(Modular Multilevel Converter, MMC)以来[1],学术界对其进行了大量的研究。与常规的中点钳位式和飞跨电容等多电平变换器相比,MMC以其模块化和可扩展等优势在高压大功率场合得到了越来越多的应用[2]。目前,MMC在高压直流输电(HVDC)和柔性交流输电系统(FACTS)中已经得到了工业应用。
MMC使用了大量的元器件,例如半导体开关器件和电容器等,而每个元器件都是潜在的故障因素,从而使可靠性成为应用MMC的主要挑战之一[3]。而MMC自身模块化的特点,使其易于设置备用,进而实现容错运行,这也是提高MMC可靠性的主要手段。针对MMC可靠性问题,现有文献对MMC的子模块备用策略和容错控制做出了很多研究。MMC设置备用子模块的策略主要包括有冷备用[4]和热备用[5-11]。冷备用策略指正常工作时备用子模块不投入运行,故障后启动备用子模块替换失效子模块。冷备用策略的控制较为复杂,而且故障后启动电容充电的过程,影响了暂态性能[6]。热备用策略指冗余子模块与其他子模块一样始终参与运行,虽然该策略增加了系统损耗,但是可以实现故障后的无缝切换,而且提高了备用子模块元器件的利用率。
热备用策略切除故障子模块的方案包括两种,一种是对称切除,即发生故障后,切除故障子模块的同时旁路故障相另一桥臂与故障子模块呈对称位置的子模块[8];另一种是不对称切除,即故障后只切除故障子模块。对称切除方案虽然保证了MMC故障后运行的对称性,但是降低了对备用子模块的利用率。不对称切除方案能够充分利用正常子模块,但是使故障后MMC上、下桥臂处于不对称运行的状态,从而带来基频环流和直流电流波动等问题[6,9-11]。为此,文献[6,10]提出了基于桥臂能量平衡的容错控制策略,通过改变故障后子模块电容电压,使得上、下桥臂的总能量维持平衡,从而有效地抑制了不对称运行引起的环流。但是,这种方法改变了故障桥臂子模块平均电容电压,故障后仍然存在电容充电的过渡过程。类似地,文献[11]引入了基频环流谐振控制,通过修正各桥臂投入导通的子模块个数来实现桥臂的能量平衡,进而解决不对称运行的问题,但是这种方法对高次的环流谐波并不能有效地抑制。
本文在对含热备用子模块MMC统一分析对称和不对称运行的环流成分基础之上,提出一种改进的环流重复控制策略,在实现故障容错运行的同时,还能对不对称运行各次环流谐波进行有效地抑制。本文通过实验,验证了所提控制策略的有效性。
1 含热备用子模块的MMC数学模型
以含热备用子模块的单相MMC为例来说明其数学模型,如图1所示,虚线框内代表了每桥臂的冗余子模块。MMC每桥臂包含有+个子模块,其中为额定子模块个数,为冗余子模块个数。这里的子模块可以为半桥子模块或全桥子模块。

(a)单相MMC
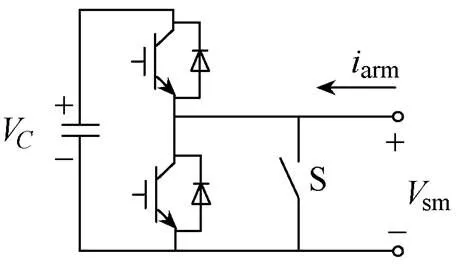
(b)半桥子模块
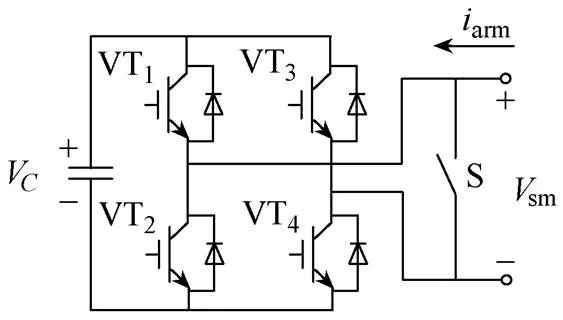
(c)全桥子模块
图1 含热备用子模块的单相模块化多电平变换器
Fig.1 Single-phase MMC with hot reserved SMs
在图1所示的MMC中,输出电流a、环流cira和上、下桥臂电流pa和na之间的关系为
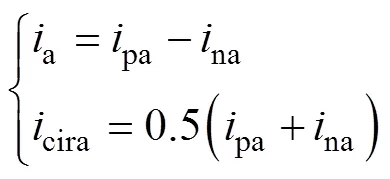
在推导环流谐波成分之前,首先假定MMC的实际输出电压和输出电流ao能完全跟踪参考值,并且将两者设定为
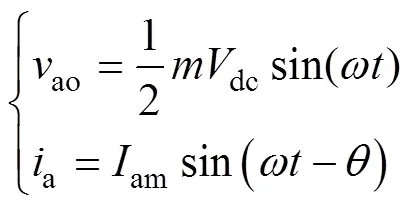
式中,为调制比;am为输出电流的幅值; 为角频率; 为输出电流滞后输出电压角度。
根据图1,经过推导可得上、下桥臂电压pa和na,即桥臂所有子模块输出电压之和,与输出电流和环流关系为

式中,arm为等效电阻,表征了桥臂损耗。在式(3)中,两个等式左边的电压分量分别决定了环流和输出电流的大小。通过控制这两个电压分量,可以实现对MMC输出电流和环流的控制。本文将式(3)左边的电压分量分别定义为环流电压cira和输出电动势a,即
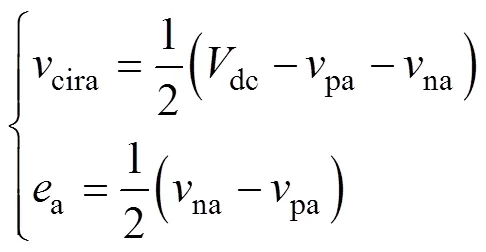
2 环流电压数学模型
本节对MMC上、下桥臂对称和不对称运行情况下的环流统一进行分析。由于MMC的环流电压决定了环流中的谐波成分,本节首先对桥臂电流的成分做出假设,然后推导出子模块充电电流、电容电压波动和桥臂电压的表达式,最终建立环流电压的数学模型。通过对环流电压的分析,确定了环流中的谐波成分。
根据式(1),可将上、下桥臂电流分别设为

式中,da为环流中的直流分量,即输入直流电流;zk为第次环流谐波分量。
由于MMC的损耗与实际输出有功功率相比很小,则可认为MMC的输入和输出有功功率是平衡的,从而可得输出电流幅值与da的关系为
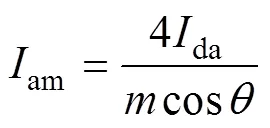
为了保证故障后的无缝切换,本文设定所有子模块平均电容电压始终为额定电压,即VN=dc/。通过文献[12]给出的三级电容电压平衡策略——平均电容电压控制、桥臂电容电压平衡控制和单个电容电压平衡控制,即可实现这一控制目标。
含热备用子模块MMC实际运行时,将上、下桥臂子模块个数分别设为+Fp和+Fn,其中p和n代表了上、下桥臂中因故障已经被切除的子模块数,则p≤、n≤。而每个子模块理论上是完全相同的,则采用直接调制[13]时,上、下桥臂每个子模块的平均开关方程为
根据式(5)的桥臂电流和式(7)的子模块平均开关方程,可得上、下桥臂子模块电容的平均充电电流ipa和ina分别为
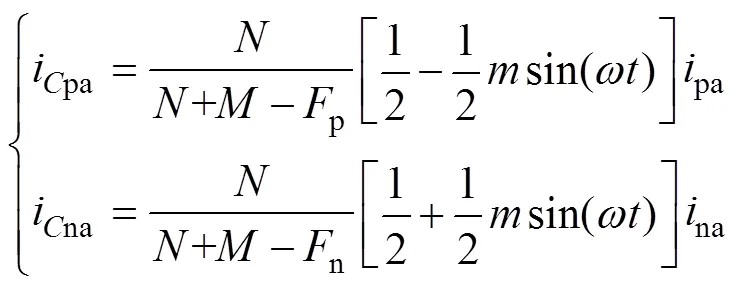
由式(8),则子模块电容电压波动可表示为
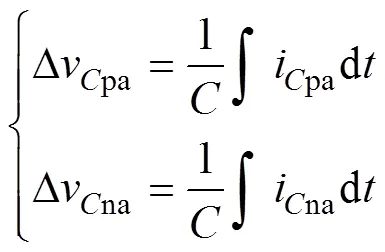
又考虑到子模块电容平均电压一直维持在额定电压dc/,则电容电压的实时值可以推导出。进而根据式(7)的子模块平均开关方程,可得上、下桥臂每个子模块的输出电压smpa和smna为
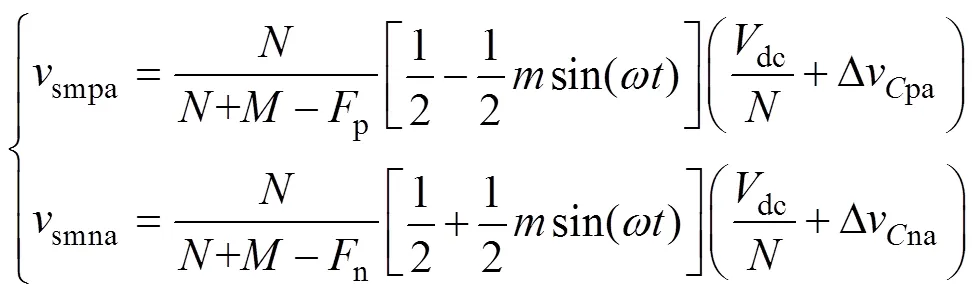
则上、下桥臂输出电压分别为

将式(5)、式(8)~式(11)代入式(4),又根据式(2)和式(6)给出的输出电流a和输入直流电流da的表达式,则可推导出环流电压cira的具体表达形式。为了简便表示上、下桥臂的不对称性,定义变量1和2为
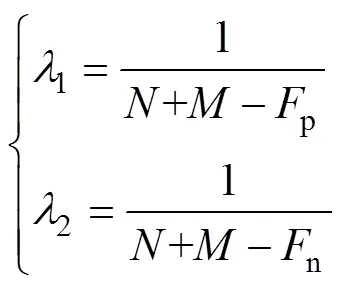
则环流电压可以用四部分表示为

式中,cira_1、cira_2、cira_3和cira_4的表达式为
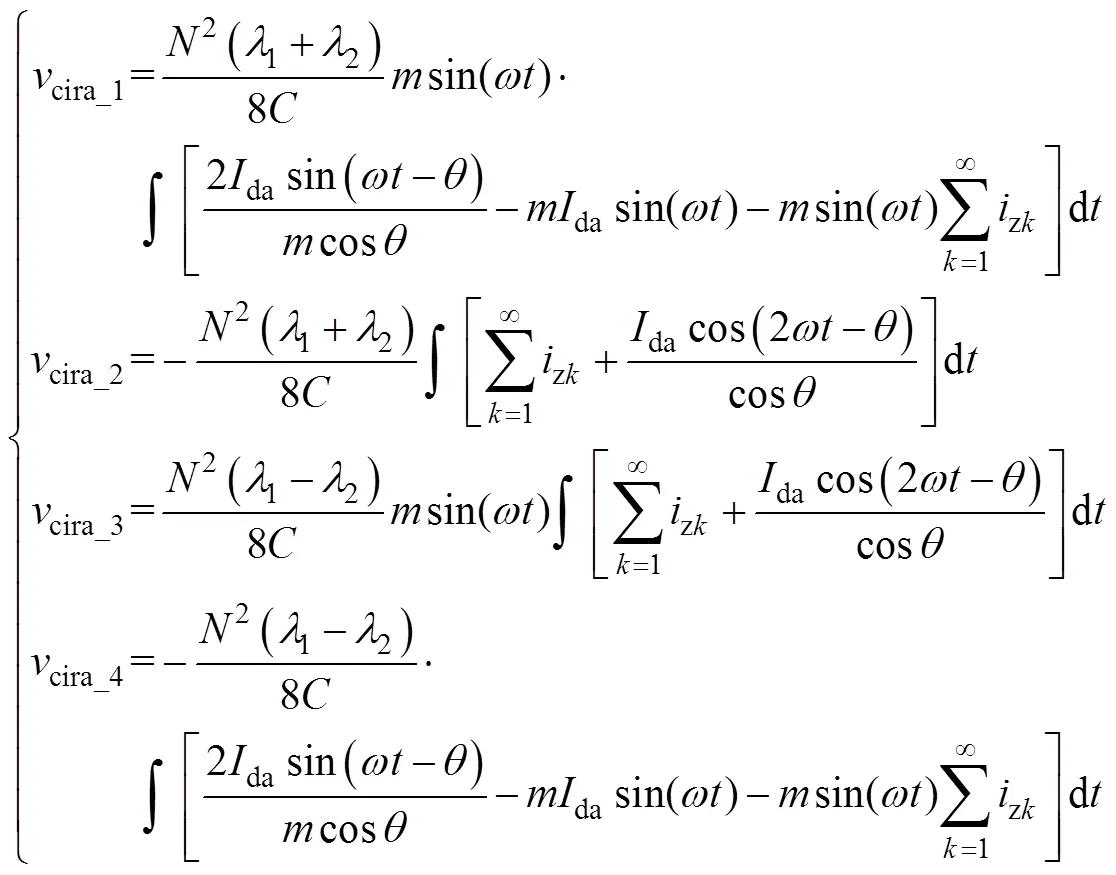
以下分对称和不对称运行两种情况,对式(14)中的四部分环流电压成分进行分析。
(1)首先分析上、下桥臂子模块个数相同的情况,此时1=2,则cira_3和cira_4都为零。分析cira_1的成分和cira_2中的下划线部分可知,环流电压中包含2次谐波分量。而由cira_1可知,次环流谐波分量需要和二倍频成分相乘,从而可得环流电压中包含-2和+2次谐波分量。由此,环流电压中的2次谐波分量会产生直流分量和4次谐波分量;进一步地,4次谐波分量又会引出6次谐波分量。迭代下去可得,对称运行时环流电压以及环流中包含2、4、6等各偶数次谐波分量。
(2)然后分析MMC上、下桥臂子模块个数不相同的情况,此时1≠2,环流电压中的四部分都不为零。由于备用子模块数-p和-n与额定子模块数相比较小,则1与2相差不大,1+2要比|12|大很多,所以cira_1和cira_2在环流电压中仍然是主要成分。根据前述分析可得,环流电压包含了偶次谐波分量以及2和+2次谐波分量。而对于cira_3,下划线所示的二倍频部分需要和一倍频成分相乘,则产生了一倍频和三倍频谐波分量;而cira_4自身就包含了一倍频分量;同时,在cira_3和cira_4中,次环流谐波分量需要和一倍频成分相乘,从而可得环流电压中包含了1和+1次谐波分量。综合以上分析可知,当1≠2时,不对称运行时环流电压以及环流中不仅包含2、4、6等偶数次谐波分量,同时也包含1、3、5等奇数次谐波分量。
常规的环流控制器只能对二次或者偶数次谐波进行抑制,对奇数次环流谐波并无作用。如果对这些奇数次环流谐波不加以控制,会引起直流侧电流波动,也会增加变换器损耗[10,11]。据此,本文对原有的环流重复控制器[14,15]进行改进,来统一抑制各次环流谐波。
3 不对称运行环流重复控制
重复控制是基于内模原理的一种控制思想,可用于消除信号中的周期性畸变[14]。根据第2节的分析可知,不管是否对称运行,环流中的谐波频率都为基频的整数倍,则采用重复控制器可对环流各次谐波进行有效抑制。
3.1 不对称运行环流重复控制器
针对MMC正常对称运行工况,文献[14]将PI控制器与重复控制器(Repetitive Controller, RC)结合起来,用于对偶数次环流谐波的抑制。而文献[15]指出RC自带积分控制器的效果,为了解决PI控制器和RC在设计的冲突,采用了P+RC形式的环流控制器。本文针对MMC故障后的不对称运行工况,沿用P+RC的环流控制器结构,如图2所示。其中,1/(arm+arm)为根据式(3)得到的环流模型传递函数。
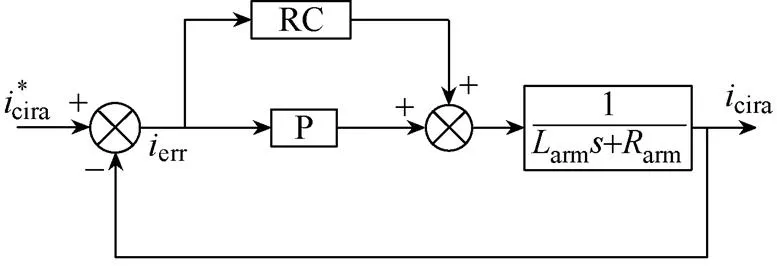
图2 MMC不对称运行环流重复控制结构
一般RC的连续域形式如图3a所示,()是为保证稳定性所设置的低通滤波器,()为补偿器,e-sT是为周期延迟环节。图3b为RC的离散域形式。
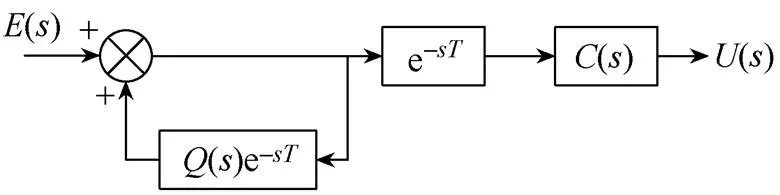
(a)连续域重复控制器

(b)离散域重复控制器
图3 重复控制器一般结构
Fig.3 General structure of the repetitive controller
由于重复控制算法一般是在DSP中实现,这里只考虑离散域RC的设计,给出低通滤波器、周期延迟环节和补偿器的形式为
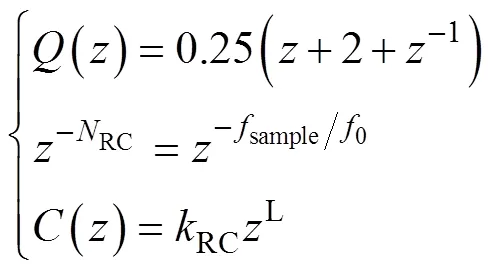
式中,()为零相移的滑动平均滤波器[15];RC为周期延迟的点数;sample为采样频率;0为工频频率;RC为补偿器()的增益,超前环节L是为了补偿实际DSP的计算延迟。由于不对称运行时环流最低次谐波为基频谐波,此时的RC取为一个基频周期内的采样点数。
图4给出了所设计P+RC控制器的开环传递函数伯德图,可看出控制器在50Hz、100Hz、150Hz等各谐波频率处都有很高的增益,即说明该控制器对奇数次和偶数次环流谐波都有很好的抑制效果。
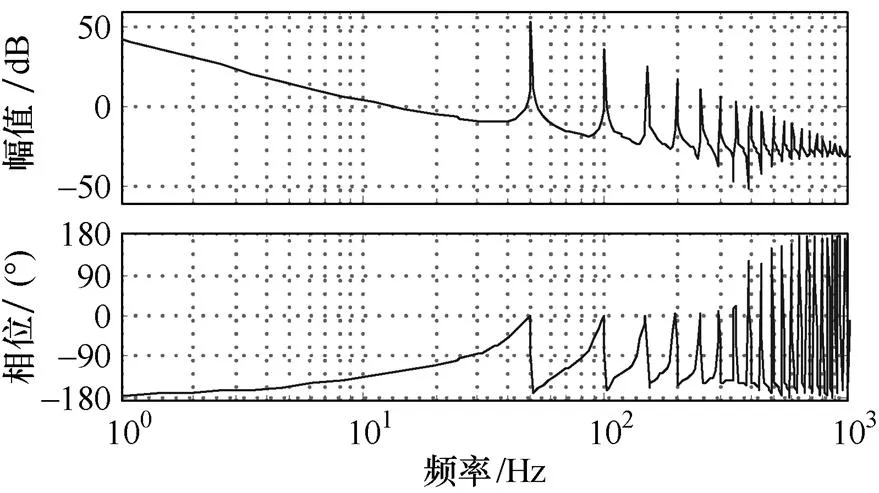
图4 P+RC环流控制器开环传递函数伯德图
3.2 MMC整体控制结构
本文采用的MMC整体控制结构如图5所示,包括输出电流控制、三级电容电压平衡控制[12]、P+RC环流控制、子模块参考波生成和载波移相调制等。
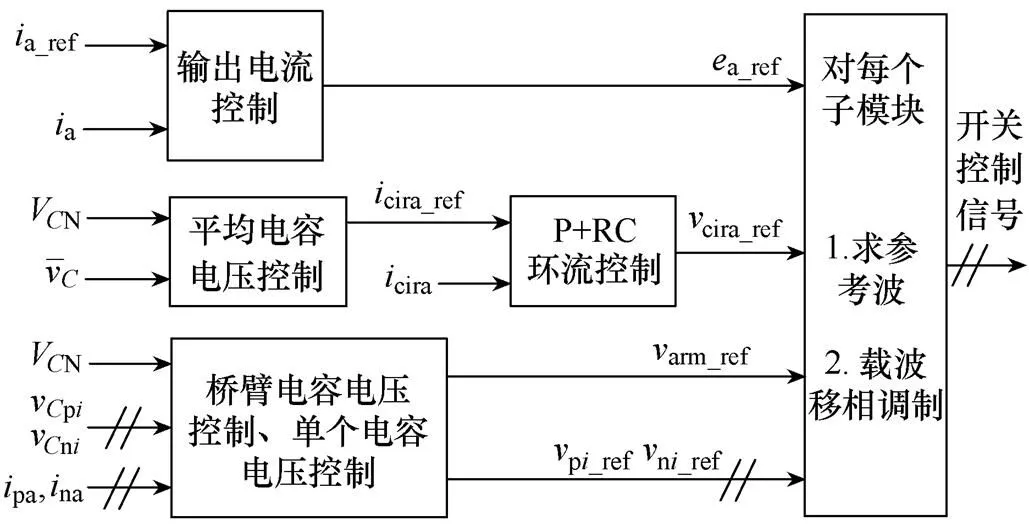
图5 MMC整体控制结构
图5中,电容电压的参考值始终设定为VN。最终上、下桥臂每个子模块的参考波分别为

式中,arm_ref为桥臂电容电压平衡控制分量;pi_ref、ni_ref为上、下桥臂各自电容电压平衡控制分量。
当发生子模块故障时,通过故障检测算法[16,17]检测、定位并切除故障子模块,同时更新p或者n,并且在平均电容电压控制和桥臂电容电压控制中将故障子模块剔除,即可实现故障后的无缝切换,同时抑制各次环流谐波。
4 实验验证
为了检验所提出的不对称运行环流重复控制策略,搭建了如图6所示的MMC硬件平台,参数见表1。硬件平台采用TMS320F28335的DSP作为控制器,用来执行控制算法和PWM信号的产生,同时采用型号为EP4CE15F17C8N的FPGA作为DSP控制器和各子模块之间的接口。硬件平台为采用全桥子模块的单相MMC,所得结论可扩展至采用半桥子模块的或者三相MMC。

图6 单相小功率MMC实验平台
表1 单相MMC小功率硬件平台参数
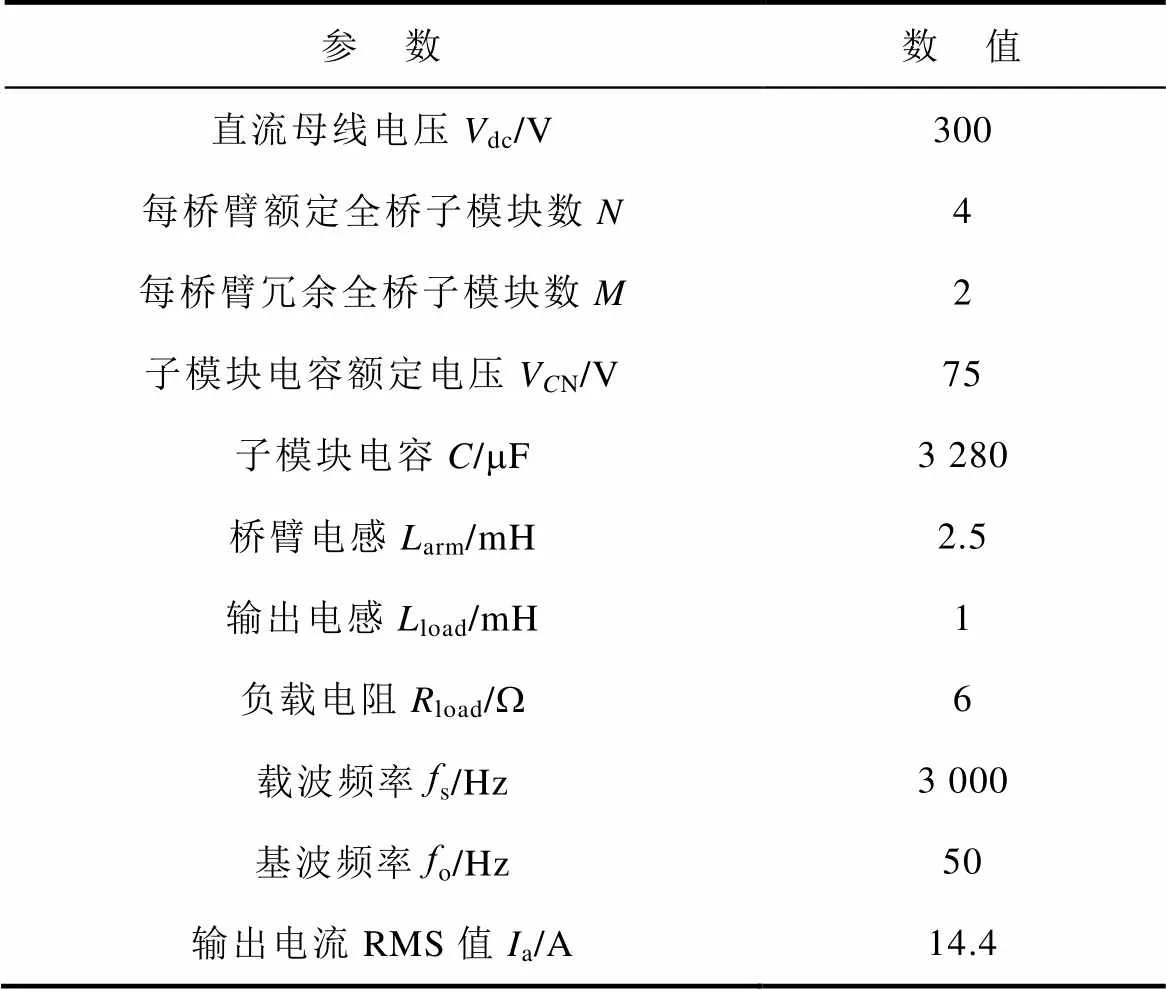
Tab.1 Parameters of downscaled MMC prototype
设置MMC不对称运行工况为上桥臂4个、下桥臂6个子模块同时运行,当采用原有用于正常对称工况的环流重复控制器时[15],MMC上、下桥臂电流和环流实验波形,以及环流FFT分析如图7所示。采用改进环流重复控制器的结果如图8所示。
通过比较图7和图8可知,对于不对称运行工况,原有重复控制器只能对2、4、6等偶数次环流谐波起到抑制作用,对1、3、5次环流谐波并无作用。而改进的重复控制器能有效抑制MMC不对称运行引起的各次环流谐波,并且将环流THD从18.86%降低到9.47%。
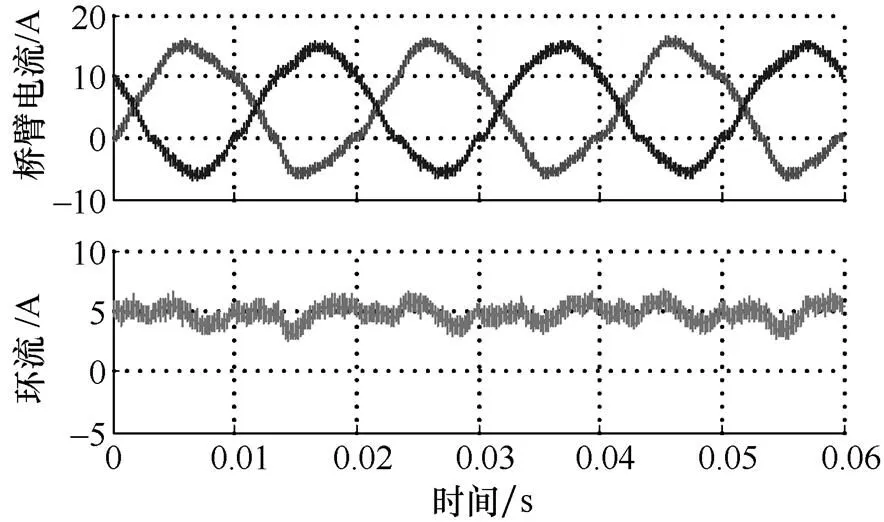
(a)上、下桥臂电流和环流实验波形

(b)环流实验波形FFT分析
图7 采用原有重复控制器的不对称运行环流实验波形
Fig.7 Circulating current waveforms under asymmetrical condition, with the traditional P+RC controller
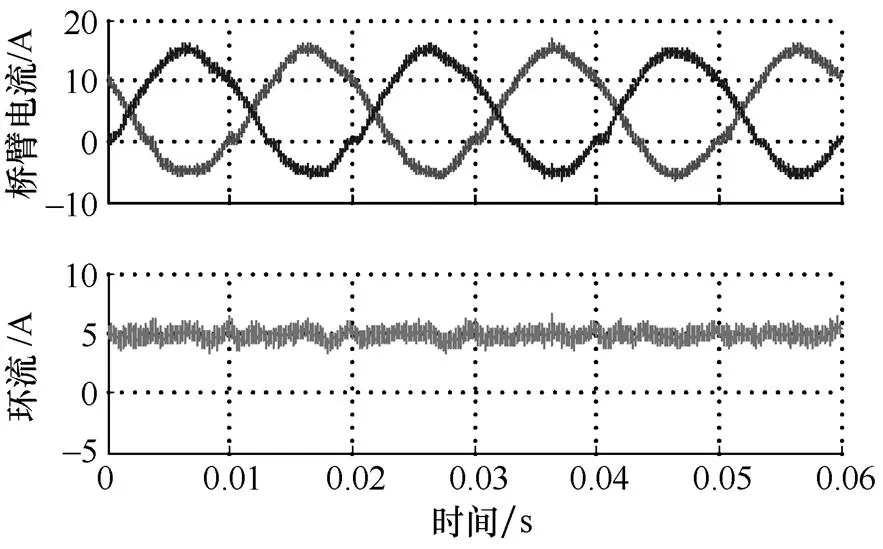
(a)上、下桥臂电流和环流实验波形
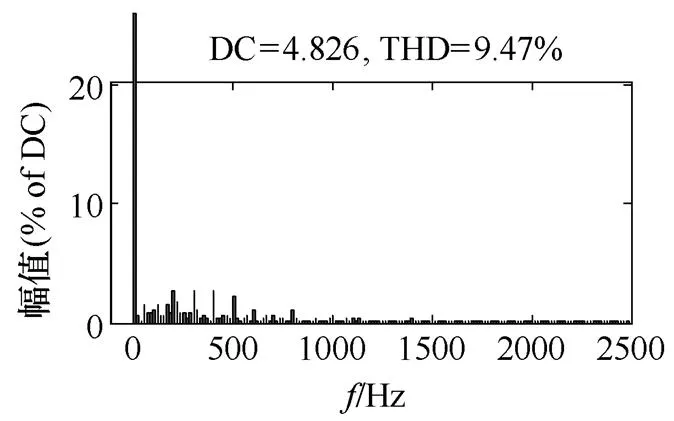
(b)环流实验波形FFT分析
图8 采用改进重复控制器的不对称运行环流实验波形
Fig.8 Circulating current waveforms under asymmetrical condition, with the improved P+RC controller
为了验证所提控制策略的故障容错效果,设置故障情景模式为:=0时刻,MMC正常工作,上、下桥臂各6个模块对称运行;=0时刻,上桥臂第三和第五两个子模块因故障被切除,上、下桥臂不对称运行。图9展示了故障容错过程的实验波形。
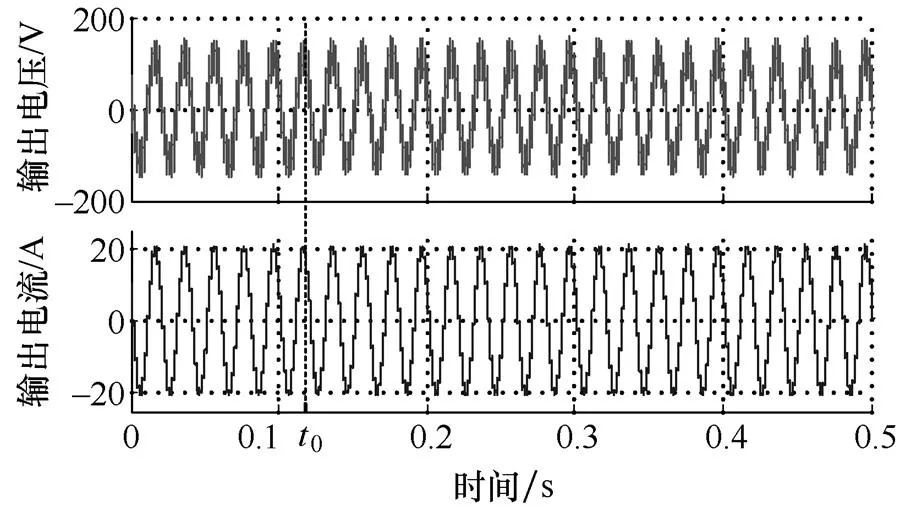
(a)输出电压和输出电流

(b)上、下桥臂电容电压
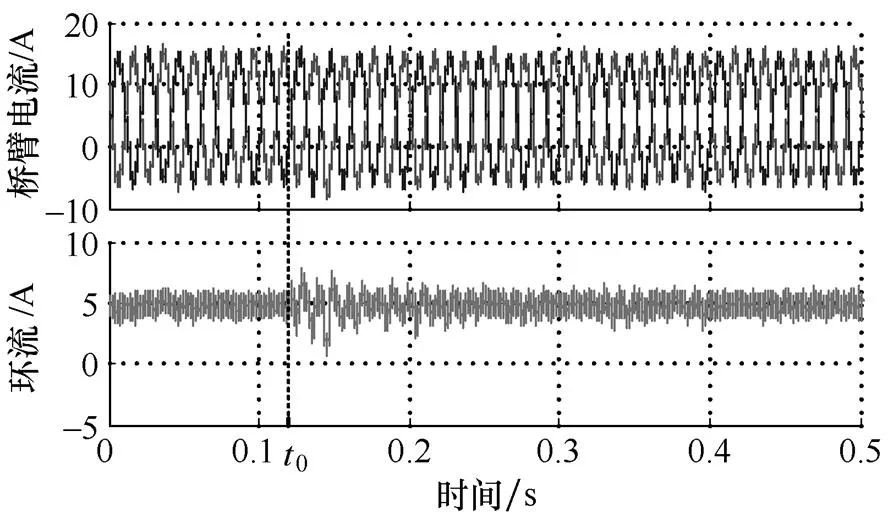
(c)上、下桥臂电流和环流实验波形
图9 MMC故障容错过程的实验波形
Fig.9 Waveforms of the fault-tolerant operation
在图9中,故障前、后的MMC输出电压和输出电流实验波形基本相同,说明不对称运行对输出影响不大。故障之后,被切除的故障子模块电容电压vp3和vp5不再波动,而其他正常子模块的电容平均电压仍维持在额定电压VN。故障之后的桥臂电流和环流经过短暂波动之后,又基本恢复到故障前情况。这些实验结果说明所提控制策略能够实现故障后无缝切换,并且不对称运行时的环流谐波得到了有效抑制。
5 结论
针对含热备用子模块的模块化多电平变换器发生结构性不对称故障时,即上、下桥臂子模块数不一致的情况,本文通过建立环流电压模型表明,环流中不仅含有2、4、6次等偶数次谐波,还含有1、3、5次等奇数次谐波。奇数次环流不仅增加了桥臂的器件损耗,还会对直流侧带来电流谐波。为此,本文提出改进的环流重复控制器,以实现MMC故障后的无缝切换,并且对不对称运行引起的奇数次环流谐波进行抑制。通过在单相MMC硬件平台上的实验结果,验证了所提出的不对称运行环流重复控制策略的有效性。
参考文献:
[1] Marquardt R. Stromrichterschaltungen mit verteilten energiespeichern: German patent DE, 20122 923U1[P]. 2001.
[2] Debnath S, Qin J, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.
[3] Deng F, Chen Z, Khan M R, et al. Fault detection and localization method for modular multilevel conver- ters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2721-2732.
[4] Li B, Zhang Y, Yang R, et al. Seamless transition control for modular multilevel converters when inserting a cold-reserve redundant submodule[J]. IEEE Transactions on Power Electronics, 2015, 30(8): 4052-4057.
[5] Gum T S, Hee-Jin L, Tae S N, et al. Design and control of a modular multilevel HVDC converter with redundant power modules for noninterruptible energy transfer[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1611-1619.
[6] Hu P, Jiang D, Zhou Y, et al. Energy-balancing control strategy for modular multilevel converters under submodule fault conditions[J]. IEEE Tran- sactions on Power Electronics, 2014, 29(9): 5021- 5030.
[7] Liu G, Xu Z, Xue Y, et al. Optimized control strategy based on dynamic redundancy for the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 339-348.
[8] 武文, 吴学智, 荆龙, 等. 模块化多电平变流器子模块故障容错控制策略[J]. 电网技术, 2016, 40(1): 11-18.
Wu Wen, Wu Xuezhi, Jing Long, et al. A fault- tolerated control strategy for sub-module faults of modular multilevel converters[J]. Power System Technology, 2016, 40(1): 11-18.
[9] 江丽丽, 马文忠, 李林欢, 等. 模块化多电平换流器的容错控制策略[J]. 电网技术, 2014, 38(9): 2497-2503.
Jiang Lili, Ma Wenzhong, Li Linhuan, et al. A fault- tolerant control strategy of modular multi-level converters[J]. Power System Technology, 2014, 38(9): 2497-2503.
[10] 马文忠, 江丽丽, 李林欢, 等. 模块化多电平变换器容错运行环流抑制策略[J]. 高电压技术, 2014, 40(11): 3513-3518.
Ma Wenzhong, Jiang Lili, Li Linhuan, et al. Circulating current suppressing strategy of modular multilevel converter in fault-tolerant control mode[J]. High Voltage Engineering, 2014, 40(11): 3513- 3518.
[11] 李探, 赵成勇. MMC子模块故障下桥臂不对称运行特性分析与故障容错控制[J]. 中国电机工程学报, 2015, 35(15): 3921-3928.
Li Tan, Zhao Chengyong. Operation characteristics of the MMC with asymmetrical arms under sub- module faults and the fault-tolerant control[J]. Proceedings of the CSEE, 2015, 35(15): 3921-3928.
[12] Hagiwara M, Maeda R, Akagi H. Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells (MMCC- DSCC)[J]. IEEE Transactions on Power Electronics, 2011, 26(6): 1649-1658.
[13] Song Q, Liu W, Li X, et al. A steady-state analysis method for a modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3702-3713.
[14] Zhang M, Huang L, Yao W, et al. Circulating harmonic current elimination of a CPS-PWM-based modular multilevel converter with a plug-in repetitive controller[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(4): 2083-2097.
[15] Li B, Xu D, Xu D. Circulating current harmonics suppression for modular multilevel converters based on repetitive control[J]. Journal of Power Electronics, 2014, 14(6): 1100-1108.
[16] Shao S, Wheeler P W, Clare J C, et al. Fault detection for modular multilevel converters based on sliding mode observer[J]. IEEE Transactions on Power Elec- tronics, 2013, 28(11): 4867-4872.
[17] 李探, 赵成勇, 李路遥, 等. MMC-HVDC子模块故障诊断与就地保护策略[J]. 中国电机工程学报, 2014, 34(10): 1641-1649.
Li Tan, Zhao Chengyong, Li Luyao, et al. Sub- module fault diagnosis and the local protection scheme for MMC-HVDC system[J]. Proceedings of the CSEE, 2014, 34(10): 1641-1649.
Repetitive Control of Circulating Current in MMC with Asymmetrical Operation of Upper and Lower Arms
(State Key Laboratory of Control and Simulation of Power Systems and Generation Equipments Tsinghua University Beijing 100084 China)
Due to the advantages of modularity, scalability and redundancy, modular multilevel converter (MMC) has been widely used in the high power applications such as HVDC transmission. However, the reliability becomes one of the most important challenges for MMC which is composed of a large number of power electronics components. To increase the reliability of MMC, the reserved sub-modules (SMs) are often utilized to realize the fault-tolerant operation. Considering MMC with the reserved SMs, the SM failures will cause the asymmetrical operation of the upper and the lower arms. Through detailed analysis in this paper, it can be concluded that there are not only even-order harmonics, but also odd-order harmonics in the circulating current under asymmetrical operation conditions. Accordingly, an improved repetitive controller of the circulating current is proposed in this paper, which guarantees not only the fault-tolerant operation of MMC, but also the suppression of all the harmonics in the circulating current. Whether MMC operates in the symmetrical or the asymmetrical condition, the repetitive controller can both work. Therefore, there is no need to switch controllers after the fault, which reduces the complexity of the fault-tolerant control. Experiments based on a downscaled single-phase MMC prototype have verified the effectiveness of the proposed control strategy.
Modular multilevel converter, sub-module failure, unsymmetrical operation, repetitive circulating current control
TM46
李 凯 男,1988年生,博士研究生,研究方向为面向可靠性的模块化多电平变换器的控制。
E-mail: kevinlee1988@126.com
赵争鸣 男,1959年生,教授,博士生导师,研究方向为大容量电力电子变换系统、光伏发电、电机控制等。
E-mail: zhaozm@tsinghua.edu.cn(通信作者)
2016-08-29 改稿日期 2016-09-18
国家自然科学基金重大项目资助(51490680、51490683)。
