无轴承异步电动机研究发展现状*

孙宇新， 杨玉伟

(江苏大学 电气信息工程学院，江苏 镇江 212013)



无轴承异步电动机研究发展现状*

孙宇新， 杨玉伟

(江苏大学 电气信息工程学院，江苏 镇江 212013)

无轴承异步电动机同时具备异步电动机的优良特性和磁轴承的特点，在航空航天、高速机械设备等领域具有非常广阔的应用前景。针对无轴承异步电动机的发展问题，国内外许多学者作了深入研究并取得了巨大进展。为了加强对无轴承异步电动机的研究，在叙述了无轴承异步电动机工作原理的基础上，详细综述了无轴承异步电动机近年来出现的具有代表性的结构设计、数学模型及控制方法。

无轴承异步电动机； 结构设计； 数学模型； 控制方法

0 引 言

传统的电动机使用机械轴承支承，转动时会产生机械摩擦，不但加大了电动机转子的摩擦力，磨损电机轴承，达到一定的磨损程度，还会产生机械振动，而且还会使支承轴承温度升高，加速轴承磨损，破坏润滑剂的性能，更糟糕的是会造成高速电机气隙不均匀，绕组产生热量，缩短电机及支承轴承的使用时间[1]。但是，随着社会发展，对高速及高性能电动机的需求越来越多[2]。2015年5月，国务院印发的《中国制造2025》将以高速电机为核心的高档数控机床等列为国家大力推动、重点突破的发展领域。高速电机技术首要需要解决电动机转子支承难题，由此，磁轴承应运而生。其具有无机械摩擦、无磨损等优点，已经应用于很多领域[3-4]，但是磁轴承的构造复杂、轴向径向占用空间大，且轴向空间的使用率较低，使得使用磁轴承支承的高速电机的转速与功率受到了影响[5-6]。

为了克服磁轴承的缺点，研究者发明了无轴承异步电动机，将产生径向悬浮力的线圈绕制在普通异步电动机定子槽中，两套线圈共同生成电动机所需的转矩和径向力，实现转子的旋转和稳定悬浮[7-9]。无轴承异步电动机具有结构紧凑简单、无摩擦、弱磁容易，可以高速和超高速运行等优点[10]。

本文阐述了无轴承异步电动机工作原理，并从电动机的结构设计、数学建模和控制方法角度详细介绍了无轴承异步电动机的研究发展现状。

1 无轴承异步电动机工作原理

无轴承异步电动机要想完成转子自悬浮，需要有控制径向力的线圈，则存在悬浮绕组和转矩绕组两套绕组，其极对数分别为p1和p2，电角频率分别为ω1和ω2。研究发现，当两套绕组满足p2=p1±1，ω1=ω2时，无轴承异步电动机就能依靠自身产生的可控旋转力和悬浮力使电动机实现转子有控旋转与可靠悬浮。

若是电机转子受外拉力作用离开了电机定子的轴心位置，那就会使得电动机磁通密度分布不匀称，此时麦克斯韦合力指向转子偏离方向，大小不为0。撤销外拉力之后，借助于固有的电磁力，转子没有办法恢复到原来位置。为了实现转子悬浮在定子中心，需要通过控制悬浮绕组来改变原来气隙中的磁场分布，通过可以控制的麦克斯韦力将转子拉回到定子中心。

2 无轴承异步电动机结构设计

2.1 二自由度无轴承异步电动机结构

无轴承异步电动机的结构设计目前主要集中在二自由度无轴承异步电动机，即在传统三相异步电动机的定子线圈槽中绕制一组控制径向悬浮力的线圈，转子结构没有改变。这种电动机结构简单，但控制比较复杂[11]。其结构如图1所示。

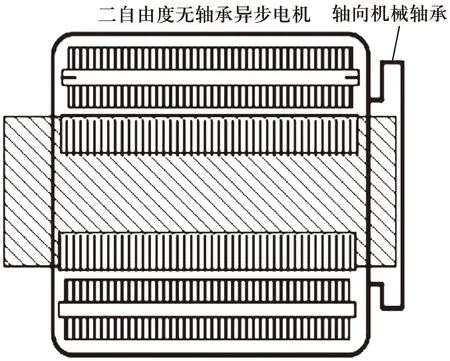
图1 二自由度无轴承异步电动机结构

目前大部分无轴承异步电动机采用双绕组定子结构，利用两个逆变器分别给两套线圈提供电流使得转子悬浮与旋转，其中要求两套线圈通过电流频率一致。但是双绕组结构的电动机体积大，功率损耗大，为此，文献[12]提出一种将定子每相线圈利用裂相式构造分成两部分的三相单绕组无轴承异步电动机。

2.2 四自由度无轴承异步电动机结构

文献[13]在二自由度无轴承异步电动机结构基础上，提出了一种四自由度无轴承异步电动机，结构如图2所示。

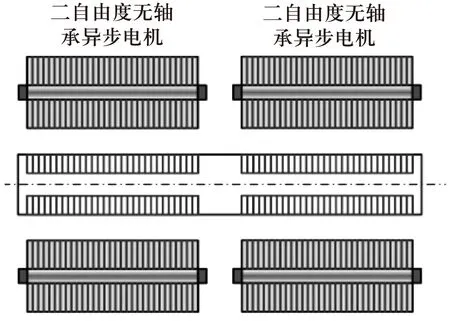
图2 四自由度无轴承异步电动机结构

该无轴承异步电动机左右两端的两个径向自由度分别由二自由度无轴承异步电动机控制。

2.3 五自由度无轴承异步电动机结构

为了弥补以上无轴承异步电动机存在的缺陷，将电动机真正应用到工程实际中，文献[14]提出了一种五自由度无轴承异步电动机。该电动机由2台二自由度无轴承异步电动机和1个轴向单自由度磁轴承构成。但是，该电动机结构复杂、体积大，2台电动机之间存在同步协调控制问题。针对这些不足，文献[15-16]提出了一种新型五自由度无轴承异步电动机，结构如图3所示。该电动机由交直流三自由度永磁偏磁交直流混合磁轴承和二自由度无轴承异步电动机结合，将旋转力和悬浮力磁路巧妙合二为一。

图3 五自由度无轴承异步电动机结构

3 无轴承异步电动机数学模型

3.1 径向悬浮力方程

现如今研究径向悬浮力主要使用虚位移法、麦克斯韦张量法两种方法。

3.1.1 虚位移法

文献[16-17]在分析电动机原理的基础上采用虚位移法来建立径向悬浮力表达式。

无轴承异步电动机的电感矩阵为

(1)

式中： L1s、L2s——转矩、悬浮两套绕组的自感；

x、y——无轴承异步电动机转轴的x轴、y轴位移；

M——两套绕组的互感系数。

无轴承异步电动机的线圈中存储的气隙磁场能量为

(2)

式中： i——电流矩阵，i=[i1sdi1sqi2sdi2sq]T；

i1sd、i1sq——转矩线圈电流的d、q轴分量；

i2sd、i2sq——悬浮线圈电流的d、q轴分量。

根据虚位移法的求解法则，电磁力可以通过电磁能量对位移变量求偏导得到，因而径向悬浮力沿x轴、y轴的表达式为

(3)

3.1.2 麦克斯韦张量法

文献[18-20]介绍了采用麦克斯韦张量法计算电动机的径向悬浮力。

首先，假设电动机的气隙磁密为B，那么计算作用在转子表面的麦克斯韦力。此处计算面积dA上的麦克斯韦力，如式(4)所示：

(4)

当p2=p1+1时，对式(4)进行积分运算获得x、y轴上麦克斯韦力分量为

(5)

式中： FM——麦克斯韦力幅值；

l——有效铁心长度；

r——电动机转子外径；

μ0——真空磁导率。

根据矢量运算法则，径向悬浮力在两相d-q坐标系下的表达式为

(6)

式中： kM——磁悬浮力系数；

ψ1d、ψ1q——气隙磁链在d、q轴上的分量；

N1、N2——转矩和悬浮绕组每组串联线圈的有效匝数。

文献[17，20-21]不仅研究了麦克斯韦力生成的使电动机转子悬浮的力，还研究了洛伦兹力生成的使电动机转子悬浮的力。由研究结果可知，洛伦兹力生成的使电动机转子悬浮的力远远小于麦克斯韦力生成的力，因此可以忽略不计。

文献[17，20，22]还分析了当转子偏离定子中心时，无轴承异步电动机中除了有可控的径向悬浮力外，还存在如式(7)所示的不可控的固有麦克斯韦力：

(7)

3.2 转矩方程

无轴承异步电动机中转矩和悬浮绕组电流生成的磁场分别在电机转轴上感应生成互相影响的感生电流，电磁转矩由其共同作用生成。但是，悬浮绕组磁场感生电流远远大于转矩绕组磁场感生的电流，可忽略[23-24]，由此得到在d-q旋转坐标系中的电磁转矩方程：

(8)

式中：L1m——转矩线圈互感；

Lr——转子自感；

ψ1rd、ψ1rq——转子磁链的d、q轴分量。

4 无轴承异步电动机控制方法

为了控制无轴承异步电动机以获得良好性能，研究人员对无轴承异步电动机控制方法进行了大量研究探索，并且取得了丰硕的成果。其控制方法主要有如下五大类。

4.1 磁场定向控制

磁场定向控制也称为矢量控制。其实质为控制电机的磁链矢量，人为将电机定子电流分解为转矩电流和磁场电流两个分量，实现静态解耦控制。磁场定向控制可分为三种： (1) 气隙磁场定向控制；(2) 转子磁场定向控制；(3) 定子磁场定向控制。文献[18，25-26]提出了基于气隙磁场定向的控制方法，控制系统如图4所示。

图4 基于气隙磁场定向的无轴承异步电动机控制系统

气隙磁场定向之后，气隙磁链分量变为ψ1d=ψ1，ψ1q=0。此时可得

(9)

径向悬浮力可简化为

(10)

此时可以通过控制流过转矩绕组和悬浮绕组的电流分别独立控制转矩和悬浮力。文献[27]针对气隙磁链矢量幅值及相位易受转子参数变化等因素影响的问题，利用通用磁场定向控制器控制无轴承电机。文献[28-29]针对由于转子电阻变化导致气隙磁场定向不准确的问题，提出了在线辨识转子电阻优化传统气隙磁场定向控制，取得了较好的控制效果。

为了进一步提高解耦效果，文献[30-31]采用了如图5所示的基于转子磁场定向的控制方法。

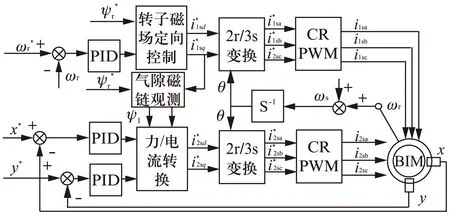
图5 基于转子磁场定向的无轴承异步电动机控制系统

转子磁场定向之后，转子磁链分量变为ψ1rd=ψ1r，ψ1rq=0。此时可得

(11)

则悬浮绕组电流为

(12)

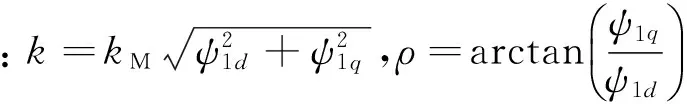
文献[32-33]在转子电阻会影响转子磁链观测大小的问题上提出了不含定转子电阻的转子磁链估计器，减少了转子参数对控制过程的作用。在转子磁场定向控制中，由悬浮绕组产生的转子电流通常被忽略，但该电流同样会改变径向悬浮力。文献[34]提出了一种新的转子磁场定向控制系统，该系统可以补偿径向悬浮力产生的延迟和方向误差。

为了达到控制系统对电动机本体参数依靠程度减弱的效果，文献[35-36]提出了基于定子磁场定向的控制方法。采用定子磁场定向之后，定子磁链分量变为ψ1sd=ψ1s，ψ1sq=0，则无轴承异步电动机的模型为

(13)

电机高速运行时，电磁转矩与悬浮力在定子磁链定向控制情况下实现了静态解耦，但低速情况下表现较为不足。文献[37]针对此缺点将U-I法和I-ω法相结合，组合成新观测方法获得定子、气隙磁通，取得较好效果。

4.2 直接转矩控制

针对磁场定向控制方法的不足，并且直接转矩控制(Direct Torque Control, DTC)策略已经在异步电动机上得到成功应用，学者们提出了无轴承异步电动机DTC方法。文献[38]针对传统DTC方法存在较大的输出转矩波动以及较大的电流谐波失真问题，研究了基于转矩磁链双PI控制器和空间矢量脉宽调制(Space Vector Pluse Width Modulation, SVPWM)的DTC方法。文献[39]在无轴承异步电动机SVM-DTC控制系统基础上，修正定子磁链同步角，使磁链与转矩控制环互相不影响，并且在试验中分析了占空比与输出电压谐波失真的联系，实现了占空比的设计，使其更加优越，约束了系统的转矩脉动和电流总谐波失真。文献[40]针对传统SVM-DTC系统中PID调节器无法解决快速与稳定之间的矛盾，采用自抗扰控制器替代PI或PID调节器，取得了较好效果。

4.3 悬浮系统独立控制

若能在线辨识转矩绕组生成的气隙磁场，即可实行无轴承异步电动机悬浮绕组的独立控制。由此，文献[41]提出使用电压模型法辨识得到气隙磁链，完成了无轴承异步电动机悬浮绕组的独立控制。

无论是应用电压传感器的电压模型法，还是应用霍尔元件或探测线圈法，都需要外加额外的器件或者增加电动机的复杂程度。文献[42]提出了一种新型气隙磁链辨识策略，根据逆变器开关状态，采用电压模型法辨识获得气隙磁场，实现悬浮绕组的独立控制。针对U-I模型气隙磁链辨识方法中存在纯积分从而会引入积分误差的问题，文献[43]提出了一种新的电动机磁链辨识积分方法，将带通滤波器和纯积分环节相串联，输入信号中的直流分量由带通滤波器滤除，又用信号无差通过滤波器进行积分算法，解决了存在纯积分环节问题。

文献[44]对独立控制方法进行了改进，使用静态神经网络建立悬浮绕组系统模型，最后基于逆控制器完成悬浮绕组的独立控制。此类独立控制方法不需辨识气隙磁链，不依靠转矩系统传递磁链信号，从而避免了各控制策略之间的相互制约问题。

4.4 非线性解耦控制

为了实现系统间的动态解耦，文献[16，45-46]将逆系统方法应用于无轴承异步电动机，对其进行了非线性动态解耦控制。系统如图6所示。首先利用数学模型推导出逆模型，结合逆模型将原系统解耦并得到4个相互独立的线性子系统，最后设计PI、PD控制器，实现转子磁链、转速，以及x方向和y方向上位移之间的非线性动态解耦。

图6 基于逆系统方法的无轴承异步电动机控制系统

文献[47]针对没有考虑转矩绕组定子电流动态特性的问题，在无轴承异步电动机的状态方程中加入了定子电流的动态部分，并在该状态方程下使用逆系统将无轴承异步电动机解耦成4个二阶线性积分子系统，此系统省去了电流闭环调节环节和负载转矩变量在线辨识环节。但是实际生活中系统的模型及逆模型很难求解得到，传统逆系统方法难以应用。由此，文献[48- 49]采用静态神经网络自适应得到电动机的逆模型，结合逆模型和原系统得到4个子系统，完成了基于神经网络逆的无轴承异步电动机解耦控制。神经网络的优点为能够自我学习和自适应未知的系统，但是存在局部极点小、过学习、运算量大等缺陷。文献[50]针对这些缺陷提出基于最小二乘支持向量机逆的无轴承异步电动机解耦控制，利用最小二乘支持向量机的非线性回归能力对样本做非线性回归，建立电动机的逆模型。文献[51]还提出使用非线性自适应滤波器建立正模型与逆模型的自适应逆解耦控制方法，利用非线性自适应滤波器离线训练速度较快，并且在建模过程中能解决各变量之间的耦合问题的特性，完成系统的动态解耦。

4.5 无传感器控制

要使无轴承异步电动机取得较好的控制效果必须获得转子转速和径向位移数据，因此速度位移传感器是必须的。但是，这些机械传感器不易安装、接线复杂、可靠性低，而且使得转子轴向长度变长，转子刚度降低，严重制约了无轴承异步电动机的性能，故必须研究无轴承异步电动机在没有传感器情况下的运行状况。

在无速度传感器方面，文献[36]提出了在线独立辨识转子和定子电阻，采用的方法为交互式模型参考自适应系统(Model Reference Adaptive System, MRAS)方法，实现了扰动较大情况下无速度传感器方式稳定运行。由于传统MRAS方法转速受积分环节影响，所以文献[52]提出一种基于转矩绕组无功功率的MRAS无速度传感器矢量控制方法，将瞬时无功功率作为一个可以调节的模型，建立转速与无功功率的关系式，实现对转速的在线辨识。针对使用MRAS方法获取转速信号的系统在低速时不稳定，文献[53]采用高频信号注入法实现了在电动机全速范围时转子速度和位置的检测；文献[54]利用扩展卡尔曼滤波器在线辨识转速变量实现无轴承异步电动机无速度传感器运行，而且还有效减少了计算量。

在无位移传感器方面，文献[55]在电动机数学模型的基础上得到转子径向位移观测器来实现转子径向位移的自我检测。文献[53，56]向悬浮线圈注入载波信号，检测该载波信号在悬浮线圈上产生的高频电压差分信号，实现转子在没有位移传感器的情况下运行。文献[57]向转矩线圈注入载波信号，检测该载波信号在悬浮绕组上产生的感应电压差分信号，使得电动机转子在没有位移传感器的情况下稳定运行。

5 结 语

本文叙述了无轴承异步电动机的概念和工作原理，重点分析了无轴承异步电动机的结构设计、数学模型的建立和控制方法等关键理论和技术。总体而言，经过近20年的研究和发展，无轴承异步电动机的结构设计、数学建模及控制的基本理论体系已经形成。无轴承异步电动机作为一种新型异步电动机，具有高效率、高稳定性、高速、无摩擦等特点，在飞轮储能、高速电主轴、先进制造及空调或冰箱用的离心式压缩机、生物工程用到的高速离心分离机等方面表现出特有的优势和较好的应用前景。

无轴承异步电动机是一种新型的无轴承电机，仍有一些技术需要研究：

(1) 无轴承异步电动机设计理论研究。目前无轴承异步电动机本体结构设计并没有一套成熟理论，因此总结并制定一套从设计、优化、动静态分析到样机制造、试验验证的设计理论十分重要。

(2) 精确数学模型研究。现有的机理建模方法是在忽略了电动机磁饱和、电动机发热引起的参数变化、变量谐波分量以及除气隙磁阻以外的其他磁阻及损耗的基础上建立的近似模型，而且无轴承异步电动机在不同工况下模型也是时变的，因此必须研究新的建模方法，充分考虑各种非线性因素，分析模型随参数的变化，建立精确的数学模型。

(3) 解耦控制方法研究。寻找一种解耦效果优越而且简单易实施，容易应用到实际控制中的解耦控制方法是今后的一个研究方向。

(4) 无传感器技术研究。高性能电动系统通常应用于精密加工等场合，通过传感器检测所需信号和信息不仅增加了系统成本，而且这些精密传感器发生故障会导致系统维护困难，影响了控制性能。因此研究无传感器技术是降低系统成本、提高系统稳定性的重要途径。

(5) 数字控制系统研究。无轴承异步电动机数字系统在高速实时性方面还面临挑战，不能适应高速、超高速运行的性能要求，需要结合可编程逻辑器件研究专用控制系统。

[1] 邓智泉,严仰光.无轴承交流电动机的基本理论和研究现状[J].电工技术学报,2000,15(2)： 29-35.

[2] 王桂香,徐龙祥,董继勇.高速磁悬浮电机的发热与冷却研究[J].中国机械工程,2010,21(8)： 912-917.

[3] 汪波,邓智泉,赵旭升,等.基于精确磁路的永磁偏置轴向径向磁轴承设计[J].中国机械工程,2012,23(17)： 2036-2041.

[4] 张剀,张小章.磁轴承不平衡控制技术的研究进展[J].中国机械工程,2010,21(8)： 897-903.

[5] BACHOVCHIN K D, HOBURG J F, POST R F. Stable levitation of a passive magnetic bearing[J]. IEEE Transactions on Magnetics, 2013,49(1)： 609-617.

[6] SCHUHMANN T, HOFMANN W, WERNER R. Improving operational performance of active magnetic bearing using kalman filter and state feedback control[J]. IEEE Transactions on Industrial Electronics, 2012,59(2)： 821-829.

[7] HENZEL M, FALKOWSKI K, ZOKOWSKI M. The analysis of the control system for the bearingless induction electric motor[J]. Journal of Vibroengineering, 2012,14(1)： 16-21.

[8] VICTOR V F, QUINTAES F O, LOPES J S B, et al. Analysis and study of a bearingless AC motor type divided winding, based on a conventional squirrel cage induction motor[J]. IEEE Transactions on Magnetics, 2012,48(11)： 3571-3574.

[9] 王正齐,刘贤兴,孙宇新.无轴承异步电机的非线性动态解耦控制[J].中国机械工程,2012,23(8)： 987-981.

[10] HIROMI T, KATOU T, CHIBA A, et al. A novel magnetic suspension-force compensation in bearingless induction-motor drive with squirrel-cage rotor[J]. IEEE Transactions on Industry Applications, 2007,43(1)： 66-76.

[11] CHIBA A, FURUICHI R, AIKAWA Y, et al. Stable operation of induction-type bearingless motors under loaded conditions[J]. IEEE Transactions on Industry Applications, 1997,33(4)： 919-924.

[12] FERREIRA J M S, ZUCCA M, SALAZAR A O, et al. Analysis of a bearingless machine with divided windings[J]. IEEE Transactions on Magnetics, 2005,41(10)： 3931-3933.

[13] CHIBA A, AKAMATSU D, FUKAO T, et al. An improved rotor resistance identification method for magnetic field regulation in bearingless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2008,55(2)： 852-860.

[14] SANTISTEBAN J, SALAZAR O, STEPHAN R, et al. A bearingless machine-an alternative approach[C]∥ 5th International Symposium on magnetic Bearings, Kanazawa, Japan, 1996： 345-349.

[15] SUN Y X, LIU X X, WANG W R, et al. Design and finite element analysis of high speed motorized spindle system based on bearingless induction motor[C]∥ 2010 International Conference on Mechanic Automation and Control Engineering， Wuhan, China, 2010： 5483-5486.

[16] ZHU H Q, ZHOU Y, LI T B, et al. Decoupling control of 5 degrees of freedom bearingless induction motors using α-th order inverse system method[J]. Acta Automatica Sinica, 2007,33(3)： 273-278.

[17] 王正齐.无轴承异步电机非线性解耦控制策略研究[D].镇江： 江苏大学,2011.

[18] 邓智泉,张宏全,王晓琳,等.基于气隙磁场定向的无轴承异步电机非线性解耦控制[J].电工技术学报,2002,17(6)： 19-24.

[19] UNGKU A U A, ASHER G M, SEWELL P, et al. Dynamic field modeling of torque and radial forces in vector-controlled induction machines with bearing relief[J]. IEEE Proceedings： Electric Power Applications, 2005,152(2)： 894-904.

[20] 杨泽斌.无轴承异步电机及其运行控制[D].镇江： 江苏大学,2013.

[21] 朱愰秋,沈玉祥,张腾超,等.无轴承异步电机数学模型与解耦控制[J].电机与控制学报,2007,11(4)： 321-325.

[22] 年珩,贺益康.感应型无轴承电机磁悬浮力解析模型及其反馈控制[J].中国电机工程学报,2003,23(11)： 139-144.

[23] 李华德.交流调速控制系统[M].北京： 电子工业出版社,2003.

[24] 陈伯时.电力拖动自动控制系统[M].北京： 机械工业出版社,2003.

[25] SUZUKI T, CHIBA A, RAHMAN M A, et al. Air-gap-flux-oriented vector controller for stable operation of bearingless induction motors[J]. IEEE Transactions on Industry Applications, 2000,36(4)： 1069-1076.

[26] 雷美珍,邱建琪,林瑞光.无轴承异步电机的悬浮机理及其气隙磁场定向控制[J].电机与控制应用,2005,32(7)： 35- 40.

[27] 贺益康,年珩,阮秉涛.感应型无轴承电机的优化气隙磁场定向控制[J].中国电机工程学报,2004,24(6)： 116-121.

[28] 郑静文,刘贤兴.无轴承异步电机气隙磁场定向的优化控制[J].电机与控制应用,2011,38(6)： 15-20.

[29] LIU X X, ZHU B, ZHENG J W, et al. Air-gap-flux oriented optimized control of bearingless induction motor[C]∥ Proceedings of the 30th Chinese Control Conference, Yantai, China, 2011： 3549-3553.

[30] SCHOEB R, BICHSEL J. Vector control of the bearingless motor[C]∥ 4th International Symposium on Magnetic Bearings， ETHZurich, Switzerland, 1994： 327-332.

[31] 邓智泉,王晓琳,张宏全,等.无轴承异步电机的转子磁场定向控制[J].中国电机工程学报,2003,23(3)： 89-92.

[32] 王少杰,卜文绍,翟利利,等.无轴承异步电机的定子电流矢量定向转子磁链估计[J].微电机,2012,45(8)： 14-17.

[33] BU W S, WANG S J, ZU C L, et al. Rotor flux estimation method of bearingless induction motor based on stator current vector orientation[C]∥ IEEE International Conference on Automation and Logistics， Zhengzhou, China, 2012： 437- 441.

[34] WANG Z Q, LIU X X. An improved rotor flux oriented control system of bearingless induction motors[C]∥2010 Chinese Control and Decision Conference， Xuzhou, China, 2010： 2733-2737.

[35] 于焰均,刘贤兴.无轴承异步电机定子磁场定向控制的研究[J].电气自动化,2009,31(3)： 20-22.

[36] 高剑,黄守道,马晓枫,等.基于交互式MRAS策略的无轴承异步电机无速度传感器矢量控制系统[J].电工技术学报,2008,23(11)： 41- 46.

[37] 黄守道,蔡国洋,高剑.无轴承异步电机的定子磁场定向解耦控制[J].湖南大学学报(自然科学版),2007,34(5)： 34-38.

[38] 刘贤兴,马桂芳,任海涛,等.无轴承异步电机SVM-DTC系统研究[J].传感器与微系统,2008,27(12)： 39- 42.

[39] 王宇,邓智泉,王晓琳.无轴承异步电机的直接转矩控制技术研究[J].中国电机工程学报,2008,28(21)： 80-84.

[40] 朱大敏,刘贤兴.基于自抗扰技术的无轴承异步电动机SVM-DTC控制系统[J].微特电机,2010,43(11)： 54-57.

[41] 邓智泉,王晓琳,李冰,等.无轴承异步电机悬浮子系统独立控制的研究[J].中国电机工程学报,2003,23(9)： 107-111.

[42] 张宏全,王晓琳,邓智泉,等.基于逆变器开关状态的无轴承异步电机悬浮系统独立控制[J].南京航空航天大学学报,2004,36(5)： 606-609.

[43] 周远平.无轴承异步电机悬浮子系统独立控制的研究[D].南京： 南京航空航天大学,2005.

[44] 孙晓东,朱愰秋,张涛,等.无轴承异步电机径向位置的动态解耦控制[J].控制工程,2010,17(2)： 224-227.

[45] 刘贤兴,董磊,范文进,等.五自由度无轴承异步电机的α阶逆系统解耦控制[C]∥第26届中国控制会议.张家界,中国,2007： 262-266.

[46] BU W S, LU C X, ZU C L, et al. Research on dynamic decoupling control method of three-phase bearingless induction motor[J]. International Journal of Control and Automation, 2014,7(5)： 77-86.

[47] 卜文绍,祖从林,路春晓.考虑电流动态的无轴承异步电机解耦控制策略[J].控制理论与应用,2014,31(11)： 1561-1567.

[48] SUN X D, ZHU H Q. Artificial neural networks inverse control of 5 degrees of freedom bearingless induction motor[J]. International Journal of Modeling, Identification and Control, 2012,15(3)： 156-163.

[49] 王正齐,刘贤兴.基于神经网络逆系统的无轴承异步电机非线性内模控制[J].自动化学报,2013,39(4)： 433- 439.

[50] 杨泽斌,孙晓东,张新华,等.无轴承异步电机最小二乘支持向量机逆解耦控制[J].江苏大学学报(自然科学版),2013,34(2)： 184-189.

[51] 孙宇新,杨玉伟,朱愰秋,等.基于非线性滤波器的无轴承异步电机自适应逆解耦控制方法： CN201510093203.4[P].2015-07- 08.

[52] 杨泽斌,汪明涛,孙晓东.基于转矩绕组无功功率MRAS的无轴承异步电机无速度传感器矢量控制系统[J].四川大学学报(工程科学版),2014,46(2)： 140-146.

[53] 马桂芳.无轴承异步电机无速度传感器技术的研究[D].镇江： 江苏大学,2009.

[54] 杨泽斌,樊荣,孙晓东,等.基于EKF的无轴承异步电机无速度传感器控制[J].仪器仪表学报,2015,36(5)： 1023-1030.

[55] MIZUNO T, ARAKI K, BLEULER H. Stability analysis of self-sensing magnetic bearing controllers[J]. IEEE Transactions on Control Systems Technology, 1996,4(5)： 572-579.

[56] KUWAJIMA T, NOBE T, EBARA K, et al. An estimation of the rotor displacements of bearingless motors based on a high frequency equivalent circuit[C]∥ Proceedings of the International Conference on Power Electronics and Drive Systems, Bandung, Indonesia, 2001： 725-731.

[57] TERA T, YAMAUCHI Y, CHIBA A, et al. Performances of bearingless and sensorless induction motor drive based on mutual inductances and rotor displacements estimation[J]. IEEE Transactions on Industrial Electronics, 2006,53(1)： 187-194.

Research and Development Status of Bearingless Asynchronous Motor*

SUNYuxin,YANGYuwei

(College of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

The bearingless asynchronous motor has the excellent characteristics of asynchronous motor and the features of magnetic bearing, and has very broad development prospects in aerospace and high speed mechanical equipment fields. On account of the problem about the development of bearingless asynchronous motor, thorough research had been made by many domestic and foreign scholars, and gigantic progress had been made. In order to strengthen the research of bearingless asynchronous motor, the working principle of the bearingless asynchronous motor was introduced, and the representative structure design, mathematical model and control method of the bearingless asynchronous motor in recent years were overviewed.

bearingless asynchronous motor; structure design; mathematical model; control method

国家自然科学基金资助项目(61174055)

孙宇新(1968—)，女，硕士研究生，副教授，研究方向为电力电子与电力传动。

杨玉伟(1990—)，男，硕士研究生，研究方向为电机解耦控制。

TM 359.9

A

1673-6540(2016)10- 0001- 08

2016-06-25