基于滑模观测器的无轴承永磁同步电机无速度传感器矢量控制*

陶 涛， 唐明军， 花良浩， 周 杰， 吕志香

(扬州工业职业技术学院 电气与信息工程学院，江苏 扬州 225127)



基于滑模观测器的无轴承永磁同步电机无速度传感器矢量控制*

陶 涛， 唐明军， 花良浩， 周 杰， 吕志香

(扬州工业职业技术学院 电气与信息工程学院，江苏 扬州 225127)

为解决无轴承永磁同步电机矢量控制系统中传统机械式传感器带来的成本及可靠性等问题，将滑模观测器技术应用到其控制系统中。该系统采用滑模面及滑模等效控制方法，并基于转矩绕组观测电流和其实测电流差值构建滑模面，观测电机反电动势，从而实现转子位置角及转速的精确估算。利用MATLAB仿真软件构建了无速度传感器运行仿真系统，对电机转速、转角信号进行辨识。仿真结果表明： 滑模观测器的转角、转速信号辨识精度较高，并能满足无轴承永磁同步电机无速度传感方式的稳定悬浮运行要求。

无轴承永磁同步电机； 滑模观测器； 速度自检测； 转角自检测

0 引 言

无轴承永磁同步电机(Bearingless Permanent Magnet Synchronous Motor, BPMSM)是一种结合了磁悬浮技术并集永磁同步电机优良特性于一体的新型电机。因此，其既具有永磁同步电机固有特征： 高功率、高能量密度、高功率因数；同时兼具磁悬浮轴承优异性能： 无摩擦、无需润滑、免维护、寿命长。因此，其可实现高速及超高速运行，是高速电机传动领域里的一项重大突破[1-2]。

基于转子磁场定向的解耦算法可实现径向悬浮力和转矩的独立控制，转子磁场定向控制需要能获得精确的转角、转速信号，从而获得磁场定向所需磁通的位置，进而实现转矩和径向悬浮力解耦控制，最终满足BPMSM稳定悬浮运行要求。传统BPMSM矢量控制系统中位置/转速信号均采用机械式传感器测量，而机械式传感器的安装与使用不仅使电机体积、成本增加，可靠性降低，更严重限制了BPMSM高速优良性能的发挥。因此，BPMSM无速度传感器技术因其具有重要的现实意义和广阔的应用前景，从而成为当前及未来的研究热点[3-6]。

国内外学者针对电机无速度传感技术提出了很多控制方法，大体可以分为三类[7-12]： 一类是基于电机理想模型的开环计算方法，如直接计算法、基于电感变化的估算法及反电动势积分法等，这类方法计算过程简单，在电机参数正确的前提下能够得到较为准确的转子位置估算结果，开环计算的方法原理简单，动态响应较快，但是这类方法极易受参数变化影响，算法不稳定。另一类是基于各种观测器模型的闭环算法，当前应用较为广泛的有扩展卡尔曼滤波器、滑模观测器、模型参考自适应算法及其他自适应算法等，电机无速度传感器控制在速度观测精度和系统的稳定性上都有了很大的提高。最后一类是以高频注入法为典型代表的基于电机非理想特性的算法，利用凸极机自身的凸极特性或者在高频信号下隐极机所表现出来的凸极特性，来估算电机转子位置和转速，为无位置传感器在极低速下的应用提供了新的思路。

本文通过借鉴传统永磁电机无速度传感器检测方法，提出基于滑模观测器的BPMSM无速度传感器矢量控制系统。通过在转矩绕组观测电流和其实测电流的误差上构建滑模面，观测电机反电动势，从而实现转子位置角及转速的精确估算。仿真结果表明： 滑模观测器的转角、转速信号辨识精度较高，并能满足BPMSM无速度传感方式的稳定悬浮运行要求。

1 BPMSM数学模型

BPMSM径向悬浮力产生的实质是由于悬浮力绕组所产生的磁场打破了原有转矩绕组所建立的气隙磁场平衡，从而产生作用在转子表面的径向悬浮力。将转矩绕组极对数数值大小设为pM，悬浮力绕组极对数数值大小设为pB，理论分析与试验结果均有力地证明了无轴承电机若需实现正常运行和稳定悬浮功能，必须满足以下三个条件，缺一不可： (1)pB=pM±1；(2) 两磁场旋转方向相同；(3) 产生旋转磁场的电流电角频率一致。

为了更为清晰地描述本文所建立的数学模型，现定义相关参数变量。定义ψM、ψB、ψPM分别为转矩绕组磁链、悬浮力绕组磁链、转子永磁体产生的磁链，ψMd、ψMq、ψBd、ψBq为相应绕组磁链直轴、交轴分量；iM、iB分别为转矩绕组电流、悬浮力绕组电流，iMd、iMq、iBd、iBq为相应绕组电流在直轴、交轴上的分量。

当转矩绕组极对数pM与悬浮力绕组极对数pB均≥2且满足pB=pM±1时，转矩绕组磁链ψM与悬浮力绕组磁链ψB之间没有相互交链。由于本文采用的是表贴式BPMSM，对于转矩绕组，有LMd=LMq=LM；对于悬浮力绕组，有LBd=LBq=LB。因此，当转矩绕组极对数pM与悬浮力绕组极对数pB均≥2且满足pB=pM±1时，BPMSM的转矩绕组与悬浮力绕组磁链方程分别为

(1)

(2)

当电机稳定运行，且转子稳定悬浮时，转矩绕组与悬浮力绕组电压方程分别为

(3)

(4)

式中：RM——两相旋转坐标系下的转矩绕组电阻；

RB——两相旋转坐标系下的悬浮力绕组电阻；

ω——同步旋转机械角速度。

对于表贴式BPMSM，当转子处于中心位置时，BPMSM的电磁转矩表达式应与普通永磁同步电机的电磁转矩表达式一致，即：

(5)

BPMSM转子受到的径向力包括三部分： 转子在电机气隙磁场中受到的麦克斯韦力构成的径向力；载流转矩绕组在悬浮力绕组气隙磁场中受到的洛仑兹力，与载流悬浮力绕组在转矩绕组气隙磁场中受到的洛仑兹力的作用于转子的反作用力构成的径向力；由于转子偏心引起气隙磁场分布不均而产生的径向力。所以BPMSM的径向悬浮力为

(6)

式中：km、kc、kq——常数；

IPM——转子永磁体激励的磁场等效至转矩绕组中的电流部分。

2 滑模观测器的设计

本文研究的对象是转矩绕组极对数pM=2、悬浮力绕组极对数pB=3的表贴式BPMSM。其转矩控制模块在静止两相坐标系α-β下的数学模型为

(7)

其中：A=(-RM/LM)·I

B=(1/LM)·I

式中：iM——转矩绕组α、β轴电流，iM=(iα，iβ)T；

uM——转矩绕组α、β轴电压，uM=(uα，uβ)T；

EM——转矩绕组α、β轴反电动势，EM=(Eα，Eβ)T；

RM——转矩绕组电阻；

LM——转矩绕组电感。

可定义滑模面S为

(8)

电流的滑模观测器为

(9)

且

h——滑模增益；

sgn——符号函数。

式(9)减去式(7)得转矩绕组电流观测误差的状态方程为

(10)

如果满足式(11)所示的滑模条件，则系统进入滑模状态：

(11)

滑模增益h必须足够大才能满足到达滑模状态的条件，但若其值过分大将会引起抖振噪声，从而导致估计误差，因此选择合适的滑模增益是问题的关键。取正定Lyapunov函数：

(12)

其中：

(13)

(14)

取滑模增益为

(15)

式中：δ——正常数。

A1，A2均小于0，从而使得U<0，满足滑模条件式(11)，进而系统得以进入滑模状态。此时，有

(16)

将式(16)代入式(10)，可得

EM=K

(17)

将不连续的含有高频成分的切换控制量经过适当的低通滤波器后得到等价控制量，即估算反电势：

(18)

(19)

根据式(12)、式(13)可计算求得转子位置角：

(20)

3 BPMSM无速度传感器控制系统仿真研究

浮力绕组极对数pB=3，永磁体励磁磁通ΨPM=0.175Wb，转矩绕组电阻RM=2.875Ω，转矩绕组电感LMd=LMq=LM=8.5mH，给定转速n*=8000r/min。

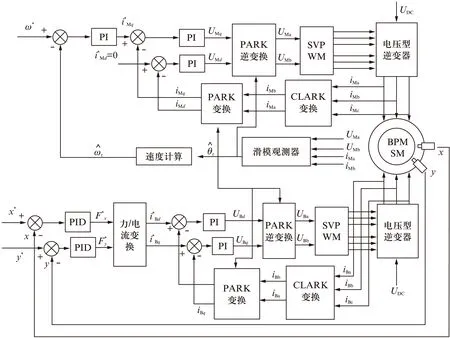
图1 基于滑模观测器的BPMSM无传感器矢量控制系统框图

图2 8000r/min转速下转子位置实测值与估计

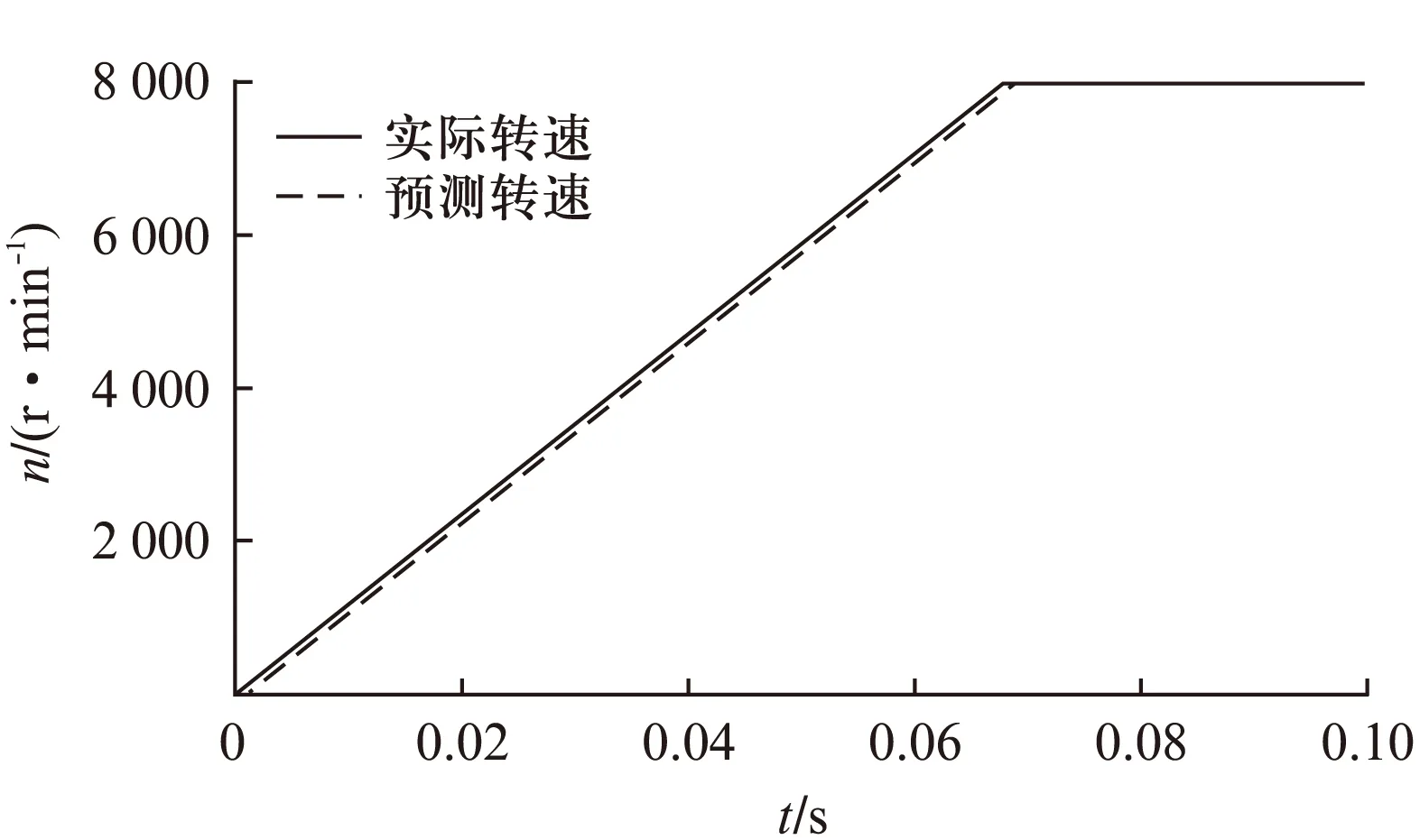
图3 转速实测值与估算值

图4 转子起伏波形图

4 结 语

本文采用滑模面及滑模等效控制方法，并基于转矩绕组观测电流和其实测电流差值构建滑模面，观测电机反电动势，从而实现转子位置角及转速的精确估算。利用MATLAB仿真软件构建了无速度传感器运行仿真系统，对电机转速、转角信号进行辨识。仿真结果表明： 滑模观测器的转角、转速信号辨识精度较高，并能满足BPMSM无速度传感方式的稳定悬浮运行要求，为今后搭建BPMSM无速度传感试验平台奠定了理论基础。

[1] THOMAS N, PHILIPP K, FRANZ Z, et al. Magnetically levitated slice motors-an overview[J]. IEEE Transactions on Industrial Applications， 2011, 47(2)： 754-766.

[2] 年珩，贺益康，黄雷.内插式永磁无轴承电机转子位置/位移综合自检测[J].中国电机工程学报，2007，27(9)： 53-58.

[3] 周令康，曹莉，王毅，等.基于高频注入法的无轴承同步磁阻电机无速度传感器研究[J].微电机，2012，45(10)： 43- 47.

[4] 朱熀秋，陈朝亮，邓建明，等.无轴承永磁同步电机无速度传感器控制系统[J].电机与控制应用，2008，35(5)： 18-22.

[5] 黄雷，崔迎.基于滑模观测器的永磁同步电机无传感器矢量控制[J].机电工程，2012，29(11)： 1303-1305.

[6] 陈坤华，孙玉坤，吴建兵，等.基于电感模型的开关磁阻电机无位置传感技术[J].电工技术学报，2006，21(11)： 71-75.

[7] BOSE B K. Modern power electronics and AC drives[M]. Beijing： Pearson Eduation North Asia Limited and China Mechine Press, 2002.

[8] CHEN Z Q, TOMITA M, ICHIKAWA S, et al. Sensorless control of interior permanent magnetic synchronous motor by estimation of an extended electromotive force[C]∥IEEE Industry Applocations Conferences, 2000： 1814-1819.

[9] 张猛. 无机械传感器永磁同步电机控制及磁链观测[D]. 北京： 清华大学, 2007.

[10] WANG L M, LORENZ R D. Rotor position estimation for permanent magnet synchronous motor using saliency-tracking self-sensing method[C]∥Proc of IEEE-IAS 2000 Annual Meeting, Rome, Italy, 2000： 445- 450.

[11] 李永东，朱昊.永磁同步电机无速度传感器控制综述[J].电气传动，2009,39(9)： 445- 450.

[12] LI H R, WANG J H, GU S S, et al. A Neural-network-based adaptive estimator of rotor position and speed for permanent magnet synchronous motor[C]∥IEEE ICEMS， 2001： 735-738.

Seneorless Vector Control of Bearingless Permanent Magnet Synchronous Motor Based on Sliding Mode Observer*

TAOTao，TANGMingjun,HUALianghao,ZHOUJie,LVZhixiang

(Department of Electronic and Electrical Engineering, Yangzhou Polytechnic Institute, Yangzhou 225127, China)

A novel control strategy based on sliding mode observer was present for the purpose of solving the problems of cost and reliability caused by the mechanical sensor of the bearingless permanent magnet synchronous motor (BPMSM) vector control system. The sliding-mode surface and the sliding-mode equivalent control method was used in the control system. And, the sliding-mode surface was defined on the errors between the actual and estimated currents. The estimated back-EMF was observed to calculate the angle and speed of the rotor. Simulation system of speed sensorless was constructed in MATLAB/Simulink environment and simulations of speed/angle identification for the rotor were carried out. The simulation results had showed that sliding mode observer speed/angle identification precision was very well and was able to achieve stable sensorless suspension running.

bearingless permanent magnet synchronous motor (BPMSM)； sliding mode observer； self-sensing for rotor speed； self-sensing for rotor angle

江苏省大学生实践创新训练计划(201513754005Y);扬州市重点研发项目(YZ2015084)

陶 涛(1988—)，男，硕士研究生，讲师，研究方向为无轴承电机智能控制技术。

TM 351

A

1673-6540(2016)10-0009-05

2016-06-18