基于SAS软件实现随机分组及应用

罗艳虹，胡良平

(1.山西医科大学公共卫生学院卫生统计学教研室，山西 太原 030001；2.世界中医药联合会临床科研统计学专业委员会，北京 100029；3.军事医学科学院生物医学统计学咨询中心，北京 100850*通信作者：胡良平，E-mail：lphu812@sina.com )



基于SAS软件实现随机分组及应用

罗艳虹1,2，胡良平2,3*

(1.山西医科大学公共卫生学院卫生统计学教研室，山西 太原 030001；2.世界中医药联合会临床科研统计学专业委员会，北京 100029；3.军事医学科学院生物医学统计学咨询中心，北京 100850*通信作者：胡良平，E-mail：lphu812@sina.com )

本文的目的是使读者能方便快捷地运用SAS软件中的PLAN过程实现随机分组。首先，对PLAN过程进行了简单介绍。接着，结合单因素设计、随机区组设计、具有重复试验的随机区组设计和拉丁方设计，介绍了随机分组的SAS实现方法。读者只需要修改本文中所呈现的SAS程序中的少量参数，就可很方便地用SAS软件实现自己的随机分组任务。事实说明，尽管SAS软件非常难学难用，但借助现成的SAS程序，可以轻松自如地解决很多具体问题。

SAS软件；随机分组；分层因素；单因素设计；随机区组设计；拉丁方设计

1 PLAN过程简介[1]

SAS/STAT模块中的PLAN过程，可用于生成各种设计方案(主要包括设计类型的架构、其内的受试对象的随机化分配)，同时可以对析因设计，尤其是嵌套设计、交叉设计和随机区组设计进行随机化(此处强调的是在各种设计类型下，如何实现受试对象的随机分组)。PLAN过程也可以生成一系列排列数和组合数，可生成以下多种试验设计类型并完成相应的受试对象的随机化操作。

析因设计，包括随机化和非随机化析因设计；平衡和部分平衡不完全区组设计；广义循环不完全区组设计；拉丁方设计。

对于其他类型的试验设计，尤其是分式析因设计、响应面和正交阵列设计，可以参考SAS/QC软件的FACTEX 和OPTEX过程及ADX(注：它是利用菜单驱动法实现试验设计的SAS模块)界面。

PROC PLAN生成设计方案的过程：首先选择第一个因素的各个水平；接着，对于第二个因素，PROC PLAN在第一个因素的每个水平下选择第二个因素的水平。总之，对于一个给定的因素，PLAN过程基于此因素之前的所有因素的水平组合来选择该因素的水平。

有五种不同的方法进行各因素水平的选择：随机选择，随机选择因素的各水平；顺序选择，每次以一个标准的顺序选择因素的各水平；循环选择，通过循环地排列先前的各水平生成当前各水平；排列选择，因素各水平是整数1～n的一个排列；组合选择，每次从整数1～n中选取m个数进行组合用以选择因素的m个水平。

随机选择方法可用于生成随机化设计方案。同时通过恰当使用循环选择，可以生成任何一种广义循环区组设计。因素的嵌套长度及随机设计方案的生成数目不受限制。可以同时选择若干因素，并设定最内层(也就是嵌套在最内层)因素。各因素的水平可以看作各个处理，应用于设计方案的各格子。出于该原因，列出的因素称为处理。运行PROC PLAN可以生成及随机化各种设计方案。

文献[2]详细地介绍了有关随机原则、概念和常用方法，下面将结合几种试验设计类型并运用SAS软件中的PLAN过程具体实现随机分组。

2 运用PLAN过程实现试验设计及其随机分组

2.1 单因素两水平设计及其随机分组

【例1】为试验“736”对肉瘤的抑制作用，将16只长出肉瘤的小鼠随机分为两组，试验组注射“736”，对照组注射同量生理盐水，10天后解剖称瘤重，观察两组瘤重之间的差异是否具有统计学意义[3-4]。请给出包含随机分组的具体设计方案。

【分析与解答】先将全部小鼠编成1～16号，并设所需要的SAS程序名为SASDESIGN1.SAS，程序语句如下：

odshtml; procplanseed=20150731; factorsxiaoshu=16; treatmentstreatment=16cyclic(1111111122222222); run; odshtmlclose;

【程序说明】第一句与最后一句分别是打开与关闭输出传输系统ODS，并采用网页格式输出结果，下同；“proc plan”调用SAS软件中的PLAN过程，选项“seed=20150731”的作用是设置产生随机数的初始种子数为20150731(通常为编写此程序的时间，种子数相同的程序，将永远产生出相同的随机结果，即随机结果具有重现性)；“factors xiaoshu=16”是该过程中一个重要语句，将生成代表受试对象“编号”的变量名“xiaoshu”及其取值(1～16)；“treatments treatment=16 cyclic (1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2)”中的“treatments”是该过程中一个语句，“treatment=16”代表“试验因素treatment有16个水平”，其实是假定16个受试对象中的每一个接受一种特定的“处理”，“cyclic (1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2)”进一步把前面的“16种处理”设置成“1”与“2”两种处理，即试验因素“treatments”实际为具有“1”与“2”两个水平的单因素，其中，“1”与“2”水平分别出现8次。

【主要输出结果及解释】

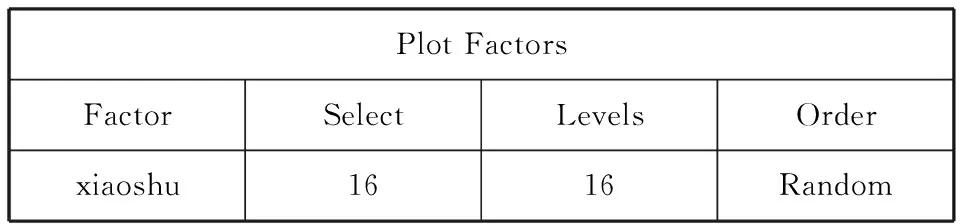
PlotFactorsFactorSelectLevelsOrderxiaoshu1616Random

TreatmentFactorsFactorSelectLevelsOrderInitialBlock/Incrementtreatment1616Cyclic(1111111122222222)/1

xiaoshutreatment161338127915614111241051111111122222222

16只小鼠的编号为1～16，从运行结果的第三部分可知：设计方案中编号(xiaoshu)为16、13、3、8、12、7、9、15的小鼠接受第一种处理；设计方案中编号(xiaoshu)为6、14、11、1、2、4、10、5的小鼠接受第二种处理。

【思考题】借助例1，如何修改上面的SAS程序，将32只小鼠随机均分为4组，即用SAS实现单因素4水平设计及其受试对象的随机分组。

2.2 随机区组设计及其随机分组

【例2】对未成年大白鼠注射3种不同剂量雌激素，一定时间后观测其子宫重量，做试验时，取4窝不同种系的大白鼠，每窝3只，随机分配到3个剂量组内进行试验[3-4]。请给出包含随机分组的具体设计方案。

【分析与解答】先将全部大白鼠按窝别编成1～4个区组，再将每个区组(即每窝)中的3只大白鼠编成1～3号，并设所需要的SAS程序名为SASDESIGN2.SAS，程序语句如下：

odshtml;procplanseed=20150731;factorsblock=4ordereddose=3;run;odshtmlclose;

【程序说明】在上述的过程中，有一个关键语句“factors”。该语句产生两个变量(即因素)，分别为“block”与“dose”，它们分别有4个水平与3个水平，它们的水平数乘积为12，意味着总共有12个受试对象；“ordered”声明要求将“block”的4个水平按其自然顺序排列，而“dose”后面没有“ordered”，表明要求将“dose”的3个水平(代表三种不同的剂量)随机化，而且，“dose”的3个水平必须在“block”的每一个水平条件下被随机化。

【主要分析结果及解释】

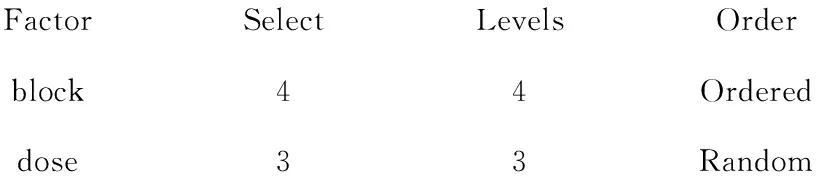
FactorSelectLevelsOrderblock44Ordereddose33Random

blockdose1312213231324321

上述结果表明，第1个区组中的3只大鼠注射的剂量大小分别为3、1、2；第2个区组中的3只大鼠注射的剂量大小分别为1、3、2；第3个区组中的3只大鼠注射的剂量大小分别为1、3、2；第4个区组中的3只大鼠注射的剂量大小分别为3、2、1。

【说明】本例的随机区组设计也可以理解成对12只大鼠进行“分层随机”分组，相当于将12只大鼠按“窝别”作为“分层因素”，先将它们按“窝别”形成4个“区组”，再在每个“区组”内采用完全随机方法，将每个区组内的3只大鼠随机分入3个试验组，这就是用“分层随机”实现单因素三水平设计的随机分组。

随机区组设计与用“分层随机”实现单因素三水平设计的区别在哪里？从用SAS软件实现随机化的做法来看，二者没有区别；从设计类型的名称和对定量资料统计分析角度看，二者之间是有区别的。区别在于：随机区组设计中包含两个因素，一个是试验因素(即研究者关心的因素)、另一个是重要非试验因素(即研究者原本不想关心，但它确实会对试验结果造成不可忽视的影响)，当需要对所收集的定量资料进行差异性分析时，首先应按两个因素来构建方差分析或秩和检验的“统计模型”，仅当“区组因素”对定量结果的影响无统计学意义时，可将其忽略，再采用单因素分析模型处理；而用“分层随机”实现单因素三水平设计的场合下，“区组因素”是出于“质量控制”的考虑，它是研究者基于基本常识和专业知识，从众多的非试验因素中找出来的唯一重要的非试验因素(注意：若有多个重要非试验因素，应将它们形成复合型的区组因素)，只是在对受试对象进行随机分组时发挥“区组因素”的“控制作用”，确保分入对比组中的受试对象在“区组因素”上是高度可比的。在对收集的定量资料进行差异性分析时，通常，可以直接将其视为来自“单因素多水平设计定量资料”，采取相应的统计模型进行处理。当然，若按“随机区组设计”的统计模型进行数据处理，则更为合适。

【思考题】借助例2，如何修改上面的SAS程序，将8窝(每窝4只)大白鼠随机均分入4个剂量组中去，即用SAS实现随机区组设计及其受试对象的随机分组。

2.3 具有重复试验的随机区组设计及其随机分组

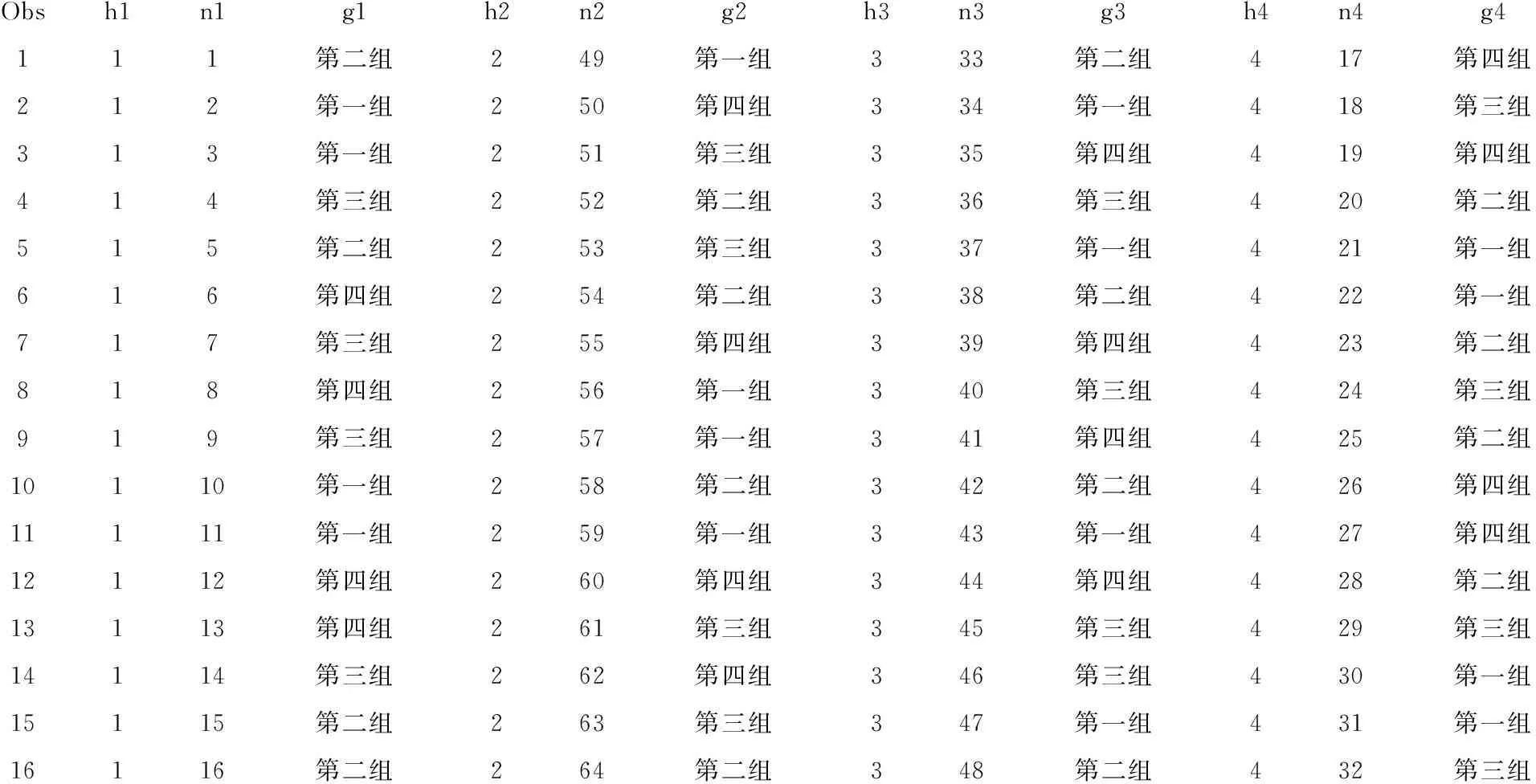
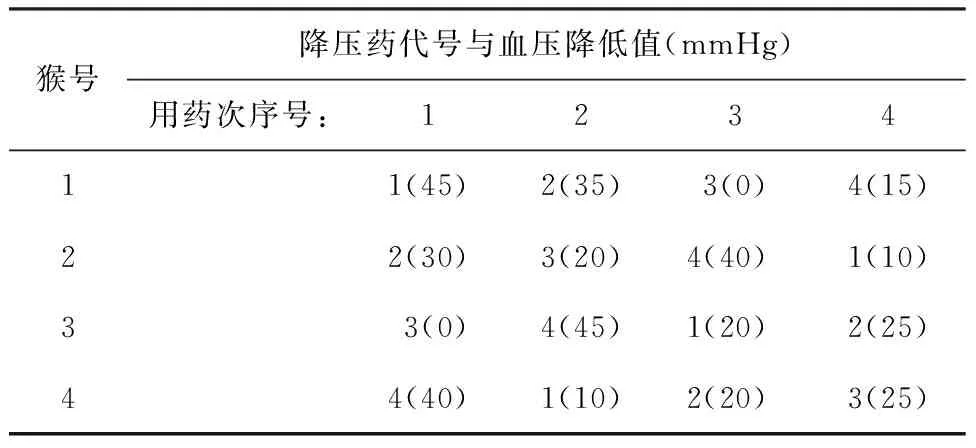
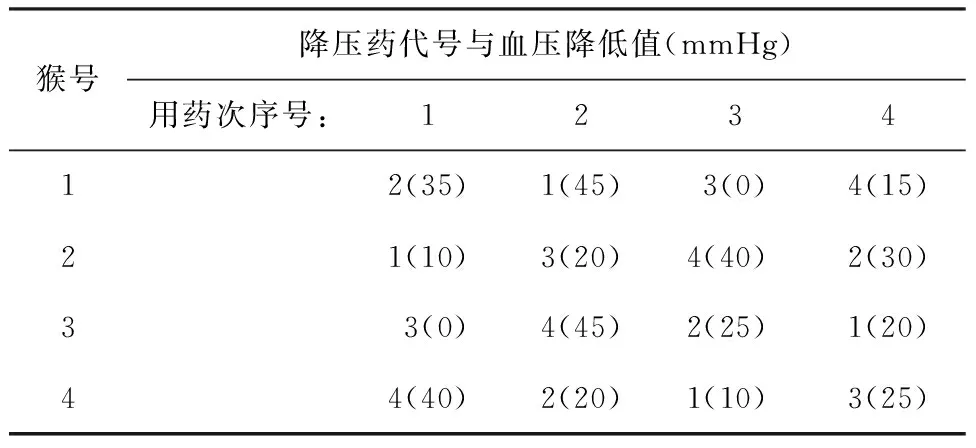
【例3】在4家医院开展某项临床试验，试以医院为分层因素，按照具有重复试验的随机区组设计将64例某病患者随机均分入4家医院，再将每家医院接收的16例受试者随机分入试验药物的4个不同剂量组，4组患者例数相等[5]。

【分析与解答】本例属于具有重复试验的随机区组设计，医院为“区组因素”、药物剂量为“试验因素”，每家医院的每个剂量组中均有4例受试者(即4次独立重复试验)。先将全部受试者编成1～64号，每相邻8位被视为“一个区组”，将每个区组中的8位受试者随机均分入4个剂量组。设所需要的SAS程序名为SASDESIGN3.SAS，程序语句如下：

%macro reptblock(seed=,hospital=,block=,length=,p_1=,p_2=,p_3=);

proc plan seed=&seed;

factors hospital=&hospital block=&block length=&length;

output out=a;run;

data b;set a;no=_n_;

if length<=&length*&p_1 then group=' 第一组';

else if &length*&p_1

else if &length*(&p_1+&p_2)

else group=' 第四组';run;

data c1(rename=(hospital=h1 no=n1 group=g1) drop=block length)

c2(rename=(hospital=h2 no=n2 group=g2) drop=block length)

c3(rename=(hospital=h3 no=n3 group=g3) drop=block length)

c4(rename=(hospital=h4 no=n4 group=g4) drop=block length);

set b;

if hospital=1 then output c1;

else if hospital=2 then output c2;

else if hospital=3 then output c3;

else output c4;

run;

data c;

merge c1 c2 c3 c4;

run;

proc print data=c;ods html;run;

%mend;

%reptblock(seed=20161004,hospital=4,block=2,length=8,p_1=1/4,p_2=1/4,p_3=1/4);

【程序说明】此程序比较复杂，因篇幅所限，详细说明可参阅文献[4]。

【主要分析结果及解释】

Obsh1n1g1h2n2g2h3n3g3h4n4g4111第二组249第一组333第二组417第四组212第一组250第四组334第一组418第三组313第一组251第三组335第四组419第四组414第三组252第二组336第三组420第二组515第二组253第三组337第一组421第一组616第四组254第二组338第二组422第一组717第三组255第四组339第四组423第二组818第四组256第一组340第三组424第三组919第三组257第一组341第四组425第二组10110第一组258第二组342第二组426第四组11111第一组259第一组343第一组427第四组12112第四组260第四组344第四组428第二组13113第四组261第三组345第三组429第三组14114第三组262第四组346第三组430第一组15115第二组263第三组347第一组431第一组16116第二组264第二组348第二组432第三组

上述结果表明：h1、n1、g1代表第1家医院的编号、受试者编号、剂量组编号；……；h4、n4、g4代表第4家医院的编号、受试者编号、剂量组编号。也就是说，1～16号受试者被分入第1家医院，17～32号受试者被分入第4家医院，33～48号受试者被分入第3家医院，49～64号受试者被分入第2家医院。分入每家医院的16例受试者再被随机分入4个剂量组，每个剂量组有4例受试者。

2.4 拉丁方设计及其随机分组

【例4】有4种降压药(设为A1，A2，A3，A4)对4只猴进行试验，每只猴用药4次，每次7天，间隔1个月，每次以用药前后舒张压下降值作为试验效应，已知因素之间交互作用可忽略不计，假定此药物的效应是短暂的且不会在本质上影响血压的取值[3-4]。请给出包含随机分组的具体设计方案。

【分析与解答】这是一个需要最少样本含量且可考察三个因素(一个试验因素、两个区组因素)的试验设计类型，但必须满足两个重要的前提条件：其一，三因素之间的交互作用可忽略不计；其二，试验因素对评价指标的影响是短暂的且不会在本质上对其有影响。例子中的试验因素为“降压药”，一般是不符合前述第二条假定的。采用拉丁方设计的试验因素最合适的类似如“体温计种类”或“天平种类”，次合适的类似如“血压计种类”，最不合适的类似如“药物种类”或“计量大小”。本例的主要目的是介绍在拉丁方设计中如何实现对受试对象的随机分组方法，而仅假定其试验因素“药物种类”符合此设计类型的要求。

先将4只猴(houzi)编成1-4号，将试验次序(cishu)编成1～4号，再将试验药物(yaowu)编成1～4号，并设所需要的SAS程序名为SASDESIGN4.SAS，程序语句如下：

odshtml;procplanseed=20150731;factorshouzi=4orderedcishu=4ordered;treatmentsyaowu=4cyclic;outputout=ayaowucvals=('yaowu1''yaowu2''yaowu3''yaowu4')ran-dom;run;procprintdata=a;run;odshtmlclose;

【程序说明】 第1个过程步调用PLAN过程构造拉丁方设计的架构(横行安排4只猴、纵列安排4个次序)(它们都按顺序排列，不是随机的)并将试验因素(yaowu)的4个水平进行循环排列，排成4行4列，即每行上都是1～4种药物的随机排列，共排出4行；“output out=a”是利用“output”语句，产生一个名为“a”的输出数据集，该数据集中存放着拉丁方设计的结果(包括架构和其内的随机排列)；位于“output out=a”之后的一行，目的是对试验因素“yaowu”的4个水平由原先的“循环排列”再行随机化排列。第2个过程步调用PRINT过程输出拉丁方设计的结果。

【主要分析结果及解释】

houzicishuyaowu112341234212342341312343412412344123

这个输出结果不太容易看懂，改成下面的形式就一目了然了，见表1。

表1 四种降压药用于4只猴的降压效果

注：假定表体内小括号内的数据为血压降低值

由表1可看出：猴号与用药次序号都是按顺序排列的，而表体内的降压药代号1～4是按循环规律排列的。以上属于常规拉丁方设计，但最好将表体内各行上的“降压药代号1～4”随机化排列，这就是下面的输出结果。

Obshouzicishuyaowu111yaowu2212yaowu1313yaowu3414yaowu4521yaowu1

622yaowu3723yaowu4824yaowu2931yaowu31032yaowu41133yaowu21234yaowu11341yaowu41442yaowu21543yaowu11644yaowu3

上面这个输出结果仍然不太容易看懂，改成下面的形式就一目了然了，见表2。

表2 四种降压药用于4只猴的降压效果

注：假定表体内小括号内的数据为血压降低值

表2的表体内4行上的“1～4”号的顺序与上面第二部分输出结果最后一列相对应，第1行：yaowu2、yaowu1、yaowu3、yaowu4；…；第4行：yaowu4、yaowu2、yaowu1、yaowu3。

[1] SAS Institute Inc.SAS/STAT 9.3 user’s Guide[M]. Cary, NC: SAS Institnte Inc, 2011: 3252-3347.

[2] 杨孟渊, 胡良平. 精神卫生科研如何严格遵守试验设计四原则之随机原则[J]. 四川精神卫生, 2016, 29(4): 289-294.

[3] 胡良平. 统计学三型理论在实验设计中的应用[M]. 北京: 人民军医出版社, 2006:44-106.

[4] 胡良平. 科研设计与统计分析[M]. 北京：军事医学科学出版社, 2012: 265-276.

[5] 胡良平. 课题设计与数据分析—关键技术与标准模板[M]. 北京: 军事医学科学出版社, 2014: 93-103.

(本文编辑：吴俊林)

Random grouping based on SAS software and its application

LUOYan-hong1,2,HULiang-ping2,3*

(1.DepartmentofHealthStatistics,AcaelemyofPublicHealth,ShanxiMedicalUniversity,Taiyuan030001,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China;3.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China*Correspondingauthor:HULiang-ping,E-mail:lphu812@sina.com)

The purpose of this paper is to enable readers to realize random grouping using PLAN procedure in SAS software quickly and easily. Firstly, the PLAN procedure was briefly introduced. Then, implementation of randomization by using SAS was introduced in this paper for a single factor design, a randomized block design, a randomized block design with repeated experiment and a Latin square design. Readers can easily use SAS software to achieve random grouping by modifying a few parameters of SAS programs presented in this paper. In fact, the readers can easily solve a lot of specific problems with the existing SAS programs, although SAS software is very difficult to learn and use.

SAS software; Random grouping; Stratification factor; Single factor design; Randomized block design; Latin square design

R195.1

A doi:10.11886/j.issn.1007-3256.2016.05.003

2016-10-11)