风电功率爬坡气象场景分类模型及阈值整定研究

熊　一　査晓明　秦　亮　欧阳庭辉　夏　添

(武汉大学电气工程学院　武汉　430072)



风电功率爬坡气象场景分类模型及阈值整定研究

熊一査晓明秦亮欧阳庭辉夏添

(武汉大学电气工程学院武汉430072)

为了判定和预报引发风电功率爬坡事件的风速突变的强对流气象类型，考虑风电场实际运行状态、电力系统运行方式以及区域电网的热备用启动速度和承受能力确定风电功率爬坡定义及其爬坡气象场景判定标准。在此定义上，引入支持向量标记法构造了风电功率爬坡场景分类的极小值和极大值的初始化模型，通过合适的显著性参数因子及预分类结果，建立风电功率爬坡场景分类模型。进而根据气象学物理意义分类出典型爬坡气象类型和相关特征因子阈值范围。实例分析表明，风电功率爬坡气象场景分类模型和确定的分类特征因子阈值对预报判别出目标区域风电功率爬坡气象类型有较好的指导作用。

风电功率爬坡爬坡场景定义支持向量标记分类模型优化分类阈值整定

0　引言

风电功率爬坡是指在较短时间内，风电功率上升或下降幅度较大，对区域电能质量产生较大影响且影响到电力调度计划的风电功率波动过程。随着风力发电的快速发展，风电并网装机容量的不断上升，受到自然气候不规律作用的风电功率波动对电力系统所产生的影响亟需有效的分析研究。

风电功率爬坡场景的产生原因(非人为因素)主要为季风性气候[1]、高压中心、强对流天气等气象原因。但由于长时间稳定的爬坡过程对电力系统的影响较小，所以不需要电力调度的特别干预。考虑到爬坡场景对电力系统影响较大的是日内(24 h内)短时大规模局地强对流天气，这里着重针对直接导致风电功率爬坡的气象物理场景进行筛选分类及爬坡气象场景阈值分析，以达到可以判断预报以强对流天气为主的爬坡气象类型。而强对流天气导致的国内外风电场非人为的典型风功率爬坡事件频发：AWS Truewind对美国西德克萨斯州2006年～2007年内超过50个重大风电功率爬坡事件进行了爬坡气象的分类分析[2]；2010年以来，甘肃酒泉和湖北随州的风电场群多次因强对流天气过境导致大面积风机脱网和保护性人为切机；澳大利亚塔斯马尼亚岛2006年内41个风功率爬坡事件直接说明重大爬坡事件的成因分析需要考虑爬坡气象的类型特征[3，4]。在不考虑人为因素和电气故障的情况下，导致风功率爬坡的根本原因是强对流爬坡天气，如何判别和分类爬坡气象是此处的关键问题。根据测量结果可得，不同类型的强对流爬坡气象之间的统计性差异很明显。由此，结合风电场实际运行状况、电力系统的调度方式以及区域电网的热备用启动速度和承受能力确定风电功率爬坡定义及强对流气象场景分类阈值，由此建立风电功率爬坡气象分类模型。

从目标区域的历史风电功率爬坡场景的气象数据筛选出与各类爬坡气象紧密相关的显著性特征，结合风电功率爬坡定义所对应的风速变化率，本文将采用支持向量机(Support Vector Machine，SVM)[5，6]延伸方法支持向量描述法(Support Vector Domain Description，SVDD)[7-9]构造风电功率爬坡气象场景分类的初始模型。在此基础上由模糊C-均值分类法(Fuzzy C-means，FCM)[10，11]，根据筛选出的显著性特征因子给出预分类结果，从而确定风功率爬坡气象场景分类模型及气象分类的边界阈值。根据整定的阈值判别和预报最具代表性的夏季和冬季的强对流气象场景，并对比同期的风电功率变化，进一步给出预报分析结果，以验证风电功率爬坡气象分类模型的准确性。

1　风电功率爬坡定义及其阈值分析

在不考虑人为风电机组调控和超过24 h、非剧烈气象波动条件下，从电网调度和热备用容量的角度出发，认为风电功率爬坡的定义是量化风电功率在区域电网最小反应时间内可以接受的最大功率变化阈值Pval， 以期达到：为爬坡场景预测指出需要关注的目标；为电力系统控制、调度、规划提供前期的数据分析；更好地认识风电功率变化规律。因此本文结合风电场实际运行状态、电力系统运行方式及区域电网的热备用启动速度和承受能力，确定风电功率P(t)时变爬坡定义式和爬坡定义阈值Pval为

(1)

根据热备用在高峰负荷时段风电场出力的安全约束式(2)和经济约束式(3)，得以确定Pval的阈值[12]。

(2)

式中，g(t)和h(t)为约束条件；α为显著性水平。

(3)

式中，G(t)为总收益；C(P(t))为发电成本；ρW和ρR分别为发电机和热备用电能电价；PR为热备用总容量。

在安全约束和经济约束下5类爬坡场景的风电功率随时间变化曲线如图1所示。同时参考德州电力可靠委员会(Electric Reliability Council of Texas，ERCOT)在实时调度运行中，机组或电厂的实际出力是否偏离接收到的基点指令是对电厂考核的重要项目。当机组出力超出考虑辅助服务调用的基点指令值时，将受到偏差处罚[12，13]。于是可以假设：对于一个风电穿透率约为20%的区域电网，热备用容量占比约为5%，Pval阈值设定为1 h内需启动80%的区域电网机组热备用容量，即风电功率每小时上下波动幅度占区域电网总容量的4%即为风电功率爬坡事件。

图1　风电功率在双约束下的变化Fig.1　Change of wind power on the dual constraints

以2012年甘肃省桥湾、黄麻滩风电场群采样间隔为5 min的总风电出力数据作为样本集。依据上述爬坡定义对该数据集进行历史爬坡场景筛选，是爬坡场景相关的强对流天气聚类分析的重要参考。因此提取出典型爬坡气象筛选的首要任务是识别出样本集中的历史爬坡场景，如图2所示。

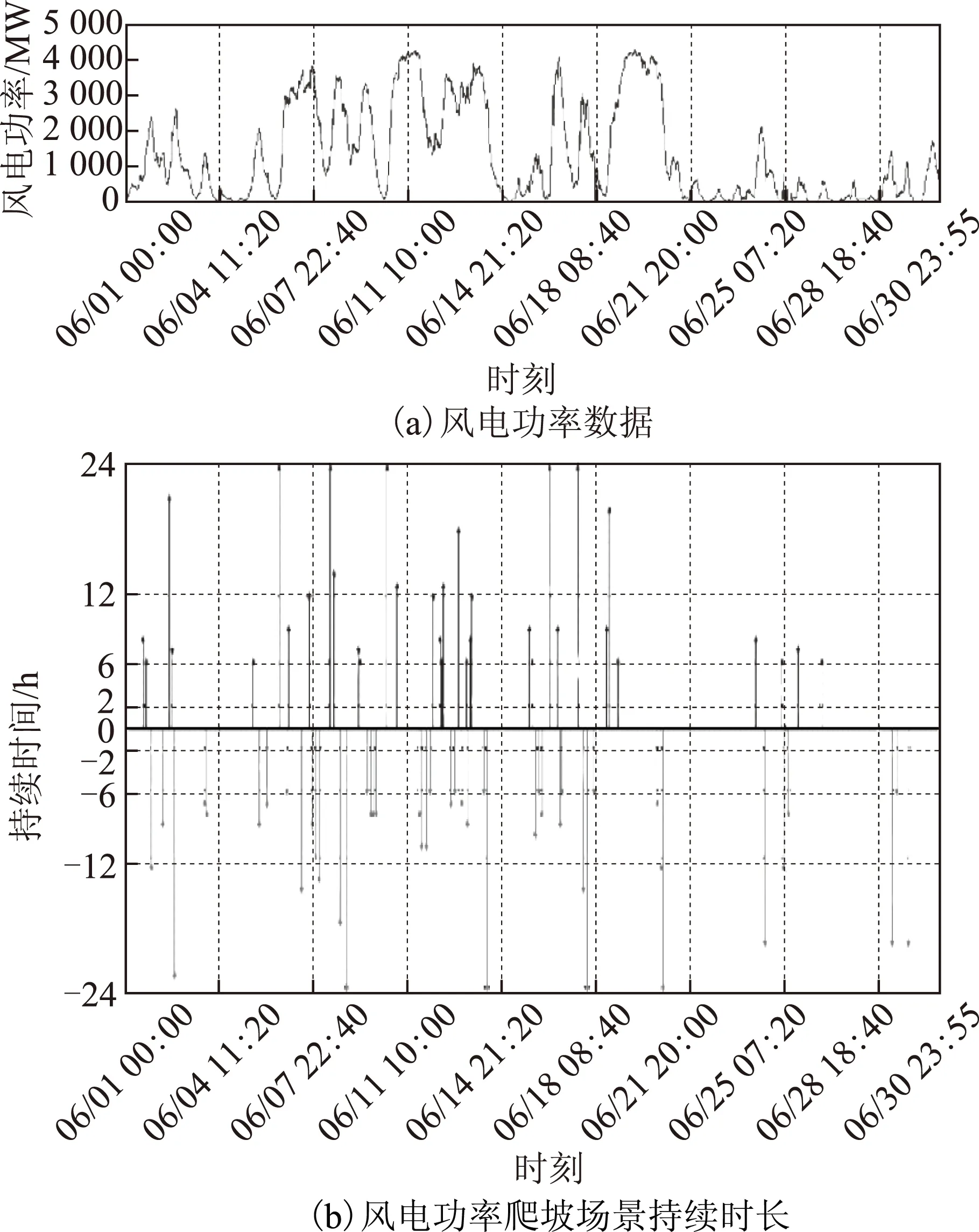
图2　爬坡定义下6月份目标风电场群风电功率及 对应爬坡场景持续时长Fig.2　Wind power and corresponding ramping events lasting time of wind farms in June by ramping definition

根据上述定义，对总装机容量为5 GW的风电场群，可以假设爬坡持续时间至少为2 h，且爬坡率大于200 MW/h的风电功率变化称为一个爬坡场景。对样

本集中的6月份的风电功率数据(图2a)进行爬坡识别，爬坡场景筛选结果如图2b所示。图2b中，横轴上方为正爬坡事件，横轴下方为负爬坡事件，纵坐标的绝对值代表对应爬坡场景的持续时间。由于风功率爬坡场景预报多采用1天前预报结果，将超过1天的持续爬坡过程的时长均处理为24 h。在筛选结果的基础上，可以提取对应气象学特征以进一步对引发爬坡场景的强对流天气聚类分析。

2　风电功率爬坡气象场景特征因子

采用甘肃省历史气象数据和风电功率数据，结合气象学中对大风区型的定义：50 km范围内、1.3 km高度以下、径向风速大于13 m/s(六级风)的区域，在第1节中风电功率爬坡场景定义的基础上选出了200个爬坡场景样本点。根据样本点的气象学参数和动力学、热力学指数所组成的预报因子：比湿、气压散度、涡度、相对湿度、温度露点差、水汽通量、假相对位温、垂直速度等13个参数因子及对流有效位能(Convective Available Potential Energy，CAPE)、沙氏指数(Showalter Index，SI)、风切变指数(Wind shear，Shr)、K指数(K Index，KI)、风暴强度指数(Storm Strength Index，SSI)、粗里查德逊数(Bulk Richardson Number，BRN)等10个指数因子[14,15]，其中选出与风电功率爬坡，尤其是风速变化相关的14个特征因子列入表1。

表1　预报因子分类及其相关系数Tab.1　Classification of predictors and correlation coefficient

在上述目标风电场群区域内选出的强对流天气的总样本数为200个。分别求出各样本的特征因子与以风速为指标的爬坡场景之间线性关系的皮尔森积矩相关系数r，即

(4)

式中，X、Y分别为预报因子和强对流天气风速指标的同期数据，具有数据连续性和线性相关性；n=200。当显著性水平α=0.05时，查表得相关系数r=0.194 6，计算结果见表1。

在考虑地域、气候背景和影响系统的前提下，使用逐步消空法[16-18]，根据置信剔除了大部分特征因子且剩余8个特征量：时间长度h、涡度ζ、 SI、CAPE、假相对位温θse、 气压梯度▽P、 Shr、TT。由于预报因子的分析计算和筛选是气象学在预报过程中的重要环节，将上述8个能够较好反映本文研究内容的预报因子作为预分类和SVDD的输入特征量。

3　风电功率爬坡气象场景分类初始模型

3.1风电功率爬坡气象场景分类极小值初始模型

支持向量聚类算法(SVDD)的主要研究思路是：在特征空间中寻找一个可以包围住所有训练集样本的最小超球体，并将该球体逆向映射回输入空间，由此可得到能描述数据分布区域边界的支持向量。

提出基于SVDD构造风电功率爬坡气象场景分类初始模型，对于爬坡气象场景的n个样本的数据集{x1,x2,…,xn}， xi∈Rd， 设超球体的中心α=(α1,α2,…,αd)， 则风电功率爬坡气象场景的目标函数为

s.t.‖Φ(xi)-α‖2≤R2+ξi

ξi≥0i=1,…,N

(5)

式中，‖·‖为欧氏距离；ξ=(ξ1,ξ2,…,ξN)T为松弛变量，允许训练样本在一定数量上出现在半径为R的超球体外部，引入c作为惩罚因子来平衡半径和松弛变量的比重，同时也可以控制外点规模和抑制噪声数据点。通常c的取值范围是[0，1]。引入Lagrange乘子β=(β1，…,βN)T， 由此可得风电功率爬坡气象场景分类极小值初始模型为

(6)

式中，K(,)为核函数，特选用高斯径向基核K(xi,xj)=exp(-q‖xi-xj‖2)，q为核函数宽度。当x1=x2时，K(xi,xj)=1， 代入式(6)可得出简化风电功率爬坡气象场景分类极小值初始模型为

(7)

同时，训练集中样本x距离超球体中心α的距离可表示为

R2(x)=‖Φ(x)-α‖2

(8)

式中，βi>0， 由此组成了支持函数，函数决定了半径R和样本与超球体中心的距离。

3.2风电功率爬坡气象场景分类极大值初始模型

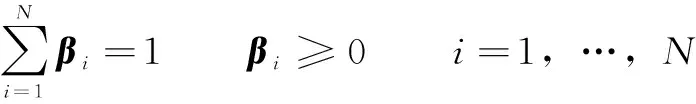
(9)

式中，p为非负数，由此可得βi的第k(k>1)轮迭代规则为

(10)

由此求解风电功率爬坡气象场景分类初始模型的迭代步骤明显降低。因训练集中的大部分爬坡气象场景数据对最终建立支持函数的作用较小，故构建分类模型之前需将其清除。这是基于支持向量描述法构造风电功率爬坡气象场景分类初始模型相对于其他传统聚类算法的核心优势之一。

4　初始模型参数选择及模型确定

4.1分类模型输入量求解

由于风电功率爬坡气象场景分类模型与特征因子阈值计算需要预分类的粗聚类结果作为输入量，所以需要引入以欧式距离为核心的聚类方法。

风电场气象场景数据均为确定性样本，根据各类聚类算法特点[19，20]，本文在风电场气象场景预分类选用模糊C-均值聚类。该方法是将风电场气象场景数据的N个样本的数据集X={x1k,x2k,…,xNk}， 其中每个对象xk有n个特性指标，如果把X分成C类，则它的每个分类结果对应一个C×N阶的Boolean矩阵U=[uik]C×N， 对应的模糊C-均值划分空间为[21-23]

在此空间上，模糊C-均值算法为

1≤i≤Cl=1,2,…

(11)

并计算距离

1≤i≤C1≤k≤n

(12)

将某省风电场群2012年的200个强对流天气场景的数据引入式(11)和式(12)可得风电场气象场景数据的预分类结果，如图3所示。图中的点元素对应一个Boolean矩阵的元素uik。为了清晰表达预分类结果，选取横坐标为有效位能指数CAPE，纵坐标为假相对位温θse， 且均为标幺值。

图3　200个数据样本Fig.3　200 samples

从图3可以看出在本文样本空间的预分类结果为模糊状4类。并将模糊状分类结果导入风电功率爬坡气象场景分类初始模型作为输入数据。

4.2已知样本训练及初始模型参数选择

选取某省2012年区域风电场群气象场景中确定引发风电功率爬坡的50个已知气象学物理意义的强对流天气样本数据进行训练，从而优化风电功率爬坡气象场景分类模型参数q和c，其参数变化所对应的聚类结果如图4所示。图4中的样本点满足超过13 m/s风速的持续时间大于2 h，且大风期间前后有大于3 m/s的持续性风速落差。

图4　不同q参数下的分类模型输出Fig.4　Classification model output of different q

图4中，聚类范围由“•”组成的边界特征点依次连接表示。当c为0.44，q值从0.5到5，由于高斯径向基核函数是一个关于q的单调减函数，故聚类结果呈单调递减的过程。由图4d可以看出，当q=4，c=0.44时，聚类与预分类结果一致且聚类准确清晰。不难发现，只有选取了合适的风电功率爬坡气象场景分类初始模型参数，最终才能得到风电功率爬坡气象场景分类模型。

5　爬坡场景分类的特征因子阈值整定

根据分类模型参数优化值(q=4，c=0.44)，可知4.2节中爬坡场景的样本点被分为4类，进一步引入已知样本的对应气象物理意义，即每一类分别对应一个主要爬坡气象。每类爬坡气象由8个气象特征因子来判定，其中本节以各类爬坡气象边界样本的特征因子的极值(阈值)为爬坡气象分类结果主要研究对象。

判定一个样本是否为风电功率爬坡气象场景分类模型边界样本，需要检查其k个邻近样本中，是否大

多数样本都位于该样本的切线一侧。由此，设当前样本xi(i∈[1,N])的k个邻近样本xj(j=1,…,N)， 使用BEPS算法计算各类风电功率爬坡气象场景的边界极值的步骤如下：

1)初始化阈值γ(0<γ<1)， γ用于控制簇边界的曲率，通常小于0.1。

4)气象场景数据边界样本识别。如果li≥1-γ， 则有xi为气象场景数据的边界数据。

由此可以计算出簇边界样本，进而得到分类边界值，即分类模型的特征因子阈值。即通过在第2节中使用的时间长度、涡度、SI、CAPE、假相对位温、气压梯度、SHR、TT这8个特征量可以得到4个分类及每类8个特征因子阈值。

引发爬坡场景的4类强对流天气的特点主要由发生时长(一般冷锋过境和干线比风切变持续时间长)以及作用于电力系统运行调度中的影响强度(一般雷暴大风和风切变影响程度较大)来细化区分。而持续时间较长(超过24 h)且变化缓慢的爬坡场景的气象过程可由区域电网AGC及时响应后平抑化处理，故不在此重点讨论。

虽然爬坡气象类型并不止4类，但本文样本空间做对应的气象聚类分析结果显示为最具代表性的典型风电功率爬坡气象场景见表2。

表2　典型风电功率爬坡气象场景特征量阈值范围Tab.2　Threshold range of characteristic quantity in typical wind power ramp scenario

由表2可得，凡是引入目标风电场群风电功率变化所对应的气象样本点均可由其8个特征因子的阈值范围确定对应的上述4类典型爬坡气象类型。

6　模型实验验证与分类特征因子阈值应用

为了进一步说明爬坡气象分类的必要性和2012年数据算得的分类模型及阈值的准确性，特选取目标风电场群(5 GW)所在区域强对流天气频繁出现的2013年5月中旬夏季数据进行分析，并将分类得出的爬坡气象与风功率爬坡场景相对应。

引用第4节选取的优化值(q=4，c=0.44)和特征因子阈值得到本文分类模型计算的风电功率爬坡气象场景分析结果与实际情况的对应关系如图5所示。

图5　典型爬坡气象分析Fig.5　Typical ramping weather analysis

从图5中可以看出，因风切变、冷锋过境和低压强对流使得风功率有几波陡升的过程；但由于陡升过程爬坡速度较快，风速超过了风机额定切机风速，导致局部或大面积风机脱网，从而引发风功率陡降；且图中的风功率正向爬坡过后因气象条件的消散也伴随着对应的负向爬坡过程。

由于气象特征随季节变化，尤其是春夏区别较大，为了说明上述4类爬坡气象类型符合全年变化需求，特选取2013年12月目标区域部分风电场群(0.2 GW)的冬季气象变化及其风功率变化对应分析如图6所示。

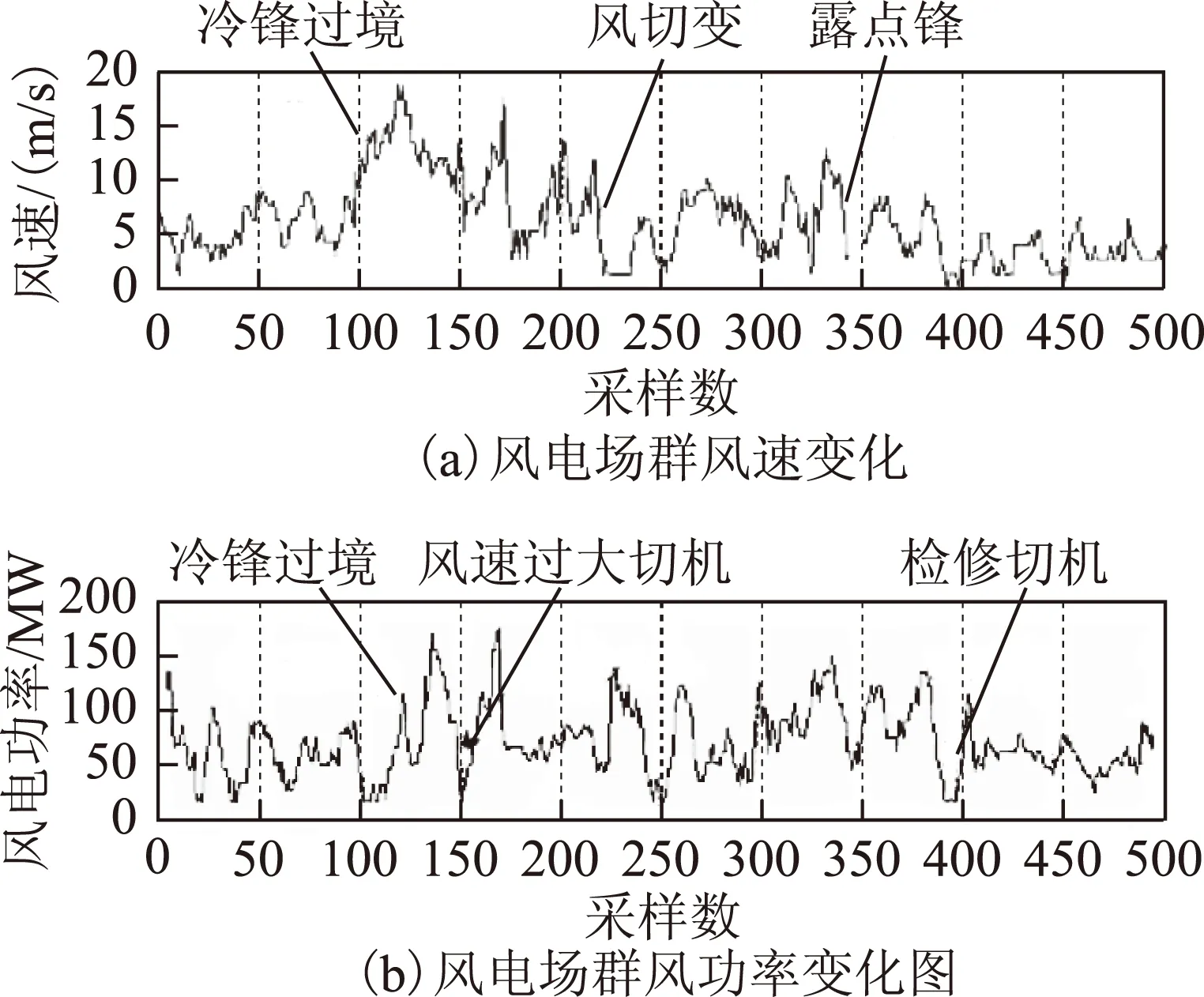
图6　目标风电场群风速变化及风功率变化Fig.6　Wind speed and wind power variation of wind farms

从图6中可以看出，仍然可以准确预报出上述4类爬坡天气，并与同期风功率变化相对应。由于篇幅所限，此处所考虑的引发风电功率爬坡气象场景集中在第5节中的4类典型的强对流天气[24-26]。根据2012年整定的风电功率爬坡气象场景的分类阈值，对2013年目标风电场群所在区域的60个气象场景进行判定分析见表3。

表3　爬坡气象场景分析Tab.3　Analysis of ramping climate scenario

由表3可知，根据爬坡场景特征因子阈值判定的结果显示正确判定的样本数比例达到83.3%。所以本文构造的风电功率爬坡气象场景分类模型及其特征因子阈值范围可以涵盖在目标区域风电场的风电功率爬坡气象及风速预报，且适用于夏季(5月)和冬季(12月)风电功率爬坡气象场景，说明该分类模型对爬坡气象判别有良好的适用性。

7　结论

1)在电力系统安全稳定运行和经济性调度的基础上，给出了风功率爬坡场景的定义及爬坡阈值分析。

2)基于支持向量描述法构造风电功率爬坡气象场景分类初始模型，并对初始模型参数进行优化选取，得到风电功率爬坡气象场景分类模型。并且根据目标风电场群区域2012年数据给出了4类爬坡气象及每类8个气象特征因子阈值。

3)选取某省风电场群2013年不同季节气象数据验证本文导出的风电功率爬坡气象场景分类模型和分类特征因子边界阈值，实验结果表明，导出的基于NWP数据中的分类模型和分类特征因子阈值对影响风电功率变化的强对流天气的判别有较好的指导作用。

[1]杨正瓴，冯勇，熊定方，等.基于季风特性改进风电功率预测的研究展望[J].智能电网，2015，3(1)：1-7.

Yang Zhengling，Feng Yong，Xiong Dingfang，et al.Research prospects of improvement in wind power forecasting based on characteristics of monsoons[J].Smart Grid，2015，3(1)：1-7.

[2]Freedman J，Markus M，Penc R.Analysis of west texas wind plant ramp-up and ramp-down events[R].AWS Truewind LLC，Albany，N.Y.，2008

[3]Ghelli A，Primo C.On the use of the extreme dependency score to investigate the performance of an NWP model for rare events[J].Meteorological Applications，2009，16(4)：537-544.

[4]Cutler N，Kay M，Outhred H，et al.High-risk scenarios for wind power forecasting in australia[C]//Proceedings of the European Wind Energy Conference & Exhibition (EWEC)，Milan，Italy，2007.

[5]Vladimir N.Vapnik.统计学习理论的本质[M].张学工，译.北京：清华大学出版社，2000.

[6]Cortes C，Vapnik V.Support-vector networks[J].Machine Learning，1995，20(3)：274-288.

[7]Burges C J C.A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery，1998，2(2)：123-132.

[8]Tax D M J，Duin R P W.Support vector domain description[J].Pattern Recognition Letters，1999，20(11-13)：1191-1199.

[9]Tax D M J，Duin R P W.Support vector domain description[J].Machine Learning，2004，54(1)：45-66.

[10]高新波.模糊聚类分析及其应用[M].西安：西安电子科技大学出版社，2004.

[11]何清.模糊聚类分析理论与应用研究进展[J].模糊系统与数学，1998(2)：12-17.

He Qing.Fuzzy cluster analysis theory and application research progress[J].Fuzzy Systems and Mathematics，1998 (2)：12-17.

[12]熊一，査晓明，秦亮，等.基于强对流天气判别的风功率爬坡预报方法研究[J].中国电机工程学报，2016，36(10)：2690-2698.

Xiong Yi, Zha Xiaoming,Qin Liang，et al.Research on wind power ramping prediction based on the strong convective weather discriminant method[J].Proceedings of the CSEE,2016,36(10):2690-2698.

[13]罗旭，马珂.美国得克萨斯州电力可靠性委员会在风电调度运行管理方面的经验和启示[J].电网技术，2011，35(10)：21-30.

Luo Xu，Ma Ke.Experience and enlightenment in operations of wind generation in ERCOT grid[J].Power System Technology，2011，35(10)：21-30.

[14]赵秀英，吴宝俊.风暴强度指数SSI[J].气象，2000，26(5)：55-56.

Zhao Xiuying，Wu Baojun.Storm severity index(SSI) [J].Meteorological Monthly，2000，26(5)：55-56.

[15]高守亭，孙淑清.应用里查逊数判别中尺度波动的不稳定[J].大气科学，1986，10(2)：171-182.

Gao Shouting，Sun Shuqing.Determining the instability of mesoscale perturbation swith richardson number[J].Scientia Atmospherica Sinica，1986，10(2)：171-182.

[16]Johns R H，Doswell C A I.Severe local storms forecasting[J].Weather and Forecasting，1992，7(4)：588-612.

[17]Halverson J B，Rickenbach T，Roy B，et al.Environmental characteristics of convective systems during TRMM-LBA[J].Monthly Weather Review，2002，130 (6)：12-18.

[18]刘玉玲.对流参数在强对流天气潜势预测中的作用[J].气象科技，2003，31(3)：24-29.

Liu Yuling.The role of convective parameters in strong convective weather potential prediction[J].Journal of Meteorological Science and Technology，2003，31(3)：24-29.

[19]Bezdek J C，Keller J，Krishnapuram R，et al.Fuzzy models and algorithms for pattern recognition and image processing[M]//Dubois D，Prade H.The Handbooks of Fuzzy Sets Series.New York：Springer，1999：146-157.

[20]Krishnapuram R，Keller J M.A possibilistic approach to clustering[J].IEEE Transactions on Fuzzy Systems，1993(1)：98-110.

[21]Pal N R，Pal K，Bezdek J C.A mixed c-means clustering model[C]//Proceedings of the 6th IEEE International Conference on Fuzzy Systems，Barcelona，1997(1)：11-21.

[22]Wu K L，Yang M S.Alternative c-means clustering algorithms[J].Pattern Recognition，2002，35(10)：64-68.

[23]Le K.Fuzzy relation compositions and pattern recognition[J].Journal of Information Science，1996，89(1)：74-87.

[24]戚永志，刘玉田.风光储联合系统输出功率滚动优化与实时控制[J]电工技术学报，2014，29(8)：265-273.

Qi Yongzhi，Liu Yutian.Output power rolling optimization and real-time control in wind-photovoltaic-storage hybrid system[J].Transactions of China Electrotechnical Society，2014，29(8)：265-273.

[25]刘方，杨秀，时珊珊，等.基于序列运算的微网经济优化调度[J]电工技术学报，2015，30(10)：227-237.

Liu Fang，Yang Xiu，Shi Shanshan，et al.Economic operation of micro-grid based on sequence operation[J].Transactions of China Electrotechnical Society，2015，30(10)：227-237.

[26]修春波，任晓，李艳晴，等.基于卡尔曼滤波的风速序列短期预测方法[J]电工技术学报，2014，29(2)：253-259.

Xiu Chunbo，Ren Xiao，Li Yanqing，et al.Short-term prediction method of wind speed series based on Kalman filtering fusion[J].Transactions of China Electrotechnical Society，2014，29(2)：253-259.

Study on Wind Power Ramping Weather Scenario Classification Model and Threshold Setting

Xiong YiZha XiaomingQin LiangOuyang TinghuiXia Tian

(School of Electrical EngineeringWuhan UniversityWuhan430072China)

Judging and forecasting types of strong convective weather causing velocity mutation are important to wind power ramping events.By considering the actual wind farm operation of regional power grid，power system operation mode，and the starting speed and capacity of hot standby，the definition of the wind power ramping and decision criteria of ramping weather scenario are determined.Based on this definition，the introduction of the support vector domain description method for wind power ramping scenario classification is used to establish an initializaed extremum model.Through appropriate significant parameters and preliminary classification results，the wind power ramping scenario classification model is established.Then according to the meteorological meaning，typical ramping weather types and related characteristics parameter thresholds are obtained.As a result，the case study shows that the establishment of the wind power ramping scenario classification model and the settled classification thresholds of the significant parameters can provide a good guidance for judging and forecasting the wind power ramping weather types in the target area.

Ramping of wind power，definition of ramping scenario，supported vector domain description，optimization of classification model，classification threshold setting

国家重点基础研究发展(973)计划 (2012CB215101)和国家自然科学基金(51177113)资助项目。

2016-03-15改稿日期2016-07-07

TM73

熊一男，1988年生，博士研究生，研究方向为电能质量、风功率预测、微电网与新能源并网等。

E-mail：xiongyi2010@qq.com(通信作者)

査晓明男，1967年生，教授，博士生导师，研究方向为电力电子功率变换及系统、智能电网及新能源发电中的电力电子技术应用等。

E-mail：xmzha@whu.edu.cn