整体把握教材，注重有效衔接

陈莉红　王淼生

一、小学、初中及高中知识衔接的教学现状

我国中小学数学教育要求教师在实施教学时要整体把握教材，注重各学段知识的有效衔接。遗憾的是，在实际教学中出现以下现象：各个学段的教师要么抱着“各人自扫门前雪，莫管他人瓦上霜”的态度只管自己这一段，导致小学、初中及高中的教学内容严重脱节出现盲区，不利于知识系统性，破坏知识的连贯性；要么抱着“以越位求到位”的心态随意提前教授高学段知识，超越学生已有认知水平与心理承受能力，挫伤学生学习数学积极性，不利于优化学生数学思维品质。

二、 确定学段边界，顺应思维发展，自然对接

以凸多边形内角和为例：

求任意凸多边形内角和，不仅对小学生，甚至对于初中生来说也较为困难。怎么办？我们可以先探究最简单的凸多边形，即三角形，正如著名数学家华罗庚所说：“要善于退，足够地退，退到最原始而不失去重要性的地方，是学好数学的诀窍。” 那如何求三角形内角和呢？让我们顺着教科书主编意图一起来回顾吧。

1.三角形内角和

1.1小学测量拼接验证法

方法1：借助量角器直接测量三个内角的度数，然后相加得到三角形三个内角的和等于180°（这种方法的优点是简单直接，易于操作，便于理解接受，不足之处在于测量有误差，学生通过测量得出的结果可能不是180°，易引发学生对结论产生怀疑，教师要适时引导，合理解释，并用拼接的方法进一步验证）。

方法2：用一张三角形纸片，把三角形的三个内角剪下来，然后拼在一起，通过观察发现正好是一个平角，于是得到三角形内角和等于180°。

上述方法1与方法2正是小学生得到三角形内角和等于180°的思维方法与实施过程，符合小学生认知特点，其本质就是通过实验与操作，初步验证三角形内角和定理，建立初步的直觉意识，培养学生动手操作，观察猜想的能力。那么老师可以设问这种验证的方法能说明任何一个三角形内角和都是180°吗？要解决这个问题就必须对数学结论给予严格证明，这为初中继续探究与论证指明了方向，埋下了伏笔，这就是小学阶段这一知识的边界。

1.2初中几何论证法

方法3：过三角形任意一顶点作对边的平行线，有三种作法如图1、图2、图3所示，利用平行线性质定理即可证得三角形内角和为180°。

方法4：在三角形某条边上任取一点（不含端点）分别作另两边的平行线（如边AC上任取一点D，过D作DE∥AB，DF∥BC，分别相交于E、F，如图4所示），利用平行线性质即可证得三角形内角和为180°。

方法5：在三角形内任取一点（不含边界），过D分别作AB、BC、CA平行线，分别相交于E、F；G、H；M、N，如图5所示，利用平行线基本性质即可证得三角形内角和为180°。

上述方法3、方法4、方法5分别借助三角形顶点，边上的点，内部的点构造平角的模型，从而实现三角形三个内角向共点平角的转化。方法4和方法5是方法3的延伸和拓展，而方法3又是怎么想到的呢？其本质就是上述小学方法2从“实物”转化为数学模型的过程，是具体到抽象的历程，是一次质的飞跃。这个问题在教学过程中的处理尤为重要，教师应充分利用小学阶段的拼接图形为直观模型，进行观察抽象，引导学生动手画出几何图形，并作出辅助线，由此即完成了从小学直观验证到初中几何论证的自然对接，顺应了学生的思维发展。

2.凸多边形内角和

从运动与静止的相对关系来看，对于三角形可以让一个人沿着三角形周围走一圈，会发现这个人也正好转了一圈回到原处，即三角形外角和等于360度；让人沿着凸n边形周围走一圈，最后还是回到原处，这就说明凸n边形外角和是一个定值，恒为360°。

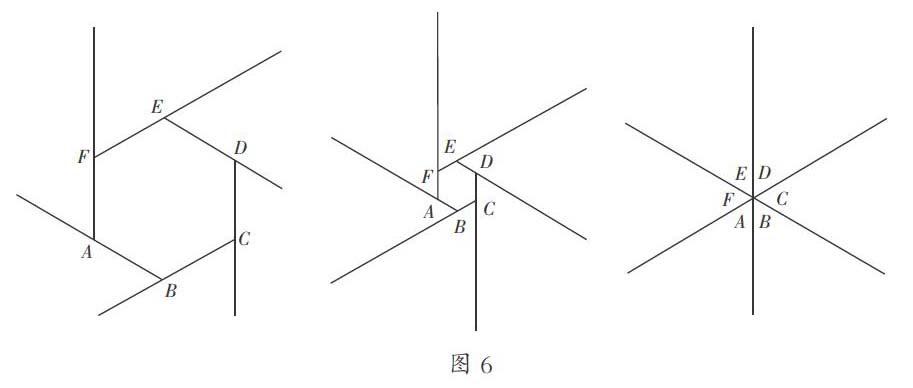
事实上，我们还可以由以下方法得到凸n边形外角和恒为360°，如图6所示。

有了这一新的发现，我们可以得到以下方法：

证法1：对于凸n边形，我们将凸n边形每一条边都向同一个时针方向延长（射线），如图6中的第一个图，此时发现有n个平角，但是要减去所有的外角，故n边形内角和：

n×180°-360°=（n-2）x180°。

对于上述得到的凸n边形内角和等于（n-2）x180°，还可以有其他方法吗？我们观察（n-2）x180°相当于n-2个三角形内角和，为此得到：

证法2：对于凸n（n≥3，n∈N）边形A1A2A3……An，任取其中一个顶点，不妨取A1，将A1分别与A3、A4、…、An-1连接，这样的连线将凸n边形分割成n-2个三角形，如图7所示，故凸n边形内角和为（n-2）x180°。

由证法2可知，凸多边形内角和可以转化为三角形内角和进行求解，三角形是初中阶段的基本图形，任意凸多边形都可以分割转化为多个三角形，这是一种基本的解题思路，也是在教学过程中必须让学生掌握的方法。由特殊到一般，我们还可以在多边形内部任取一点O（如图8所示），或在多边形的边上任取一点O（不含端点）（如图9所示），甚至在多边形外部任取一点，即平面内任取一点与多边形顶点连接，对多边形进行分割，都可以证得结论成立（证明过程略）。

由以上方法可知，几何证明教学中，教会学生画图、识图，多角度探究与思考，掌握基本图形的性质，渗透模型思想，从特殊到一般，转化和化归的思想等培养学生的几何直观，是初中阶段的边界。

上述都是从分割的角度来思考，能否从有限与无限的辩证关系来寻求问题的解决呢？

3.高中数学归纳法

证法3：（类比、归纳与猜想）三角形内角和等于180°，四边形内角和呢？五边形呢？凸n边形呢？同样采取分割的方法可知：

当n=4时，2×180°=（4-2）×180°=360°。

当n=5时，3×180°=（5-2）×180°=540°。