股指期货最优套期保值策略研究——基于投资者风险偏好差异视角

○郭建华

(邵阳学院 经济与管理系， 湖南 邵阳 422000)



股指期货最优套期保值策略研究
——基于投资者风险偏好差异视角

○郭建华

(邵阳学院 经济与管理系， 湖南 邵阳 422000)

利用股指期货进行套期保值操作可以为投资者进行市场风险规避。然而不同投资者对风险的偏好程度并不一致，他们采取的套期保值策略也会有所差异。文章通过把均值方差效用函数与风险厌恶系数相结合，构建不同风险偏好投资者的风险规避目标函数，然后借助小波分析方法，计算动态最优套期保值比，最后分析了最优套期保值比、套期保值效果与投资者风险偏好程度、套期保值期限的关系。结果表明，风险偏好型投资者通常采用低套期保值比，套期保值效果也略差；期限越长，最优套期保值比也越高。

风险偏好； 股指期货； 套期保值策略； 小波分析

一、引言

投资者买卖股票通常面临两种风险：系统风险和非系统风险，非系统风险可以通过组合投资的方式来消除或降低，然而不管是发达国家还是新兴金融市场，系统性风险均占总风险的很大比重，尤其是面对发育尚不成熟的中国股市，系统性风险所占比例超过非系统性风险[1]，投资组合却无能为力。利用股指期货进行套期保值操作，是一种很好的风险管理方法。因此，在我国成功推出股指期货这一良好工具的同时，如何合理利用好股指期货的套期保值功能，是投资者乃至整个金融界面临的一个重大课题。

利用股指期货进行套期保值操作的核心问题包括确定合理的套期保值目标函数和估计最优套期保值比[2][3]。Keynes[4]和Hicks[5]认为，所有金融衍生品市场参与者都出于风险厌恶的本性，希望通过套期保值来完全消除与某一特定商品有关的价格风险，因而最优的风险对冲策略就是保持套期比恒为1。显然，这种“完全”的套期保值策略由于忽视了基差风险的存在，因而不具有实际意义。后来，Johnson[6]根据马科维茨的资产组合理论，提出套期保值组合收益方差最小化的套期保值思想，自此开启了现代套期保值理论的先河。Ederington[7]根据Johnson的思想并借助最小二乘法，提出基于最小二乘法的套期保值模型，该模型形式直观且操作方便，所以在相当长一段时间内被认为是套期保值的主流模型。然而随着计量经济学的发展，学者们认为最小二乘套期保值模型没有考虑现货与期货价格序列间的协整关系，会造成估计上的偏误。尤其是20世纪90年代以来，随着对GARCH模型和Copula技术研究的深入，为研究金融时间序列的时变方差效应和波动聚集特征奠定了方法论基础，基于GARCH模型的套期保值比率估计方法不断出现。如Hsu等(2008)[8]将标普500指数和金融时报100指数作为研究样本构建了套保比率的Copula-GARCH模型。马超群等(2011)[9]基于Copula-GARCH模型对外汇期货的最优套期保值比率进行了研究。谢赤等(2013)[10]通过构建M-Copula-GJR-VaR动态套期保值比率估计模型，并采用中国市场现货价格和期货价格数据，对比分析了M-Copula-GJR-VaR模型与CCC-GARCH-VaR模型、DCC-GARCH-VaR等模型的套期保值比率和套期保值效果。代军等(2014)[11]通过在VECM-GARCH模型中引入非对称基差，研究了基差对我国沪深300股指期货和现货回报的条件均值与风险结构影响的非对称效应。彭红枫和陈奕(2015)[12]将区制转移应用到套期保值模型构建中，将MRS模型与GARCH模型相结合，建立了MRS-DCC模型，并用于估算铜期货市场的套期保值比率。李勇、方兆本和韦勇凤(2015)[13]提出了基于已实现波动率和Copula相结合的风险最小套期保值比率估计RV-Copula模型，对沪深300股指期货套期保值交易进行了研究。

近年来，随着小波变换技术的不断成熟，国内外很多学者将小波变换方法应用在金融时间序列分析领域。国外如In和Kim(2006)运用小波分析方法研究了期货和现货市场间的关联关系，并基于最小方差框架分析了期货最优套期比率问题。[14]Lien和Shrestha(2007)运用极大重叠小波变换将期货和现货收益率分解到不同的时间尺度上，再利用OLS回归方法得到不同时间尺度上的最优套期保值比率。[15]Conlon和Cotter(2012)基于小波变换并运用移动窗口最小二乘方法，研究了不同期限下期货最小方差套期保值比率和套期保值效率问题。[16]Khalfaoui、Boutahar和Boubaker同样运用小波方法，分析了原油市场和股票市场的关联关系和套期保值问题。[17]国内如王春峰等(2009)运用小波变换并研究了股指期货最小方差套期保值比率与套期保值期限的关系。[18]代军(2014)运用小波分析，研究期货与现货在不同时间跨度下的相互关系和套期保值比率。[19]

虽然上述研究丰富了运用股指期货进行套期保值的理论体系，为规避市场风险提供了很好的分析方法和工具，但据笔者所知，不同投资者对市场风险存在的认同感和对风险的偏好程度并不一致，因而他们采取的套期保值策略也会有所差异。鉴于此，本文首先通过把传统均值方差效用函数与风险厌恶系数相结合，构建不同风险偏好投资者的风险规避目标函数，然后借助小波分析方法和移动窗口技术，计算不同时间尺度和不同时刻的动态最优套期保值比，并就套期保值的有效性与传统均值方差风险准则下的避险效果进行了对比分析。这样可以为投资者进行风险规避提供更切实际的理论指导和符合不同投资者需求的个性化风险对冲策略。

二、模型、研究方法

(一)套期保值优化模型

如前所述，套期保值问题的核心是最优套期保值比的确定，而最优套期保值比又与套期保值优化目标函数有关，如常见的最小方差、均值-方差以及下方风险、VaR等目标函数。本文的主要目的是考虑不同投资者对风险的感知差异和风险偏好差异，寻求满足不同风险偏好投资者的风险对冲策略。对于投资者来说，他们是在自身风险承受能力的基础上追求投资收益的最大化，在此，我们借鉴均值方差目标函数并结合风险厌恶系数，构建期望效用目标函数作为最优套期保值比的确定依据。

假设投资者拥有一份多头股指现货资产，为了规避风险，投资者同时也在股指期货市场空头持有一定份额(套期保值比)的期货头寸，则以此构成的套期保值组合资产的收益率为：

rt=rs，t-htrf，t

(1)

其中，rs，t=ln(St+Δt/St)和rf，t=ln(Ft+Δt/Ft)分别是股指现货和股指期货在t时刻的收益率，ht表示t时刻的套期保值比。设E(rt)、var(rt)分别表示套期保值组合收益率的期望和方差，则期望效用函数可表示为：

E[U(rt)]=E(rt)-γvar(rt)

(2)

这里，γ(>0)表示投资者对风险的厌恶程度，γ越大，表示投资者对风险的厌恶程度越高。

最优套期保值比可以通过最大化EU(rt)来确定，即：

(3)

可以得最优套期保值比为：

(4)

其中，cov(rs，t，rf，t)表示股指现货和股指期货收益的协方差，E(rf，t)表示股指期货收益率的期望值，var(rs，t)、var(rf，t)分别表示股指现货和股指期货收益率的方差。显然，(4)式右边第二项反映投资者对风险的厌恶程度对套期保值比的影响，如果γ=，即投资者对风险无限厌恶，则(4)式右边退化为只剩第一项，即最小方差目标对应的最优套期保值比。显然，不同风险偏好投资者的套期保值策略有别于最小方差策略。本文将考虑风险厌恶程度与最优套期保值比的影响关系。

(二)套期保值效果

套期保值效果衡量的是套期保值操作对风险的降低程度。基于不同投资者的不同目标要求，关于套期保值效果的测度方法也多种多样。如Ederington(1979)提出了方差降低百分比度量方法[20]：

(5)

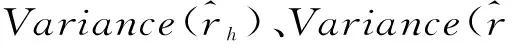
(6)

其中，γ表示投资者对风险的厌恶系数。

显然，无论是Ederington的方差降低百分比度量还是Lee的“均值-方差”效用度量法，都没有考虑对冲头寸调整产生的费用成本，事实上，头寸调整费用又是投资过程中不得不考虑的因素，尤其是对冲头寸调整频繁的情况下，可能导致一笔不菲的费用产生，而且对于各种投资者来说，他们关注的是投资期末的现实收益，因此，比较进行套期保值操作和不进行套期保值操作的投资收益，能更加直观地反映套期保值操作的效果。另外，我们假定投资者期初拥有一份多头股指现货资产，为了规避风险，同时也在股指期货市场空头持有一定份额(套期保值比)的期货头寸，以此构成套期保值组合，并在持有期结束时进行清仓。鉴于此，本文采用通过套期保值操作的组合资产的最终收益比不进行套期保值获得收益的增加额(见(7)式)表示套期保值的效果：

HE=[(ST-hT-1FT)-(S1-h1F1)-

hT-1FT)-[ST-S1]

=(1-f)*(h1F1-hT-1FT)

(7)

关于(7)式中的第一个等式，其第一部分表示进行套期保值操作的组合收益额，第二部分表示不进行套期保值的收益额。其中，ST和S1分别表示股指现货期末和起初价格，Ft和ht分别表示股指期货在时刻t的价格和股指期货(空头)头寸持有量，f表示股指期货交易费用率，根据当前中国金融期货交易所规定的沪深300股指期货交易费率，本文计算时取f=0.0115%。

(三)小波变换

本文旨在计算股指期货动态最优套期保值比及最优套期保值比与投资者对风险厌恶程度及套期保值期限的关系。从现有文献研究来看，关于套期保值比率的计算大多是基于某个模型假设或某种具体分布而展开，而模型或分布的假设具有主观性，必然导致研究结果的不理想。作为一种非参数方法，小波变换可以将一个数据信号分解成多个不同时间窗或不同频率成分，而且小波变换还可以克服诸如低频数据中的样本不足的缺陷，能够通过小波函数的伸缩与平移，对时间序列数据及其方差、协方差按不同期限进行分解，通过调整时频宽度，还能分析数据在各不同时频上的局部细节和方差、协方差在不同期限的变化特征，因而常常被用于时间序列研究。小波变换可分为连续小波变换和离散小波变换，基于金融时间序列本身的离散特征，通常采用离散小波变换方法更便于计算。为了克服普通离散小波变换要求样本数据的长度是2j的倍数的约束，在此，我们采用最大重叠离散小波变换方法(MODWT)[22]对股指期货套期保值问题展开研究。

假设φ(·)和ψ(·)分别表示父小波和母小波，则有∫φ(t)dt=1，∫ψ(t)dt=0。父小波描述信号或变量的低频部分，用于刻画变量的平滑性和趋势性，而母小波描述信号或变量的高频部分，它通过不同频率来刻画信号的细节变化。再定义如下伸缩因子为2的标准正交离散小波的基函数：

φj，k(t)=2-j/2φ(2-jt-k)

(8)

ψj，k(t)=2-j/2ψ(2-jt-k)

(9)

其中，j=1，2，…，J表示小波分量的个数，即根据数据长度决定的最大尺度，j越大表示分量越多，对应的频率越低，信号变换越粗糙。J表示小波分解水平。k表示频率确实时的小波变换次数。这样，对于离散信号f(t)，其小波多分辨函数可表示为：

(10)

其中，sJ，k=∫φJ，kf(t)dt，dj，k=∫ψj，kf(t)dt

(j=1，2，…，J)

对于任意时刻t和分解水平j，极大重叠离散小波变换能生成一系列小波系数和尺度系数：

(11)

(12)

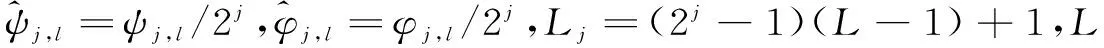
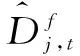
(13)

(14)

特定尺度上的小波方差反映其对样本方差的贡献，类似地，小波协方差也反映出两个不同序列间的协方差。我们可以据此进行套期保值比率的确定。

三、实证分析

(一)数据处理

考虑到我国目前仅有沪深300股指期货上市交易，所以本文采用沪深300股指的每日收盘价作为现货价格，同时考虑到期货合约的流动性，采用临近到期的沪深300股指期货合约的日收盘价作为期货价格。样本区间均为2010年4月16日(沪深300股指期货上市时间)至2015年10月31日，共1342对日数据。其中2010年4月16日至2014年12月31日的1142对数据作为样本内数据，即起始滚动窗口数据用于计算套期保值比率，2015年1月1日至2015年10月31日的200对数据作为样本外数据，用于套期保值效果的评价。数据来源为国泰君安睿智版软件提取。

图1表示的是沪深300指数和沪深300股指期货主力合约日收盘价格走势，由图1可知，两者走势基本一致，利用沪深300期货能够对沪深300指数进行套期保值的风险对冲操作。对沪深300股指和期指的对数收益率序列分别做正态性、平稳性和异方差性检验，结果(见图2和表1)表明各类检验在1%的置信水平下均拒绝了原假设，即两个对数收益率序列平稳但不服从正态分布，而且从图2的统计结果可知，沪深300股指期货的波动率略大于沪深300指数的波动率，即期货市场的波动性更大一些。所有计算均在Eviews8.0软件中实现。

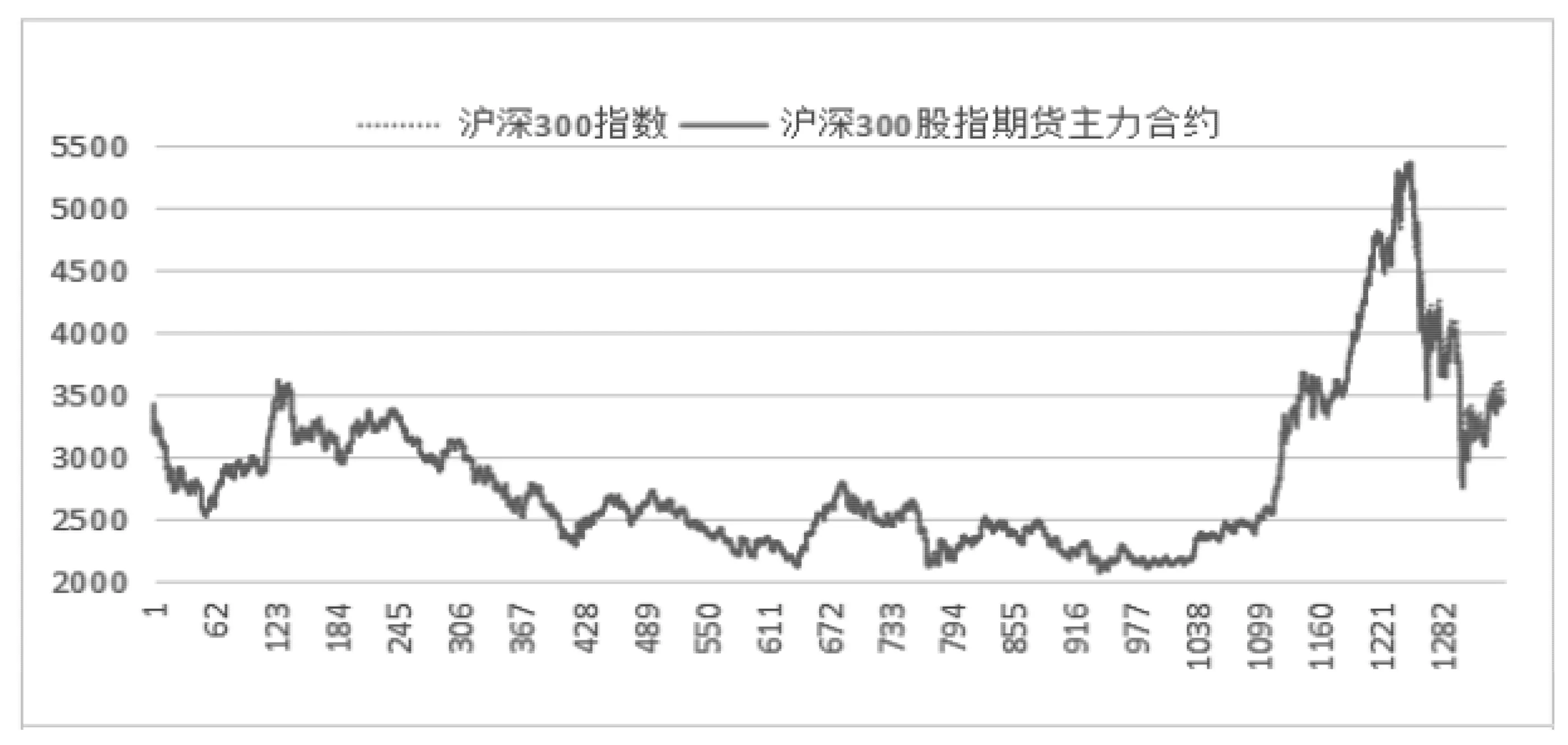
图1 沪深300指数收盘价和沪深300股指期货主力合约收盘价

图2 沪深300股指(上)和沪深300期指(下)对数收益率的统计特征

表1 沪深300股指(上)和沪深300期指(下)对数收益率的单位根检验

(二)套期保值比率

本小节中，我们采用MODWT方法对沪深300指数和沪深300股指期货收益率进行小波分解，并计算不同风险偏好投资者在不同套期保值期限下的套期保值比率。对时间序列进行小波分析，小波滤波器的选择极为重要，滤波器的选取与数据信号本身的特征和数据长度有关。考虑到本文样本数据长度和滚动窗口长度，我们选择LA8小波滤波器，并且最大分解层数为6层。对数据序列进行小波分解后，考虑到各尺度上的小波方差之和反映其对样本方差的贡献，类似地，小波协方差也反映出两个不同序列间的协方差。因此，我们只需根据(13)式、(14)式计算的小波方差和小波协方差替代(4)式中的序列方差和协方差。对于(4)中的股指期货未来收益率的期望值，即E(rf，t)，我们借鉴梁强等[23]和王书平等[24]的方法，利用小波多尺度分析的功能，根据股指期货时间序列预测其未来长期走势。所有这些计算均无需依赖价格或收益的分布，也不需要对价格或收益进行模型构建，因而计算结果更能反映时间序列的本质特征。然后再结合窗口滚动技术，计算得到不同套期保值期限和不同风险偏好下的动态最优套期保值比率。

图3是不同套期保值期限和不同风险偏好对应的套期保值比率变化图。首先，由图可知，资产持有期即套期保值期限越长、距离到期日越远，需要持有的期货(空头)头寸越大。同时也可以发现，随着到期期限的临近，持有的对冲头寸随之减少。其次，随到期日的临近，对冲头寸保持降低趋势的同时，偶尔也有反弹现象，对比动态套期保值比率变化图上的反弹点和该时刻的股指现货价格可以发现，对冲头寸反弹点基本与股指现货价格明显下跌的时刻相对应。譬如以图3(上)为例，其中就有几个较为明显的头寸反弹点，这些点正是对应指数现货价格由3886.13元跌至3025.69元，对冲头寸则由0.8455反弹至0.8515。对冲头寸的这些变化特征反映出对冲期限、价格波动与市场风险之间具有相伴关系，期限越长、距离到期日越远、价格波动越大，可能面临的风险也越大，要达到同样的风险对冲目的则需要持有的对冲头寸也就越高。事实上，金融市场风险的本质也就是价格波动，持有某种金融资产的时间越长，价格发生大幅波动的概率越大，体现出来的风险也越大。另外，由图3也可以知道，无论套期保值期限长短与否，对冲头寸与投资者对风险的厌恶程度均有关。总体而言，对风险的厌恶程度越高，持有的对冲头寸也越多。这主要是因为对风险高度厌恶的投资者来说，他们首先考虑规避风险，然后才考虑收益的高低。正如Keynes和Hicks所说，“金融衍生品市场参与者出于风险厌恶的本性，希望通过套期保值来完全消除与某一特定商品有关的价格风险，因而最优的风险对冲策略就是保持套期比恒为1”[4，5]。但是，当投资者的风险厌恶程度增大到一定限度时，对冲头寸受风险厌恶的影响会随之降低，这一关系可以通过对比图3中不同风险厌恶程度(risk aversion)的对冲头寸变化而发现。由图可知，对三种不同套期保值期限而言，风险厌恶系数为1时的对冲头寸明显低于其他高风险厌恶系数下的对冲头寸，然而，风险厌恶系数为50和100的情况下，对冲头寸就相差甚微了。

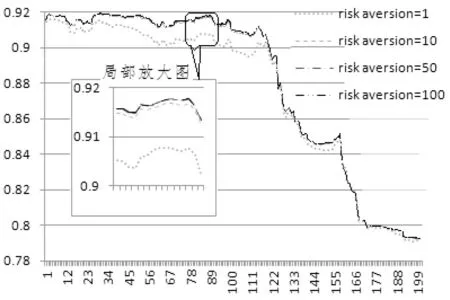
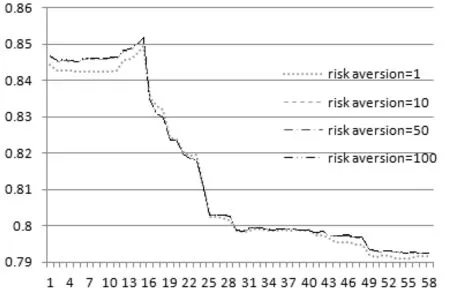
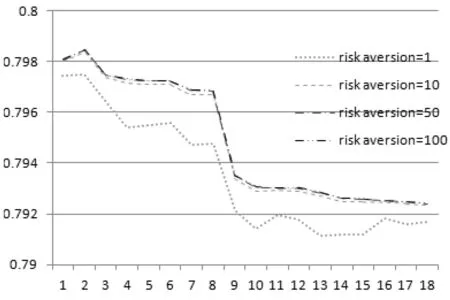
图3 股指期货动态套期保值率(上：套期保值期限为10个月；中：套期保值期限为3个月；下：套期保值期限为1个月)

(三)套期保值效果

为了判断套期保值操作的有效性和比较套期保值的有效程度，本文提出如(7)式所示的一个比较直观而又现实的测度指标HE来衡量套期保值效果。该指标值越大，表示套期保值效果越好。图4是通过小波变换和滚动窗口方法计算得出的动态套期保值效果变化情况。

首先，根据套期保值效果变化图可以看出，利用股指期货进行套期保值操作的收益普遍要好于不进行套期保值操作的投资收益。事实上，在图4所示的检验期内，套期保值效果指标值HE大于零的概率都在0.6以上，而且无论套期保值期限长短与否，无论风险偏好情况如何，指标HE的平均值均大于零(见表2)。

其次，由图4可知，无论是哪种套期保值，对不同风险偏好情况下的套期保值效果曲线图十分相似，即套期保值效果具有很高的相似性。而且由表2的指标值可以发现，投资者的风险偏好程度也影响着套期保值效果，相对于风险偏好型投资者来说，风险厌恶型投资者因为采用更高的对冲比率，因而通过套期保值操作的效果越好，即获取的收益越高，这与我们前面对套期保值比率的分析相一致，也与Keynes[4]和Hicks[5]的结论相吻合。

另外，由表2也可以发现，风险偏好对短期套期保值效果的影响程度要高于对较长期的套期保值效果。譬如对于1个月套期保值期限来说，风险厌恶系数的增加显著影响套期保值的效果，而对于3个月和10个月期的套期保值而言，风险厌恶系数的改变对套期保值效果的影响相对较弱。

最后，从三种不同期限套期保值操作的效果来看，无论风险偏好程度如何，三个月期的效果均高于其他两种期限的套期保值效果。实际上，因为套期保值过程中交易费用的存在，长期的、频繁的头寸调整会引起一笔不菲的交易费用，这最终会影响到投资的总收益，即套期保值效果。

总之，对于投资者来说，风险是一个必须考虑的因素，可以通过套期保值操作来降低风险，但套期保值实践中关于对冲头寸的建立和调整，要适当考虑自身的风险承受能力、风险偏好程度、投资期限的长短和各种费用的存在情况。

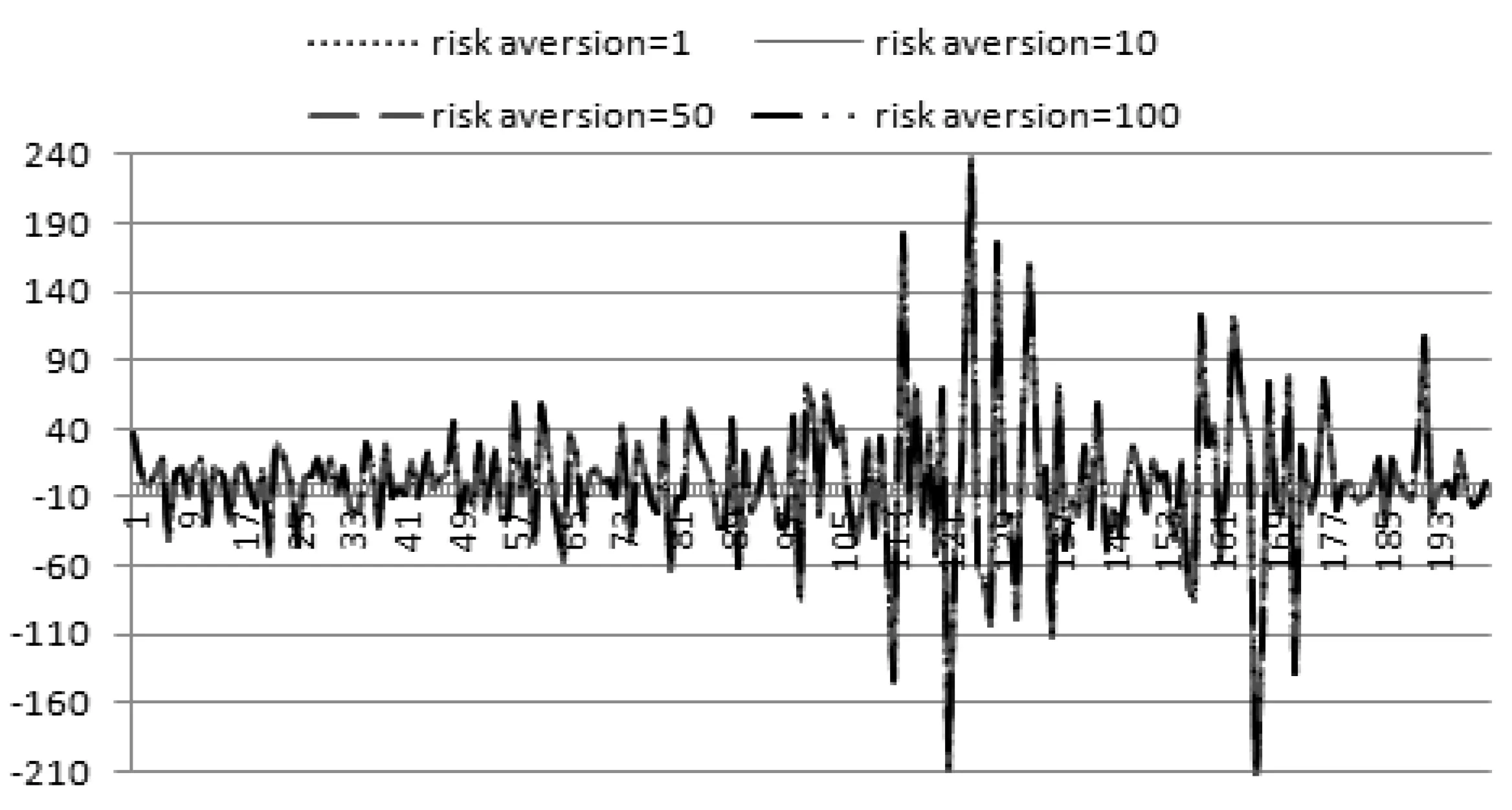
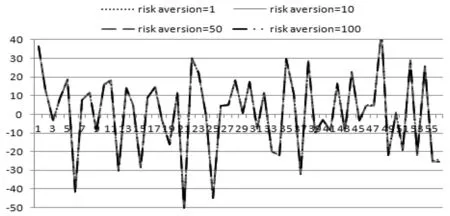
图4 套期保值效果变化图(套期保值期限，上：10个月；中：3个月；下：1个月)

表2 套期保值效果评价指标(HE)值

四、结论

股指期货除了作为一种投资工具存在外，更主要的功能是用于风险规避。利用股指期货进行套期保值的目的就是规避价格波动风险，合理的套保策略是既达到保值目的又节约资源的关键。本文运用小波变换方法，研究了沪深300股指期货的最优套期保值策略，分析了最优套期保值比、套期保值效果与投资者的风险偏好、套期保值期限的关系。通过本文的实证研究，得到如下结论：

(1)套期保值期限越长，可以考虑采用较高的套期保值头寸，有利于风险规避。但因为交易费用的存在，对于动态套期保值而言，期限越长，需要的头寸调整费用越高，套期保值组合的最终收益未必最高。

(2)风险厌恶型投资者通常采用较高的对冲头寸进行风险规避，风险对冲效果也越好；反之，投资者对风险的偏好程度越高，可能采用的风险对冲头寸越低，套期保值的效果也相对较低。

(3)短期的套期保值效果受投资者对风险的偏好程度的影响较长期套期保值更明显，套期保值期限越短，风险偏好程度对套期保值效果影响越显著。

总之，对于投资者来说，风险是一个必须考虑的因素，因为市场是千变万化的，可以通过套期保值操作来降低风险，要得到好的套期保值效果，不仅需要良好的策略方案支撑，也需要根据实际情况做出策略调整以应对市场的改变。在套期保值实践中，关于对冲头寸的建立和调整，要同时考虑自身的风险承受能力、风险偏好程度、投资期限和各种费用的存在情况。

[1]徐国祥，檀向球.我国A股市场系统性风险的实证研究[J].统计研究，2002，(5)：37-40.

[2]Schrand C，Unal H.Hedging and Coordinated Risk Management：Evidence from Thrift Conversions[J].The Journal of Finance，1998，(3)：979-1013

[3]谢赤，屈敏，王纲金.基于M-Copula-GJR-VaR模型的黄金市场最优套期保值比率研究[J].管理科学，2013，(2)：90-99.

[4]Keynes J M.Alternative theories of the rate of interest[J]．The Economic Journal，1937，(186)：241-252．

[5]Hicks J R．A suggestion for simplifying the theory of money[J]．Economica，1935，(5)：1-19．

[6]Johnson L L.The theory of hedging and speculation in commodity futures[J]．The Review of Economic Studies，1960，(3)：139-151．

[7]Ederington L H．The hedging performance of the new futures markets[J]．The Journal of Finance，1979，(1)：157-170．

[8]Hsu C.C，Wang Y.H，Tseng C.P.Dynamic hedging with futures：A copula-based GARCH model[J].Journal of Futures Markets，2008，(6)：156-168.

[9]马超群，王宝兵.基于Copula-GARCH模型的外汇期货最优套期保值比率研究[J].统计与决策，2011，(12)：124-128.

[10]谢赤，屈敏，王纲金.基于M-Copula-GJR-VaR模型的黄金市场最优套期保值比率研究[J].管理科学，2013，(2)：90-99.

[11]代军，朱新玲.沪深300股指期货对冲效率研究[J].中国管理科学，2014，(04)：1-8.

[12]彭红枫，陈奕.中国铜期货市场最优套期保值比率估计——基于马尔科夫区制转移GARCH模型[J].中国管理科学，2015，(5)：14-22.

[13]李勇，方兆本，韦勇凤.风险最小化套期保值比例估计：基于RV-Copula模型[J].数理统计与管理，2015，(2)：15.

[14]In F，Kim S.The hedge ratio and the empirical relationship between the stock and futures markets：A new approach using wavelet analysis[J].The Journal of Business，2006，(2)：799-820.

[15]Lien D，Shrestha K.An empirical analysis of the relationship between hedge ratio and hedging horizon using wavelet analysis[J].Journal of Futures Markets，2007，(2)：127-150.

[16]Conlon T，Cotter J.An empirical analysis of dynamic multiscale hedging using wavelet decomposition[J].Journal of Futures Markets，2012，(3)：272-299.

[17]Khalfaoui R，Boutahar M，Boubaker H.Analyzing volatility spillovers and hedging between oil and stock markets：Evidence from wavelet analysis[J].Energy Economics，2015，(49)：540-549.

[18]王春峰，张龙斌，房振明.股指期货对冲比率和对冲期限关系的多尺度研究[J].系统工程理论与实践，2009，(1)：6-12.

[19]代军.沪深300股指期货与现货的相关性及对冲比率研究—基于小波多尺度分析[J].湖北社会科学，2014，(12)：90-95.

[20]Ederington L H.The hedging performance of the new futures markets[J].The Journal of Finance，1979，(1)：157-170.

[21]Lee H T.Optimal futures hedging under jump switching dynamics[J].Journal of Empirical Finance，2009，(3)：446-456.

[22]Gençay R，Selçuk F，Whitcher B J.An introduction to wavelets and other filtering methods in finance and economics[M].Academic press，2001.

[23]梁强，范英，魏一鸣.基于小波分析的石油价格长期趋势预测方法及其实证研究[J].中国管理科学，2005，(1)：30-36.

[24]王书平，胡爱梅，吴振信.基于多尺度组合模型的铜价预测研究[J].中国管理科学，2014，(8)：21-28.

The Optimal Hedging Strategies of Stock Index Futures Based on the Investor’s Risk Aversion

GUO Jian hua

(Department of Economics and Management， Shaoyang University， Shaoyang 422000， China)

Investors can avoid financial risk by hedging with stock index futures. However， because of the investor’s different degree of risk aversion， their hedging strategies may be different from each other. This paper firstly constructs objective functions by combining the utility function with coefficients of risk aversion for different investors. Then it calculates the optimal dynamic hedging ratios by using wavelet transform method and analyzes the relationship between the optimal hedging ratios， the hedging effectiveness， the level of risk aversion of investor and the hedging horizon. It turns out that the lower the risk aversion level of investors is， the smaller hedging ratios may be adopted but with lower hedging effectiveness; the further the hedging horizon is， the greater the optimal hedging ratios will be.

risk aversion; stock index futures; hedging strategies; wavelet analysis

2016-07-10

教育部人文社会科学研究青年基金项目(15YJC630026)；湖南省教育厅资助科研项目(14B160)

郭建华(1975-)，男，湖南邵阳人，邵阳学院经济与管理系副教授，经济学博士。

F830.91

A

1672—1012(2016)05—0093—10