量子态的局部酉等价分类问题研究

孙 欢

(渭南师范学院 科学技术处，陕西 渭南 714099)



【自然科学基础理论研究】

量子态的局部酉等价分类问题研究

孙 欢

(渭南师范学院 科学技术处，陕西 渭南 714099)

讨论了在量子态局部酉等价(LU等价)条件下系统密度矩阵的有关性质，包括密度矩阵的秩、特征值及奇异值的关系，得到了两个态LU等价的充分必要条件是两者的核心张量相同或仅相差具有特定结构算子。

密度矩阵；局部酉等价；奇异值

众所周知，量子态的等价分类问题研究已经成为量子计算和量子通信领域中的一个重大课题。近年来，在量子态的等价分类问题上，不论是对多体量子态纯态等价的讨论，还是对多体量子态混合态等价的讨论，相比以前都取得了极大进步[1]。本文在符合量子力学假设前提条件下，针对量子态的局部酉等价(LU等价)有关问题，讨论了满足两个局部酉等价的量子态所对应密度矩阵满足的条件，并且通过向量的n指标矩阵表示的定义给出了量子态的n指标矩阵表示，最后得到了量子态局部酉等价所满足的条件和定理，通过举例证实了结论的正确性。

1 量子态的LU等价

其中：Ui(i=1,2,…,n)是Hi上的酉算子。

(1)ρφ=UρψU+(U为酉阵)，且ρψ,ρφ的奇异值相同；

我们知道，对于一个封闭的量子系统，它的演化是由一个酉变换来描述的，即系统在时刻t1的状态ρ1和时刻t2的状态ρ2由一个仅依赖于时间t1,t2的酉算子联系：ρ2=U(t1,t2)ρ1U(t1,t2)+，即LU等价的量子态也可以看作是一个封闭量子系统演化下不同时刻的态。

定义2给出了矩阵到向量之间的映射，容易验证对于两体量子态，通过这样的映射，把两个态|a〉和|b〉的外积转换成了|a〉和|b〉的张量积的形式，对于两体量子态的矩阵表示，记为f-1(|ψ〉)=ψ。

通过上述定义，给出定理：

|φ〉 =U2⊗V2|S2〉=(U2⊗V2)|S1〉

=(U2⊗V2)(U1⊗V1)+|ψ〉=U2U1+⊗V2V1+|ψ〉，

下面通过例题验证LU等价的量子态所符合的条件和性质。

例1 Bell态均是LU等价的[4]。

证明 Bell态对应的矩阵表示和奇异值分解分别为：

可以看到，Bell态所对应的矩阵表示具有相同的奇异值，由定理1的结论可以得到 Bell态均是LU等价的。

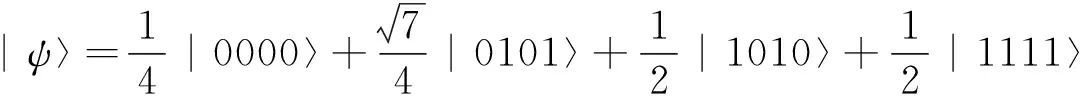
令

2 多体量子态的分类

定理2说明了两体态LU等价的充要条件，我们用多维张量积的奇异值分解[5]来研究多体态的LU等价问题。

定义3 对A∈CI1×I2×…×IN，定义矩阵An∈MIn×(In+1In+2…INI1I2…In-1)，即对应In行In+1…INI1…In-1列矩阵，其中An矩阵中的元素ai1i2…iN位于An的第in行第(in+1-1)In+2…INI1…In-1+…+(iN-1)I1…In-1+

(i1-1)I2…In-1+(i2-1)I3…In-1+…in-1列，称An为A的n指标矩阵表示。

例3 设A∈R3×2×3，其中

a111=a112=a211=-a212=1，a223=a321=a323=4，

a113=a312=a123=a322=0，a121=a122=a213=a221=-a222=a311=a313=2。

对应的矩阵表示分别为

定理2 (多维张量积的奇异值分解定理)设A∈CI1×I2×…×IN，则有下式成立：

其中：U(n)是一个In×In酉阵，A×nU为A的n模积，S∈CI1×I2×…×IN且满足以下条件：

(1)〈Sin=α,Sin=β〉=0(α≠β，Sin=α表示固定第n个指标为α)；

(2) ‖Sin=1‖≥‖Sin=2‖≥…≥‖Sin=IN‖≥0,(n=1,2,…，N)，其中：S称为A的核心张量。

可以看到定理2使用起来比较复杂，通过定义3中的矩阵表示可以给出下面的等价关系式：

An=Un·Sn·(Un+1⊗Un+2⊗…UN⊗U1⊗…⊗Un-1)T。

由定理2对多体态|ψ〉有下式成立：

ψn=Un·Sn·(Un+1⊗Un+2⊗…UN⊗U1⊗…⊗Un-1)T。

故|ψ〉∈C2⊗C2⊗C4的核心张量为

引理1 若|ψ〉=⊗nUn|S〉且|ψ〉=⊗nVn|S'〉，则|S'〉=⊗nQn+|S〉，其中：Qn具有例2中U1，U2的形式，即Qn是与|ψ〉的n指标矩阵表示的奇异值结构一致的分块对角酉阵。

证明 因为|ψ〉=⊗nUn|S〉，由向量的n指标矩阵表示定义知有下式成立：

ψn=Un·Sn·(Un+1⊗Un+2⊗…UN⊗U1⊗…⊗Un-1)T。

又由于|ψ〉=⊗nVn|S'〉，有下式成立：

故有下式成立：

|ψ〉=⊗nWn|S〉,|φ〉=⊗nVn|S'〉。

由条件知|ψ〉=⊗nUn+|φ〉=(⊗nUn+)(⊗nVn)|S'〉，由引理1得|S'〉=⊗nQn+|S〉。

充分性：设|S'〉=⊗nQn+|S〉，对|ψ〉,|φ〉进行多维张量的奇异值分解得：

|ψ〉=⊗nWn|S〉=(⊗nWn)(⊗nPn)|S'〉，

|φ〉=⊗nVn|S'〉。

则有下式成立：

即|φ〉=⊗nUn|ψ〉。

3 结语

本文主要讨论了量子态的LU等价问题，通过量子系统的密度矩阵和量子态的矩阵表示方法，得出了两个态LU等价所满足的条件和定理，证明了两个态LU等价的充要条件是它们的核心张量相同或仅相差具有特定结构的算子。

[1] M. Walter,B. Doran,D. Gross,et al.Entanglement polytopes: multiparticle entanglement from singleparticle information[J].Science，2013,340(6137):1205-1208.

[2] Michael A.Nielsen,Isaac L. Chuang.量子计算和量子信息[M].北京：清华大学出版社，2009.

[3] David W. Lyons, Scott N. Walck. Multiparty quantum states stabilized by the diagonal subgroupof the local unitary group[J].Phys.Rev.A,2008,78(4):042314.

[4] W.Dur,G.Vidal,J.I.Cirac. Three qubits can be entangled in two inequivalent ways[J].Phys.Rev.A,2000,62(6):062314.

[5] T.Bastin,S.Krins,P.Mathonet,et al.Operational families of entanglement classes for symmetric n-qubit states[J].Phys.Rev.Lett,2009,103(7):070503.

【责任编辑 牛怀岗】

A Research on Classification of Quantum States under LU Equivalence

SUN Huan

(Department of Science and Technology,Weinan Normal University,Weinan 714099,China)

This paper discusses the properties of density matrix of multi-partite quantum states on local unitary equivalence, including the rank, eigenvalue and singular value of density matrix. Especially, it is proved that two states are local unitary equivalence if and only if their core tensors are the same or differ by a specific structure of the operator.

density matrix; local unitary equivalence; singular value

O177.1

A

1009-5128(2016)19-0019-05

2016-08-21

国家自然科学基金项目:量子态分类与量子绝热逼近中的算子论方法(11371012)

孙欢(1989—)，女，陕西大荔人，渭南师范学院科学技术处教师，理学硕士，主要从事量子信息与量子计算研究。