认知无线电快速时域能量检测方法*

何健标

（深圳职业技术学院 电子与通信工程学院，广东 深圳 518055）

认知无线电快速时域能量检测方法*

何健标

（深圳职业技术学院 电子与通信工程学院，广东 深圳 518055）

提出一种快速时域检测方法，该方法基于下变频器和低通滤波器的并行检测结构，通过共享多相滤波器组，以及采用快速反傅里叶变换模块替换下变频器的方法，实现并行检测的快速计算.通过仿真实验对比，证明本算法在检测误差、计算成本等方面比传统的时域或频域能量检测方法性能更好.

认知无线电 频谱感知 时域能量检测 快速算法

认知无线电（Cognitive Radio，CR）能感知周围环境并通过实时改变传输功率、载频、调制方式等传输参数来适应环境的变化，其实现关键在于无线电空闲频谱的感知.频谱感知方法根据算法类型可分为匹配滤波检测、能量检测、循环平稳检测和特征值检测等4类方法[1].其中能量检测类方法具有适用范围广、计算成本低、检测时间短等优点，是应用最为广泛的频谱感知技术.

能量检测根据外部无线电信号的能量谱分布，通过提取目标频段的特征参数辨识是否存在授权用户或其他CR用户.辨识判决方法包括单门限方法[2]、双门限方法[3]、滞回门限方法[4]和双阙值方法[5]等；由于噪声的影响，上述方法中检测门限的计算和优化需要估计噪声功率的分布[6-8]，而文献[9，10]根据序贯检测模型通过多次判决结果的融合改善信道占用辨识的虚警概率和漏警概率.有限检测时间的能量谱分布等同于功率谱检测，可以在时域[11]或频域实现（见图1）.频域能量检测的实质是根据周期图方法直接计算信号的功率谱，可借助FFT运算实现快速的并行检测，实时性好分辨率高；缺点是受信号截断影响大，信号泄露现象严重，检测误差较大.时域能量检测方法误差小、精度高；但是没有快速并行计算方法，导致计算复杂，无法实现高分辨率检测.

本文针对时域能量检测的快速实现方法进行研究，讨论了并行检测模型，研究并行检测的快速实现方法，比较了算法的检测性能和计算成本.

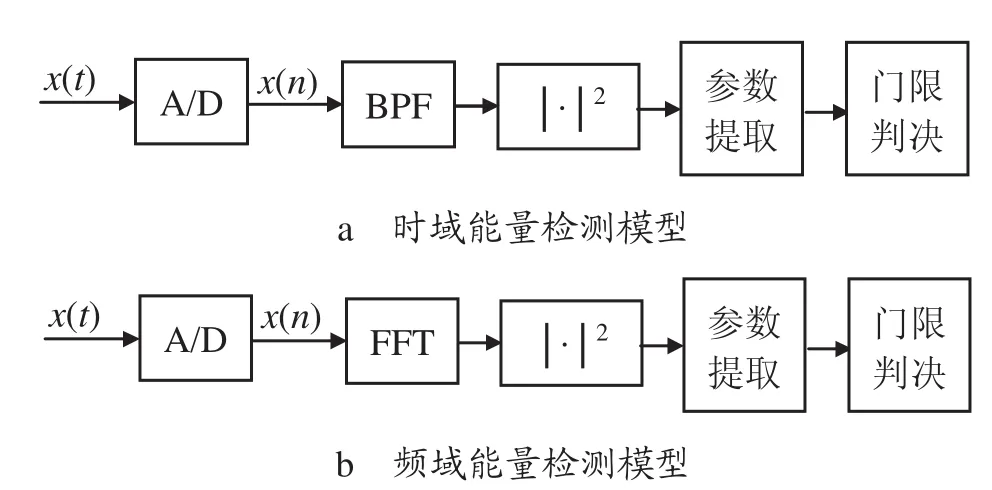
图1 能量检测模型

1 并行检测模型

根据图1a中的时域能量检测模型，其计算过程可描述如下：

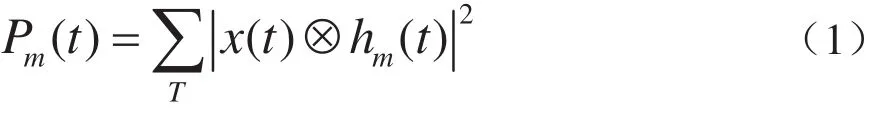
其中，hm(t)是第m个频点的带通滤波器，负责抑制待测频点之外的信号分量；图1b频域能量检测方法中待检测信号x(n)通过快速离散傅里叶变换（FFT）可以并行同时计算M个频点的信号功率.两者相比，图1a中的时域能量检测方法根据带通滤波器hm(t)的通带频率每次计算一个频点的信号功率Pm，属于串行检测，计算效率较低.如需在时域并行计算M个频点的信号功率，可将图1a改写成图2 所示的时域能量并行检测模型：x(t)是待测模拟信号；x(n)是x(t)采样量化得到的数字信号；采样频率为FS，则第m个频点在nTS时刻的能量检测结果Pm可由下式计算获得：式中，T是信号采集时间；h(i)是FIR数字低通滤波器的时域冲激响应，其幅频响应的截止频率fstop以及各并行支路子载波频率ωm由下式确定：

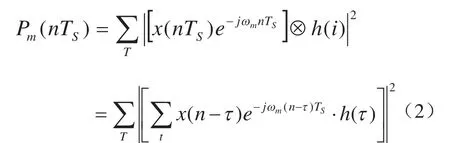
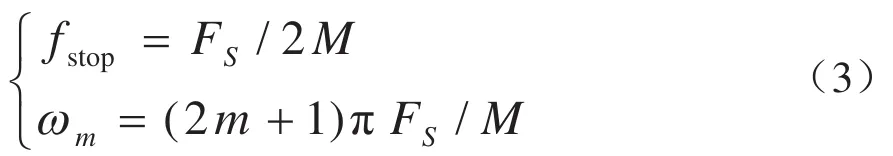
图2所示的时域能量检测并行计算模型是通过图1b中串行时域检测模型复制M个支路获得，算法复杂度为O(M2)，与频域检测方法复杂度O(MlogM)相比，在M较大时其计算量急剧上升，因此该并行模型不适用于高分辨率检测，需要在该模型的基础上研究快速方法实现高分辨率检测.

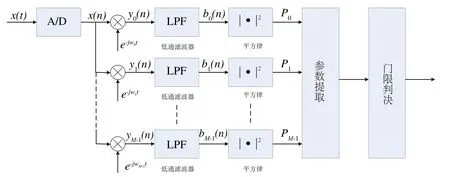
图2 并行时域能量检测模型

2 快速检测方法

根据图2的并行检测模型，以式（3）定义的子载波频率代入式（2）并化简，则m频点nTS时刻的能量Pm，其检测计算过程可描述如下：

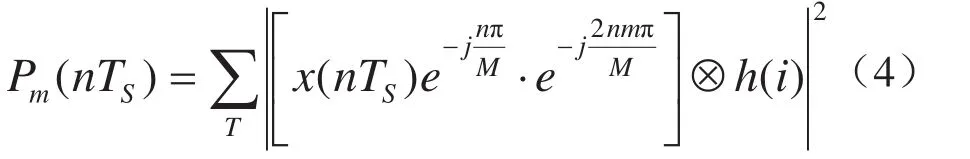
为简化检测的计算过程，定义一个新的序列x’(n)，由x(n)与正交载波相乘获得，即：

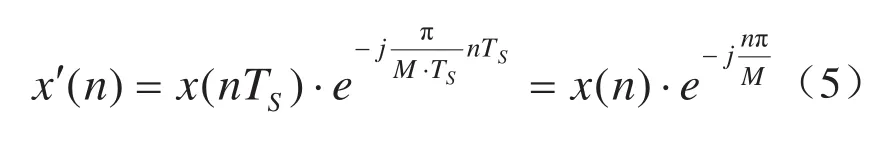
根据傅里叶变化的性质，x’(n)的频谱由x(n)频移FS/(2M)获得，则式（4）可改写成：

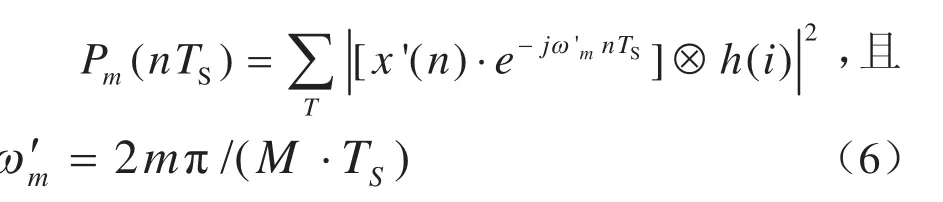
式（6）中能量的检测计算采用正交检测，载波相位不影响最终检测结果.因此实际检测中可以不使用绝对时间零点作为相位原点，而是以计算功率的时间点nTS作为载波相位原点，这样可以省略载波相位计算等步骤，即：

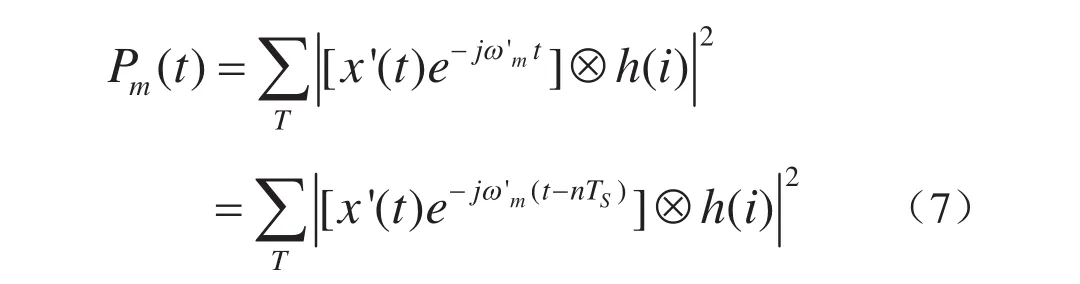
对应于nTS的检测时刻，可改写成：

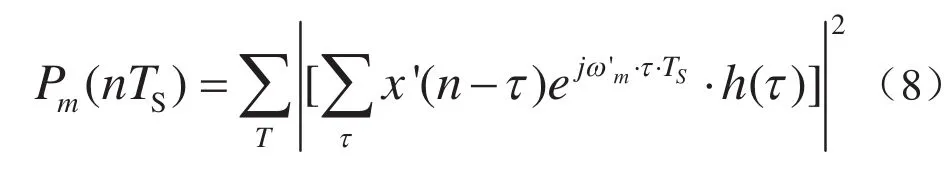
为了便于在后续章节与基于周期图的频域能量检测方法比较讨论，将能量检测的信号采集时间T分割成L个单位时间段，单位时间段的时长为MTS，即：

其中，L是单位时间段的个数，应为自然数.该条件可以通过调整数字信号采样率、检测分辨率以及信号采集时间等参数得到满足，或者直接在信号序列尾部添零补齐，则式（8）可改写成：

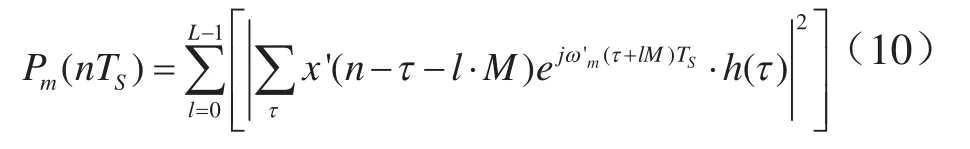
检测信号x’(n)经过M个频点的正交载波变频后再通过统一的低通滤波器h(i)，这一信号处理过程是整个检测算法中计算最为复杂的部分，因为经过变频后M个频点有M路信号需要分别经过低通滤波器h(i)，所以算法复杂度是O(M2).而M个支路的低通滤波器完全相同，如能使各支路共享该低通滤波器，则算法复杂度可降为O(M)，将低通滤波器h(i)分解成M个通道的多相滤波器组：

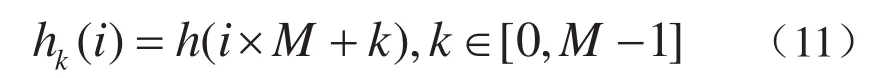
将hk(i)和'mw代回式（10），并化简：

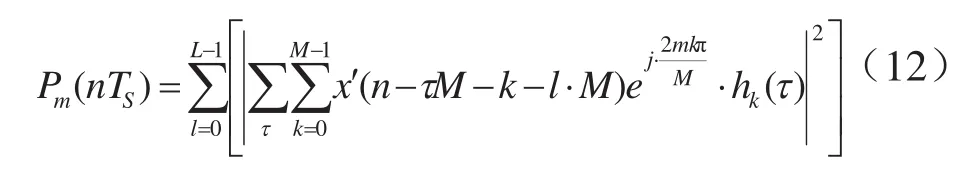
交换积分顺序不影响最终的计算结果，并将与t无关的公因数提取，即：

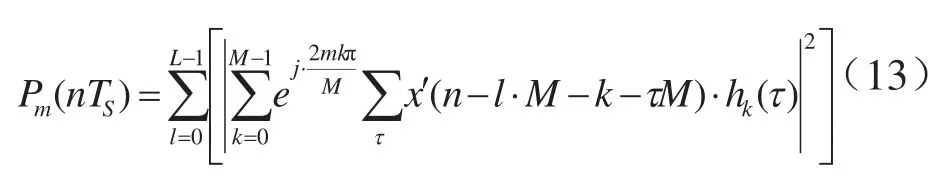
经过交换积分顺序并提取公因数，检测信号x’(n)不需要经过正交变频后再通过多相滤波器组，而是先通过hk(i)再作后续信号处理.换言之M个支路的信号不需要单独通过滤波器h(i)，而是可共享多相滤波器组hk(i)，该过程算法复杂度降为O(M)，与原算法相比可大幅提升并行计算效率.

再将y’k(n)定义为x’(n)通过hk(i)的输出：

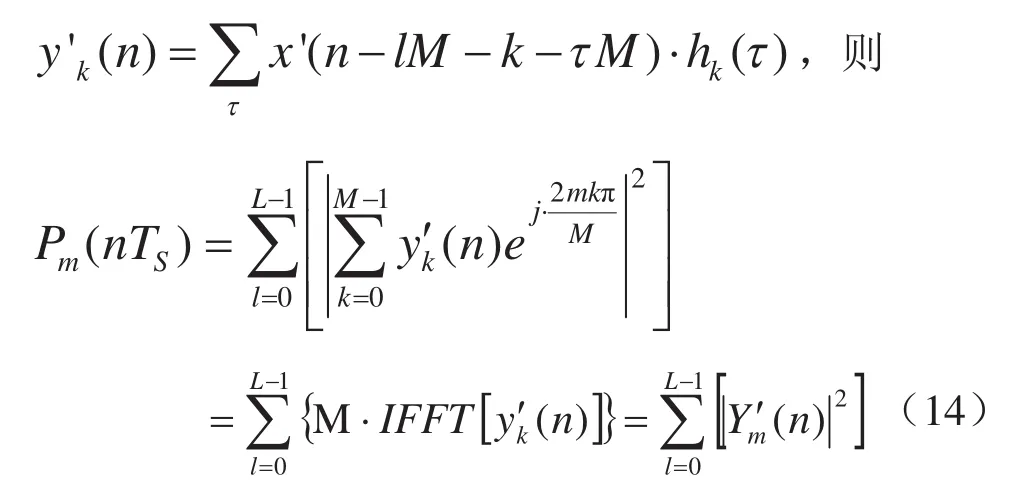
其中，Y’m(n)是y’k(n)作M点反傅里叶变换的结果，可利用蝶形算法实现Y’m(n)的快速并行计算，相当于用IFFT计算替代原算法中的载波合成与变频运算，可将该信号处理过程的算法复杂度降为O(MlogM).

综合以上信号处理过程，快速检测方法可用图3描述：待测信号x(t)经过采样量化、正交变频后得到x’(n)，然后通过多相滤波器组hk(i)得到y’k(n)，经过IFFT运算求得Y’m(n)，最后取模并根据信号采集时间求和即获得对应频点的能量.其中复数变频、多相滤波器组、取模以及序列求和等信号处理过程的算法复杂度都是O(M)，IFFT过程的算法复杂度是O(MlogM)，因此快速时域能量检测方法的算法复杂度与基于周期图的频域能量检测方法一样也是O(MlogM).

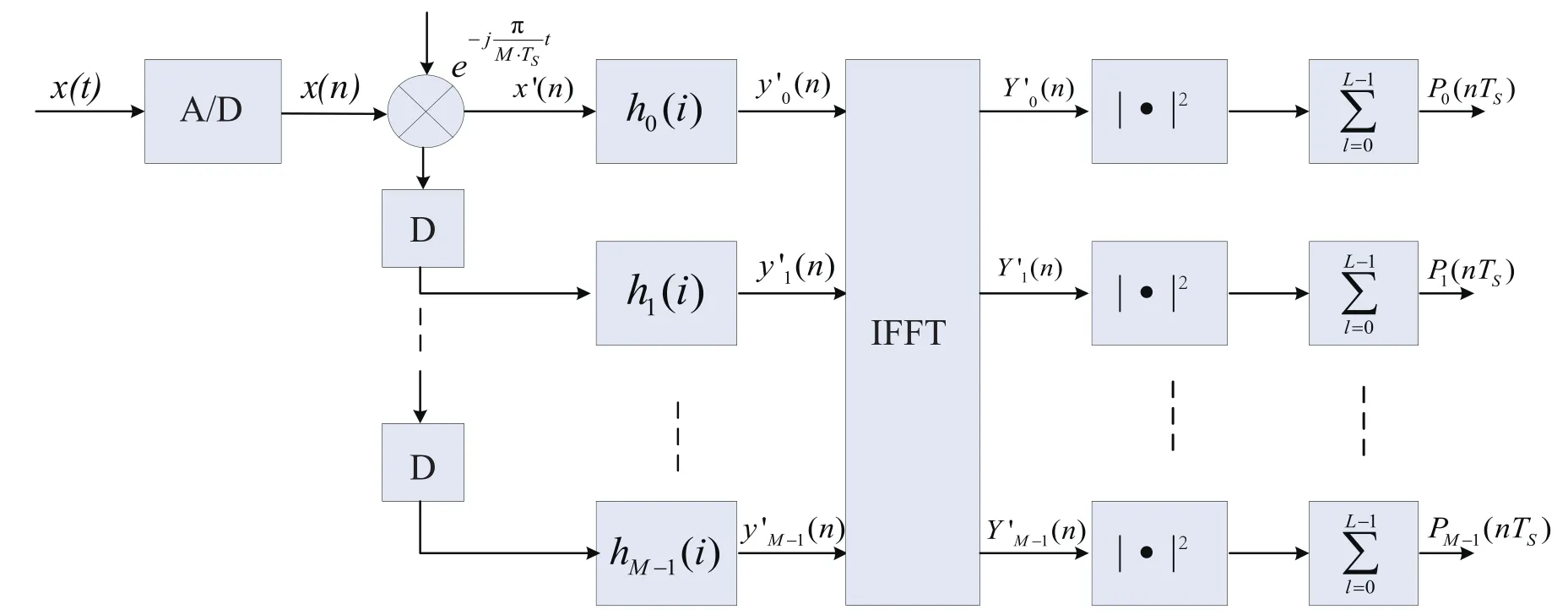
图3 快速时域能量检测方法

3 性能分析

3.1 仿真实验一

本实验利用Matlab搭建仿真环境验证能量检测算法性能的实验过程如下：

1）模拟合成待测信号.为避免数字信号的抽样混叠影响检测性能的对比，待测信号采用理想的带限信号，由若干个离散频率的单音信号叠加而成.待测信号合成的参数如表1所示，共有21个单音（频）信号，均匀的分布在40~50 MHz之间，每500 kHz有一个信号.

2）统一功率检测算法的参数便于不同算法的性能对比.所有功率检测方法都统一采用128MHz的频率对待测信号进行采样，信号采集时间为2µs，检测频率范围为39~53MHz，检测分辨率为500kHz，共计检测29个频点（见表1）.

3）采用本文所述算法和传统频域周期图法，按照表1的分析检测参数分别计算待测信号的功率，两种检测方法在 39-53MHz的频率范围内共计检测29个频点（其中21个频点存在信号）.

4）检测结果的对比.在“功率-频率”坐标系中，针对29个检测频点分别显示实际信号功率和2种检测算法的结果：部分待测频点（21个）的频率范围内有一个单音信号，该信号功率即为该频点的实际信号功率，在图中用离散“*”点符号表示；为以示区别，本文所述算法和频域周期图法的测量结果（功率）分别用实线和虚线将29个离散点连成折线.因此折线与离散“*”点偏离越大，说明该折线对应算法的检测结果偏差越大；反之折线若能与“*”点重合，说明该频点检测结果偏差极小.

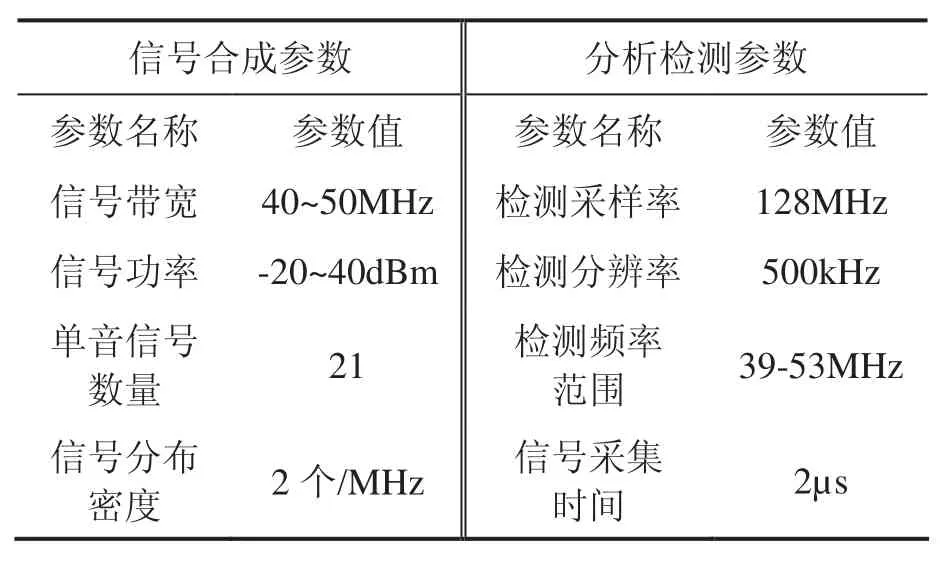
表1 信号模拟合成与功率检测参数

图4是2种检测算法的结果对比：（1）2种检测算法对应的折线都无法与“*”点表示的实际功率完全重合，说明2种检测方法都存在一定的检测误差；（2）在21个存在信号的待测频点，实折线与“*”点的重合度明显好于虚线，说明实线对应的检测算法其检测误差要远远小于传统的频域周期图能量检测方法；（3）在8个实际不存在信号的待测频点，虚线对应的检测结果远远大于实线，说明虚线对应的频域周期图能量检测方法在检测过程中信号泄露更严重，易导致无信号频点产生虚警检测结果.综上所述，本文所述快速时域检测方法在所有检测频点中其检测误差均优于传统频域检测方法，说明该方法在计算效率提升的同时保留了时域检测误差小的优点，与计算规模相似的频域检测方法相比具有更优越的检测性能.

3.2 仿真实验二

仿真实验一可以直接观察2种能量检测方法的性能对比，但也存在以下不足：（1）性能对比只有定性的观察对比，没有精确的定量分析；（2）尽管2种检测方法的算法复杂度属于同一等级O(MlogM)，但两者的实际计算成本并不完全一致，尤其受信号采集时间这一因素影响较大.仿真实验二在实验一的基础上更全面的比较上述2种能量检测方法的性能，具体改变如下：

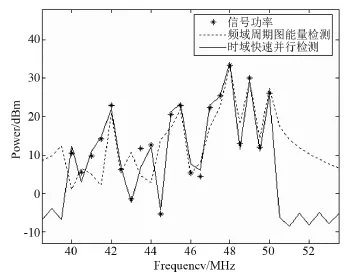
图4 能量检测方法的性能对比

2）以检测过程中乘法运算的数量衡量检测算法的计算成本.检测过程主要由乘法和加法运算构成，不管是硬件还是软件实现，乘法都远比加法运算复杂，为便于比较，以乘法运算数量表征计算成本.

3）基本沿用实验一的信号合成与分析检测参数，但根据信号采集时间的不同分别比较上述2种检测算法的检测误差和计算成本（见表2）.信号采集时间即信号截断时间，和算法检测性能直接相关，不同采集时间的对比，能体现检测算法在不同应用背景下（即检测性能要求不同）的性能和成本.表2显示：（1）不管信号采集时间是多少，快速时域能量检测方法的平均检测误差都明显小于频域能量检测方法，此结果再次验证了实验一的结论；（2）计算成本的对比显示，在相同信号采集时间条件下对比频域能量检测具有一定的优势，但在相同检测误差条件下对比，快速时域能量检测则具备明显的优势.例如信号采集时间为8µs时，频域检测方法的平均检测误差是2.58dB，不如快速时域检测方法在采集时间为1µs时的检测误差2.48dB，而此时快速时域方法对应的乘法数量为9216，远远小于频域检测方法对应的乘法数量49152.由此可见，在不同的应用背景下，只要检测误差的需求确定，快速时域检测方法在计算成本上与频域检测方法相比也具有明显的优势.

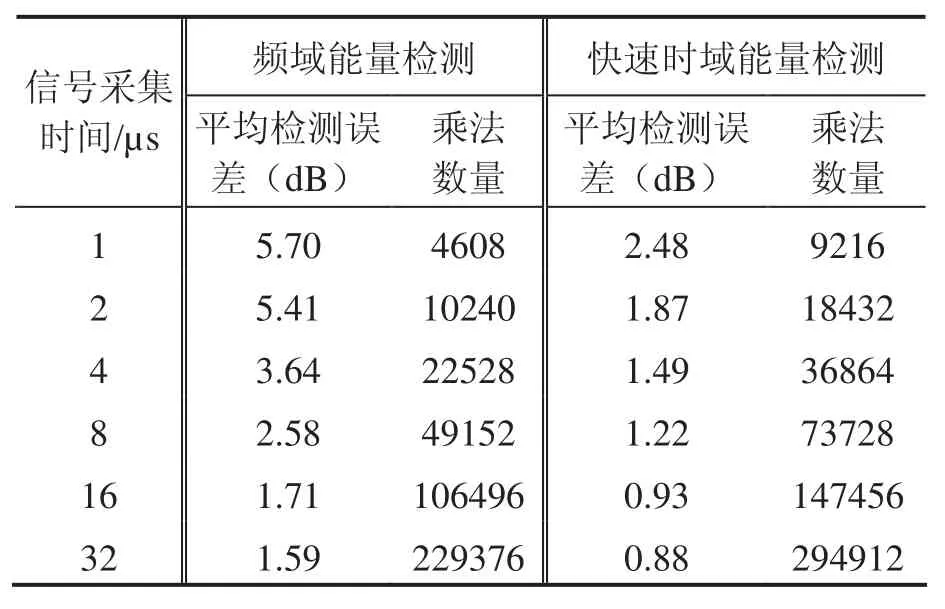
表2 两种能量检测方法的检测性能、计算成本对比

4 结 论

与传统的时域能量检测方法相比，本文所述的快速时域能量检测方法明显降低了算法复杂度，可实现大规模高分辨率的并行检测；与周期图等频域检测方法相比，由于受信号截断的影响较小，有效控制旁瓣，具有检测误差小的优点.通过检测精度与计算成本的比较，证明本文提出的快速检测方法在计算成本和检测性能上均优于频域能量检测方法，是一种适用于认知无线电系统的高精度高分辨率检测的并行时域能量检测方法.

[1] CABRIC D, MISHR A S and BRODERSEN R. Implementation issues in spectrum sensing for cognitive radios[C]//Asilomar Conference on Signals, Systems, and Computers, 2004：772-776.

[2] URKOWITZ H. Energy detection of unknown deterministic signals[C]//Proceedings of the IEEE, 1967，55： 523-531.

[3] WU J, LUO T and YUE G. An Energy Detection Algorithm Based on Double-Threshold in Cognitive Radio Systems[C]//Conference on Information Science and Engineering, 2009：493-496.

[4] YE J, ZHANG F and HU P. An energy detection scheme based on hysteresis-threshold for cognitive radio[C]// Conference on Communication Technology and Application, 2011：155-159.

[5] 马伟.认知无线电频谱检测技术研究[D].北京：北京邮电大学，2010.

[6] SHEN J, LIU S, WANG Y, et al. Robust energy detection in cognitive radio[J]. IET Communications, 2009，3： 1016-1023.

[7] JOSHI D R, POPERSCU D C and DOBRE O A. Adaptive spectrum sensing with noise variance estimation for dynamic cognitive radio systems[C]// Conference on Information Sciences and Systems, 2010： 1-5.

[8] YE Z, MEMIC G and GROSSPIETSCH J. Energy detection using estimated noise variance for spectrum sensing in cognitive radio networks [C]// Conference on Wireless Communications and Networking, 2008：711-716.

[9] XIN Y, ZHANG H and RANGARAJAN S. A simple sequential spectrum sensing scheme for cognitiveradio[C]//Conference on Global Telecommunications, 2009：1-6.

[10] KUNDARGI N and TEWFIK A. A performance study of novel sequential energy detection methods for spectrum sensing[C]//Conference on Acoustics Speech and Signal Processing, 2010：3090-3093.

[11] JI X, ZHANG S and GAO Y. Performance Analysis of Energy Detection for Cognitive Radio in Fading Channels[J]. Telecommunication Engineering, 2010，2： 26-32.

深圳职业技术学院国际武术交流中心十周年庆典隆重举行

2015年12月12日，我校国际武术交流中心成立十周年庆典，暨中国武术文化发展论坛和第九届深圳武术公开赛在西丽湖校区体育馆隆重举行。国际影星李连杰、甄子丹的授业恩师、中国武术九段、原中国武术协会副主席吴彬，学校党委书记、校长刘洪一，深圳市文体旅游局巡视员、深圳市体育总会副会长柯刚明等参加了庆典仪式。醒狮表演、铁砂掌、跆拳道等一系列精彩绝伦的表演让所有来宾和观众拍手叫好，将中国竞技武术的精髓展现得淋漓尽致。十年来，中心与国外多所著名大学及港澳台等武术机构建立了友好合作关系，搭建了一个具有国际水平的武术推广与交流平台。同时，在培养师生运动养生兴趣，增强运动意识，提高文化综合素质和传承发扬中华民族宝贵文化遗产等方面发挥了重要作用.

（深职院 宣传部）

A Fast Algorithm of Time-domain Energy Detection for Cognitive Radio

HE Jianbiao

（School of Electronic and Communication Engineering, Shenzhen Polytechnic, Shenzhen, Guangdong 518055, China）

Energy detection is the most common sensing method for cognitive radio. A fast algorithm for time-domain detection is presented in this paper. Parallel detection model, which consists of down-convertors and low-pass filters, is adopted in this algorithm. Fast calculation of this model is achieved by sharing the low-pass multi-band filters and applying IFFT module instead of down-converts. Simulations demonstrate that the purposed algorithm can give more excellent performance, including error detection and cost calculation, in comparison with traditional time-domain and frequency-domain detection methods.

cognitive radio; spectrum-sensing; time-domain energy detection; fast algorithm

TN911.23

A

1672-0318（2016）01-0003-06

10.13899/j.cnki.szptxb.2016.01.001

2015-09-09

*项目来源：“深圳市公共文化数字工程实验室（深圳市重点实验室）”、“南山区移动互联技术公共服务平台”资助项目

何健标（1981-），男，广东五华人，工程师，博士，研究领域为通信与信息系统以及数字信号处理.