函数视角下的数列问题探究

◇　山东　王　涛

(作者单位：山东省寿光一中)



函数视角下的数列问题探究

◇山东王涛

数列作为一种特殊的函数,其中蕴含着函数的本质及意义,具有函数的一些固有特征．因此我们在解决数列问题时,应充分利用函数有关知识,以函数的概念、图象、性质为纽带,架起函数与数列间的桥梁,揭示它们间的内在联系,从而有效地“化解”数列问题．本文对函数视角下的数列问题进行探究．

1　周期函数视角下的数列问题

A若a3=4,则m可以取3个不同的数;

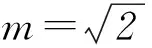
C存在m∈Q,且m≥2,数列{an}是周期数列;

D对任意T∈N*且T≥2,存在m>1,使得{an}是周期为T的数列.

2　导数与函数性质背景下的数列问题

Aa=1;

B 当n∈N*时,yn的最小值为5/4;

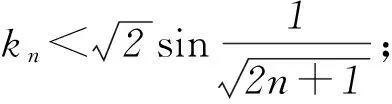
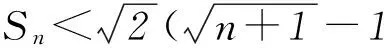
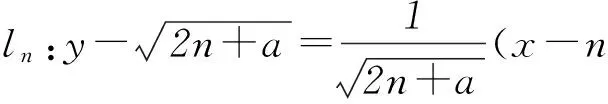
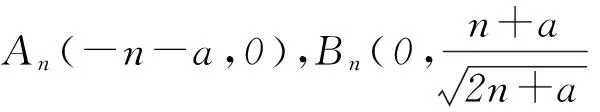
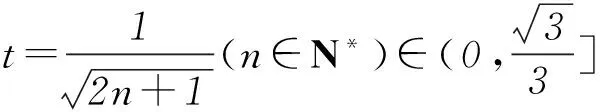
对于D，Sn=k1+k2+…+kn=

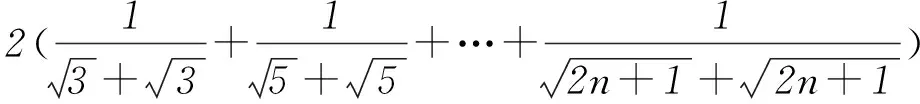
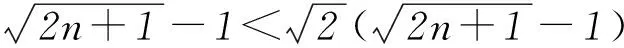
正确．

3　三角函数视角下的数列问题

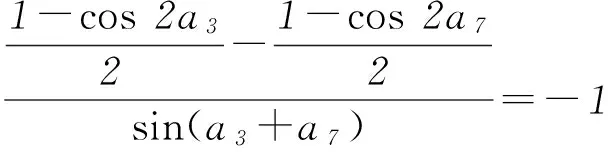
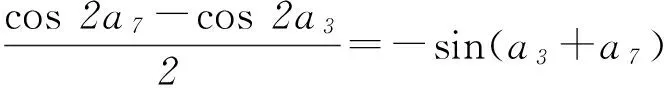
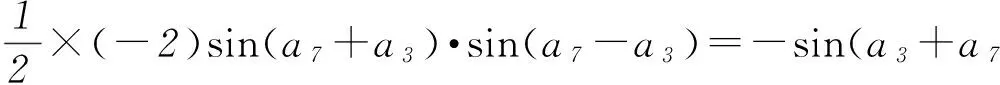
因为sin(a3+a7)≠0,所以sin(a7-a3)=1,4d=2kπ+π/2∈(0,4)，所以k=0, 4d=π/2,d=π/8.

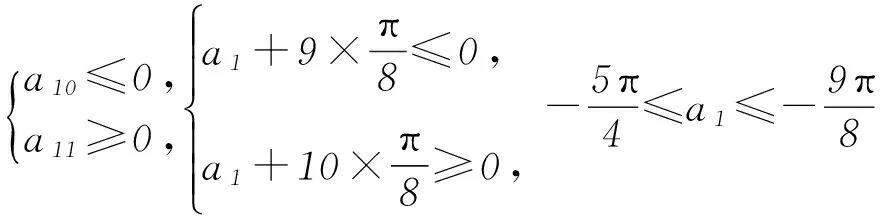
数列作为一种特殊的函数，具有函数的一些固有特征，函数的周期性、单调性、数形结合等在解数列问题中起到了举足轻重的作用.用函数思想解数列问题时，不仅要用到函数的形式，更重要的是运用函数的思想方法．

(作者单位：山东省寿光一中)