几道多变量问题的解题策略分析

◇　北京　　张留杰　陶　军　童嘉森(特级教师)

(作者单位：1.北京市陈经纶中学 2.北京市怀柔区第一中学 3.北京市第八十中学



几道多变量问题的解题策略分析

◇北京张留杰1陶军2童嘉森3(特级教师)

函数性质的综合应用是历年高考的热点之一,以函数为背景的双变量或多变量问题在高考模拟考试中层出不穷,并且大多与不等式及最值综合在一起.下面就结合几道试题谈谈这类问题的解题策略和逐步转化问题的方法.

(1)f(x)=2x时,H(0)=________;

(2)f(x)=x2且t∈[1,2]时,函数H(t)的值域为________.

(1) 当t=0时,f(t)=f(0)=0,可得|2x|≤2,即x∈[-1,1],所以对任意的x∈[-a,b]都有x∈[-1,1],所以a+b的最大值为2, 即H(0)=2.

(2) 方法1不等式|f(x)-f(t)|≤2可化为|x2-t2|≤2,所以t2-2≤x2≤t2+2. 因为t∈[1,2],所以只需分t2-2≤0和t2-2>0这2种情况求解x的范围.

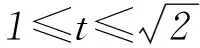
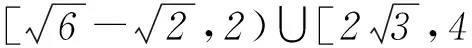
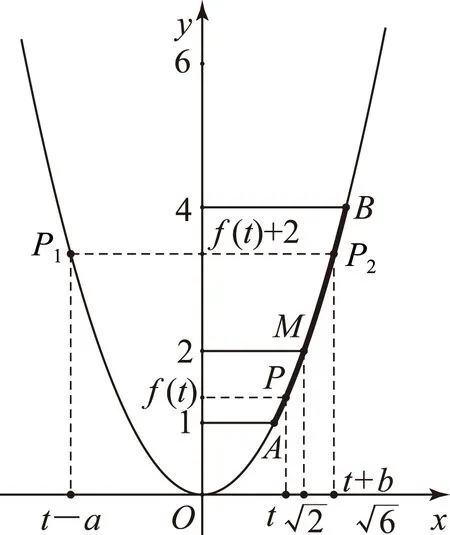
图1

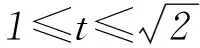
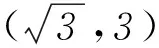
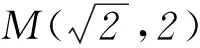
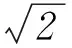
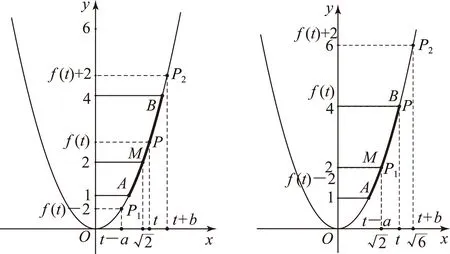
图2　　　　　　　　　　　　图3

设集合M={(m,f(n))|m,n∈[a-1,a+1]},若M中的所有点围成的平面区域面积为S,则S的最小值为________.

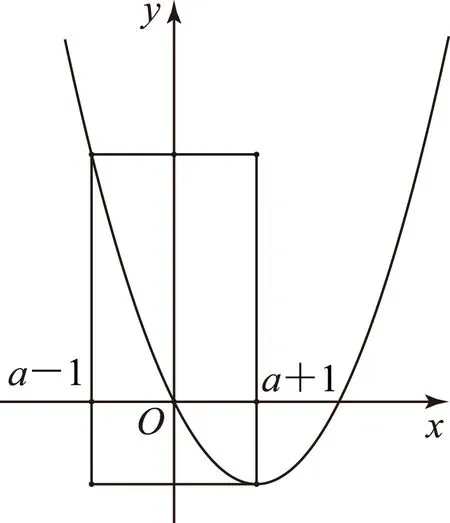
图4

如图4,集合M构成的平面区域为矩形,其宽为|(a-1)-(a+1)|=2,函数f(x)=x2-2x的对称轴为x=1.

1) 当a+1<1,即a<0时,矩形长为|f(a+1)-f(a-1)|=|(a+1)2-2(a+1)-[(a-1)2-2(a-1)]|=|(a+1)2-(a-1)2+2[(a-1)-(a+1)]|=|4a-4|=4|a-1|.所以矩形面积S=8|a-1|,无最小值.

2) 当a-1>1,即a>2时,矩形长为|f(a+1)-f(a-1)|=4|a-1|,面积为S=8|a-1|,无最小值.

3)a+1≥1且a-1≤1,即0≤a≤2时,若0≤a<1, 其长为|f(a-1)-f(1)|=(a-2)2,面积S=2(a-2)2,无最小值;若1≤a≤2,其长为|f(a+1)-f(1)|=a2,面积S=2a2,此时a=1，S有最小值2.

综上,平面区域的面积S的最小值为2.

(1) 函数h(t)的最大值是________;

(2) 函数h(t)的单调递增区间为________.

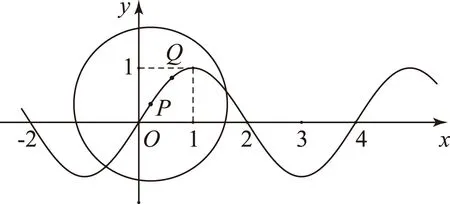
图5

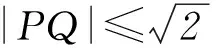
(作者单位：1.北京市陈经纶中学 2.北京市怀柔区第一中学 3.北京市第八十中学