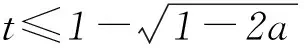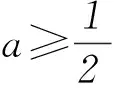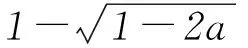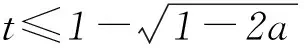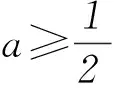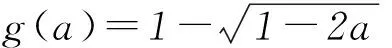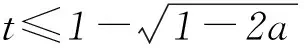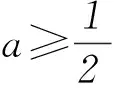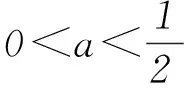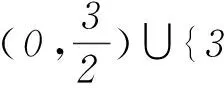一道高三函数模拟题的启示

◇　天津　明廷军

(作者单位：天津市耀华中学)



一道高三函数模拟题的启示

◇天津明廷军

对于涉及自变量取值范围的二次函数值域问题,我们常见的思路是将自变量的取值范围与抛物线的对称轴位置进行分析讨论,本题通过对这一传统方法的研究,提出一种新的研究思路和技巧．

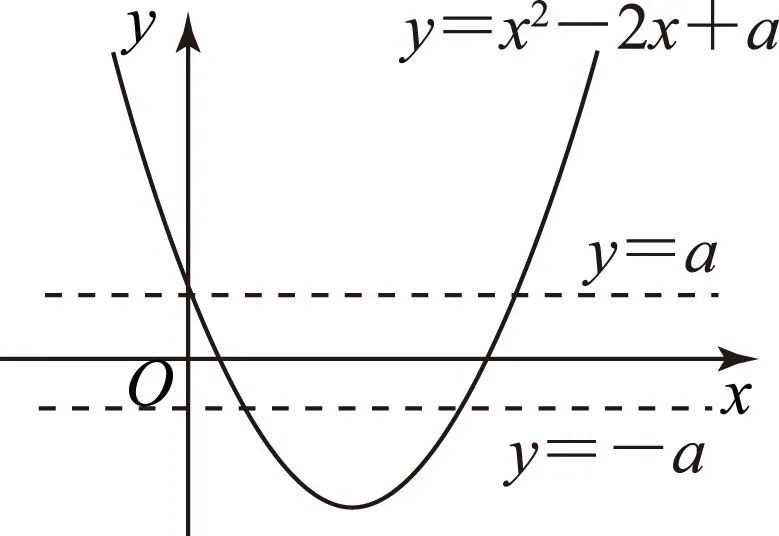
方法1因为f(x)=x2-2x+a，所以函数f(x)的图象开口向上,对称轴为x=1.

1) 当0

fmax(x)=f(0)=a,

fmin(x)=f(t)=t2-2t+a.

2) 当t>1时,f(x)在[0,1]上为减函数,在[1,t]上为增函数,则

fmax(x)=max{f(0),f(t)}=

max{a,t2-2t+a}≤a,

fmin(x)=f(1)=a-1≥-a.

方法2因为f(x)=x2-2x+a，所以函数f(x)的图象开口向上,对称轴为x=1.

1) 当0

fmax(x)=f(0)=a,

fmin(x)=f(t)=t2-2t+a.

2) 当t≥1时,f(x)在[0,1]上为减函数,在[1,t]上为增函数,则

fmax(x)=max{f(0),f(t)}=

max{a,t2-2t+a}≤a,

fmin(x)=f(1)=a-1≥-a.

方法3因为f(x)=x2-2x+a，所以函数f(x)的图象开口向上,对称轴为x=1.

1) 当0

fmax(x)=f(0)=a,

fmin(x)=f(t)=t2-2t+a.

2) 当t=1时,f(x)在[0,t]上为减函数,所以

fmax(x)=f(0)=a,

fmin(x)=f(1)=a-1．

此时f(2)=f(0)=a,即1≤t≤2时均满足条件，所以tmax=2,即g(a)=2,但这与t=1矛盾,故舍去．

3) 当t>1时,f(x)在[0,1]上为减函数,在[1,t]上为增函数,则

fmax(x)=max{f(0),f(t)}=

max{a,t2-2t+a}≤a,

fmin(x)=f(1)=a-1≥-a.

解题时对于这种临界状态,我们应该怎么去把握更好呢?如果能撇开对参数t的讨论,将tmax看成a的函数(受题目“记t的最大值为g(a)”的启发),通过定义域去求函数的最大值就会方便和直观很多,大大降低了错误的可能性!

方法4令f(x)=-a,即x2-2x+a=-a,亦即x2-2x+2a=0，其中Δ=4-8a.

图3

综上可知,

所以g(a)的值域为(0,1)∪{2}．

请同学们利用方法4解答下面的练习.

练习已知a、t为正实数，函数f(x)=x2-3x+a,对任意x∈[0,t],都有f(x)∈[-a,a],对每一个正实数a，记t的最大值为g(a)，则g(a)的值域为________.

(作者单位：天津市耀华中学)