大跨度拱桥主拱肋风载系数的大涡模拟*
2016-11-14应旭永许福友
应旭永 许福友 张 哲
(大连理工大学桥梁工程研究所 大连 116023)
大跨度拱桥主拱肋风载系数的大涡模拟*
应旭永 许福友 张 哲
(大连理工大学桥梁工程研究所 大连 116023)
以某设计中的大跨度拱桥为工程背景,基于ANSYS FLUENT 软件平台对该桥双拱肋精确建模,采用三维大涡模拟方法详细研究了主拱肋的风载系数及其绕流场.计算所得主拱肋不同位置的风载系数是进行结构风载内力计算及随机风振分析的基础.结果表明,上游拱肋的阻力系数略小于单拱肋绕流的数值,下游拱肋主要受负阻力作用;下游拱肋的风载系数脉动值明显大于上游拱肋的数值.上游拱肋的迎风面受正压作用,其他表面主要受负压作用,下游拱肋表面相比上游塔柱表面具有更大的脉动风压.同时给出了拱肋周围的速度等值线图、迹线图和流线图,并通过流场图进一步对计算结果进行了机理解释.
拱肋;风载系数;大涡模拟;计算流体力学;流场
0 引 言
现代大跨度拱桥的跨径日益增大,使得结构的阻尼和刚度大幅度降低,导致结构对风的作用更加敏感,因此桥梁结构的风振稳定性成为大跨度拱桥安全的控制因素之一.在主梁尚未架设前,缺少吊杆主梁体系的约束,拱肋处于刚度较低阻尼较小的自立状态,是拱桥施工过程中最不利的状态[1]和通常风洞气弹模型实验所给出的风致振动位移相比,给出拱肋各截面的风载系数更便于指导其结构设计.此外主拱的前后两拱肋间存在遮挡效应,使得其周围流场变得非常的复杂,试图通过相关行业规范或经验来确定主拱肋不同位置的风载系数将变得不可能[2].因此如何确定主拱圈不同位置的风载系数,是大跨度拱桥设计中需要考虑的关键问题.郑史雄等[3-5]采用测力风洞实验或数值模拟研究了主拱单拱和双拱节段模型的风载系数,结果表明,上、下游的拱肋的风载系数有较大的差异,且随着两拱肋的间距宽度和攻角变化.楼小峰等[6]采用二维数值模拟方法,计算了钢管混凝土拱桥哑铃型拱肋的风载系数.实际上对于大跨度拱桥,两拱肋的间距宽度是随着跨径方向变化的,且主拱肋及横梁之间存在强烈的气流干扰现象,因此需要根据实际结构设计,建立三维模型才能更准确的模拟拱肋的绕流场和风载系数.
文中以某设计中的拱桥为工程背景,详细研究了主拱肋的风载系数及其绕流场.该桥为一座系杆拱-T型刚构协作体系桥[7],主跨为500 m,主拱肋为矩形截面,两拱肋中间设置14道横梁,见图1.基于ANSYS FLUENT 软件平台对该桥主拱肋精确建模,利用大涡模拟对模型表面平均风压和风荷载进行了数值模拟,同时计算得到主拱肋不同位置的风载系数,最后对拱肋周围风场特性进行了较详细的分析.
1 数值计算方法
1.1 湍流模型的选取
大量研究表明,由于钝体绕流会产生分离、再附、冲撞、环绕、涡等一系列复杂的流动结构,湍流模型的选取对计算结果起主要作用.由Stathopoulos等[8-9]所提出的大涡模拟(LES)理论近年来发展迅速,已被列为湍流的高级数值模拟范畴.文中将采用大涡模拟进行CFD数值模拟计算.大涡模拟的控制方程为结合Smagorinsky亚格子尺度模型的Navier-Stokes方程.
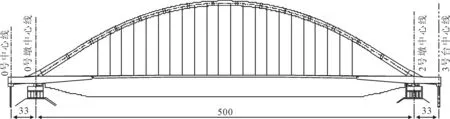
图1 全桥构造简图(单位:m)
(1)

1.2 计算模型及网格划分
数值计算模型按1∶100缩尺比并严格按照工程设计方案的比例尺寸建立3D几何实体模型.依次把两根拱肋沿着横桥向(风向)分为上游、下游拱肋,每根拱肋沿着纵桥向又分为30个分块,具体分块形式及坐标体系见图2.

图2 主拱肋三维模型及结构分块
计算域为一直径20m,高1.5m的圆柱形区域,拱肋模型放置在计算域的中心位置,阻塞率满足数值模拟中一般认定的小于3%的原则.由于模型的拱肋和横梁具有较复杂的外形,结构比较复杂,因此在划分计算网格时候对计算域进行了分块处理:在原计算域中心模型附近分割一个长方体内域(长×宽×高为6.4m×2m×1.5m),使用加密的四面体非结构化网格进行离散;内域和原流域的边界面之间称为外域,由于这部分形状比较规则,采用六面体结构化网格进行离散.计算域的总网格数为450万左右,计算域整体网格布置和模型底部局部网格见图3.

图3 网格示意图
1.3 边界条件及求解策略
计算域入口处采用速度入口边界条件,来流风速为U=5m/s;出流面采用完全发展的出流边界条件,保证各个物理量沿流向不再变化;流域顶部采用自由边界;取流域底部所在的地平面为壁面无滑移边界条件;结构表面采用无滑移的壁面条件.数值计算采用3D分离式求解器,压力与速度耦合采用SIMPLEC算法.时间项离散采用二阶迎风格式,对流项采用数值耗散低的二阶中心差分格式进行离散,计算时间步长取0.001s.
2 结果分析与比较
2.1 不同位置拱肋的风载系数
在数据分析中,为了便于数据的比较和计算,对各个力分量做量纲一的量化处理,并定义拱肋各个分块的风载系数:
(3)
(4)
式中:ρ为空气密度;U为风速;FDi为第i分块横桥向所受的气动力,即气动阻力;FLi为第i分块竖向所受的气动力,即气动升力;Sxi为第i分块横桥向投影面积,Syi为第i分块竖向投影面积;CDi和CLi分别为阻力系数和升力系数(其他方向分量或较小,或与所研究的拱肋最不利受力状态无关,故略之).

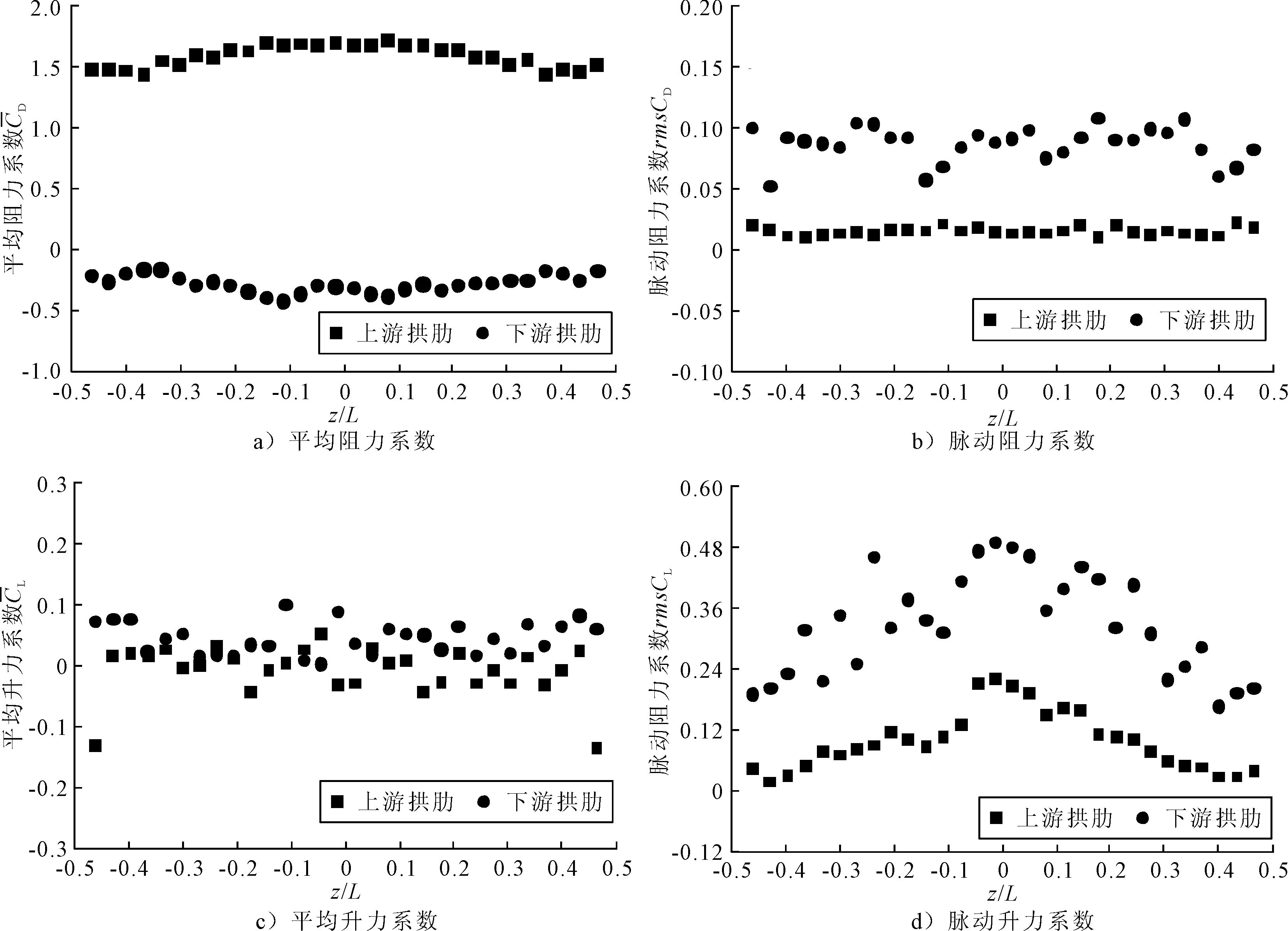
图4 主拱肋各结构分块截面风载系数
上游拱肋的脉动阻力系数rms CD数值较小;而下游拱肋的rms CD相对较大,数值基本保持在0.1左右;上游、下游拱肋的rms CD数值沿着纵桥向基本保持不变.相比阻力系数,拱肋的升力系数具有更明显的脉动特性,尤其是下游拱肋,因此脉动升力系数rms CL数值也相对较大.此外,rms CL沿着纵桥向从拱脚到跨中,数值逐渐增大,并在跨中位置达到最大值.
空气绕拱肋流动时不断的产生漩涡并发生流动的分离.生成的漩涡由拱肋表面周期性交替脱落,向下游运动,从而对桥塔产生周期变化的作用力——涡激力.
实际拱肋为一个振动体系,当漩涡脱落频率与结构自振频率相当时,将可能引起共振,危害极大.对于涡激共振,在拱肋自立状态下几乎是不可避免的.为了更加清晰的了解拱肋的受力情况,通过FFT计算了拱肋跨中位置截面风载系数的幅值谱,见图5~6.从幅值谱曲线可以看出,拱肋的阻力系数和升力系数都有个明显的占优主频,阻力系数主频为8.557Hz,升力系数主频为4.278Hz,阻力系数主频是升力系数主频的2倍,这与理论相符.上游、下游拱肋风载系数的主频数值是一致的.此外可以观察看到一些低频和高频信号,这个信号在阻力系数的幅值谱中更加强烈,引起这一低频信号的主要原因是流场的三维湍流特性.
2.2 平均风压系数分布
数值模拟的拱肋模型表面的测点i压力数据将由下面公式计算得到风压系数.
(5)

图5 跨中位置拱肋阻力系数时程曲线及幅值谱
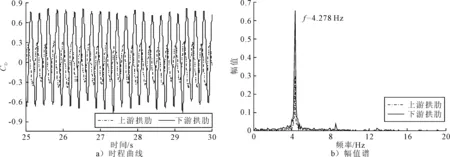
图6 跨中位置拱肋升力系数时程曲线及幅值谱
式中:Cpi为桥塔表面测点i的风压系数;pi为测点i的风压值;p∞,U∞为参考点的静压和风速,选取入口处为参考点;N为样本长度.
图7a)为拱肋模型迎风面和背风面的平均风压系数分布.可见上游拱肋迎风面基本承受正风压.两拱肋上下表面的风压基本为负值,在上游拱肋迎风面和上、下表面的夹角处,风压从正值突变为较大的负值,风压系数达到-1.4左右,这是由于流动在该夹角处产生了大分离引起的.在下游拱肋迎风面上,由于处于上游拱肋的尾流区,使得出现了较大的负压区.沿纵桥向从跨中到拱脚处,随着两拱肋的间距逐渐增大,上游拱肋上下表面、背风面及下游拱肋迎风面的负压值逐渐减小,其他面的风压变化梯度较小.图7b)为拱肋模型迎风侧和背风侧的表面脉动风压系数分布.相比上游拱肋,下游拱肋的脉动风压系数较高.

图7 拱肋表面压力系数分布云图
2.3 拱肋周围风场分析

图8 拱肋不同位置的速度等值线剖面图
图8为拱肋模型不同位置的速度等值线剖面图.可见不同位置处,在拱肋尾流处均发生了不同形式的周期性漩涡脱落.在拱脚处,由于拱肋的周围流场受到海平面的干扰较强,其尾流涡脱受到一定程度上的抑制,所以导致图4和图7所示的rms CL和脉动风压系数沿着纵桥向从跨中到拱脚,数值逐渐减小.图9为大涡模拟捕捉到的跨中位置拱肋的迹线图,分离、再附、冲撞、环绕、涡等钝体绕流现象均得到了准确的反映;在上游拱肋的上下表面前沿处出现了气流分离,这些地方正是前文所提到出现高负压的区域;在两塔柱中间卷起了各种尺度的漩涡相互作用,形成复杂的干扰流场.

图9 跨中位置拱肋的迹线图
对于风载系数和风压系数脉动值下游拱肋明显大于上游拱肋,原因主要为:(1)下游拱肋位于从上游拱肋分离的脉动高速区;(2)从上游拱肋脱落的涡直接打在下游塔柱上,在下游塔柱的前角产生额外的角动量,从而在下游拱肋上产生较强的脉动力;(3)从上游拱肋脱落的涡通过对流过程转变成小尺度的涡,这增加了对下游拱肋而言的来流的脉动性.这也说明了下游拱肋表面相比上游拱肋表面具有更大的脉动风压.
图10为不同时刻拱肋跨中截面流线图,在上游拱肋迎风面分离的流线会间歇性的再附到下游拱肋的上下表面.在t=32.11s时刻,在两拱肋中间形成了一个大尺度漩涡A,其漩涡中心在两拱肋间隙中心偏上位置;在这个漩涡A的下方还生成了一个与其反向旋转的漩涡B.在t=32.15s和t=32.19s时刻,漩涡A的尺度不断减小,漩涡B的尺度不断增大,但其漩涡中心的位置基本保持不变.在t=32.23s和t=32.27s时刻,漩涡A向上游移动;而漩涡B向下游移动,尺度也逐渐减小直到从下游拱肋下表面脱落.在t=32.23s时刻,漩涡A的尺度逐渐增大并迁移回原来位置.由于漩涡A的作用,致使下游拱肋迎风面受到较大的负压作用,从到导致下游拱肋产生负的阻力系数.

图10 不同时刻拱肋跨中截面流线图
下游拱肋的尾流呈现出典型的卡门涡街现象.首先在下游拱肋背风面上侧产生了1个顺时针旋转的漩涡C;随着时间的推移,漩涡C尺度逐渐增大,漩涡中心不断向下游迁移,最终从拱肋表面脱落.然后在下游拱肋背风面下侧又产生了另1个逆时针旋转的漩涡D;漩涡D同样也会随着时间的推移从拱肋表面脱落.可见在1个升力变化周期内,两拱肋中间完成了1个漩涡的生成和脱落,而下游拱肋尾流完成了2个漩涡的生成和脱落.这是由于受到海平面和周围拱肋断面的干扰作用,不同位置拱肋的绕流场在1个周期内都呈现出上下不对称变化.
3 结 论
1) 根据数值模拟计算得到的拱肋不同位置的风载系数是进行结构各截面风载内力计算及整体结构随机风振分析的基础.上游拱肋的阻力系数略小于单拱肋绕流的数值,下游拱肋主要受负阻力作用;但是对于风载系数脉动值下游拱肋明显大于上游拱肋.基于风载时程曲线的频谱分析可知阻力主频是升力主频的两倍,上游、下游拱肋风载的主频数值是一致的.
2) 上游拱肋的迎风面主要受正压作用,其他表面主要受负压作用,迎风面拐角区域有高负压、高风压梯度的出现.下游拱肋表面相比上游塔柱表面具有更大的脉动风压.
3) 文中的数值模拟同时给出了拱肋周围的速度等值线图、迹线图和流线图,较准确地预测了分离、再附、冲撞、环绕、涡等钝体绕流现象,并通过流场图对计算结果进行了机理解释.
[1]程进,江见鲸,肖汝诚,等.静风荷载作用下大跨度钢拱桥施工稳定性的参数研究[J].计算力学学报,2004,21(1):50-55.
[2]中交公路规划设计院.公路桥梁抗风设计规范:JTG/T D60—01—2004[S].北京:标准出版社,2004.
[3]郑史雄,唐煜.大跨度拱桥矩形拱肋静风阻力研究[J].桥梁建设,2014,44(5):33-38.
[4]晏致涛,李正良.中承式拱桥主拱静风载试验及数值模拟[J].重庆大学学报,2008,31(9):1059-1063.
[5]于洪刚,曲松,赵林.矩形拱肋定常气动力系数识别研究[J].湖南交通科技,2009,35(4):87-90.
[6]楼小峰,曹丰产,林志兴.串列钝体绕流的数值计算[J].同济大学学报(自然科学版),2002,30(5):604-608.
[7]张哲,朱伟志,李文武,等.系杆拱-T型刚构协作体系桥:CN202347427 U[P].2012-07-25.
[8]STATHOPOULOS T. Computational wind engineering: past achievements and future challenges[J]. Journal of Wind Engineering & Industrial Aerodynamics,1997,67:509-532.
[9]是勋刚.湍流[M].天津:天津大学出版社,1994.
Large Eddy Simulation on Aerostatic Coefficients of Main Arch Ribs of Long-span Arch Bridge
YING Xuyong XU Fuyou ZHANG Zhe
(InstituteofBridgeEngineering,DalianUniversityofTechnology,Dalian116023,China)
Taking a long-span arch bridge as an engineering example, the aerostatic coefficients and flow field of main arch ribs are investigated in detail using the three-dimensional LES method. The double arch ribs are accurately modeled based on ANSYS FLUENT software platform. The numerically calculated aerostatic coefficients at different position of arch ribs are the foundation for the internal force calculation and random wind-induced vibration analysis of the structure. The results show that the drag coefficients of upstream arch rib are slightly smaller than the value for single arch rib. The downstream arch rib is mainly controlled by the negative drag force. The fluctuation values of aerostatic coefficients of downstream arch rib are larger than that of upstream arch rib. The windward side of upstream arch rib is suffered from positive pressure, while the other surfaces of arch ribs are mainly suffered from negative pressure. Comparing with the downstream arch rib, the surface wind pressure of upstream arch rib has much higher fluctuating values. The velocity contour, pathlines and streamlines around the arch ribs are also presented. Through the analysis of flow chart, the mechanism for the calculated results is further explained.
arch rib; aerostatic coefficient; large eddy simulation; computational fluid dynamics; flow field
2016-08-26
*973国家重点基础研究发展计划项目(2015CB057705)、国家自然科学基金项目(51478087)资助
U445 doi:10.3963/j.issn.2095-3844.2016.05.010
应旭永(1987- ):男,博士生,主要研究领域为桥梁风工程
