无限弹簧振子链的脉冲波
2016-11-14邱为钢
邱为钢
(湖州师范学院理学院,浙江湖州 313000)
无限弹簧振子链的脉冲波
邱为钢
(湖州师范学院理学院,浙江湖州 313000)
给出了一维和两维无限长弹簧振子链的波动方程,这些方程可以看作数列的递推关系式,从而用产生函数法求解.一维解是偶数和奇数阶贝塞尔函数,对应于第一类和第二类脉冲波,分别取起始位移或速度离散奇异分布,两维解也是两种类型的脉冲波.文章还讨论了它们的级数展开式,渐近展开式,波形图及对称性.
弹簧振子;产生函数法;脉冲波
假设这样的物理模型:一个无限长弹簧振子链,每个物体(质点)质量相同,每个弹簧的弹性系数相等.给任意一点一个初始位移或者初始速度,其余点保持不动,随着时间推移,每个质点偏离平衡位置位移量随时间怎么变化,有无解析表达式?文献[1]发现,给任意一点一个初始扰动(位移)同时其余点保持不动,各点离开平衡位置的偏移量可以用偶数阶的贝塞尔函数表述,并把这种波形称为脉冲波.一个简单自然的推广是,奇数阶的贝塞尔函数描述什么样的波形?是否对应初始速度分布的脉冲波?笔者利用数学方法发现,这个猜测正确,并把这两种脉冲波推广到了两维无限弹簧振子链.
不管什么样的波形,它们满足的波动方程是一样的,不同的是初始条件和边界条件.先简要推导一维无限长弹簧振子链的波动方程,设弹簧链上质点质量为m,弹簧为理想弹簧,质量为零,弹性系数为.第n个质点偏离平衡位置的位移量为un(t),左右两边弹簧的胡克力分别是-k(un-un-1)和-k(un-un+1),由牛顿定律,得到
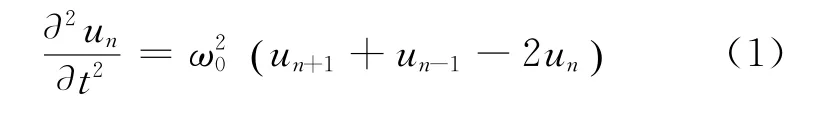
为讨论方便,令ω0=1.文献[1]给出的解是un(t)= J2n(2t),注意到贝塞尔函数有这样的产生函数式[2]

我们猜想un(t)=J2n+1(2t)也满足波动方程式(1).定义产生函数F±(t,z)为

它们满足以下微分方程

对比式(5)两边zn的系数,就得到满足波动方程式(1)的解为
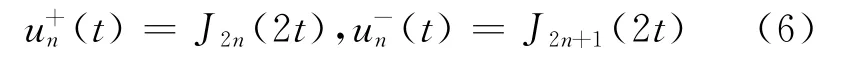
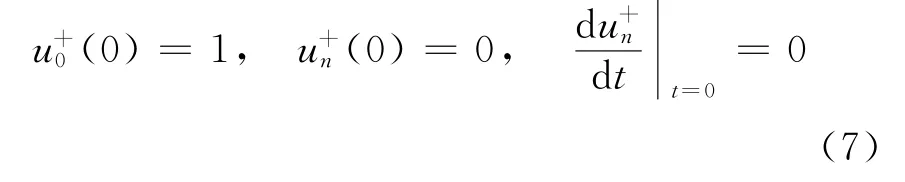
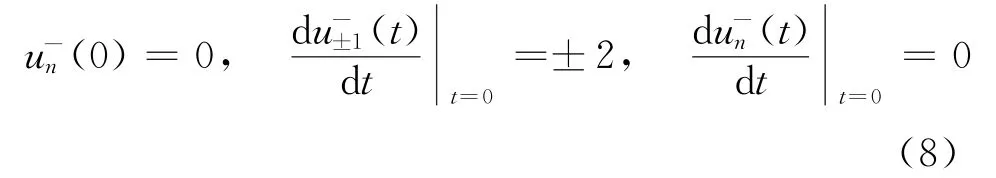
其次,我们考虑两维无限长弹簧振子链垂直链所在平面的运动模式,设第(m,n)个质点偏离平面的位移量为um,n(t),前后左右4个弹簧竖直方向胡克力分别是-k(um,n-um,n-1),-k(um,num,n+1),-k(um,n-um-1,n),-k(um,n-um+1,n),由牛顿定律,得到

继续用产生函数法求解式(9),为讨论方便,令ω0= 1,依照上文思路,设产生函数为
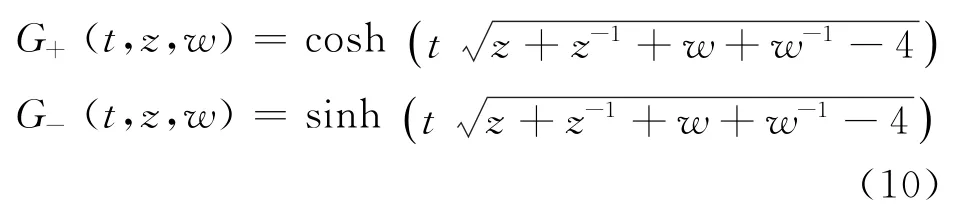
产生函数满足以下微分方程

产生函数有以下展开式

其中,

将式(12)代入式(11),对比zmwn的展开系数,就得到波动方程式(9).把式(10)代入式(12),展开t,得到
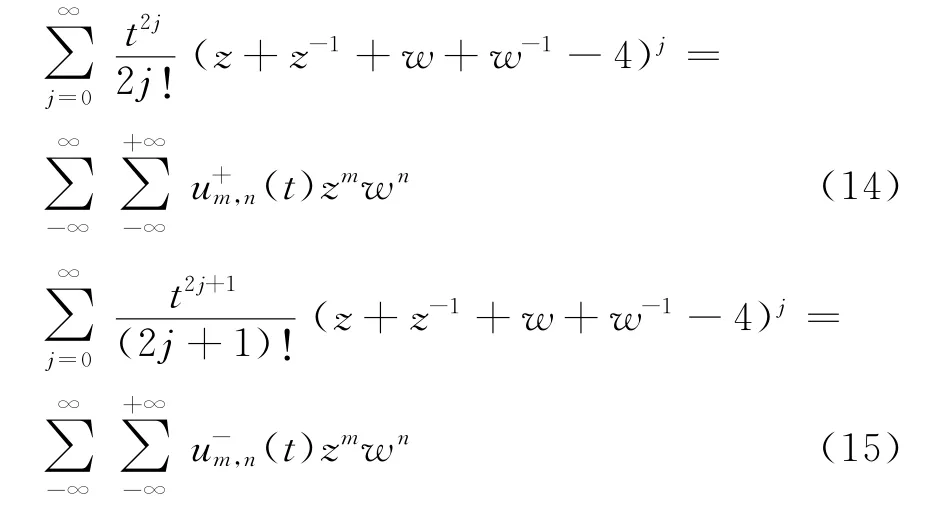
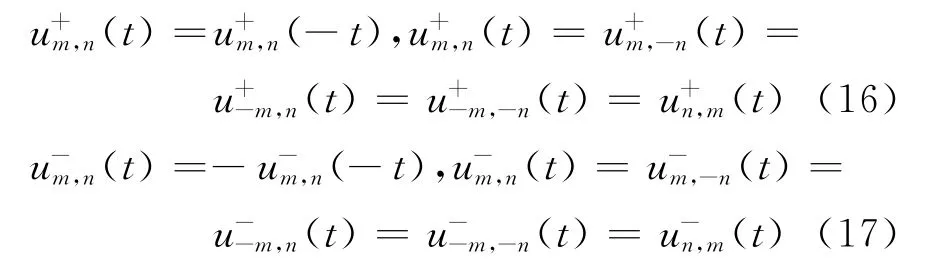



图1 不同时刻两维弹簧链中第一类脉冲波形图
由图1可以看出,随着时间推移,原点以外的各点开始振动,整个波动图形保持正方形对称性.


图2 不同时刻两维弹簧链中第二类脉冲波形图
由图2可以看出,随着时间推移,原点以外的各点开始振动,整个波动图形保持正方形对称性.
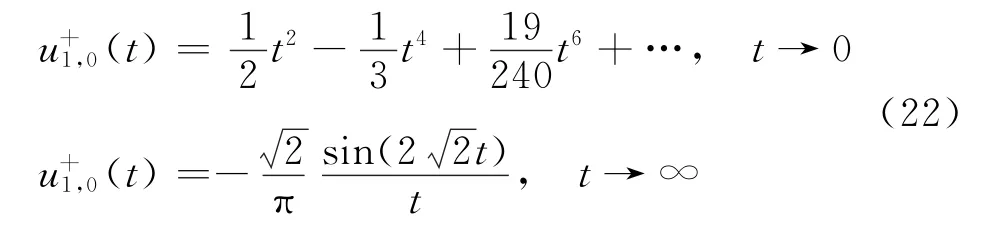

第一类脉冲波编号为(1,0)质点的振动图像由图3所示,其中实线由式(18)给出,虚线由式(22)给出.
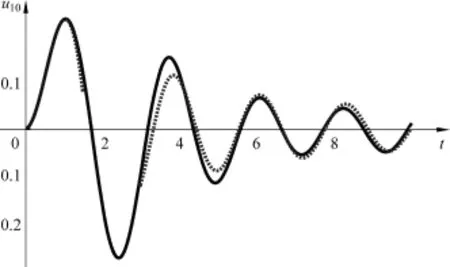
图3 第一类脉冲波编号为(1,0)质点的振动图像
第二类脉冲波编号为(1,0)质点的振动图像由图4所示,其中实线由式(19)给出,虚线由式(23)给出.
PULSE WAVE OF INFINITE SPRING OSCILLATOR CHAIN
Qiu Weigang
(School of Science,Huzhou Teachers College,Huzhou,Zhejiang 313000)
The wave equations of infinite spring oscillator chain are derived in one and two dimensions.These equations can be viewed as the recursive relation sequence,and can be solved by the generating function method.The one dimensional solutions are even order and odd order Bessel functions,corresponding to the first and the second pulse wave,respectively.The initial conditions are the discrete delta distributions of displacements or velocities,respectively.The two dimensional solutions are also two type of pulse wave.The series expansions,asymptotic expansions,configurations and symmetries of these pulse waves are discussed.
spring oscillator;generating function method;pulse wave
2014-12-05;
2016-06-04
湖州师范学院中青年教师卓越教学能力培养计划专题项目(2014ZYJH017);国家自然科学基金(11475062,11275067)资助.
邱为钢,男,副教授,主要从事数学物理和大学物理的教学研究.wgqiu@zihu.edu.cn
邱为钢.无限弹簧振子链的脉冲波[J].物理与工程,2016,26(4):62-64,68.
