中学物理教育应该强基础重通适
——一位大学教师的视角
2016-11-14陈奎孚
陈奎孚
(中国农业大学理学院,北京 100083)
中学物理教育应该强基础重通适
——一位大学教师的视角
陈奎孚
(中国农业大学理学院,北京 100083)
文章就一道力学题,给出了利用中学知识能够消化的一种解法.从笔者角度,谈论了教育应注重欣赏物理学的美,培养对物理的执着和热情,而不是记住几个特殊问题的解来应试.对相关文献中就该力学题的表述进行了分析.
教育;教学;物理;牛顿第二定律
叶玉琴老师于2011年发表了《对一道力学题的求解及感悟》一文(以下简称叶文),该文探究了一道求解技巧颇高的题目[1].原题如下:
题目 如图1所示,长为2L的轻质杆两端有质量为m的两个相同的小球A和B,A靠在竖直壁上,B与地板接触,两处均不计摩擦,开始时杆与水平面成θ0=60°,放手后A沿竖直墙壁向下,B沿地板向右从静止开始滑动.问:当θ为多大时A刚好脱离竖直壁?
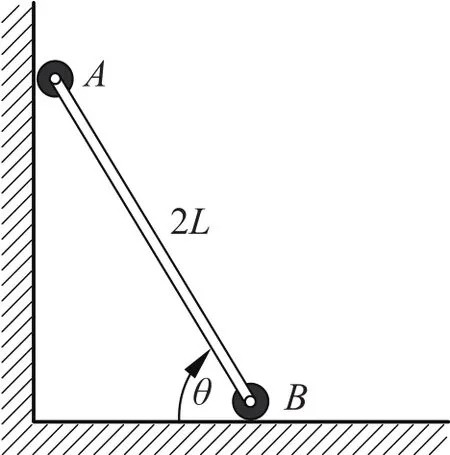
图 1
叶文给出了3个解析,解析一是从牛顿第二定律出发,这需要解微分方程,解析二是从动能定理出发,无需解微分方程(这是因为动能定理的导出过程已经完成了从微分到积分的运算),解析三则针对问题的特殊性分析出轻杆的拉力为零,再利用A绕B的瞬时向心加速度与A的重力关系得到答案.前两个解析需要的数学知识比较多,后一个解析只使用初等数学.
上文发表后,引起了众多教师的关注.肖光宏通过分析小球B动能极大值得到了答案[2].当然动能极大也意味着速度平方也极大,这是鲁良根方法[3].赵杰还介绍了Mathematica软件求极值方法[4].汪飞利用了A在脱离墙壁时刻的A和B加速度特殊性得到了答案[5].初毅等则提供了6种解析方法[6],并提出了自己一系列看法.由于本题在高中物理教学材料中频繁出现[1-26],其中若干话题仍有讨论和澄清的必要.理论力学教学中也有一道经典题目与此类似,即把A-B-轻杆换成均质杆[27,28].
1 解法
下面笔者先给出一个中学知识能够消化的解法.
由A-B-轻杆所组成系统的质心C位于AB中点,如图2所示.在A脱离竖直墙面之前不变,因此C轨迹为圆弧.设C的速度为vC,它沿圆弧的切向方向.vC与vA和vB的大小关系为
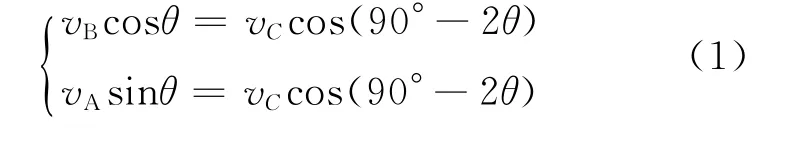
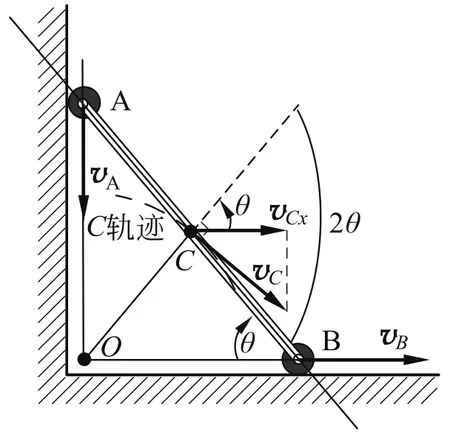
图 2

由机械能守恒可知该动能完全由A球重力势能V转换而来,因此

显然vC的大小随θ减小而增大,但是它的水平投影vCx需要乘上越来越小的sinθ.在两种因素的作用下,系统水平动量px开始从零增大,物理上这是因竖直墙壁向右支持力冲量的持续作用所造成的.当向右的支持力逐渐变化达到零时,px达到极大.此后,如果墙壁能够提供向左的拉力,那么px会再减小.由于墙壁不能够提供向左的拉力,A就脱离了墙面.所以在A脱离瞬间,px达到极大.为求极大的条件,将式(4)变为

显然2sin60°-2sinθ>0,sinθ>0,利用abc≤[(a+b+c)/3]3的不等式有

当(2sin60°-2sinθ)=sinθ时,上式“≤”中的等号成立,此时sinθ=3/3.这个条件在物理上也确实能够实现.
因此,当θ=sin-1(3/3)时A刚好脱离竖直壁.
2 讨论
下面谈一下笔者对本题和物理教育的一些感想.
卢潇还针对在中美贸易摩擦环境下美国LNG对中国的影响谈了自己的看法。他认为,总体来说,现阶段美国LNG对中国天然气供给影响不大,美国对中国的LNG出口量还比较小,在关税生效前,平均每月只有2船,主要以现货为主,2018年9-11月中国没有进口美国LNG。从成本端考虑,以12%斜率油价合同为基准,以当前10%的关税水平,在油价66美元/桶以上时,美国LNG具有竞争力;如果关税增加到25%,则平衡油价将达到76美元/桶,如果油价在70美元/桶波动,美国LNG存在竞争优势。但是,未来关税的不确定性和政治阻力会影响中国买家的选择,在这种背景下,中美贸易争端将有利于其他国家的LNG项目。
(1)即使采用上一节的方法,要求的技巧也很高.因而这类题目出现在高考模拟题中是否合适就是一个问题.笔者深信:大多数老师(当然包括笔者)解这个题目也要费一番周折.此题作为中学竞赛题尚可理解,但有必要拿这种题目来难为参加模拟考试的一般学生吗?特别是用极值法求解此题,难度在数学.优秀的物理教育者要通过让学生“享受”物理而对物理研究“上瘾”,进而将来对物理难题挑战,而不是在中学这个个性张扬,青春洋溢的季节用数学把未来的物理大师吓走.此题后来果真出现在30届(2013)全国中学生物理竞赛决赛考试试题上,但笔者深信,如果没有事先碰到过这个题目,让学生从头分析起,很难在短时间内完成.如果竞赛通过事前题海战术来背题,竞赛对学习物理的作用就打折了.
(2)接触与脱离问题在工程很常见,但是本题的条件太特殊.不管是笔者解法,还是前面提及的其它作者解法,都很难进行拓展.比如这里的mA=mB=m的限制.如果mA≠mB,质心的轨迹将会是椭圆.除了叶文的解析一和解析二能处理外(会很繁),其他作者(包括笔者的上一节方法)都应用不了.再比如,水平与竖直墙面的垂直的几何关系如果没有,也很难解出答案.
(3)适当习题训练是必要的,但是针对特殊问题的特殊解法在教育和教学中应该避免.我们不要让学生成天忙于求解特殊题型和记住对应的特殊解法.这些教学训练环节大量占用了学生对物理学美的享受,而且这些近乎残酷的训练在应试完毕后就几乎全忘了.
(4)将特定知识的适用范围拓广是科学发展的最重要动力,在教学中它应被更为强调.这样才能让学生在应试之后,保有对科学研究的兴趣和动力.今天会解多少怪题不重要,将来对研究有执着才重要.
(5)有些问题中学知识解决不了,或者就像本题,即使能解也很费劲,也难以推广.作为教师,应该鼓励学生定性地思考这些问题的影响因素,以及了解这类问题通用解法所需要的知识.鼓励他们将来大学阶段好好掌握高级的通用工具.随着计算机技术的发展,现在的数值软件和符号运算软件是未来的通用技术,应引导学生课余了解这方面的工具.
(6)物理教学不要玩文字游戏.比如图3(a)所示的圆盘受力分析,有些教师特别强调斜面没有弹力,认为图3(a)是错误的.其实大可不必说图3(a)是错误的.如果圆盘同斜面碰撞,斜面就可以有弹力.即使静止不动,通过平衡方程补充NB= 0也不是什么大不了的事情.有的教师坚持接触的物体有弹性形变才有弹力,但是模型都是一定实际对象的简化,实际对象都是有弹性的.把图3(a)的圆盘当成弹性圆盘更有工程价值和教学意义.其实图1模型中墙面和地面当作了刚体处理,弹性形变为零,照样有弹力.再比如图3(b)中在水平力F的作用下,A和B发生匀速运动.有的教师坚持A和B之间没有摩擦力,笔者则认为“A和B之间摩擦力为零”的说法容易拓展.前者的理由是物体之间没有相对滑动,其实没有相对滑动也可以有摩擦力,图3(c)所示的纯滚动的轮子,在接触点就没有相互滑动,但是仍有摩擦力.我们要习惯于“零度,零势能,零弹力,零摩擦力”这些说法,它们不是没有对应的物理量,而是量值为零.采用这些说法,就容易将中学教材里静态的和简单的物理现象和规律拓展到有工程意义的复杂问题.
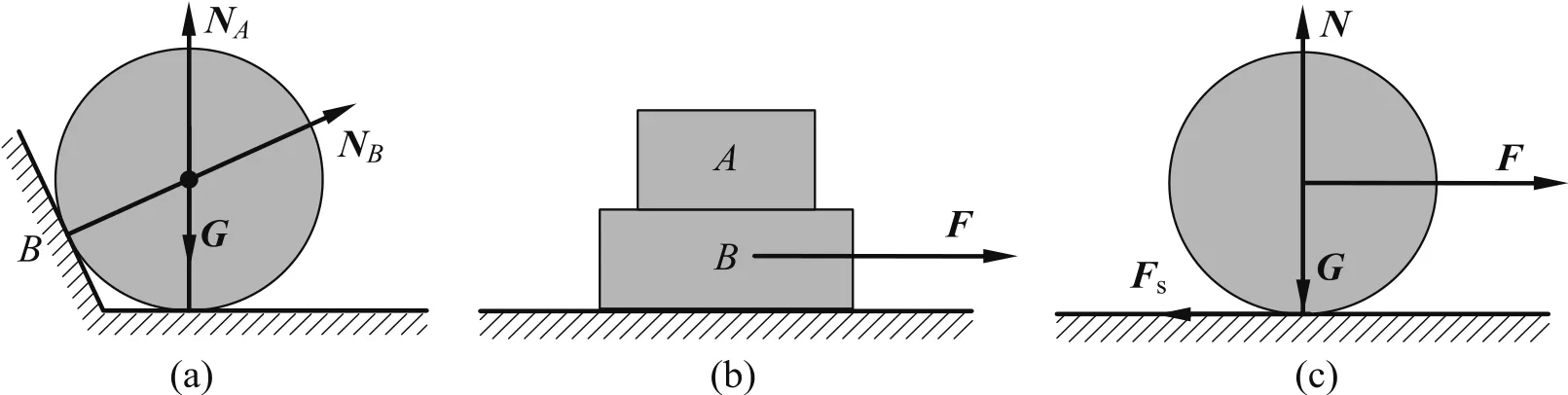
图 3
再比如有些教师强调“机械能守恒”要求动能和势能要有变化[29],笔者认为这完全没有必要.“机械能守恒”一方面是大自然规律的刻画,但更重要的是便于使用,而采用“动能和势能总和保持不变”有更大适用范围.其实,机械能守恒也是发展的、专业性的术语,并非终极、一统的概念.比如,牛顿时代的莱布尼兹研究过动能守恒,机械能中的势能直到1853年才由Rankine正式提出[30],而在这之前焦耳和迈耶已经建立了现代意义上的能量守恒与转化定律.此外,在科技表达方面,汉语模糊性本来就比英语要大一些,所以千万不要用文字游戏绊住喜欢物理的学生.
3 商榷
第1节讨论的例题频繁出现,笔者搜集到文献有26篇[1-26],其中最早一篇的模型不是两小球,而是两小车[7](直到最近还有把小球A理解成能降到地面的[25]).下面主要对文[1]和文[6]中有关内容,谈谈笔者的看法.
(1)叶文解法一式(7)和解法二式(4)之间差一个符号.如果能把角坐标的正转向规定好,就能避免这样问题.角坐标的起始边应为固定边.比如图2中的地面为起始边,而从地面到AB杆顺时针为角坐标的正方向.一阶导数和二阶导数转向都是沿角坐标的正转向.解法一的式(8)的角速度平方小于零,也是源于角坐标的正转向问题.解法二式(3)不涉及求导和积分,所以符号问题没有表现出来.形成良好的坐标习惯,在分析复杂问题时才不至于符号出错.
(2)叶文随后的论述“A脱离墙壁之后系统的重力势能仍在不断减小,而A在水平方向上的速度显然由零开始增加,所以B在水平方向的速度必然减少——这是一个非常重要的结论”的充分性不够.B在水平方向的速度必然减少是因为水平方向动量守恒和A速度的水平分量增加,与而之前的“A脱离墙壁之后系统的重力势能仍在不断减小”没有直接关系(叶文的表述易误导读者——认为“A脱离墙壁之后系统的重力势能仍在不断减小”为论证依据).基于极值方法几乎都存在这样“B速度最大”论证不充分问题[8-21],虽然本题中确实是极值.
(3)叶文解析三的基点法有限制条件:基点的加速度要为零.恰好本题在脱离瞬间B的加速度确实为零.如果不受限制地推广,那么来看初始时刻.在初始时刻,各处速度为零,角速度也为零,当然A绕B的向心加速度为零.按照这样演绎,可解得aA=0这个无厘头的结果.文献[22~24]所坚持的坐标变换法也存在同样问题.
(4)初文[6]的解析1论证了系统水平方向动量px最大,但进而简单地认为B球动量也最大.这时应该补充这样的论证:脱离时刻px向右,大于脱离前任一时刻,而脱离之后px不变(系统水平方向动量守恒),由于墙壁的限制作用,脱离之后短时间内A动量的水平分量只能向右,这只能让B的动量减少,以保证系统水平方向动量守恒,所以在脱离时刻B动量达到最大(这也是初文的解析2和3之基础).如果像图4这样的模型,则未必能够保证在A脱离时刻,B的动量最大.

图 4
(5)初文解析2中的A球相对C的水平速度是向左vB/2,而不是向右.
(6)在初文解析3的图5中,两个vB方向相反.vB作为矢量,在图中这样表示容易误解它的方向.
(7)本题的物理过程在脱离前后分为两个阶段,两个阶段的数学函数显然不同.如果对应的物理参数是连续的,那么从前一阶段向后推,取极限得到的脱离点的参数与从后一阶段向前推到脱离点的参数将是相同的.如果无法保证物理参数是连续性,则不能这样推断,比如图4所示的模型(再比如AB杆在初始放手之后和放手之前也不能这样推).本题的作用力在A脱离前后连续变化,相应的速度连续可微,所以能通过求导的方式找到临界脱离点.
4 结语
作者认为这种需要高度数学技巧的物理题目不宜作为高考模拟题.物理离不开数学,但中学阶段的物理教学应是通过简单的数学强调物理概念和物理学的美,而不是在现阶段就要求学生为了解物理题去花大量的时间来掌握某些数学“秘籍”.一方面这些“秘籍”让学生对物理有畏难情绪.另外一方面对物理的真正研究也不使用这些初等“秘籍”.优秀的物理教师应该让学生对物理感兴趣.只要学生能对物理有兴趣,将来大学或研究阶段,自然会下功夫把所需要数学工具学好.教师应该引导学生定性分析物理现象的本质,以及让学生初步了解将来物理研究所需要的通用工具.
希望上述观点能被教育评估者认可,被教育实施者认可.
[1]叶玉琴.一道力学题的求解及感悟[J].中学物理,2011,29(21):20-22.
[2]肖光宏.也谈“一道力学题的求解及感悟”[J].中学物理,2012,30(19):51-52.
[3]鲁良根.补议《一道力学题的求解及感悟》[J].中学物理,2012,30(19):49.
[4]赵杰.巧用三角函数再解这道力学题[J].中学物理,2012,30(1):67-68.
[5]汪飞.《对一道力学题的求解及感悟》中例题解法的再补充[J].中学物理,2013,31(17):48-49.
[6]初毅,豆诗霞.“华山险路”—只此一条难题求解—岂能有限[J].中学物理,2012,30(13):70-72.
[7]李虎驼.严谨思维的解题功能[J].中学物理教学参考,1998,27(3):14-15.
[8]袁少铄.利用动量定理的独立性解答物体分离问题[J].广东教育,2005,(7-8):70-71.
[9]汪志杰.巧用机械能守恒定律求解连接体问题[J].高中生,2006(18):51-53.
[10]周琪兵.牵连物体的速度关系[J].物理教师,2007,28(7): 66-67.
[11]刘文韬.几种三角函数极值的物理应用[J].物理教师,2007,28(1):10-11.
[12]张庆枝.用数学方法求物理量的极值[J].高中数理化,2009(8):39-42.
[13]张士军.利用均值不等式求解物理极值问题[J].教师,2009(6):74.
[14]李建华.用基本不等式巧解物理最值问题[J].中小学实验与装备,2010,20(5):2-3.
[15]金彬.不等式在物理中的应用[J].考试(高考理科版),2010(2):44-45.
[16]满桂花.利用微积分知识求解高中物理中的疑难问题[J].物理教师,2011,32(7):64-65.
[17]马广明.挖深层联系.解复杂问题[J].物理教学,2012,34(9):50-51.
[18]孙靖月.物理解题方程的求解策略[J].数理化解题研究(高中版),2014,(10):41-42.
[19]李星旭.物理解题方程的求解策略[J].考试周刊,2014(17):142-143.
[20]叶玉霞,王秀云.几种物理问题的求解策略[J].考试周刊,2014(7):139.
[21]陈华.墙壁上物体滑落的临界问题分析[J].物理教师,2015,36(4):66-67.
[22]汪飞.应用均值不等式巧解极值题[J].物理教学,2013,35(5):54-55.
[23]汪飞.浅谈转换参考系在一类牵连物系问题中的应用[J].物理教师,2014,35(1):88-89.
[24]邱刚.巧用错题激发兴趣培养能力—对一道科学性错误试题教学价值的探讨[J].物理教师,2014,35(8):94-95.
[25]徐君生.动能定理的理解与应用[J].高中数理化,2013(19):31-34.
[26]查清哲.数形结合,巧用刚体转动知识解一道竞赛题[J].物理教师,2016,37(2):97.
[27]哈尔滨工业大学理论力学教研室.理论力学(Ⅰ)[M].7版.北京:高等教育出版社.2009,7:284.
[28]陈奎孚.理论力学自主学习解题辅导[M].北京:中国农业大学出版社,2014(12):286-289.
[29]李庆国.机械能守恒吗?——对“机械能守恒定律”几种错误理解的讨论[J].物理教学探讨,2010,28(6):39-40.
[30]Rankine.On the general law of the transformation of energy[J].Philosophical Magazine Series 4.1853,5(30):106-117.
HIGH SCHOOL PHYSICS EDUCATION SHOULD HIGHLIGHT THE CORNER STONE KNOWLEDGE AND UNDERLINE THE UNIVERSAL APPROACH
Chen Kuifu
(College of Science,China Agricultural University,Beijing 100083)
A sophisticated mechanics problem was discussed by many authors.In this paper a solution is presented,which can be assimilated with the requisite of high-school level knowledge of physics and mathematics.It is argued that physics education should nourish students with the beauty of physics,and improve their capability and ambition to appreciate the beauty of physics.The bad practice of examination orientation by cramming solutions to some special problems should be avoided in physics education.Some comments were made on the statements which appeared in literature discussing the aforementioned mechanics problem.
education;pedagogy;physics;the 2ndNewton law
2016-03-27;
2016-04-08
陈奎孚,男,教授,主要从事力学、生物物理科研和教学工作.Chen KuiFu@Hotmail.com
陈奎孚.中学物理教育应该强基础重通适——一位大学教师视角[J].物理与工程,2016,26(4):22-26.
