定日镜镜面偏心距误差仿真分析与补偿算法

沈 磊，姜 晨

(上海理工大学 机械工程学院，上海200093)



定日镜镜面偏心距误差仿真分析与补偿算法

沈 磊，姜 晨

(上海理工大学 机械工程学院，上海200093)

根据太阳能塔式发电定日镜高精度控制的需求，主要研究镜面偏心距对定日镜跟踪精度的影响，对其所造成的跟踪误差进行几何建模与仿真分析，研究结果表明镜面偏心距误差对追踪精度影响显著。为此提出一种实现镜面偏心距误差补偿的反射算法，利用实际定日镜实验装置的工作参数进行仿真计算与分析。分析结果表明该反射算法计算的姿态角误差小，计算量低，不仅能够很好地补偿镜面偏心距所造成的误差，而且特别适合植入嵌入式或者上位机控制平台，具有理想的应用前景。

定日镜；镜面偏心距；反射算法；误差分析与仿真

0 引言

定日镜是塔式太阳能发电系统的重要装置，主要功能是跟踪太阳，将太阳光线聚焦反射到集热器，以加热管内流动的水工介质产生过热蒸汽来推动汽轮机进行发电，是能量传递的关键部件[1，2]。定日镜聚光追踪精度的高低将直接影响系统的发电效率和集热器的安全运行，因此提高定日镜的精度具有重大意义[3]。大多数定日镜采用方位-俯仰(方位轴-高度轴)双轴追踪方式。定日镜主要由镜面(反射镜)、镜架(支撑结构)、跟踪传动装置和控制系统组成[4，5]。除了控制系统之外，其余都属于机械装置。机械装置难免会存在各种误差，会对定日镜的追踪精度造成影响。

Stone和Jones(1999)描述了几种(机械装置)追踪误差，包括三种主要的几何误差：方位轴倾斜误差(基座倾斜误差)、镜面安装误差和编码器反馈误差[6]。Khalsa等人(2011)根据前人的结果总结了8种定日镜追踪误差，主要包括：基座(方位轴)倾斜ε1和ε2；编码器(传感器)反馈的高度角和方位角位置信号的偏差ε3和ε4，方位轴和高度轴的线性误差ε5和ε6，包括驱动轮和齿轮的传动误差；驱动轴的非正交性ε7；镜面倾斜误差ε8[7]。Guo等人(2011)在综合考虑了镜面偏心距(d)和其他8种定日镜的误差之后给出了定日镜的精确追踪角度计算方法[8]。

镜面偏心距是指定日镜中心点与镜面中心的距离。理论的定日镜追踪角度计算没有考虑镜面偏心距，认为定日镜的中心(旋转中心点)就是镜面的中心。因为理论上在计算反射向量时认为是从定日镜中心到目标靶中心，实际的反射情况是从镜面中心，因此就出现了系统误差。而上述介绍的8种追踪误差是由于定日镜装置本身安装所造成的误差，可以通过提高安装精度大幅度降低其对跟踪精度的影响，而镜面偏心距无法通过后期调试来降低或消除，因此，定日镜镜面偏心距对跟踪精度的影响必须重点关注。如果在反射算法中加入误差补偿，形成更精确的反射算法，对定日镜的追踪精度提高具有积极意义。本文根据塔式发电站定日镜的工作原理，对因镜面偏心距造成的定日镜追踪角度(姿态角)误差进行系统的仿真分析，并将分析结果反馈到反射算法，实现一种高精度的镜面偏心距补偿反射算法。

1 定日镜常规姿态角(高度角与方位角)求解

塔式发电站定日镜的工作反射示意图如图1。定日镜的镜面通过双轴的转动调节实现对太阳光线的追踪，将太阳光线反射到一个固定的目标靶(集热器)上。如图1所描述的虚线部分，是未考虑镜面偏心距的常规反射的情况。

图1 定日镜镜面反射示意图

定日镜中心点O(理论反射中心点)坐标：(0，0，0)。镜面中心为M。已知太阳高度角(Ze)，方位角(Az)，故太阳光线单位向量为：

S=(-cosZe×sinAz,-cosZe×

cosAz,-sinZe)

(1)

已知目标靶中心点坐标T为(a，b，c)，因此理论反射单位向量为

可求得理论镜面单位法向量为[6]

(2)

设N=(Xr,Yr,Zr)，则可以得出定日镜的高度角α与方位角β：

(3)

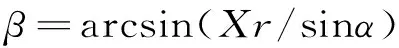
(4)

理论反射光线中心是到达T点，但是由于镜面偏心距的存在，反射光线中心到达了T1点。

如图1的实线部分，通过对定日镜的姿态角进行微调整，最终使得反射光线中心到达T点。下面讨论考虑镜面偏心距时的反射位置算法。

2 带镜面偏心距补偿的精确求解

为了减少定日镜追踪的误差，在充分考虑镜面偏心距时，利用空间几何建模，重新对定日姿态角进行精确求解。如图1的实线部分，设镜面中心坐标M=(x，y，z),反射单位向量为

设OM=d，即为镜面偏心距。

故精确的镜面法向量为N′=R′-S=k(x,y,z)，其中k为一个常数，即为

(-cosZe×sinAz,-cosZe×

cosAz,-sinZe)=k(x,y,z)

(5)

(6)

展开之后是一个四元非线性方程组，求解该方程组可获得高精度的偏心距补偿坐标，但该算法计算量大，不适合植入嵌入式和上位机平台。本文利用该算法作为对比手段，用于评估其他算法的误差大小。

图2 定日镜实验平台

利用2015年4月29日上海某地的太阳位置数据进行验证。从早上6点到晚上6点，每隔半小时取一组太阳位置数据。根据现有的定日镜实验平台(镜面3.75m2)如图2，建立三维空间坐标。以定日镜旋转中心点为坐标原点，正东为x轴，正北为y轴，竖直向上为z轴。测得的目标靶中心点坐标为(-419.63，618.6，175.84)，单位为cm，镜面偏心距d测得为26cm。如图3是当天精确反射算法仿真得到的定日镜的姿态角的精确值。

图3 定日镜精确姿态角

采用未考虑镜面偏心距的反射算法和同样的实验平台参数，得到一组定日镜姿态角数据。将这组数据与图3的精确数据进行误差比较，如图4，在不考虑镜面偏心距的情况下，定日镜的姿态角误差最大能超过1°，这个误差远远超过定日镜的设计误差，因此如何对其实现补偿极为关键。

图4 未校正定日镜姿态角误差

不同定日镜的镜面面积不同，其镜面偏心距d的大小也不同，d的大小会对定日镜姿态角的误差造成影响。图5是对不同d的定日镜姿态角误差进行仿真分析，可以发现，d越大，所造成的定日镜追踪角度的误差也就越大。因此，需要对镜面偏心距所造成的误差进行补偿。

图5 不同镜面偏心距定日镜的姿态角误差比较

3 一种带镜面偏心距补偿的反射算法

为了实现定日镜的误差补偿，在计算定日镜姿态角的反射算法中实现镜面偏心距补偿功能，是确保定日镜跟踪精度的一种有效、可行的方法。

如图6，定日镜从初始位置(高度角和方位角均为0)开始，首先按照理论反射算法(不考虑镜面偏心距)进行偏转，定日镜第一次到达位置，也就是理论的方位。此时的定日镜单位法向量为N，由于定日镜中心点坐标为(0，0，0)，可以求出此时定日镜镜面中心点坐标M。由(2)式可得：

M=(Xr×d,Yr×d,Zr×d)

(7)

然后以M为定日镜中心点，此时反射单位向量R1为(T-M)。而太阳入射单位向量S不变，根据R1和S求出第二次定日镜镜面单位法向量N1。

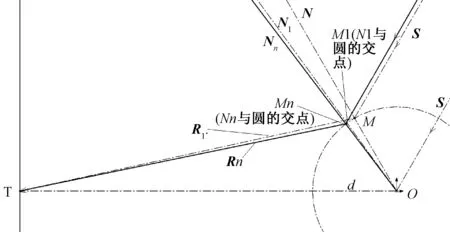
图6 迭代反射示意图

(8)

为第一次迭代。根据式(3)和(4)求出高度角α1和方位角β1。

接下来进行第二次迭代。根据式(8)得出N1=(Xr1,Yr1,Zr1)，则第一次迭代的镜面中心坐标：

(9)

然后以M1为定日镜中心点，此时反射单位向量R2为(T-M1)。而太阳入射单位向量S不变，根据R2和S求出第二次定日镜镜面单位法向量N2。

(10)

根据(3)和(4)可求出定日镜的高度角α2和方位角β2。

可以继续按照这种方法进行迭代计算，求出第n次的镜面中心点坐标Mn和反射单位向量Rn(图6中实线标出)，得出第n次的定日镜镜面单位法向量Nn：

(11)

为第n次迭代。并根据(3)和(4)式算出此时定日镜的高度角αn，方位角βn。

同样利用上述实验条件进行Matlab仿真，分别进行一次迭代和二次迭代的计算，得到两组定日镜的姿态角，与精确的定日镜的姿态角(图3)进行误差比较，一次迭代的误差与二次迭代的误差分别如图7与图8。可以发现，一次迭代的最大误差在0.01°左右；二次迭代最大误差在0.000 1°左右。一般情况下，一次迭代已经基本满足要求，特别精确的条件下二次迭代完全满足要求，不需要三次以上的迭代计算。

表1是几种反射算法的计算量的比较。可以发现，增加一次迭代的反射算法比常规反射算法的计算量增加不到一倍，二次迭代比一次迭代计算量的增加亦是如此。因此，迭代算法既能保证定日镜跟踪精度，又满足嵌入式的低计算量的需求，适合应用在嵌入式系统中。

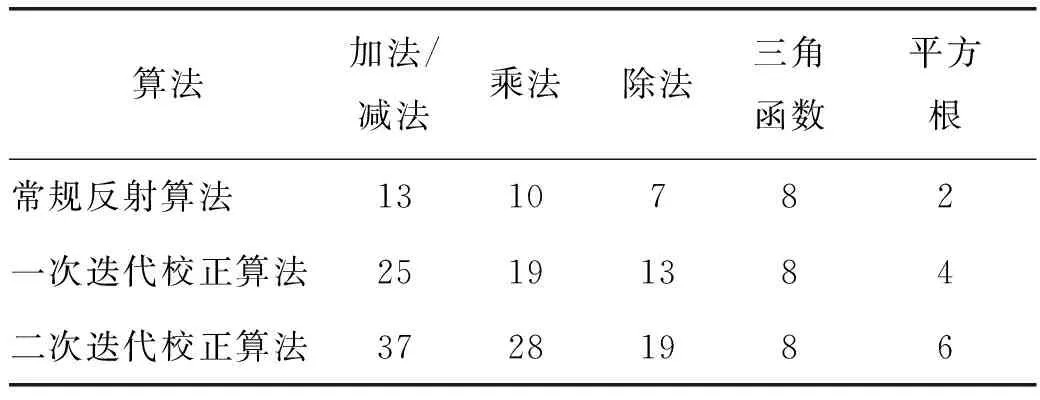
表1 算法计算量比较

图7 一次迭代定日镜姿态角误差

图8 二次迭代第定日镜姿态角误差

4 结论

本文对定日镜的各种机械跟踪误差进行了介绍，针对因镜面偏心距所造成的误差进行了系统的分析与仿真，传统未考虑偏心距的反射算法得出的定日镜姿态角最大误差会超过1°，而且随着镜面偏心距的增大，定日镜的姿态角误差也会相应地增大。为了解决因镜面偏心距所造成的定日镜的追踪误差，本文给出了精确的定日镜姿态角的计算方法，用于评估其他反射算法的误差大小。同时提出了一种有效的带镜面偏心距误差补偿的反射算法，经过仿真验证，计算出的姿态角误差小、计算量低、不仅能够有效确保定日镜跟踪精度高，尤其适合大规模应用在嵌入式控制系统中。

[1]王孝红, 刘化果.塔式太阳能定日镜控制系统综述[J].济南大学学报(自然科学版), 2010, 24(3): 302-307.

[2]塔式太阳能电站定日镜场的建模与仿真[J]. 中国电机工程学报, 2012, 32(23): 90-98.

[3]孙飞虎, 郭明焕, 白凤武,等. 定日镜跟踪纠偏策略综合应用研究 [J].太阳能学报, 2014, 35(7): 1272-1279.

[4]IGEL E A,HUGHES R L.Optical analysis of solar facility heliostats[J]. Solar Energy, 1979(22):283-295.

[5]CHEN Y T,CHONG K K,LIM C S,et al.Report of the first prototype of non-imaging focusing heliostat and its application in high temperature solar furnace[J].Solar Energy, 2002, 72(6): 531-544.

[6]STONE K W, JONE S A.Analysis of solar two heliostat tracking error sources[J]. 1999.

[7]KHALSA S S,H C K,ANDRAKA C E.An automated method to correct heliostat tracking[J].Proceedings of SolarPACES[C]. Granada, Spain, 2011.

[8]GUO M H,Wang Z F,ZHANG J H, et al.Accurate altitude-azimuth tracking angle formulas for a heliostat withmirror-pivot offset and other fixed geometrical errors[J].Solar Energy, 2011, 85(5): 1091-1100.

SHEN Lei, JIANG Chen(Mechanical Engineering School，University of Shanghai for Science and Technology，Shanghai 200093, China)

Erroranalysis and Compensation Algorithm for Heliostat Tracking with Mirror-Pivot Offset

In view of the requirements of high precision control in solar power tower heliostat, this paper presents an investigation on the influence of the mirror-pivot offset on the heliostat tracking error. The heliostat tracking error is geometrically modeled, by which the simulation analysis is conducted. The simulation results show that mirror-pivot offset has a significant effect on the tracking accuracy of heliostat. Therefore, a new reflection algorithm is developed to compensate the mirror-pivot offset. Using the device parameters of actual experimental heliostat, the presented reflection algorithm is verified. The analysis results show that the reflection algorithm is effective to compensate the heliostat tracking angle errors. In view of the low calculation amount, it is a suitable reflection algorithm for embedded system and PC control platform.

heliostat; mirror-pivot offset;reflection algorithm;error simulation and analysis

2016-05-05。

沈磊(1990-)，男，硕士研究生，主要研究方向是太阳能控制系统，E-mail：shenlei820843@163.com。

TK513.1

A DOI:10.3969/j.issn.1672-0792.2016.09.006