连续系数一维倒向随机微分超前方程的解
2016-11-12周会会
周会会,梅 端
(广东海洋大学理学院,广东 湛江 524088)
连续系数一维倒向随机微分超前方程的解
周会会,梅端
(广东海洋大学理学院,广东 湛江 524088)
证明了具有连续系数的一维倒向随机微分超前方程(超前BSDE)存在适应解,并得到了最小解的存在性。
倒向随机微分超前方程;适应解;连续系数
Pardoux和Peng[1]引入了非线性倒向随机微分方程(BSDE),并证明了在Lipschitz条件下非线性BSDE适应解的存在唯一性。BSDE在随机控制、偏微分方程、数理金融、经济等领域都有着广泛的应用,吸引了众多学者对其研究。例如:Lepeltier和Martin[2]研究了具有连续系数的BSDE适应解的存在性及最小解的存在性;Jia[3]研究了具有连续系数的BSDE解的结构;El Karoui,Peng和Quenez[4]给出了具有Lipschitz条件的BSDE适应解的比较定理;Liu和Ren[5]讨论了具有连续系数的BSDE解的比较定理等。
Peng和Yang[6]引入了一类新的倒向随机微分方程,即倒向随机微分超前方程(超前BSDE),并证明了在Lipschitz条件下超前BSDE适应解的存在唯一性及解的比较定理,随后,陈丽[7]研究了超前BSDE中Z的性质,许哓明[8]研究了超前BSDE的反射解等。
本文主要研究了如下形式的超前BSDE。即
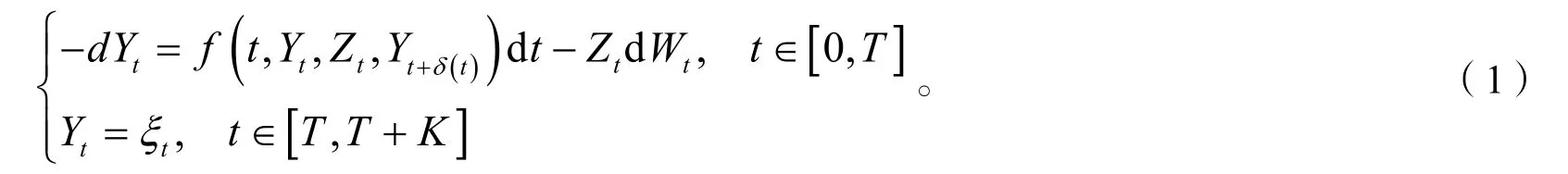
1) 存在常数
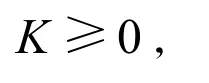
使得
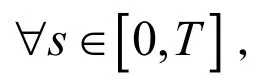
有
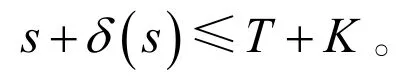
2)存在常数
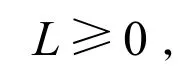
使得
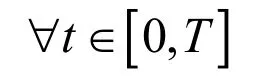
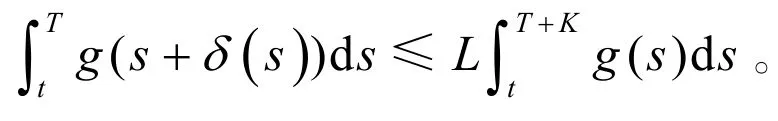
在 Liu和 Ren[5]论文的启迪下,如果把超前BSDE所满足的Lipschitz条件减弱,只让其满足线性增长条件,所对应的超前 BSDE是否存在适应解?本文主要讨论具有连续系数的一维超前BSDE适应解的存在性,并得到了最小解的存在性。
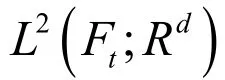
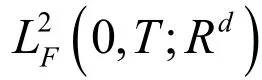
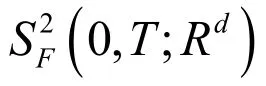
1 具有连续系数的超前BSDE适应解的存在性
引理 1[2]令是具有线性增长的连续函数,即存在常数K0<∞,使得,
有
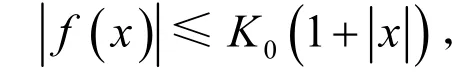
那么下面的函数列
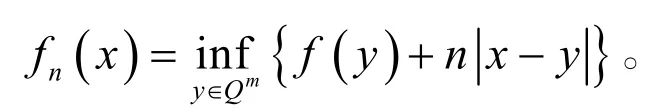
(i)线性增长条件:
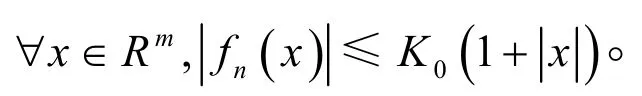
(iii) Lipschitz条件:
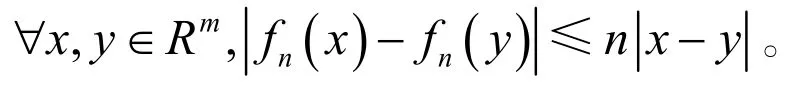
(iv) 强收敛性:若
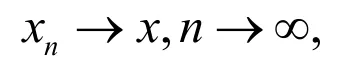
那么
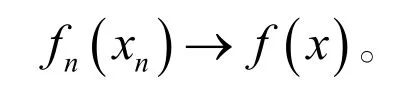
引理2[9]在引理1的假设下,设m=1,f关于x单调增,则
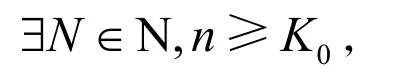
使得当n>N时,引理1给出的fn均关于x单调增。
定理1
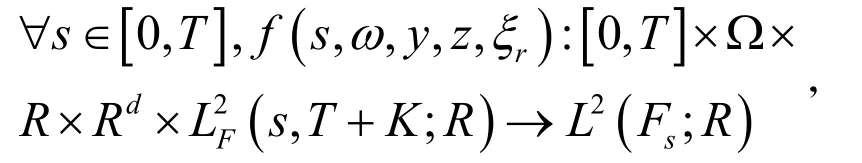
设f满足:
(H1) 线性增长条件:
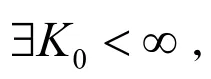
对
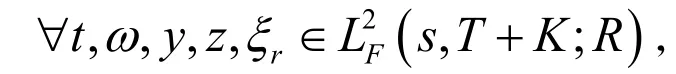
有
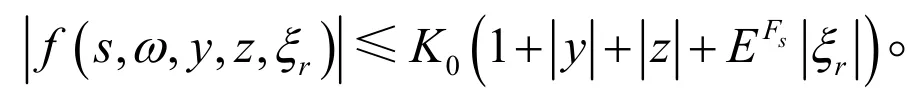
(H2) 对于固定的s,ω,y,z,f( s,ω,·,·,·)连续且f( s,ω,y,z,·)递增。
则对任意给定的终端条件
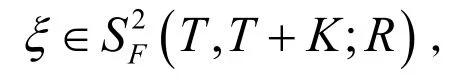
超前BSDE式(1)有适应解,即:∃tF-适应的过程
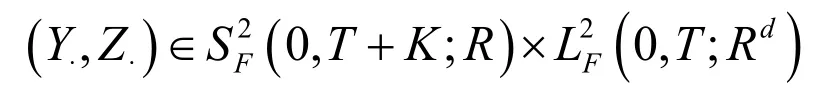
满足方程式(1)。
证明:给定(t,ω ),由引理1可知函数f对应函数列
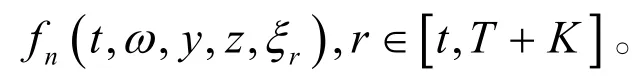
考虑函数
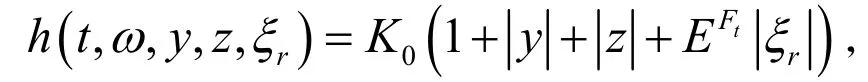
那么函数fn和函数h都是Lipschitz函数。又由于
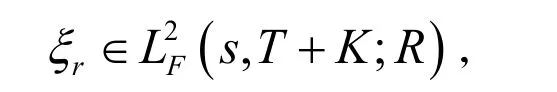
由[6]中定理4.2可知下面的超前BSDEs在
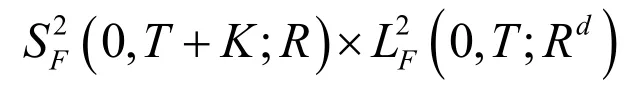
上有唯一解。
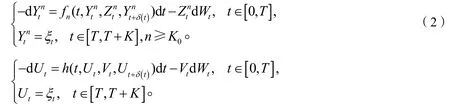
由(H2)及引理2可知fn关于递增且关于n单调,由参考文献[6]中的定理5.4可得,
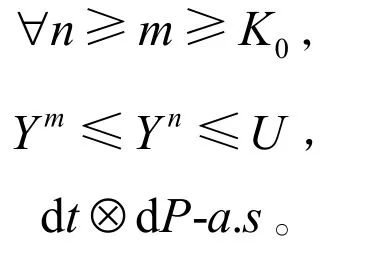
所以存在仅依赖于
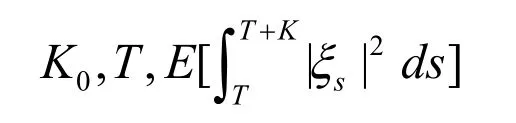
的常数B使得
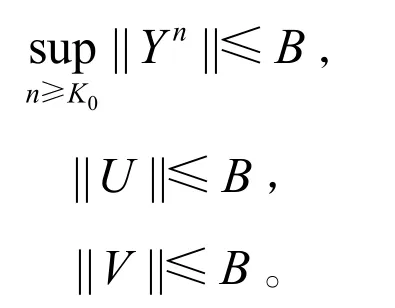
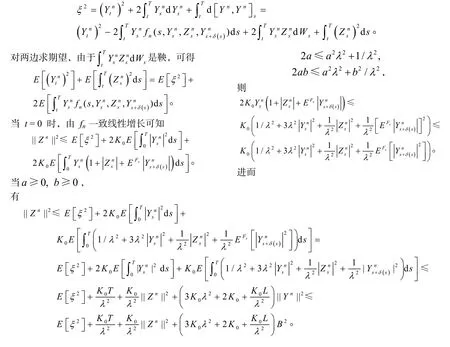
由于
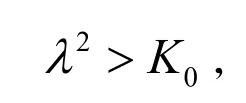
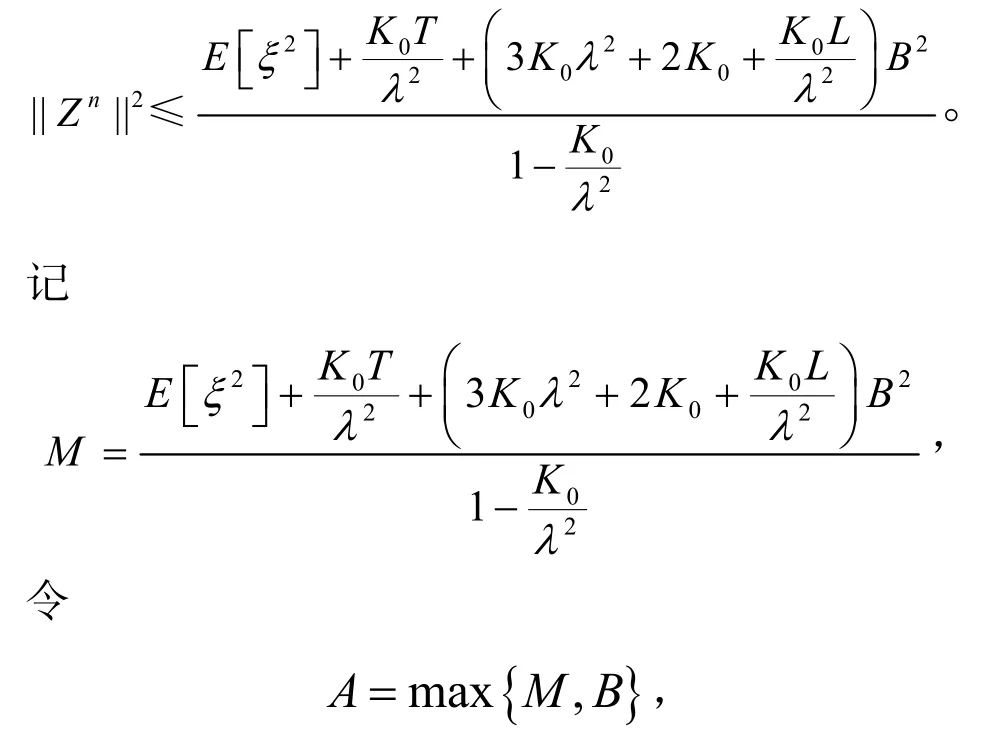

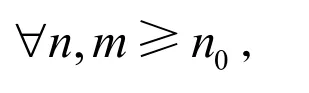
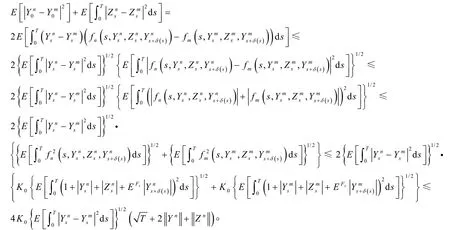
则存在常数C,使得
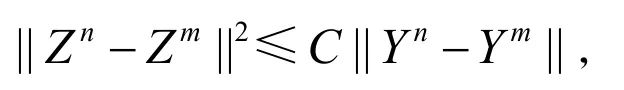
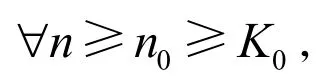
我们有
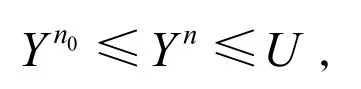
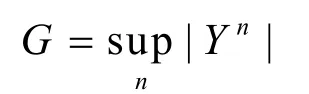
另一方面,由于
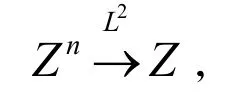
取一子列可得

且
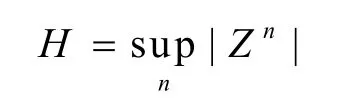
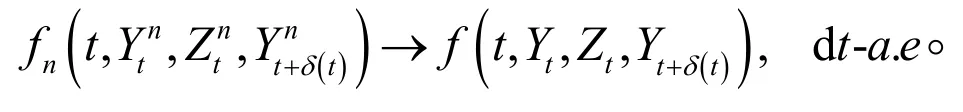
且
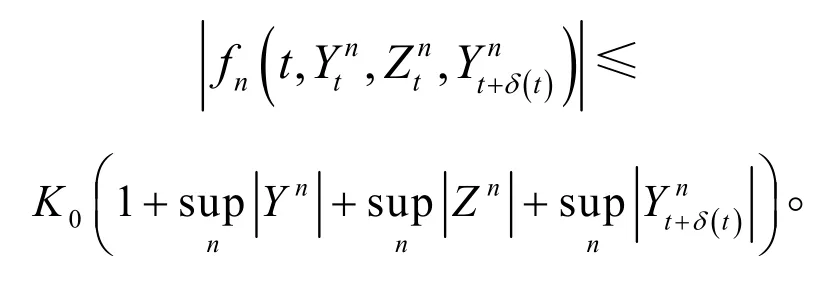
由一致收敛定理可得,当n→∞时,
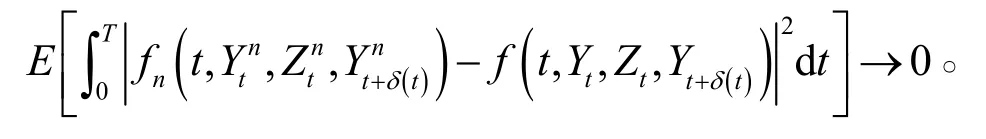
由随机积分的连续性可得,
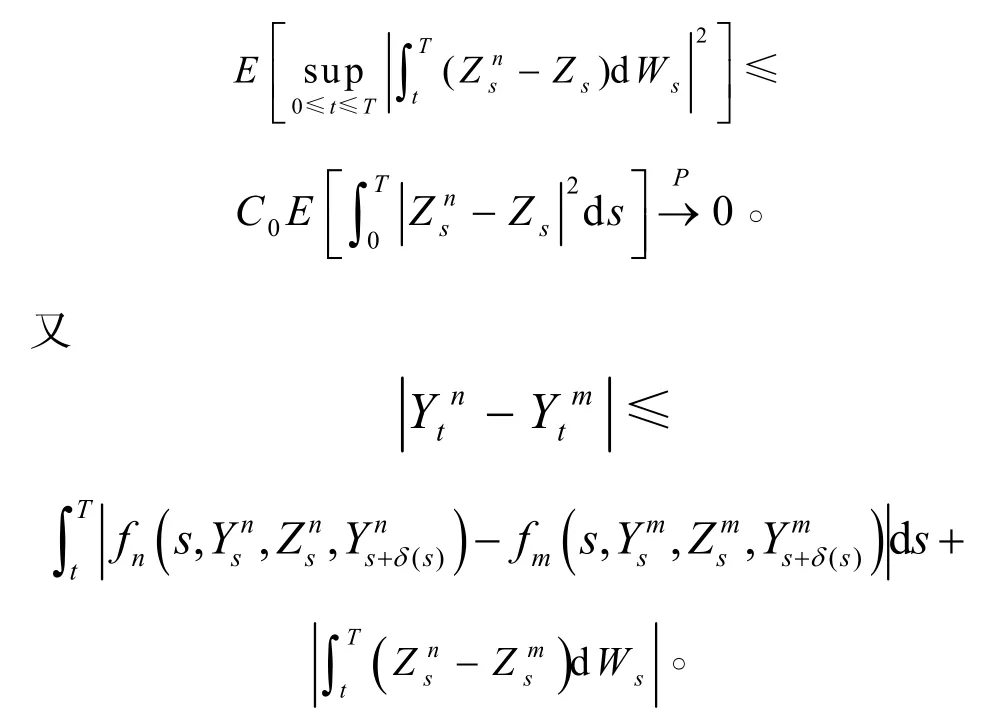
对m取极限,对t取sup,可得

例:考虑超前BSDE,
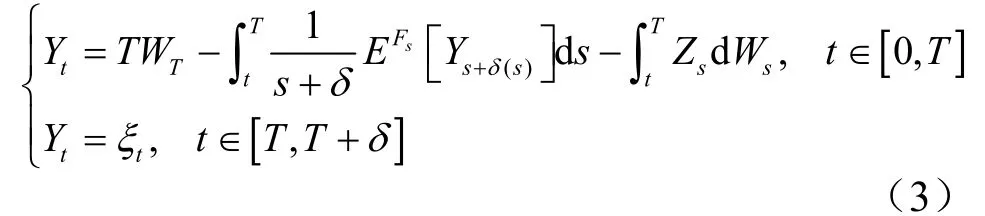
其中δ≥0为给定常数。容易验证方程式(3)中f 满足线性增长条件,且有解
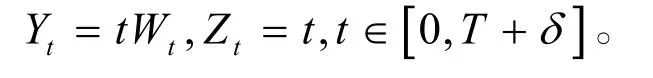
2 结 论
考虑到具有连续系数的BSDE存在唯一适应解,在此基础上,进一步研究了超前BSDE,从理论上得到了具有连续系数的超前BSDE存在适应解,并得到了最小解的存在性,对超前BSDE有了进一步的认识。
[1]PARDOUX E,PENG S G.Adapted solution of a backward stochastic differential equations[J].Syst Cont Lett,1990,14(1):55-61.
[2]LEPELTIER J P,SAN M J.Backward stochastic differential equations with continuous coefficient [J].Stat Prob Lett,1997,32(4):425-430.
[3]JIA Guangyan.On the set of solutions of a BSDE with continuous coefficient[J].C R Acad Sci Paris ,2007,344(6):395-397.
[4]EL Karouin,PENG S G,QUENEZ M C.Backward stochastic differential equations in finance[J].Math Fin,1997,7(1):1-71.
[5]LIU J C,REN J G.Comparison theorem for solutions of backwardstochasticdifferentialequationswith continuous coefficients[J].Stat Prob Lett,2002,56(1):93-100.
[6]PENG S G,YANG Z.Anticipated backward stochastic differential equations[J].Ann Prob,2009,37(3):877-902.
[7]陈丽.超前BSDE中Z的性质及其在时滞随机控制中的应用[J].山东大学学报(理学版),2010,45(4):16-20.
[8]许哓明.超前倒向随机微分方程的反射解及相应的最优停时问题[J].山东大学学报(理学版),2013,48(6):14-17.
[9]杨哲.超前BSDE及SDE中的相关结果[D].济南:山东大学,2007.
(责任编辑:任万森)
Solutions of One-dimensional Anticipated Backward Stochastic Differential Equations with Continuous Coefficient
ZHOU Hui-hui,MEI Duan
(College of Science,Guangdong Ocean University,Zhanjiang 524088,China)
In this paper,it is proved that the existence of a solution to one dimensional anticipated backward stochastic differential equations where the coefficient is continuous.The existence of a minimal solution is also obtained.
anticipated backward stochastic differential equations; Adapted solutions;continuous coefficient
O211.6
A
1673-9159(2016)04-0078-05
10.3969/j.issn.1673-9159.2016.04.013
2016-04-29
广东省高校创新强校工程项目(2014KQNCX080)
周会会(1984—),女,讲师,硕士,主要从事金融数学、倒向随机微分方程的研究。E-mail:huihui0325@126.com
