土质隧道考虑时空效应的施工力学行为分析

杨军平，王沾义，李盛南，唐伟

(1.桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004;2.贺州市住房和城乡建设局，广西 贺州 542800)



土质隧道考虑时空效应的施工力学行为分析

杨军平1，2，王沾义1，李盛南1，唐伟1

(1.桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004;2.贺州市住房和城乡建设局，广西 贺州 542800)

通过对膨胀土隧道开展动态施工力学的物理模型试验，得出各测点在洞室开挖和衬砌支护条件下的围岩应力—时间响应曲线。根据响应曲线对施工过程中围岩随时间及空间条件的变化而呈现的力学响应及行为表现进行分析，并将响应曲线的发展变化趋势按开挖和支护分为不同阶段，其中开挖过程分为零增长、微增长、急剧下降 、缓慢减小和相对平稳5个阶段；支护过程分为急剧增长和缓慢下降2个阶段。此外，通过对隧洞竖向线及水平腰线上距洞室边缘不同距离测点的分析，表明随着距离的增大，由隧洞开挖导致的围岩应力释放量减少，释放速率减缓，力学响应敏感度降低，衬砌支护对围岩力学特性的影响也逐渐减弱。

土质隧道；时空效应；应力释放；回弹位移；响应曲线

隧道属于地下结构的一种，较之于一般地面建筑物具有明显的区别。该区别主要表现在其施工修筑及后期工作一般都是处在具有一定应力历史和应力场的围岩环境中[1]。隧道在开挖施工前，岩体中本身客观存在着一个经历长期固结过程而形成的初始应力场，且随应力场深度的不同其应力势能各不相同。隧道尤其是软弱土质围岩隧道的开挖，使得初始地层应力场的平衡状态遭到较大程度的破坏[2]。隧道开挖将原本承受一定荷载的岩体挖出，致使洞室周边围岩的边界条件由原来初始地应力状态下的固定稳态边界转变成扰动后的自由动态边界，从而引起围岩发生相应的力学响应及行为表现，这一方面表现在围岩应力释放引发应力重分布，另一方面使洞周围岩产生向洞室内空方向的位移。但因开挖面具有一定的空间约束效应，使得应力释放及围岩位移现象不会在瞬间完成也不会无休止进行下去直至隧洞坍塌[3]，因为隧道会充分利用这种空间效应及结合洞室顶部的压力拱效应[4]形成自承能力。而当衬砌施筑并形成有效的围岩支护体系后，边界条件再次变化，围岩的位移发展将受到限制，但是在软弱围岩的流变时效特性下，整个隧道结构系统中的围岩应力，还将继续发生调整寻求新的平衡稳定状态。

目前，在上述围岩位移及应力释放的隧道施工力学的研究过程中，大部分都集中于隧道开挖对围岩位移的影响研究，如陈建勋等[5]对黄土隧道的施工变形进行了现场测试；扈世民等[6]结合数值模拟和现场试验，分析了台阶法施工时的围岩变形特征；蒋树屏等[7]对二车道公路隧道的围岩位移开展了模型试验研究；Hwang等[8-9]通过数值模拟的方式对基于时空效应的隧道施工进行了相关研究，并取得了不少具有实际价值的研究成果。在围岩应力的研究方面，吴梦军等[10]开展了连拱隧道的模型试验研究，绘制了应力释放比率的历时曲线，并认为开挖面前方存在围岩压力增压区。赵勇等[11]通过对隧道施工过程中荷载变化规律的研究，发现开挖面的推进对洞周围岩径向荷载的释放起主要影响。此外，王清标等[12-13]，还对膨胀土区域的隧道进行了一定的研究，也得出了一些颇具价值的理论成果。然而美中不足的是，上述研究少有对整个施工过程中应力释放的发展变化过程进行描述和分析。而对软弱土质隧道在整个应力释放过程中的施工力学行为进行深入研究，有利于了解该类隧道在隧洞开挖及衬砌支护的动态施工过程中，围岩随边界条件的改变而做出的基于时空效应的施工力学响应及行为规律[14]。本文拟通过开展以膨胀土隧道为代表的软弱土质隧道的物理模型试验，考虑开挖面空间支撑效应和流变时效特性的耦合效应，对软弱土质隧道的施工力学特性进行分析，描述洞室开挖和衬砌支护时围岩的应力发展变化规律及力学响应和行为表现，并对各阶段围岩应力释放率、应力影响深度进行分析，以对同类地质条件下的隧道施工提供借鉴和参考。

1　模型试验

1.1工程资料

某隧道由左右2个单洞双车道隧道组成，隧洞净宽为9.75 m。隧道围岩为第三系弱膨胀性亚黏土，稳定性较差，隧洞施工开挖时，拱部及侧壁时有坍塌或失稳现象发生。隧道围岩膨胀土物理力学指标见表1所示，土样命名为高液限黏土，具有弱膨胀性。

1.2围岩材料

本模型试验所用围岩材料均为取自广西南宁畜牧研究所水牛养殖场附近的膨胀土，取土深度为50～70 cm，外观棕黄色，呈硬塑状态，并夹有灰白色黏土，含水量较大。以膨胀土代替相似材料制作隧道模型，其优势在于有效降低相似材料与实际工程材料之间的差异，使试验结果更接近于实际。此外，该地区的膨胀土主要由第三系湖相沉积泥岩、粉质砂岩及其风化残积物形成，局部则由上述岩土风化物经流水搬运冲积形成。其基本物理力学指标见表1，表中密度、凝聚力、摩擦角、泊松比及变形模量均是在模型成型后取样测得。从表1可知，隧道模型的围岩各物理力学指标均与原型较为接近。根据文[15]中各级土质围岩的基本物理力学参数表可知成型后的围岩等级为Ⅴ级，且由自由膨胀率知其具有弱膨胀性。

1.3试验设备简介

本试验所有测点的围岩应力均是通过高速静态应变测试系统而获得，该测试系统主要由电阻应变式土压力盒、高速静态应变仪和计算机3部分组成，可对围岩应力变化值实施自动连续的实时采集。其中高速静态应变仪型号为DH3818-2，该应变仪可广泛用于土木、交通、机械等领域，若配接其他合适的应变式传感器，还可对位移、温度等物理量进行量测。该仪器测试应变范围±19 999 με；分辨率为1 με；自动平衡范围±15 000 με；灵敏度系数K=2。土压力盒采用长沙翔昊电子科技有限公司生产的XHZ-403型电阻应变式土压力盒(见图2)，其和DH3818-2采用全桥方式连接。土压力盒外观尺寸为Φ30×13 mm，量程为0.3 MPa，分辨率为≤0.05%F·S。该系列土压力盒较为适用于隧道等地下结构工程的动、静态测试，又因其体积小、灵敏度高的特点在室内模型试验或较小比例的模型试验中的工作性能尤为突出。

表1　材料的物理力学参数Table 1 Physical and mechanics parameters of material

1.4模型箱设计

模型箱由前、后大面板和左、右侧面板通过螺栓栓接而成，其中各板均为100 mm厚的高强钢板且端部焊接有角钢。模型箱主要是作为隧道模型夯筑时的模具以及为围岩提供边界约束条件。由于本试验模拟的是平面应变问题，故模型箱沿隧洞轴线方向的设计厚度取40 cm。另外，按试验要求隧洞直径设计为18 cm，取围岩深度为3～5倍洞径，从而确定模型箱其他两个方向净空尺寸为110 cm×110 cm。根据原型尺寸和模型设计尺寸并参照文[16]，可以得出几何相似比Cl=54.17，容重相似比Cγ=1.01，Cc=1.97，CE=1.35。

1.5隧道模型成型

膨胀土取回后，经翻晒、风干、碾细、过2 mm筛等工序测得风干含水率，通过分层洒水、均匀混合的方法配成所需含水率的重塑土。并按控制干密度1.6 g/cm3和重塑土实测含水率26.43%进行模型的夯筑。

夯筑前，根据控制干密度和重塑土实测含水率计算每2 cm厚为一层所需的土量，并通过人工进行分层夯实。夯筑过程中，各土压力盒均根据预先设计好的测点位置，按要求依次埋置于相应部位，因模型及试验条件左右对称，故只对围岩中的测试元件进行单侧布置，见图1所示。其中各土压力盒的埋设是将其受力面垂直于隧洞径向线的方式埋置，如图2所示。夯筑完毕后，盖上顶板并以混凝土浇筑块作为等效静载，在顶板上均匀施加载荷约2.3 kN，折算成土层厚度相当于1.5倍洞径的厚度。随后接通测试系统，将模型静置3 d，观察围岩应力的变化情况，待其发展稳定后，进行隧洞开挖。

图1　土压力盒布置图Fig.1 Layout drawing of soil pressure cells

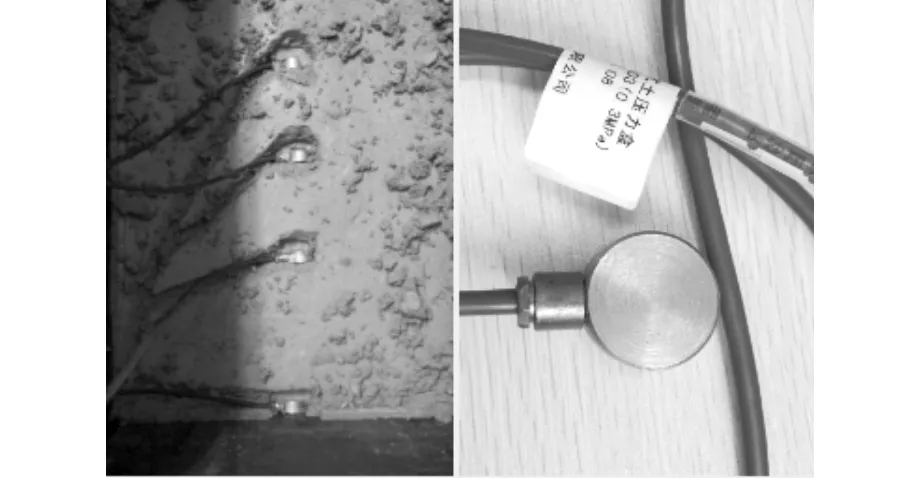
图2　土压力盒及其埋设Fig.2 Soil pressure cell and embedding

1.6隧道开挖

本模型试验的隧道设计洞径为18 cm，截面形式为圆形截面。隧洞施工采取全断面开挖方式以人工开挖的方法来进行模拟开挖过程。施工共分为20个开挖段，每段进尺2 cm，开挖行进方向为自左向右，从上午10∶20开始持续至下午12∶53完成，如图8所示。图中10∶20为开挖开始时刻，10∶49为第5开挖段结束(10 cm处)时刻，11∶35为开挖至监测断面(20 cm处)时刻，12∶14为第15开挖段结束(30 cm处)时刻，12∶53为洞室贯通时刻。此外，因膨胀土对水分的变化极为敏感[17]，在隧道贯通后，为防止围岩长时间暴露于大气中引起吸水膨胀或失水收缩而造成围岩稳定性问题，应在开挖完成后适时将衬砌施作于隧洞内，本试验在隧洞贯通后30 min开始施作衬砌。衬砌施作完毕后，采用注浆器及时注射水泥净浆将衬砌和围岩之间的间隙填充密实，以保证围岩和衬砌之间的压力正常传递，成型后的隧道模型见图3。

图3　隧道模型Fig.3 Tunnel model

2　试验结果及分析

2.1初始地应力计算

模型成型后隧道上覆土层的厚度可参考图1中的尺寸来计算，由图中可知，隧洞上覆土层的厚度应为0.61 m，但由于土量不足上部有0.12 m的厚度留余。另外，因试验要求，模型顶部有0.10 cm厚土层的压实度按原来的一半密实度进行夯筑。同时，在模型顶部均匀对称布置了2.30 kN的等效静载以折算成等量岩体厚度。

计算所需参数如下：

模型箱尺寸：l=1.1 m，b=0.4 m，土体重度γ=19.47 kN/m3

原岩厚度：

h静1=0.61 m-0.12 m-0.05 m=0.44 m

等效静载应力：

等效静载折算厚度：

上覆土层总厚度：

h=h静1+h静2=0.44 m+0.269 m=0.709 m

洞顶土层自重应力：

σ静=0.709 m×19.47 kN/m3=13.80 kPa

2.2试验结果

施工力学行为包括隧洞开挖和衬砌支护2个部分，本试验对2个部分在施工过程中围岩应力的变化数据进行了采集，并将采集到的12个测点的围岩应力值和时间的关系绘制成图4～7所示的应力—时间响应曲线，其中应力值均是由土压力盒所输出的实测值按出厂标定系数转换而得。

图4　竖向线上(隧洞下侧)各测点应力—时间响应曲线Fig.4 Stress-time response curves of each measuring points on vertical line (beneath the tunnel)

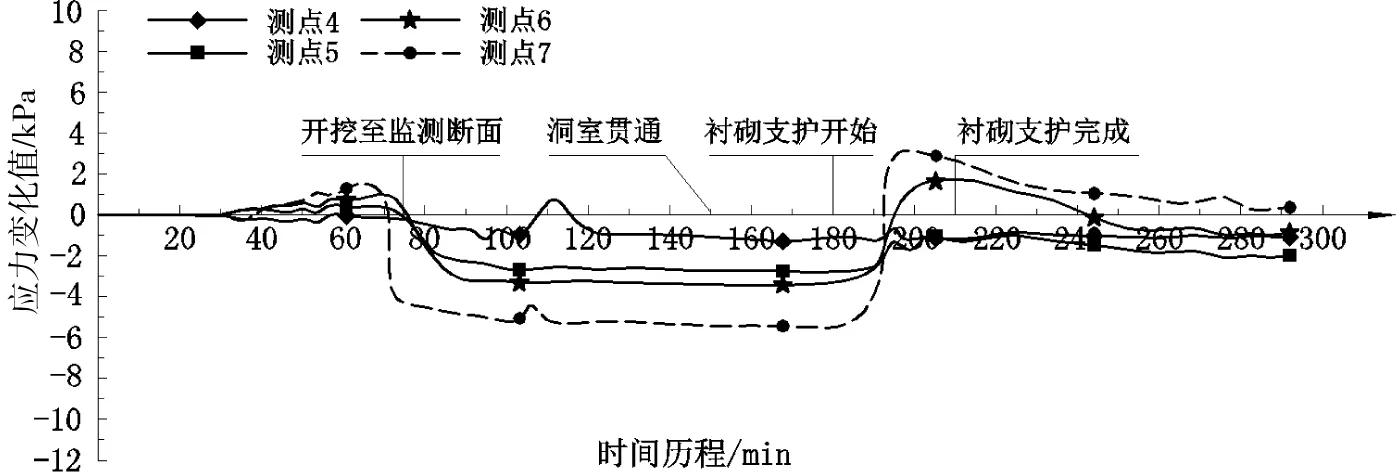
图5　水平线上各测点应力—时间响应曲线Fig.5 Stress-time response curves of each measuring points on horizontal line

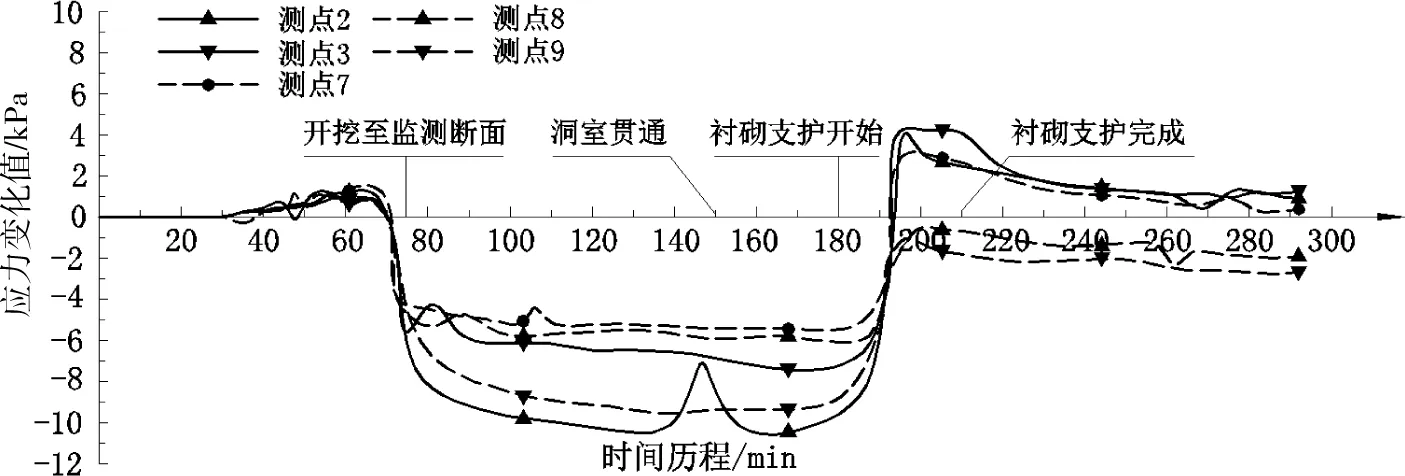
图7　洞周环向各测点应力—时间响应曲线Fig.7 Stress-time response curves of each measuring points around the tunnel

2.3试验结果分析

图7为沿洞周环向布置的各测点的应力—时间响应曲线。从图中可知，监测断面的围岩应力值，随洞室开挖面的推进及衬砌的支护而呈不同的发展变化趋势，其主要可分为洞室开挖及衬砌支护2个阶段。

洞室开挖阶段又可分为零增长、微增长、急剧下降 、缓慢减小和相对平稳5个阶段。零增长阶段表明离监测断面较远处的土体开挖对监测断面处的岩土力学行为几乎没有影响，说明隧洞开挖对前方土体的影响深度有限。该阶段大致在开挖面离监测断面5个开挖段(约10 cm)处结束，说明隧洞开挖对前方土体的力学影响深度大致在5个开挖段(约10 cm)以内。

微增长阶段反映了随开挖面的推进，开挖面前方一定区域的土体发生了荷载聚集。出现这种现象的原因主要在于监测断面后侧的土体本来处于初始地应力平衡状态，其本身承受着一定的原始土压力，而随洞室施工土体被挖出，其所承受的土压力被迫转移到周围土体上，其中大部分转移到洞周两侧土体上并向深部扩展，小部分转移到掌子面前侧未被挖去的土体上，致使出现荷载聚集现象。在各测点中，测点7的荷载聚集量最为明显，这是因为洞室两侧土体是承受上部土体荷载的主要承载部位。从图8中可知，当开挖面临近监测面时，测点7的应力释放率负增长量最大，这除了上述原因外，测点7的总应力释放量较小也是一方面原因。该阶段从第6开挖段初(10 cm处)延续到第9个开挖段末(18 cm处)结束。

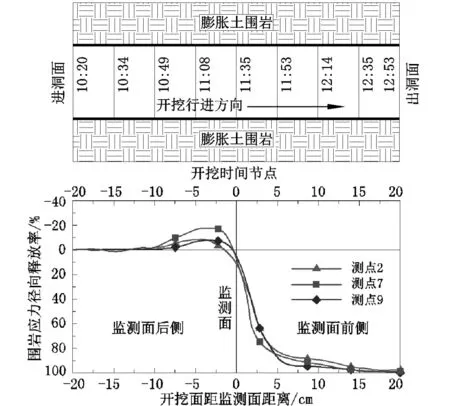
图8　洞周围岩应力释放时空效应曲线Fig.8 Space-time effect curves of stress release of wall rock around tunnel chamber

当开挖面推进到第9个开挖段初时，因监测面处的土体被挖出，围岩应力值进入急剧下降阶段或称应力主释放阶段，说明监测面处的围岩压力主要由该断面处的土体所承受，其前后两侧的土体仅能分担很小一部分。从图7～8中可知，应力急剧减小阶段主要发生在开挖面距监测面一个开挖段到通过监测面第2个开挖段末即第9～12开挖段(18～24 cm)之间，其中测点7(拱腰)处的应力释放速率最快，持续时间最短，测点2(底板)处速率最慢，持续时间最长，测点9(拱顶)处介于二者之间。

缓慢减小阶段或称应力次释放阶段，从第13开挖段初(24 cm)处至洞室贯通。在这个阶段中，随开挖面的推进，监测断面的围岩应力值呈逐渐递减趋势，其主要由开挖面离监测断面逐渐变远，所起的支撑效应越来越弱以及围岩应力重分布2部分所致。这种支撑效应主要表现在该阶段的前几个开挖段即开挖面离监测断面较近的几个开挖段，这说明监测断面前侧和后侧土体的开挖，对监测断面的围岩应力具有一定的影响，其主要表现为后侧土体的开挖对监测断面产生荷载聚集效应，前侧土体的开挖会降低土体对监测断面的支撑效应。

相对平稳阶段或称围岩应力重分布阶段，该阶段持续时间为30 min，从隧洞贯通持续到衬砌施作开始，该阶段主要体现了围岩本身具有一定的自稳能力。从各测点应力变化值来看，该值在衬砌支护前已达到相对稳定状态，说明隧洞开挖使围岩应力得到释放且洞周围岩的初始应力势能基本释放殆尽。这可以从隧洞顶部处地层应力理论值13.08 kPa以及测点9的应力—时间响应曲线中得到解释，测点9的总应力最大释放值约为10 kPa，排除静态应变测试系统的测试误差及土压力盒埋设时余坑的回填密实度的影响，此值已较为接近地层应力理论值13.08 kPa。

衬砌支护阶段可分为急剧增长和缓慢下降2个阶段。急剧增长阶段主要反映了衬砌对围岩的挤压效应。隧洞开挖的洞室直径是按照衬砌外径尺寸而确定的，在隧洞土体挖除到衬砌支护这一围岩应力重分布的过程中，围岩产生了向洞室内空的位移，使得洞室毛洞直径减小。但随衬砌被缓慢施作于洞室内，因围岩位移而减小的洞室直径又被扩大到初始洞径，此时造成围岩土体被挤压，所产是挤压效应致使应力值急剧增大；缓慢下降阶段主要反映的是由于衬砌的施作而导致围岩产生2次应力重分布，该阶段的产生是局部的，主要表现在洞周附近的围岩中。从图5及图6中距洞室边缘不同距离的各测点的响应曲线中可以看出，随距离的增大，衬砌的施作对围岩应力的影响逐渐减弱。

另外，从图4～6可知，隧洞竖直线及水平腰线上距洞室边缘不同距离布设的测点，随距离的增大，不管是隧洞开挖还是衬砌支护均对各测点围岩应力的影响逐渐减弱。这种减弱主要表现在以下几个方面：1)随距离的增大，由隧洞开挖导致的各测点的围岩应力释放量逐渐减少。由图9可知，围岩应力释放量的比率从洞周向围岩深部逐渐减小，且释放量主要表现在2倍洞径范围内，说明隧洞开挖对围岩应力的影响深度大致在2倍洞径范围以内。此外，从图5来看，测点7的应力释放值约为6 kPa，测点6约为3.5 kPa，测点5约为3 kPa，而测点4几乎不受影响，也表现出了逐级递减的规律，其中测点6的释放值较测点7大幅减少，这主要是因为在洞室土体被挖除后，洞室顶部土体通过压力拱将其自重应力转移至洞室两侧土体中，而这种转移过来的应力的水平分力正好能给测点6处的围岩应力释放起到一定的阻止效果，因此有效的减小了该处的应力释放。2)随距离的增大，衬砌支护对各监测点的应力影响也表现出逐渐减弱的规律，同样从图5中可知，测点7受衬砌支护影响的应力突变值约为9 kPa，测点6约为5.5 kPa，测点5约为1 kPa，而最远的测点4无任何影响。3)洞周围岩受洞室开挖和衬砌支护影响的岩土力学响应及行为表现最为敏捷，越往围岩深处的测点，其相应的力学响应及行为表现呈现出不同程度的迟滞效应。这从图5中可知，受洞室开挖的影响，测点7最先进入应力急剧下降阶段，随后测点6及测点5才依次出现相应的力学响应。而受衬砌支护的影响，测点7也最先进入应力急剧增长阶段，随后测点6和测点5依次进入该阶段。4)洞室开挖导致各测点围岩应力释放速率不同，且释放的持续时间也不同。其主要表现为洞周围岩应力释放速率较快，而随深度的增加，其应力释放速率逐渐减缓。从图4～6中均可以看到，洞周各测点的响应曲线中急剧下降阶段的斜率最大，越往围岩深部这种斜率越小。从图7～8中可知，洞周各测点的应力一般在15 min之内(2～3个开挖段内)释放80%，而图4～6中诸如测点1，测点5，测点6，测点10和测点11等测点的应力释放的持续时间都表现出不同程度的延长现象。5)隧洞上部各测点的围岩应力受衬砌施作的影响稍小。其原因在于上部围岩在隧洞土体开挖后产生了向洞室内空方向的较为明显的位移，此位移一般包括2部分即因土体的固结而产生的回弹位移以及在重力场作用下土体自重而引起的竖向位移。由于这种位移相对较大，且影响范围较广，促使围岩深部的土体结构变得松弛，又因重力的作用使得衬砌支护对围岩土体产生的挤压效应难以延伸到围岩深部，因此仅表现在洞周围岩区域内，这从图6中测点9及测点10的响应曲线中可得到印证，其中测点9的围岩应力突变值为8 kPa，而测点10的仅为2 kPa。

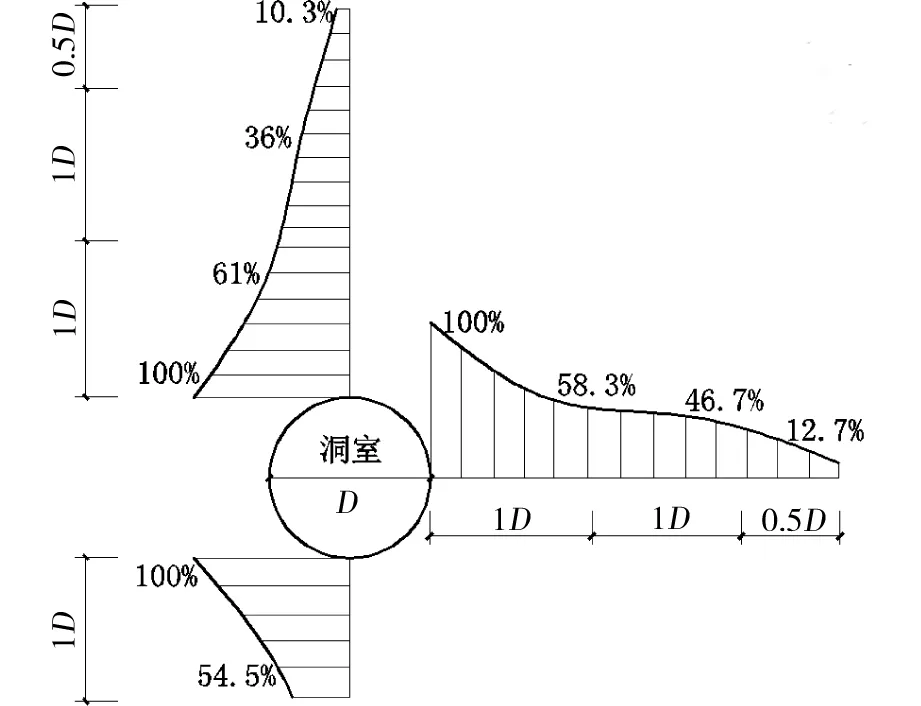
图9　不同围岩深度处的应力释放比率Fig.9 Stress release ratio of different wall rock depth

除上述规律外，沿洞周环向布置且处于不同位置的测点，所受隧洞开挖和衬砌施作的影响也不同。从图7中可以看到，由隧洞开挖而引起围岩应力急降的各测点中，测点2急降值约为9 kPa，测点3约为7 kPa，测点7约为6 kPa，测点8约为5 kPa，测点9约为8 kPa。各测点急降值不同的原因主要由2个方面组成，一方面是因各测点处的初始地层应力不同所导致；另一方面是因土压力盒按其受力面垂直于隧洞径向线方向而埋设，致使3号，7号和8号土压力盒和土体自重应力成一定的角度，使得监测到的应力值相比于2号和9号土压力盒有所折减。由衬砌支护而引起的围岩应力变化值激增的各测点中，测点2所受的影响最为明显其突变值为14 kPa，这是由于该处围岩位移量最小，仅由固结回弹位移组成，土体结构仍较为密实，受到衬砌挤压后，土体的压力传递仍较为敏感。测点7的突变值为8 kPa，该值小于测点2的突变值，其原因在于土体开挖后的围岩位移量是由土体向洞室内空固结回弹位移和因上部土体压力引起的向洞室外侧的外鼓位移两者叠合组成，因二者位移方向相反，所以减小了围岩位移量，减弱了衬砌对围岩的挤压效应，导致突变值稍小。测点9的突变值约为8 kPa，其值小于测点2的主要原因参见上述第5点所述。

3　结论

1)分析施工过程中膨胀围岩随时间及空间条件的变化而呈现出的力学响应及行为表现，得出各测点在洞室开挖和衬砌支护条件下的围岩应力—时间响应曲线，并将响应曲线的发展变化趋势按开挖和支护分为不同的阶段，其中洞室开挖过程可分为零增长、微增长、急剧下降 、缓慢减小和相对平稳5个阶段；衬砌支护过程可分为急剧增长、缓慢下降2个阶段。

2)隧洞竖向线及水平腰线上距洞室边缘不同距离的测点，其围岩应力释放量的比率从洞周向围岩深部逐渐减小，且释放量主要表现在2倍洞径范围内，说明隧洞开挖对围岩应力的影响深度大致在2倍洞径范围以内。此外，随距离的增大，围岩应力释放速率逐渐减缓，释放持续时间增长，围岩的岩土力学响应及行为表现的敏感度也逐渐减弱，且随深度的增加呈现不同程度的迟滞特性。

3)因膨胀土对水分的变化极为敏感，在今后对膨胀土隧道施工力学的研究中，可考虑不同含水率条件对隧道施工的力学响应及行为表现的影响。

[1] 关宝树. 隧道工程设计要点集[M]. 北京: 人民交通出版社, 2003.

GUAN Baoshu. Key set of tunnel engineering design[M]. Beijing: China Communication Press, 2003.

[2] 孙钧. 地下工程设计理论与实践[M]. 上海: 上海科学技术出版社, 1996.

SUN Jun. Underground engineering design theory and practice[M]. Shanghai:Shanghai Scientific and Technical Publishers,1996.

[3] 谭代明, 漆岳泰, 莫阳春. 考虑时空效应的软弱围岩隧道施工稳定性研究[J]. 水文地质工程地质, 2009,(4): 85-89,94.

TAN Daiming, QI Yuetai, MO Yangchun. Study on construction stability of soft surrounding rock tunnel considering time-space effect[J]. Hydrogrology & Engineering Geology, 2009,(4): 85-89,94.

[4] 许敬叔, 潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报, 2014,11(4): 80-84.

XU Jingshu, PAN Qiujing. Upper bound analysis of supporting pressure for shield tunnel faces[J]. Journal of Railway Science and Engineering, 2014,11(4): 80-84.

[5] 陈建勋, 王梦恕, 轩俊杰, 等. 两车道公路黄土隧道变形规律[J]. 交通运输工程学报, 2012,12(3): 9-18.

CHEN Jianxun, WANG Mengshu, XUAN Junjie, et al. Deformation rule of loess highway tunnel with two lanes[J]. Journal of Traffic and Transportation Engineering, 2012,12(3): 9-18.

[6] 扈世民, 张顶立, 郭婷, 等. 大断面黄土隧道变形特征分析[J]. 铁道学报, 2012,34(8): 117-122.

HU Shimin, ZHANG Dingli, GUO Ting, et al. Analysis on Deformation characteristics of large-section loess tunnel[J]. Journal of the China Railway Society, 2012,34(8): 117-122.

[7] 蒋树屏, 黄伦海, 宋从军. 利用相似模拟方法研究公路隧道施工力学形态[J]. 岩石力学与工程学报, 2002,21(5): 662-665.

JIANGShuping, Huang Lunhai, SONG Congjun. Physical simulation analysis on construction mechanics behavior of road tunnel [J]. Chinese Journal of Rock Mechanics and Engineering, 2002,21(5): 662-665.

[8] Hwang J H, Kikumoto M, Kishida K. Dynamic stability of multi-arch culvert tunnel using 3-DFEM[J]. Tunneling and Underground Space Technology, 2006,21: 384-389.

[9] Galli G, Grimaldi A, Leonardi A. Three-dimensional modeling of tunnel excavation and lining[J]. Computers and Geoteehnies, 2004,31(3): 171-183.

[10] 吴梦军, 张永兴, 蒋树屏, 等. 大跨扁平连拱隧道施工时空效应试验[J]. 土木建筑与环境工程, 2009,31(5): 54-58.

WU Mengjun, ZHANG Yongxing, JIANG Shuping, et al. Experimental analysis of construction time-space effect for large span and flat multi-arch tunnel[J]. Journal of Civil Architectural & Environmental Engineering, 2009,31(5): 54-58.

[11] 赵勇, 李术才, 赵岩, 等. 超大断面隧道开挖围岩荷载释放过程的模型试验研究[J]. 岩石力学与工程学报, 2012,31(增2): 3821-3830

ZHAO Yong, LI Shucai, ZHAO Yan, et al. Model test study of surrounding rock load releasing during super-large section tunnel excavation [J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(Suppl 2): 3821-3830.

[12] 王清标, 张聪, 温小康, 等. 膨胀土胀缩机理及其在控制隧道沉降中的应用[J]. 地下空间与工程学报, 2014,10(6): 1426-1432.

WANG Qingbiao, ZHANG Cong, WEN Xiaokang, et al. Application of swelling shrinkage mechanism of swelling soil in the tunnel settlement control[J]. Chinese Journal of Underground Space and Engineering, 2014,10(6): 1426-1432.

[13] Usman M，Volderauer C，Gschwandtner G，et al. Three dimensional load analysis of tunnel linings including weathering processes of the shotcrete[J]. BHM Berg-und Hüttenmännische Monatshefte, 2011, 156(12): 487-491.

[14] 万明富. 超大跨公路隧道开挖力学行为研究[D]. 沈阳: 东北大学，2009.

WAN Mingfu.Study of mechanics behavior on the super-span road tunnel construction process[D]. Shenyang: Northeastern University, 2009.

[15] JTG/T D70—2010，公路隧道设计细则[S].

JTG/T D70—2010，Guidelines for design of highway tunnel[S].

[16] 杨秀竹, 宁业辉, 雷金山, 等. 地铁隧道单个圆形溶洞地基渐进性破坏模型试验研究[J]. 铁道科学与工程学报, 2013, 10(6): 49-53.

YANG Xiuzhu, NING Yehui, LEI Jinshan, et al. Experimental study on progressive failure of subway tunnel foundation with a single cave[J]. Journal of Railway Science and Engineering, 2013,10(6): 49-53.

[17] 董新平. 铁路膨胀岩隧道施工技术研究[J]. 铁道工程学报, 2001(1):58-61.

DONG Xinping. Study on construction technology for railway tunnels with expansive surrounding rock[J]. Journal of Railway Engineering Society, 2001(1): 58-61.

Analysis on construction mechanics behavior of soil tunnelconsidering space-time effect

YANG Junping1,2,WANG Zhanyi1,LI Shengnan1,TANG Wei1

(1.Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering, Guilin University of Technology,Guilin 541004, China;2.Bureau of Housing and Urban-Rural Construction of Hezhou, Hezhou 542800, China)

Based on the physic model test of dynamic construction mechanics of expansive soil tunnel, the wall rock stress-time responsive curves of each measuring points were gained under the conditions of tunnel excavation and lining construction. According to the response curves, the mechanical response and behavioral expression of wall rock based on the changes of time and space condition during construction process are analyzed, and the developing and changing tendency of responsive curves are divided into different stages according to tunnel excavation and lining construction. The tunnel excavation process can be divided into five stages: zero increase, slight increase, dramatic decrease, slight decrease, relatively stable. Likewise, the lining construction process can also be divided into dramatic increase and slight decrease. Besides, through the analysis of measuring points with different distance from the tunnel chamber edge and local on vertical and horizontal line, it is indicated that with the increase of distance, the magnitude of wall rock stress release will reduce. At the same time release rate will drop and the sensitive of mechanical response will decrease because of tunnel excavation. Meanwhile, the impact that lead by lining construction for mechanical properties of wall rock will weaken gradually.

soil tunnel; space-time effect; stress release; springback displacement; responsive curve

2015-12-23

国家自然科学基金资助项目(51368014)

杨军平(1971-)，男，湖南永州人，副教授，博士，从事地下结构及隧道工程的研究；E-mail：529454826@qq.com

U459.2

A

1672-7029(2016)10-2009-09