基于迭代算法的多次平行泊车入位过程的研究

毕清磊季学武刘梦明朱凯

（1.重庆交通大学，重庆 400074；2.清华大学，北京 100084；3.中国农业大学，北京 100083）

基于迭代算法的多次平行泊车入位过程的研究

毕清磊1季学武2刘梦明3朱凯3

（1.重庆交通大学，重庆 400074；2.清华大学，北京 100084；3.中国农业大学，北京 100083）

为有效降低平行泊车入位过程中对车位长度的要求，对车辆多次泊车的入位状态和在车位内多次移动的运动规律进行了分析，以泊车位长度为基准构建泊车模型，利用迭代算法确定车辆出库时的车身姿态角，根据车辆参数和车位左前方障碍点的约束条件验证了出库过程的合理性。运用Matlab对一次和多次泊车入位过程进行了仿真，结果表明：在同等条件下，与一次泊车入位相比，多次泊车入位对车位长度的要求大幅降低。

主题词：路径规划迭代算法约束条件车位长度

1　前言

自动泊车过程中，由泊车辅助系统控制车辆转向，驾驶员控制车速、制动和挡位。该系统可大幅降低泊车难度，提高泊车过程的安全性，并为无人驾驶技术提供了理论基础。

目前，国内外学者已意识到自动泊车的重要性，并对其过程进行了深入的研究。文献［1］提出了基于几何学改进的最小半径法和不等半径路径规划方法，通过两种算法的结合使泊车过程得到优化。文献［2］～文献［4］通过建立闭环控制模型给出了基于路径跟踪控制器的时域尺度变换和连续曲率曲线路径规划方法的解决方案。文献［5］提出了一种基于狭窄泊车空间的最短路径多次泊车控制算法，可以很好地解决汽车平行泊车过程中遇到的问题。文献［6］利用回旋螺线将泊车路径转化为曲率连续的曲线，并用模型车验证了该路径的有效性。文献［7］提出了基于B样条理论的泊车路径规划思想，并采用非时间参考的泊车路径跟踪控制策略，最后利用快速控制原型技术对泊车功能进行了试验验证。文献［8］提出了改进的最小半径和不等半径两种路径规划方法，并通过两者的结合扩大泊车起始区域，优化整个泊车过程。文献［9］提出了最小车位模型、最短路径模型和连续曲率曲线模型三种泊车轨迹规划模型，利用veDYNA软件对三种模型进行仿真验证，证明了它们的可实现性。文献［10］对不同情况下的泊车轨迹进行研究分析，得到一种多步骤不等半径路径规划方法，试验证明，该方法对不同泊车环境具有良好的适应性。

本文在总结前人研究经验的基础上，对平行泊车过程中多次泊车的路径规划进行研究，提出一种基于迭代算法的自动泊车路径规划方法。以车位线为约束条件，以车辆在车位内的目标位置为初始位置，通过反复调整迭代车身姿态角并进行出库模拟，实现整体泊车路径规划。

2　平行泊车运动学模型分析

2.1平行泊车过程分析

自动泊车辅助系统一般采用超声波传感器或摄像头进行环境感知，通过组合仪表图像显示或声音告知驾驶员是否找到有效泊车位，然后提示驾驶员进行前进、倒车或停车操作，泊车全程由电动助力转向（EPS）系统接管转向盘，直至完成泊车或泊车失败退出系统，提示驾驶员接管转向盘。根据传感器检测到的车位长度和侧方距离，系统按照预先设定的程序进行路径规划，车位长度足够时进行一次泊车入位，车位长度不能满足一次泊车入位时，可通过车辆在车位内以最小转弯半径前后调整实现多次泊车入位。

多次泊车入位对车位长度要求更低，能适应更小的泊车空间，但其路径规划和控制算法更复杂，实现难度较大。结合目前我国基础设施不能满足日渐增多的汽车数量的现状来看，对多次泊车入位的研究更具实际意义。

2.2车辆几何模型的建立

根据车辆的整体结构和传感器安装位置，可将整车简化为如图1所示的几何模型。其中，l为车长；W为车宽；ls为轴距；lr为后悬长；B1为前轮距；B2为后轮距；h为传感器之间的距离；d为设定的安全距离；A为车前传感器检测到的预警位置；B为车后传感器检测到的预警位置；C为后轴中心；M点和N点分别为超声波传感器的安装位置。

基于可以直接获取的整车参数，可计算得到下列参数的值。

点A与点C之间的距离为：

AC与车辆纵轴线之间的夹角为：

点B与点C之间的距离为：

BC与车辆纵轴线之间的夹角为：

3　平行泊车路径规划算法

3.1一次泊车入位车位长度的计算

车辆以最小转弯半径Rmin经过一次泊车即可完全进入泊车位，并且后方超声波传感器探测预警点B与后车位线重合，车辆航向角（以前车纵轴线为基准）为0°时，相应车位长度Lonce即为一次泊车入位最小车位长度。以车位左前方障碍点E为坐标原点建立坐标系计算Lonce，如图2所示。为保证车辆顺利进入车位，需保证车辆以Rmin运动的圆心到E点的距离大于其到F点的距离，为了简化计算，设G（-ds，ds）点代替E点处的安全距离圆，其中，O点到C点的距离，即C点处的最小转弯半径。

C点到前车位线的距离为：

可得完成一次泊车所需最小车位长度为：

3.2一次泊车入位最长车位的设定

当超声波传感器检测到的车位长度L≥Lonce时即可实现一次泊车入位，随着车位长度的不断增加，不仅浪费时间而且泊车总体路径更长。因此，必须设定最大泊车位长度Lmax，当超声波传感器检测到车位长度距离L≥Lmax时，实际泊车路径规划按照车位长度Lmax设计，本文考虑到新手驾驶员对于自动泊车辅助系统的依赖性，初步设定最长车位Lmax=1.1Lonce。

3.3多次泊车车位内移动算法

当车辆在车位内移动时，本算法设定车辆起始位置为车辆在车位内的目标停车位置（车辆后方与后车位线距离为安全距离，车身外侧与前车车身外侧对齐，航向角为0°），在车位内部均以最小转弯半径进行移动，当预警位置点A和B到达车位线时为临界位置，提醒驾驶员停车换挡。根据车辆结构和参数，建立车辆简化模型如图3所示。其中，α为每一次角度迭代结束后得到的车身航向角。以停在目标位置车辆的后轴中心点C为坐标原点，建立坐标系XCY。

当车辆在预警位置点A和B停车改变运动方向时进行坐标更新迭代，如图3所示。车辆在初始位置时A点和B点的坐标分别为：

后车位线位置

前车位线位置

3.4多次泊车迭代算法

当车辆在车位内部运动时，以3.3节建立的直角坐标系进行反复迭代运算。车辆在车位内移动采用最小转弯半径，每一次迭代结束后进行坐标的更新替代和出库验证，若车辆进行出库运动时的圆心到障碍点的距离大于或等于最小转弯半径，则认为可以出库，否则继续进行迭代，直至可以出库。

3.4.1车位内迭代过程

设定初始位置为目标停车位置，航向角α为0°，开始进行车位内多次泊车迭代，迭代过程如图4所示。

3.4.2坐标的更新迭代

a.根据每一次移动后的圆心坐标与移动前圆心坐标关于移动前参考点的对称关系得到更新后的圆心坐标为：

b.若移动次数为奇数次，则向左转动转向盘向前移动，当前预警位置点A到达前车位线时停车，即xA′=xfront。车辆前进到达临界位置时如图5所示，由于车辆移动过程中转弯半径相同，圆心坐标（xO，yO）始终在Y轴上方高于yB处且保持不变，因此yB′-yO′＜0，得到

c.若移动次数为偶数次，则向右转动转向盘向后移动，当前预警位置点B到达后车位线时停车，即xB′=xback。车辆后退到达临界位置时如图6所示，由于车辆移动过程中转弯半径相同，圆心坐标（xO，yO）始终在Y轴下方低于yA处且在转弯过程中保持不变，因此yA′-yO′＞0，得到

d.偏航角发生变化后，后轴中心点C坐标更新为：

前预警位置点A坐标更新为：

后预警位置点B坐标更新为：

航向角变为：

e.完成坐标更新迭代后继续进行角度的累加，直至验证成功得到理想车身姿态角。

3.4.3出库验证

验证过程如图7所示，当进行验证是否能够安全出库时通过坐标迭代已知后轴中心点C′的坐标（xC′，yC′）和车身偏航角α的值，根据几何关系可以计算出车身轴线的直线方程为：

圆心O到后轴中心点C′的连线为最小转弯半径RC，并且与车身轴线相切，由此得到经过圆心O和后轴中心点C′的直线方程为：

又已知圆心O（xO，yO）到点C′（xC′，yC′）的距离为RC，可得

圆心O的坐标为：

已知E点坐标，可得G点坐标为：

得到OG的距离为：

3.5车位外运动轨迹分析

通过上述步骤计算出车辆成功出库的航向角后，根据第2段圆弧的转弯半径为RC，求出其圆心坐标（x2，y2）。以安全距离和RC为约束条件，求出车辆在最近倒车位置时的圆心坐标（xnear，ynear），作轨迹圆的内公切线，其与两圆心连线交点P的坐标为：

根据斜直线到圆心（xnear，ynear）距离等于RC，结合直线上P点坐标可求出斜直线方程，如图8所示。在侧方距离H一定的情况下，求出车辆能够达到的最远倒车位置处的圆心坐标（xfar，yfar）和半径Rmax，可得本方案为保证乘坐舒适性（非最小转弯半径）而采用的第1段圆弧的半径为：

分别求出各关键点的坐标，即可进行自动泊车试验，完成路径规划算法的设计。

4　仿真计算与分析

采用本田某型号车为实车验证车辆，通过技术手册获取车辆的部分整车参数如表2所示，为防止车辆在行驶过程中EPS助力电机长时间处于堵转的高负荷状态，一般根据助力电机的功率设定转向盘最大转角，该数据无法从技术手册中获取，因此本文通过测力转向盘获得，测得数据如图9所示。

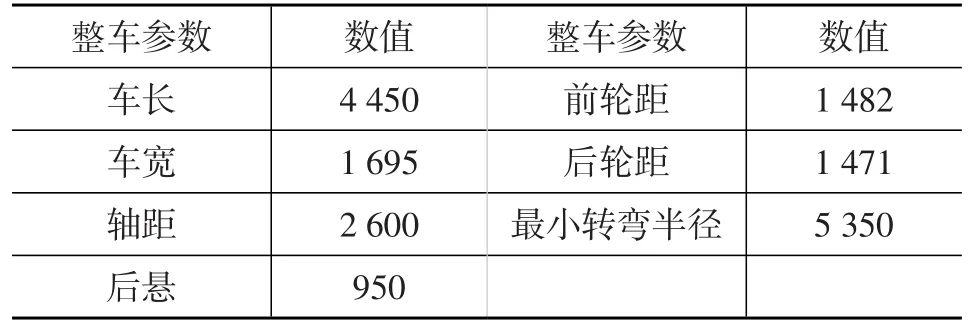
表2　试验车辆整车参数　mm

由图9可知，该车辆转向盘顺时针转动和逆时针转动最大转角略有差异，转向盘最大转角范围在580°～ 600°之间，本方案限制转向盘最大转角为535°，取安全距离d=250 mm，最大泊车位长度Lmax=1.1Lonce。利用Matlab进行仿真试验，得到一次泊车入位和多次泊车入位的仿真结果如图10所示。

由图10可以看出，当取侧方距离H=1 000 mm保持不变时，能够进行一次泊车入位需要的最小车位长度Lonce=6 556 mm，由此得到限制的最大泊车位长度Lmax=7 211.6 mm，随着车位长度逐渐缩短，入位车身姿态角不断增大，限定前后移动次数最多为5次时，能够通过多次泊车实现入位要求的最小车位长度为5 421 mm。

5　结束语

以车辆在车位内的运动规律为依据，在充分考虑EPS助力电机的负荷和驾驶员泊车过程中的舒适性的基础上，运用逆向思维提出一种基于角度迭代算法的自动泊车路径规划方法。仿真结果表明：当车位长度足够时，可实现一次泊车入位；当车位长度不足时，考虑工程实现问题，泊车次数限定为最多5次，运用多次泊车可实现泊车入位的最小车位长度不大于车身长度加1 m泊车空间，接近于大众高端车型泊车辅助系统最小车位长度不小于车身长度加800 mm泊车空间的要求［11］，证明了该方法的有效性和实用性。

1Wang D，Liang H，Mei T，et al.Research on self-parking path planning algorithms.IEEE International Conference on Vehicular Electronics and Safety，Beijing，2011.

2Emese Szádeczky-Kardoss，Bálint Kiss.Path Planning and Tracking Control for an Automatic Parking Assist System.European Robotics Symposium，Prague，2008.

3Vorobieva H，Minoiu-Enache N，Glaser S，et al.Geometric Continuous-Curvature Path Planning for Automatic Parallel Parking.IEEE International Conference on Networking，Sensing and Control，Evry，2013.

4Kim J M，Lim K I，Kim J H.Auto Parking Path Planning System Using Modified Reeds-Shepp Curve Algorithm.International Conference on Ubiquitous Robots and Ambient Intelligence，Kuala Lumpur，2014.

5Lv Z，Zhao L，Liu Z.A path-planning algorithm for parallel automatic parking.Third International Conference on Instrumentation and Measurement，Computer，Communication and Control，Shenyang，2013.

6Vorobieva H，Glaser S，Enache N M，et al.Automatic Parallel Parking in Tiny Spots：Path Planning and Control.IEEE Transactions on Intelligent Transportation Systems，2015，16（1）：396～410.

7李红.自动泊车系统路径规划与跟踪控制研究：［学位论文］.长沙：湖南大学，2014.

8王道斌，梁华为，杨妮娜，等.两种自动泊车路径规划方法的对比研究.电子测量技术，2011，34（1）：27～38.

9吕镇基.自动泊车轨迹规划算法研究及视觉平台结构设计：［学位论文］.哈尔滨：哈尔滨工业大学，2012.

10王芳成.自动平行泊车系统的研究：［学位论文］.合肥：中国科学技术大学，2010.

11大众集团.智能泊车辅助系统［EB/OL］.http://www.xietui.com/manual/96/168，2013-12-27.

（责任编辑斛畔）

修改稿收到日期为2016年7月1日。

Research of Parking Process of Multiple Parallel Parking Based on Iterative Algorithm

Bi Qinglei1，Ji Xuewu2，Liu Mengming3，Zhu Kai3
（1.Chongqing Jiaotong University，Chongqing 400074；2.Tsinghua University，Beijing 100084；3.China Agricultural University，Beijing 100083）

In order to reduce demand for parking space length in the process of parallel parking，in this paper，the vehicle's status of multiple parking in place and the motion law of multiple movements in parking space are analyzed.A parking model is built based on the parking space length，the attitude angle of vehicles driving out of place is determined through iterative algorithm，and the rationality of the process vehicle driving out of place is verified according to vehicle parameters and constraint conditions of front left obstacle point of parking space.Single and multiple parking in place are simulated with Matlab，the result shows that：compared with single parking in place，the demand of parking space length is reduced greatly in multiple parking in place in the same conditions.

Path planning，Iterative algorithm，Constraint conditions，Parking space length

U471.1；TP273

A

1000-3703（2016）10-0011-05