十次对称二维准晶悬臂梁弯曲问题

武亚楠，李联和，2

（1.内蒙古师范大学　数学科学学院，内蒙古　呼和浩特　010022；2.内蒙古自治区纳米材料与技术重点实验室，内蒙古　呼和浩特　010021）

十次对称二维准晶悬臂梁弯曲问题

武亚楠1，李联和1，2

（1.内蒙古师范大学数学科学学院，内蒙古呼和浩特010022；2.内蒙古自治区纳米材料与技术重点实验室，内蒙古呼和浩特010021）

本文基于十次对称二维准晶平面弹性问题的最终控制方程，发展了在自由端受集中力作用下悬臂梁弯曲问题的逆解法.通过引入满足基本方程的试探应力函数，结合声子场和相位子场的应力边界条件，获得了声子场和相位子场位移的解析表达式.讨论了施加载荷对声子场与相位子场位移的影响.

准晶；悬臂梁；逆解法；试探函数

1　引言

1984年Shechtman等［1］从实验上发现了一类即区别于晶体又区别于非晶体的固体材料——准晶.2009年准晶的研究取得了突破性的进展［2］，科学家在自然界中发现了准晶.准晶的发现改变了凝聚态物理把固体划分成晶体和非晶体的传统概念，揭示了一种新的对称性准周期对称性的存在，极大的深化了人们对晶体学和凝聚态物理的认识.

由于准晶结构的复杂性，使其弹性理论的研究存在着较大的困难.研究者们成功发展了群理论［3］、积分变换法［4，5］、格林函数法［6，7］、复变函数法［8-10］及Stroh公式［11］等方法研究准晶的弹性和缺陷问题.

在工程应用中，梁结构被大量地使用，长期以来，许多学者对梁的理论进行了大量研究.然而到目前为止，关于准晶材料梁理论的研究较少.文献［12-14］给出了一维、二维准晶梁平面问题的控制方程和基本解，为进一步研究准晶梁理论奠定了基础.

本文采用逆解法研究了十次对称二维准晶悬臂梁弯曲问题，有效地避免了直接求解复杂的准晶弹性理论偏微分方程边值问题.先给出准晶悬臂梁的试探应力函数，然后根据本构关系、边界条件等求出其位移表达式，并讨论了在集中力作用下声子场和相位子场位移变化的规律.

2　基本方程

若考虑三维弹性准晶结构在z轴方向的尺寸较其它两个方向小得多，力全部作用在x-y平面内且不沿z轴方向变化，此时问题可以简化为x-y平面内的平面应力问题.

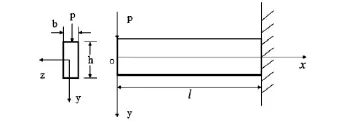
图1　准晶悬臂梁

考虑如图1所示的对称二维准晶悬臂梁［15］.假设z轴为二维十次对称准晶周期方向，x-y平面为准周期平面，悬臂梁长l、高h、厚b，其厚度远小于长度及高度，自由端受x-y平面内的集中力的作用，不计体力.

根据准晶弹性理论［3］，我们有变形几何方程

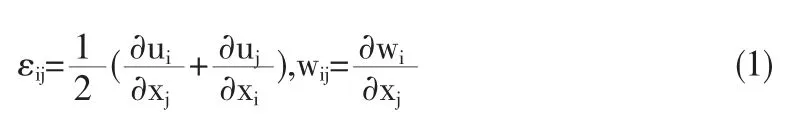
平衡方程（体力忽略的情况）

和广义胡克定律

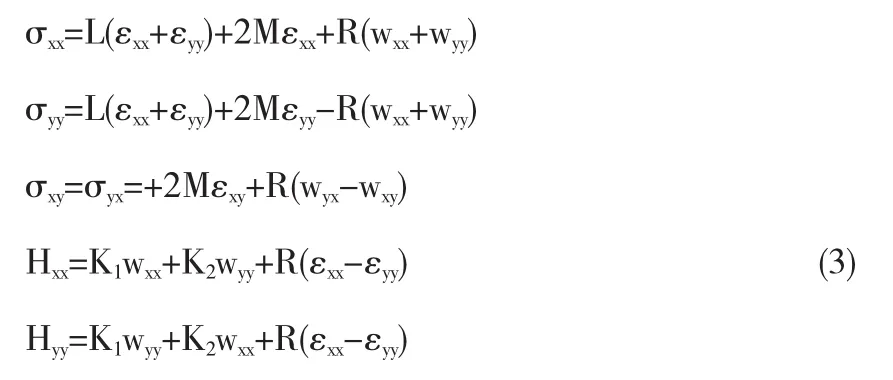
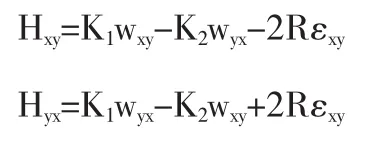
其中

为声子场弹性常数.方程（1）和（2）采用了张量记号.εij和wij表示声子场和相位子场的应变分量，ui和wi表示声子场和相位子场位移分量，σij和Hij表示声子场和相位子场应力分量，Cijkl，Kijkl和Rijkl分别表示声子场、相位子场和声子场和相位子场耦合弹性常数.

由变形几何方程（1），可得变形协调方程：

3　十次对称二维准晶悬臂梁受集中力下的解析解

如果我们引入应力势ø（x，y），ψ1（x，y），ψ2（x，y）如下

那么平衡方程（2）将自动满足.根据广义胡克定律（3），可得到用应力分量表示的所有的应变分量.引入新的应力势函数G如下

其中

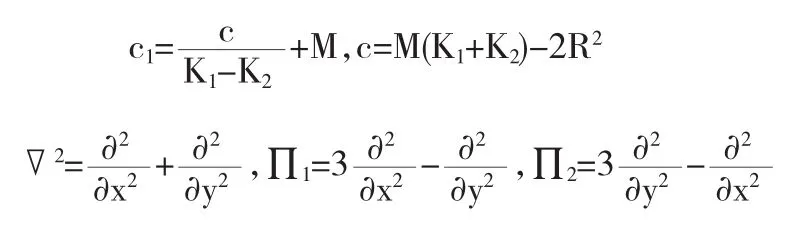
并且应力势函数满足四重调和方程

那么方程组（1）-（3）将自动满足，即十次对称二维准晶平面弹性问题的最终控制方程是一个四重调和方程.

针对本文考虑的悬臂梁问题，我们取满足最终控制方程（8）的试探函数为

那么由方程（7）可得

根据圣维南原理，准晶悬臂梁放松的边界条件为：

将方程（11）-（13）代入到（6）中得到相应的应变函数，分别对应变函数εxx和εyy积分可以得到：

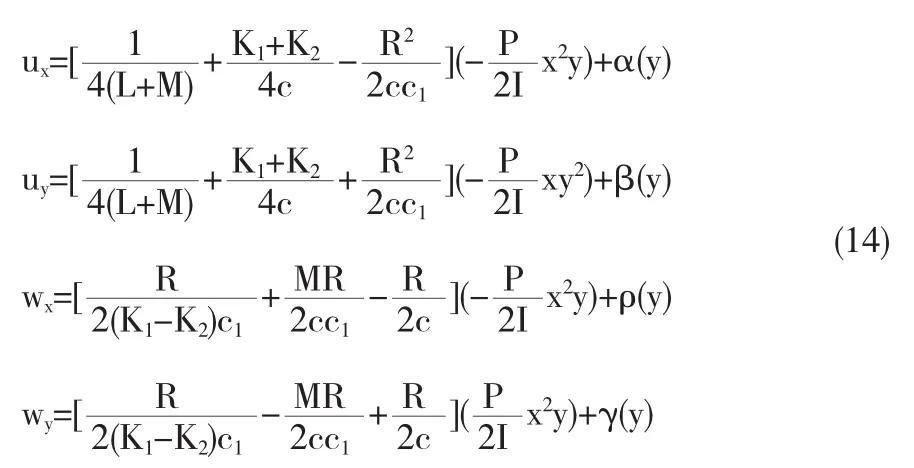
用位移来表示的应变εxy与用应力来表示的应变εxy的两个表达式令其相等并移项整理得

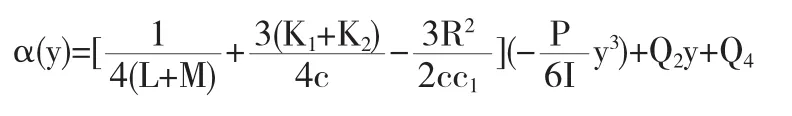
这里Q3、Q4均为常数.将β（x），α（y）代入方程（15），根据边界条件：x=l，y=0，ux=uy=0，解得

同理能够得到相位子场用应力表示的应变和用位移来表示的应变，用应力表示的应变wxy、wyx的和与位移来表示的应变wxy、wyx的和相等并移项整理得：

这里E1，E2，E3，E4均为常数.将γ（x），ρ（y）代入方程，根据相位子场边界条件：解得

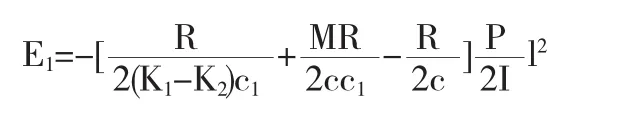
图2　ux随y的变化趋势

图3　uy随y的变化趋势

图4　wx随y的变化趋势

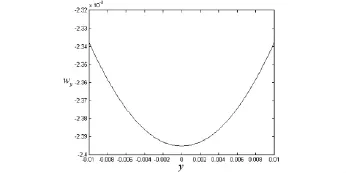
图5　wy随y的变化趋势

4　算例

为了检验以上表达式，用Matlab软件画图，图2-5分别给出处的位移ux、uy、wx和wy随y坐标轴的变化规律.

其中的常数为：

C11=23.432GPa，C12=5.741GPa，K1=12.2GPa

K2=2.4GPa，R=-0.11GPa，P=2×106Pa，l=0.5m，

h=0.05m，b=0.005m

由Matlab所绘制的声子场和相位子场位移随y的变化趋势，我们能够看出：

〔1〕Shechtman D，Blech I，Gratias D，Cahn J W.Metallic phase with long-range orientational order and no translational symmetry［J］.Phys Rev Lett，1984，53：1951-1953.

〔2〕Bindi L，Steinhardt P J，Yao N.Natural Quasicrystals［J］.Science，2009，324：1306-1309.

〔3〕Hu C Z，Wang R H，Ding D H.Symmetry groups physicalproperty tensors，elastricity and disolcationsin quasicrystals［J］.Rep Prog Phys.2000 63（1）：1-39.

〔4〕范天佑.固体与软物质准晶数学弹性与相关理论及应用［M］.北京：北京理工大学出版社，2014.

〔5〕Li X F，Fan T Y.New method for solving elasticity problems of some planar quasicrystals and solutions［J］.Chin.Phys.Letter，1998，15（4）：278-280.

〔6〕J Bachteler，H.R.Trebin，Elastic Green’s function of icosahedral quasicrystals［J］.Eur Phys J.1998，B4：299-306.

〔7〕Gao Y and Ricoeur A.Green’s functions for infinite bi-material planes of cubic quasicrystals with imperfect interface［J］.Phys Lett A，374（42）：4354-4358.

〔8〕Li L H，Fan T Y.Stress potential function formulation and complex variable function method for solving the elasticity of quasicrystals of point group 10 and the exact solution for the notch Problem［J］.J Phys Condensed Matter.2006，18：10631-10641.

〔9〕李联和，刘官厅.一维六方准晶中螺形位错与楔形裂纹的相互作用［J］.物理学报，2012，62（8）：086103-1-086103-5.

〔10〕Li Wu，Fan T Y.Plastic analysis of crack problem of two-dimensional decagonal Al-Ni-Coquasicrystalline materials of point group 10［J］.Chin Phys B，2011，20：036101-036109.

〔11〕E.Radi，P.M.Mariano，Stationary straight cracks in quasicrystals［J］.Int.J.Fract.2010，166：105-120.

〔12〕Gao Y.The exact theory of one-dimensional quasicrystal deep beams［J］.Acta Mechanica，2010，212（3-4）：283-292.

〔13〕Gao Y，Yu L Y，Yang L Z and Zhang L L.The refined theory of 2D quasicrystal deep beams based on elasticity of quasicrystals［J］.Struc Eng Mech，2015，53（3）：411-427.

〔14〕Li XY.Elastic field in an infinite medium of one-dimensional hexagonal quasicrystal with a planar crack［J］.Int J Solids and Struct.2014，51：1442-1455.

〔15〕朱纯章.悬臂压电梁自由端受集中力的解析解［J］.南京工程学院报，2001，1（1）：12-15.

O346.1

A

1673-260X（2016）10-0001-04

2016-06-13

国家自然科学基金（11462020，11262107，11262012）；内蒙古自然科学基金（2015JQ01，2015MS0129）和内蒙古青年科技英才项目（NJYT-13-B07）资助的课题