圆锥曲线易错题剖析

◇　江苏　冯　平



圆锥曲线易错题剖析

◇江苏冯平

圆锥曲线问题的求解中常因审题不严、考虑不周、不能挖掘出题目的隐含条件等，造成对有关概念的理解上出现偏差或是错误，使解题陷入困难或产生错误．下面对易错点进行剖析，以引起同学们的注意.

1　没有重视“斜率是否存在”的问题

在解题中,很多学生没有考虑斜率是否存在的问题,由此出现了解题错误的情况．

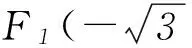
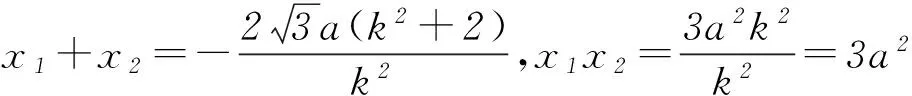
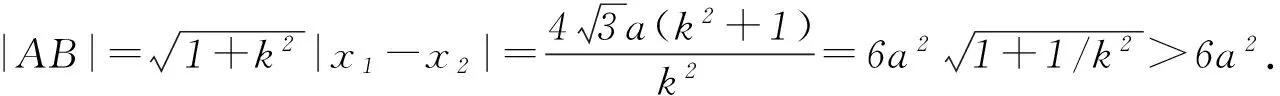
剖析学生在解题过程中没有注意到过原点斜率不存在的直线,因此造成了解题失误．

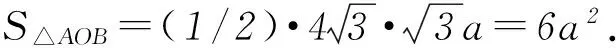
2　没有考虑到二次曲线的性质

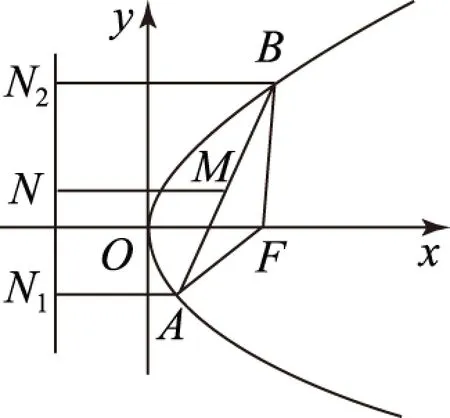
图1

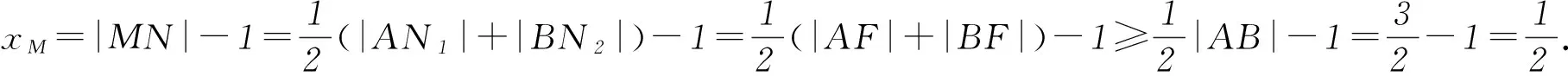
剖析由于抛物线y2=4x的通径长度为4,因此任意过抛物线焦点F的弦长都不会小于4．在题目中,弦|AB|的长为3,因此|AF|不经过抛物线y2=4x的焦点F,此时需要考虑AB与对称轴x垂直的情况.当弦AB垂直于x轴时,将|y|=3/2代入y2=4x,得到点M的横坐标为xM=9/16,因此AB的中点M到y轴的最小距离为9/16．在解题的过程中,应当按照题目给出的条件联系相关知识点,学会分辨有利条件,才能够提高解题效率．

3　没有灵活的运用相关知识

在解题中,有很多学生对于数学知识理解不透彻,无法灵活运用相关知识,导致解题失误．

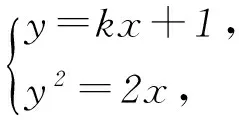
剖析上述解法共出现了3处错误: 1)在假设所求直线的方程为y=kx+1时,未考虑k=0与斜率不存在的情况．2)直线与抛物线仅有一个交点,此时有相交与相切2种情况．但在上述解题方法中,并未想到相交的情况,仅考虑了相切的情况．出现此种情况,是因为学生没有深入思考直线与抛物线“相切”与“仅有1个交点”的关系,理解不透彻．3)将直线方程与抛物线方程联立后,就可得到一元二次方程,需要考虑到判断式,二次项的次数不可能是零,即k≠0．

综上所述,在教学中,教师可结合学生平时的训练题,紧扣教材,使用实际案例来帮助学生分析易错题．由此引导学生更好的完善解题方法与解题思路,培养学生的思维能力．

江苏省金湖中学)