浅谈数与形的转化在函数最值中的应用

◇　江苏　孙文腾



浅谈数与形的转化在函数最值中的应用

◇江苏孙文腾

著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休．” 数形转化是数学解题中至关重要的思想方法,巧用数形转化思想妙解数学问题,往往可以化抽象为具体,化复杂为简单．本文笔者结合具体教学实例,对数形转化在函数最值中的应用进行分析,以供参考借鉴．

1　化最值为距离

函数最值问题是函数教学要突破的重、难点内容．巧妙地运用数形转化思想将函数最值问题转化距离问题,往往可以简化解题过程,使问题得以快速、有效获解．通常情况下,形如(x-a)2+(y-b)2的函数最值问题,往往可以转化成动点到定点距离平方的最值问题．

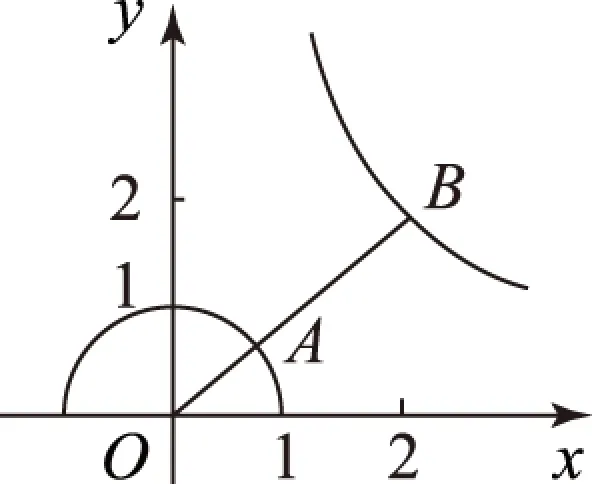
图1

2　化最值为斜率

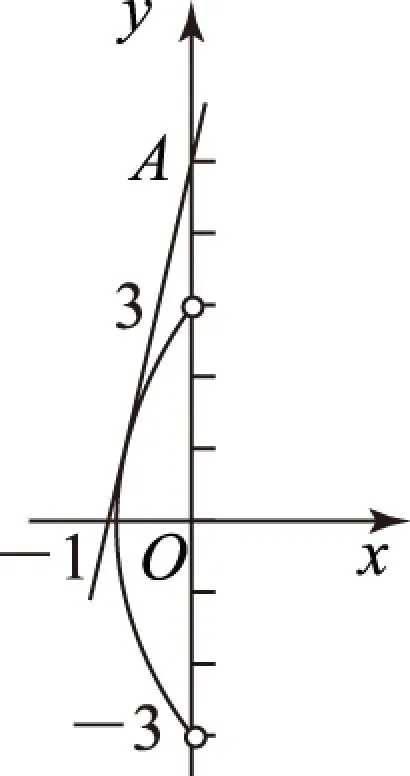
图2

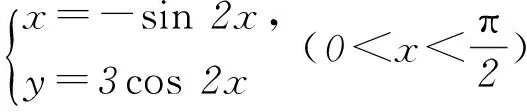
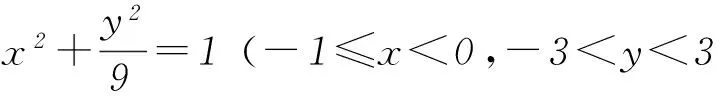
过A作直线y=kx+5代入上式,由相切(Δ=0)可求出k=4,由图2可知k的最小值是4,故选项B正确．

3　化最值为截距

一般地,当函数最值问题以t=ax+by形式出现,则可以将函数最值问题转化为动直线截距的最值问题,借助几何意义画出图形,这样往往可以化繁为简,使问题迎刃而解．

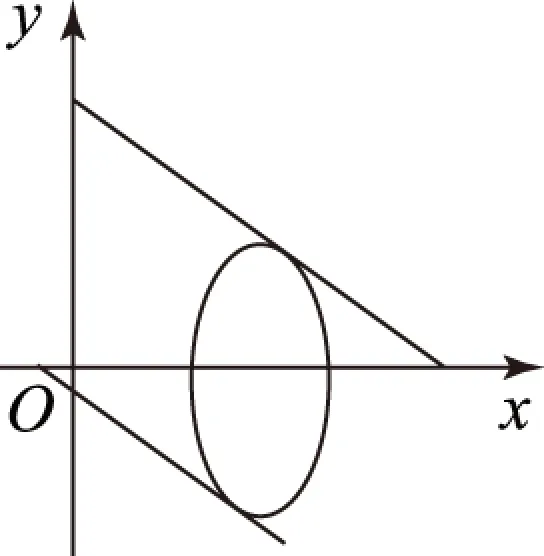
图3

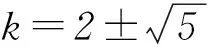
总之,数与形作为数学研究的基本对象,在一定条件下可以相互转化．在平时数学教学中,教师要注意数形结合思想的有效渗透,根据数与形的对应关系,将数与形进行相互转化,巧妙结合,通过以形助数、以数解形,使代数问题几何化,几何问题代数化,从而使问题顺利求解．

江苏省建湖高级中学)