运用数学思想，巧解集合试题

◇　江苏　司春炎



运用数学思想，巧解集合试题

◇江苏司春炎

集合在高考中虽然一般定位于基础试题,但近年来对集合知识的考查题型也常出现灵活、新颖的创新题．对于此内容的教学,最重要的就是渗透数学思想,帮助学生积累解题技巧,常见的数学思想包括数形结合、化归转化、分类讨论等,本文将深入挖掘集合试题中的数学思想,希望对学生解决集合试题能力的改善和提高有所帮助．

1　数形结合思想

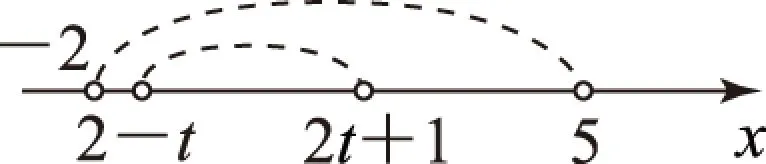
图1

首先,由M∩N=N可知N⊆M．此时,集合M已知,而集合N含有参数t．欲使N⊆M成立,存在2种情况,即N为∅和N不是∅．当N为∅时,N⊆M成立,即2t+1≤2-t,解出t≤1/3．当N不是∅时,我们不妨要求学生利用数形结合的思想进行求解．要使集合M、N满足要求,结合图1可知2-t<2t+1、2t+1≤5、2-t≥-2,解得1/3

2　化归转化思想

Aτ={φ,{a},{c},{a,b,c}};

Bτ={φ,{b},{c},{b,c},{a,b,c}};

Cτ={φ,{a},{a,b},{a,c}};

Dτ={φ,{a,c},{c},{b,c},{a,b,c}}

3　分类讨论思想

1) 当p=2时,得原方程为2x2-4x+2=0,集合B={1}是集合A的子集．

2) 当p=4时,得原方程为2x2-8x+8=0,集合B={2}是集合A的子集．

3) 当p<2或p>4时,Δ<0,集合B为空集,是集合A的子集．

4) 当2

综上可知,实数p的取值范围是p∈(-∞,2]∪{3}∪[4,+∞)．

总之,数学思想是解决集合问题的有效工具．当然,对学生数学思想的培养不会一蹴而就,我们必须在日常教学与习题训练中积极渗透,不断创新,从而有效提高学生的解题能力．

江苏省平潮高级中学)