高中数学三角函数的教学策略探讨

◇　山东　李真真



高中数学三角函数的教学策略探讨

◇山东李真真

三角函数公式众多、内容丰富、方法灵活,可有效考查学生学习效果、分析问题和解决问题的能力．本文笔者综合分析目前大多数高中学生在三角函数版块学习上遇到的困难,并就三角函数解题方面提供若干参考建议,以期为创新教学策略带来新的启发．

1　三角函数教学常见问题

1)概念记忆困难．尽管高中生已经具备三角函数学习基础,但大多数学生尚未对三角函数这一概念有一个准确、全面的认识,多是一知半解,不能灵活运用诱导公式、转换公式．

2)公式推理困难．一项相关调查发现,约有67.3%的高中学生不能灵活运用三角函数的正弦定理、余弦定理以及一系列诱导公式等,公式推理存在一定的困难．

3)综合运用能力较差．很多学生难以判断何时该应用三角函数求解,尤其是对部分隐性函数问题反应不够灵敏．

2　三角函数教学策略

2.1强化学生对基本公式概念的理解

数学基本概念是对数学本质与数学基本特征的集中反映．因此,教师应该创新教学模式,注重培养学生理解数学概念的能力,引导学生发散思维．一般情况下,高一阶段会安排三角函数知识学习,由于学生初步接触几何图形,因而较三角函数,学生更容易理解和掌握几何图形知识．对此,教师应该以强大的多媒体技术为支撑,将枯燥无味的三角函数以直观、生动的形式展现在学生面前,理清学生思维,突出重难点,使学生更好地理解所学知识．

2.2在整个数学教学体系中融入三角函数

新课改要求数学教学应该遵循“循序渐进”原则,通过螺旋上升方式让学生由浅入深、有顺序、有层次地理解和掌握数学知识,增强知识之间的脉络关联,构建成一张系统、完整的知识网,以方便学生记忆．因此,教师在开展课堂教学时,应该有效拓展三角函数版块内容的教学空间,保证教学实践在设定好的框架内有序地进行．同时,教师也应该对三角函数与非三角函数之间的关系有一个充分的认识,引导学生更好地掌握三角函数知识,并提高学生解题能力．

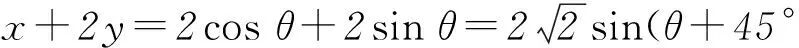
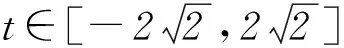
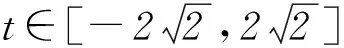
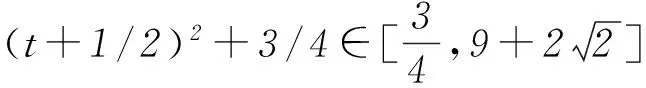
条件的形式使代入消元出现困难，如果从平方和等于1的特点联想到三角函数的性质，那么就可以采用三角换元，将目标函数转化为三角函数，从而问题迎刃而解.

2.3注重锻炼学生逻辑思维能力和推理能力

学生在求解三角函数有关问题时,应该注意从“函数名称”“角”等角度分析题目的特征和结构,找准解题方法,避免盲目解题．

大多数学生解答此题时有以下3种思维:

1) 由tanα=3>0知α在第一象限或第三象限,据此求出sinα和cosα的值,进而得出问题答案．

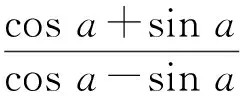
3) 对所求式进行转化,即得出

显然,后2种方法较第1种方法更便捷．

2.4加强培养学生反省抽象与综合性思维能力

要掌握高中数学三角函数版块的内容,需要学生具备较强的逻辑思维和抽象思维能力．因此,教师在开展教学过程中,不仅要强化学生的理论知识,还要注重培养学生的思维发散和思维创新能力．教师在提出一个中心问题后,鼓励学生积极发散思维,全方位、多角度地进行思考,让思维的触角延伸到问题的每一个关节,这样不仅利于加深学生对知识的理解和记忆,更有利于提高学生独立思考能力、独立解题能力,并在思考过程中实现思维创新．

山东省济南市长清中学)