辅助函数法在高中数学解题中的应用

◇　天津　明廷军



辅助函数法在高中数学解题中的应用

◇天津明廷军

“构造辅助函数”是一种重要的思想方法,在数学中具有非常广泛的应用.辅助函数不出现在条件和结论中,它是在解题的过程中被解题者构造出来的,类似于初中平面几何中的辅助线,起辅助解题的作用.在高中数学学习中如果能借鉴“构造辅助函数”的思想,很多数学问题都能轻松破解.

本文从“辅助函数”在命题、不等式、方程、最值、代数求值5个方面的应用来介绍辅助函数法.

1　在命题中的应用

A充分不必要条件;

B必要不充分条件;

C充要条件;

D既不充分又不必要条件

分析本题如果从充分条件、必要条件的定义出发,对a、b的正负进行分类,可以得出结论,但是过程较为烦琐.如果注意到a|a|>b|b|两边的结构类似,我们就可以考虑构造函数f(x)=x|x|.

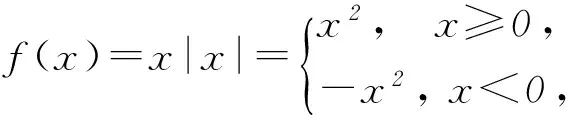
因为a|a|>b|b|⟺f(a)>f(b),所以a>b⟺f(a)>f(b).

2　在不等式中的应用

A(-∞,0];B(0,1);

C(-∞,1];D[1,+∞)

分析对于抽象不等式,由于不知道解析式,要想转化成具体不等式较为困难,所以可以考虑构造出一个新的函数,利用单调性来解决问题.

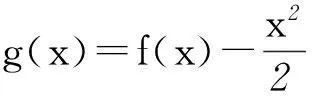
又因为g′(x)=f′(x)-x>0,所以g(x)在(0,+∞)上单调递增,由奇函数的性质可知g(x)在R上单调递增.

因为f(2-a)-f(a)≥2-2a,

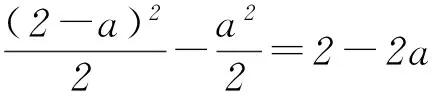
所以

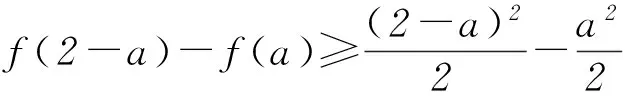
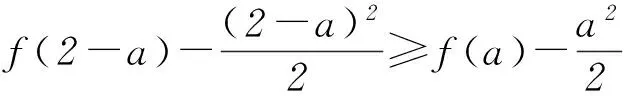
所以g(2-a)≥g(a), 2-a≥a,所以a≤1.

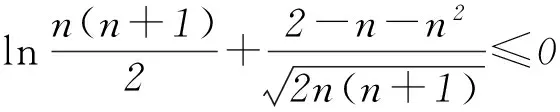
分析这个不等式中的一个基本元是n(n+1),为了更加简化问题,我们把不等式进一步变形为

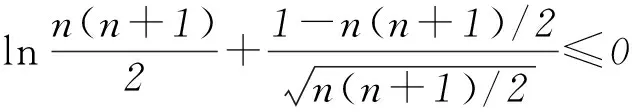
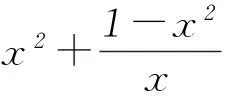
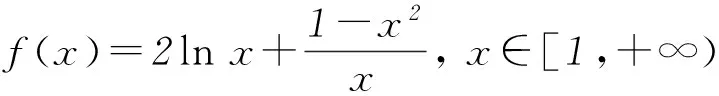
(1+m)n<(1+n)m.

分析(1+m)n<(1+n)m⟸

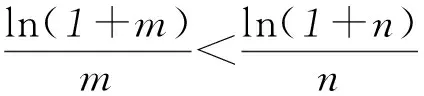
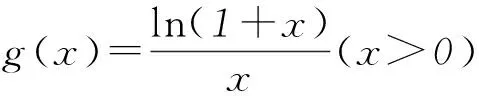
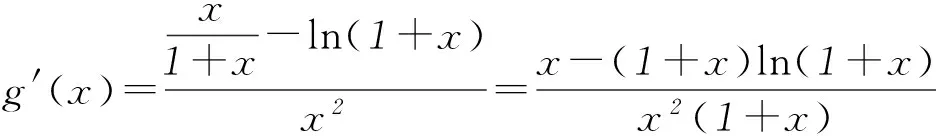
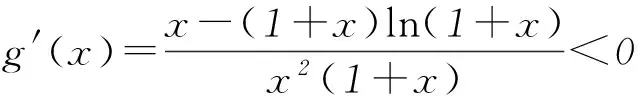
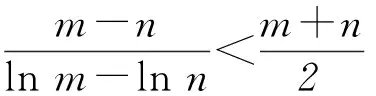
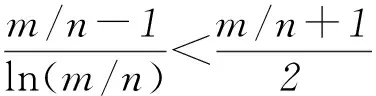
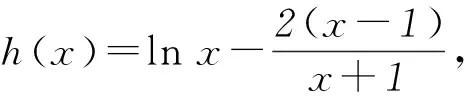
3　在解方程中的应用

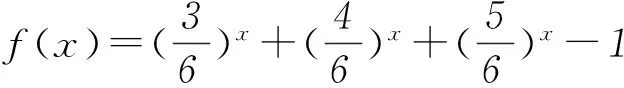
4　在求最值中的应用

分析求e的最大值可尝试建立e的不等关系.

解构造以x为自变量的二次函数:

y=4x2+2(a+b+c+d)x+(a2+b2+c2+d2),

①

即y=(x+a)2+(x+b)2+(x+c)2+(x+d)2.式①的值恒为非负数,则其判别式小于或等于0,即

Δ=4(a+b+c+d)2-4×4×(a2+b2+c2+d2)≤0,

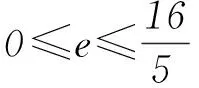
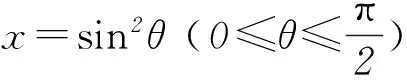
5　在代数求值中的应用

分析此题若用常规方法,分别求出x和y的值后再求x+y，既繁又难,若从2个方程的结构特点出发,构造辅助函数f(t)=t3+1 997t,可以很快求出答案.

解令f(t)=t3+1 997t,则f(t)是定义在R上的奇函数,且f(t)在R上单调递增.因为f(x-1)=-1,f(y-1)=1，所以f(x-1)=-f(y-1)，所以x-1=-(y-1),即x+y=2.

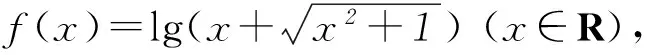
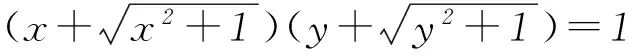
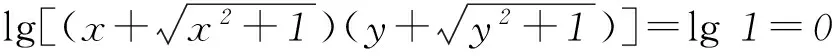
所以f(x)=-f(y),即f(x)=f(-y).

又因为f(x)是定义在R上的增函数，所以x=-y， 即x+y=0.

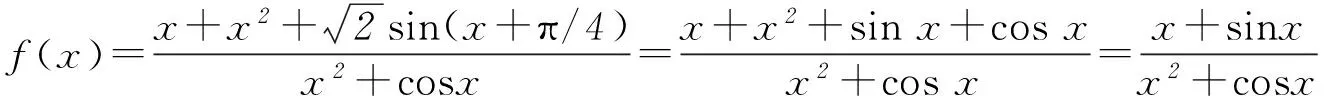
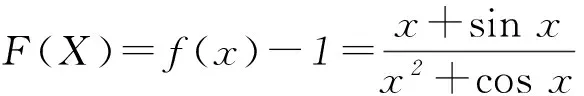
因为奇函数图象关于原点对称,所以

Fmin(X)+Fmax(X)=0.

因为Fmax(X)=fmax(x)-1=M-1,Fmin(X)=fmin(x)-1=m-1,所以(M-1)+(m-1)=0，所以M+m=2.

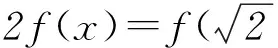
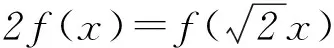
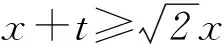
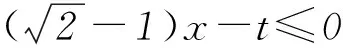
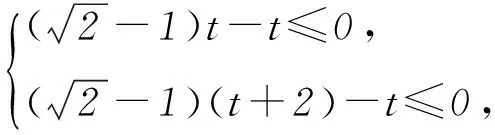
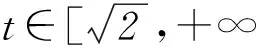
在求解某些数学问题时,避开问题本身,通过发现条件中的“基本元”或结构特点来构造一种新的函数关系,使问题在新的视角下转化,并利用函数的单调性与奇偶性来解决问题,是一种很有效的解题方法.

天津市耀华中学)