结合整体思想，突破数学难题瓶颈

◇　甘肃　张　瑛



结合整体思想，突破数学难题瓶颈

◇甘肃张瑛

整体思想是高中数学中的一种重要的思维模式,在解答高考的各类题型中都有可能使用到．教学中不难发现在教材中出现的诸多定理与公式的证明,都需要利用整体思想,由此可见整体思想在高中数学中占据着十分重要的地位．下面举例分析说明整体思想的应用．

1　整体代入,化繁为简

整体法,不是直接根据已知条件直接解决问题,而是从整体方面考虑．有些题目较为复杂,正常的思维模式根本无从下手,可通过对问题整体的把握,将其简单化后探索求解方式．

(n+1)an+1=nan．

①

整体考虑、整体代入,让问题变得清晰,使问题的解决变得快捷无比,我们又何乐而不为呢?

2　整体换元,巧求最值

整体换元是函数中经常使用的解题方法,通过构造新的函数,为学生展示一个新的解题思路．例如,在相关问题的教学中,可以给学生留下类似例2的练习题来锻炼学生的整体思维．

上述解题过程就利用了整体换元的思路,向着容易解决的方向变动．学生如果能够掌握这样的方法,既可节省时间、提高做题效率,思维模式也会得到锻炼与提升．这类题目就需要学生进行仔细观察,善于发现题目中整体存在的规律,将其视为整体，再根据新得到的函数将原有问题解决．

3　整体联动,数形结合

数形结合也是一种重要的解题思想,它通常与其他思维方法结合起来使用．某些代数问题如果只是采用代数的方法来解决会显得十分烦琐．如果换个角度,进行综合考虑、整体把握,问题就会化难为易了．

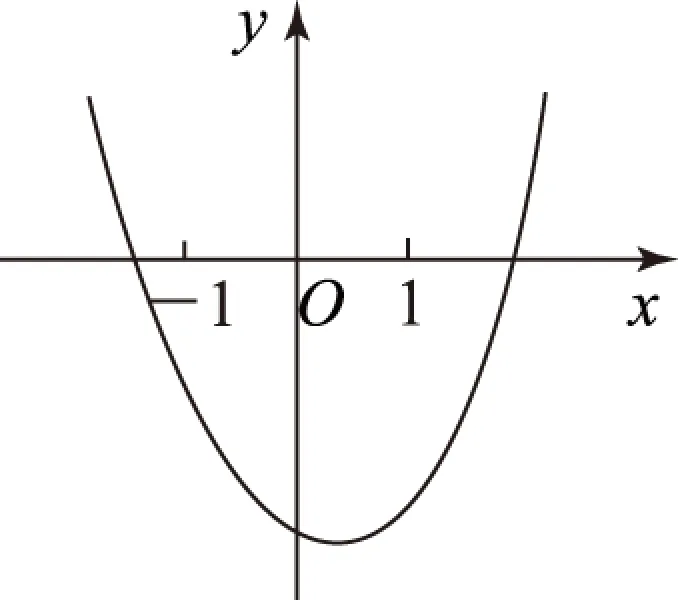
图1

本题体现了整体思想与数形结合思想的综合应用,教学中要让学生不断应用训练,才会使整体法在解题中融会贯通．

其实整体思想在数学中的应用,不仅仅限于上述那些方面,需要老师不断地去挖掘、归纳与提炼,学生接触的多,他们对整体思想的把握才会不断提升,数学思维也会得到训练．

甘肃省天水市第四中学)