燃烧室非线性压力振荡及其产生机理研究

汪广旭，付秀文，石晓波，刘占一，杨建文

（西安航天动力研究所，陕西西安710100）

燃烧室非线性压力振荡及其产生机理研究

汪广旭，付秀文，石晓波，刘占一，杨建文

（西安航天动力研究所，陕西西安710100）

当燃烧不稳定现象发生时，燃烧室内部往往伴随有较大幅值的压力振荡，其表现形式是非线性的。为了加深对其产生机理的认识，在能量平衡方法的基础上，通过求解包含高阶非线性项的各阶能量平衡方程，模拟了燃烧室非线性压力振荡曲线，给出了不稳定状态下，燃烧室压力的陡峭化过程以及各阶模态的“极限环”幅值分布。在此基础上，进一步对初始线性增长率α以及非线性效应对“极限环”幅值的影响规律进行了参数化研究，获得相应的分布规律曲线。最后，作为验证，对不同稳定工况下的“爆炸弹”压力振荡过程进行了数值模拟。研究表明，不稳定燃烧过程中，各阶模态之间存在相互作用，且随着α的增加，“极限环”幅值呈线性递增趋势，而非线性效应对“极限环”幅值的影响规律则相反。此外，“爆炸弹”数值实验表明，在进一步完善非线性项后，能量平衡方法具有模拟非线性燃烧不稳定现象的潜力。

燃烧不稳定现象，非线性压力振荡，能量平衡方法

0　引言

大量的试车和实验结果表明，实际的燃烧不稳定现象发生时，燃烧室内的压力振荡往往表现出明显的非线性特征，这些主要特征包括燃烧室压力的陡峭化过程、“极限环”幅值以及燃烧室平均压力的迁移现象等［1］。对以上特征所隐含的复杂机理进行分析研究将为深入理解燃烧不稳定现象提供重要切入点。例如，燃烧室压力的“陡峭化”过程说明其内部存在类似于弱激波形式的振荡，其压力变化曲线往往呈现N-型波特征（如图1所示）［2］。

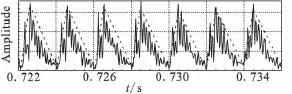
图1　燃烧室压力的N-型波特征Fig.1　N-type wave feature of combustion chamber pressure

本文采用的能量平衡方法起源于Kirchoff方程［3］，该方程给出了燃烧室不稳定压力振荡过程中的能量平衡关系。在此基础上，Cantrell&Hart以及Morfey等人先后考虑了均匀流和非均匀流效应，并由Myers推导了最终的解［4-11］。近年来，Flandro等人采用能量平衡方法研究燃烧不稳定方面取得了新的进展［12-17］。研究表明，基于Galerkin谱分解的二阶能量平衡方程能够给出决定系统稳定性的初始线性增长率αm，而更高阶的三阶非线性项的加入则使方程具有了描述不同模态间相互作用和影响的能力。通过求解代表不同模态间能量关系的方程组，可以获得燃烧室压力的理论演化曲线，从而能够很好地解释不稳定燃烧过程中燃烧室内压力振荡的一些重要的非线性特征。

1　能量平衡方法

为了分析不稳定燃烧过程中的能量关系，描述燃烧室流场的控制方程必须包含热传导、燃烧热释放、粘性应力和耗散效应等，其控制方程如下：

式中：H为总焓；m为质量流量；ω为涡量；ψ为单位体积内的体积应力，考虑了粘性剪切效应、膨胀效应和体积力等；Q为热释放。具体形式为：

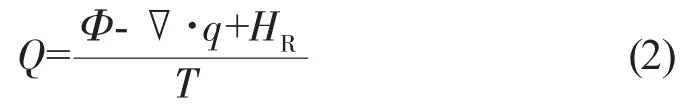
式中：q为热流通量；HR为燃烧热释放；Φ为耗散项。方程（1）表达了实际燃烧室中三种扰动传播形式：压力波、涡波、熵波。能量方程可以用方程（1）推导出来，具体形式为：

根据Kirchoff的理论，对于任何声学系统，其振荡能量的变化量与作用在系统上的功等于源项，其方程的具体表达式如下：

式中：E为系统振荡能量密度；W为作用在系统上的功；D为源项。因此，方程（3）理论上可以简化成方程（4）的形式。

Myers采用将均匀流变量分离的方法，给出了考虑非均匀流效应的能量准则 （Energy Corollary），并给出了上式中各项的具体表达式。进一步，引入声学分析方法，考虑将其中的变量分解成平均量和脉动量，并将脉动量展开成如下形式［15］：

式中：下标“0”为均匀流变量的稳态值；qn为n阶扰动量；ε为高阶小量。这样，在经过化简后可以获得各阶能量平衡方程。其中，零阶和一阶方程对于能量方程（3）恒成立，而二阶能量平衡方程可以用来评价系统的线性稳定性。

等熵情况下的二阶能量密度可以写成：

式中：前两项为Kirchoff声能量密度；第三项为均匀流引入的非定常量。相应地，二阶能量通量W2和源项D2为：

这样形成的二阶能量平衡方程为：

对上式进行空间积分和时间积分有：

为了对以上方程进行求解，需要给出各变量的扰动量形式。根据Galerkin谱分解思想，一阶压力扰动量可以写成：

无旋速度为：

式中：ψm为m阶声学模态的空间分布函数；x代表了空间位置；km为波数；γ为比热比。这样，方程（10）可以写成以下形式：

其中

对于纵向振型：

对于切向振型：

式中W′和D′分别为采用无量纲压力扰动幅值Rm归一化后的做功项和源项。如果认为各阶模态的初始幅值满足以下线性形式：

式中R0为初始幅值。代入方程（13）后可得：

初始线性增长率m是一个非常重要的参数。由方程（16）得到的 m包含很多子项［12-13］，主要包括喷注压力耦合效应、喷管耗散效应、热传导效应、边界层泵吸效应（Acoustic Boundary Layer Pumping）以及不稳定热释放等。αm中的每一项都需要单独讨论，其中的部分子项还没有明确的表达式，准确地给出该值仍然很困难。方程（16）可以进一步简化为：

假设初始一阶模态相对幅值为0.001，其他各阶模态幅值为0，则该线性方程给出的燃烧室各阶（纵向）模态幅值将会以图2所示的指数形式增长，而对应的压力会以图3所示的那样无限地增长。显然，这是不符合物理实际的，方程（17）需要考虑高阶非线性项。

图3　线性压力振荡过程Fig.3　Process of linear pressure oscillation

2　非线性压力振荡过程分析

为了简化讨论，忽略热传导效应，考虑等熵、无粘的燃烧室纵向压力振荡，并忽略二次流效应后的三阶能量密度项可以写成：

对其进行时间和空间积分后，带入方程（17）变为：

其中

方程（19）代表了各阶模态的能量平衡关系。在获得各阶模态的幅值Rm后可以根据方程（11）获得叠加后的脉动压力变化曲线。从方程（19）可以看出，三阶项引入了各阶模态之间的相互作用。同时，方程（19）也具有了描述燃烧室非线性振荡的能力。现考虑一阶模态驱动下的不稳定工况，并给定一阶模态增长率α1=200，αm=-400-200（m-1），（m=2，3，…，15），给定一阶模态幅值 R1（0）=0.05，αm=0，（m=2，3，…，15）。带入到方程（19）中计算得到的各阶模态幅值演化规律见图4。

图4　考虑非线性项后的各阶模态幅值Fig.4　Each order modal amplitudes considering the nonlinear term

与图2类似，一阶模态在初始阶段都经历了增长。在此之后，由于各阶非线性效应的加入，使得系统振荡幅值最终达到一个稳定值，该值称为“极限环”幅值。然而与图2所示不同的是，图4中其他各阶模态幅值也出现了增长，这一现象说明燃烧不稳定现象产生的非线性压力振荡会引起不同模态间能量的迁移现象。由图4进一步得到的压力变化曲线如图5所示。与实际情况类似，压力表现出了N-型波特征，其陡峭化的出现意味着模态间的相互作用得到了加强。

图5　燃烧室压力振荡“陡峭化”过程Fig.5　Steepening process of combustion chamber pressure oscillation

对于实际的不稳定燃烧问题，单纯地模拟出这些非线性特征显然是不够的，因为大部分的研究工作都希望能为工程实际提供指导。上文已经提到，αm综合考虑了不稳定燃烧的影响因素，其中包含了设计过程关心的重要参数。虽然目前还没有能力针对每一个影响因素进行讨论，但对αm进行定性的分析仍然是有意义的。为此，本文针对一阶模态驱动下的纵向燃烧不稳定现象进行了进一步分析，对不同α1驱动下的“极限环”幅值进行了计算，其结果如图6所示。从图6中可以看到，随着α1的增加，一阶模态的“极限环”幅值在升高，说明初始增长率的降低对抑制燃烧不稳定性有促进作用。

图6　一阶模态增长率α1对“极限环”幅值的影响Fig.6　Effect of linear growth rate 1 in first-order modal on"limited cycle"amplitude

从以上分析可以看出，非线性项的引入是能量平衡方法的关键环节，而模态间的相互影响是造成“极限环”幅值不能无限增长的主要因素。为了研究这种影响与“极限环”幅值的关系，本文引入非线性系数NF（Nonlinear Factor），使方程（19）变为：

即通过改变NF可以改变代表模态间耦合的非线性效应。“极限环”幅值随非线性系数的变化规律如图7所示。从图7可以看出，随着非线性系数的减小，“极限环”幅在不断增大，这说明模态间的相互作用是压力振荡趋于非线性化的重要诱因。

此外，由于本文采用了简单的柱形燃烧室结构以及纵向不稳定振型，与燃烧室具体几何相关的空间特征函数积分在方程（21）中被化简。然而，实际几何结构或者振型的影响仍然体现在方程（21）右端的非线性项中［15-16］。这些影响最终会体现在各阶模态的相互作用程度以及燃烧室压力的非线性特征上，从而改变燃烧系统的稳定性。事实上，现有的在液体火箭发动机燃烧室中加入隔板，通过改变其模态振型来抑制不稳定燃烧发生的思想与以上结论是一致的。从图7来看，如果改变燃烧室结构或者使振型朝着提高非线性效应的方向发展，则同样有助于提高燃烧系统的稳定性。

图7　非线性系数对“极限环”幅值的影响Fig.7　Effect of nonlinear factor on“imited cycle”amplitude

3　爆炸弹数值实验

实际的爆炸弹实验是用来衡量燃烧稳定性的重要方法，其压力振荡过程同样是非线性的。能量平衡方法同样具有模拟爆炸弹的能力。对于一阶模态驱动下的不稳定工况（α1=200）和稳定工况（α1=0.01），可以通过在无量纲时间（a/L）*t=37.5（a为声速，L为燃烧室长度）时引入各阶模态振幅的脉冲值（Rm=1.0）来实现爆炸弹过程，其压力振荡结果分别见图8和图9。对比两图可以发现，对于稳定工况，压力振荡会不断衰减，而不稳定工况下其振幅会达到有限值，这与预期的结果是一致的。

以上研究为模拟实际发动机试车曲线，为直观地分析发动机的稳定性结果奠定了基础，具有实际的工程意义。

图8　不稳定工况下的爆炸弹数值实验Fig.8　Numerical“bomb”test on unstable engines

图9　稳定工况下的爆炸弹数值实验Fig.9　Numerical test result of"bomb"under stable working condition

4　结论

本文采用能量平衡方法对燃烧室非线性压力振荡过程进行了数值模拟，并对主要影响因素进行了参数化研究。研究表明，初始模态增长率和各声学模态间的耦合对非线性压力振荡的“极限环”幅值具有重要影响，而各声学阶模态间的相互作用是导致燃烧室非线性压力振荡的重要诱因。也正是模态间的相互作用导致了能量在不同模态间的传递，进而抑制了驱动模态幅值的不合理增长。同时，本文采用能量平衡方法开展的“爆炸弹”数值实验证明：在进一步完善初始模态增长率后，该方法具有模拟真实发动机燃烧室压力振荡曲线的潜力。

［1］FLANDRO G A，SIMS J D.Nonlinear longitudinal mode instability in liquid propellant rocket motor pre-burner：AIAA-2004-4162［R］.Cincinatti，USA：AIAA，2004.

［2］FLANDRO G A，SIMS J D.On nonlinear combustion instability in liquid propellant rocket engines：AIAA-2004-3516［R］Cincinatti，USA：AIAA，2004.

［3］KIRCHHOFF G.Vorlesungen uber mathematische physik：mechanik［M］.Germany：Leibzig，1877.

［4］CANTRELL R H，HART R W.Interaction between sound and flow in acoustic cavities：mass，momentum，and energy considerations［J］.Journal of the acoustical society of America，1964，36（4）：697-706.

［5］HART R W，MCCLURE F T，Combustion instability：acoustic interaction with a burning propellant surface［J］. The journal of chemical physics，1959，10（6）：1501-1514.

［6］HART R W，MCCLURE F T，Theory of acoustic instability in solid propellant rocket combustion［C］// Tenth Symposium（International）on Combustion.Las Vegas，USA：AIAA，1964：1047-1066.

［7］SANDHAM N D，MORFEY C L，HU Z W.Nonlinear mechanisms of sound generation in a perturbed parallel jet flow［J］.Journal of fluid mach，2006，565（2）：1-23.

［8］MORFEY C L.Acoustic energy in non-uniform flows［J］. Journal of sound and vibrations，1971，14（4）：159-169.

［9］MYERS M K.Transport of energy by disturbances in arbitrary steady flows［J］.Journal of fluid mechanics，1991， 226（3）：383-400.

［10］MYERS M K.An exact energy corollary for homentropic flow［J］.Journal of sound and vibrations，1986，109（3）：277-284.

［11］MYERS M K.Generalization and extension of the law of acoustic energy conservation in a nonuniform flow［C］// AIAA 24th Aerospace Sciences Meeting.Sacramento，California：AIAA，1986：86-0471.

［12］FLANDRO G A，PERRY E H，FRENCH J C.Nonlinear rocket motor stability computations：understanding the brownlee-marble observations［C］//44th AIAA Aerospace Sciences Meeting and Exhibit.Fort Lauderdale，Florida：AIAA，2006：539-546.

［13］FLANDRO G A，JACOB E J.Irregular burning：on the origin of the DC shift［C］//43rd AIAA Joint Propulsion Conference.Las Vegas，USA：AIAA，2007：146-153.

［14］GLOYER P W，RICE T M，FLANDRO G A.Ares I thrust oscillation mitigation via motor modifications［C］//56th JANNAF Propulsion Meeting.USA：AIAA，2009：1110-1118.

［15］FLANDRO G，JACOB E.Finite amplitude waves in liquid rocket combustion chambers［C］//46th AIAA Aerospace Sciences Meeting.USA：AIAA，2008：111-119.

［16］FLANDRO G，FISCHBACH S.Effects of wave incidence on combustion instability driving mechanisms［C］//AIAA Joint Propulsion Conference.Cincinatti，OH：AIAA，2007：22-28.

（编辑：马杰）

Study on nonlinear pressure oscillation and its mechanism in combustion chamber

WANG Guangxu，FU Xiuwen，SHI Xiaobo，LIU Zhanyi，YANG Jianwen
（Xi'an Aerospace Propulsion Institute，Xi'an 710100，China）

When the combustion instable phenomenon happens，the high amplitude pressure oscillation often occurs simultaneously in combustion chamber，which behaves in nonlinear form.In order to make it more clear about the mechanism of production，the nonlinear oscillating curve for chamber pressure was simulated based on the energy balance method through solving the energy equations including high-order nonlinear term of each mode.The pressure steepening process and the distribution of“limited cycle”amplitudes in the unstable status are also presented.Based on this，the parameterized studyis conducted on the influence ofinitial linear growth rate α and the nonlinear effect on“limited cycle”amplitude，and the corresponding distribution curves are also showed in this paper.Then，as a validation，the pressure oscillating process of"bomb"under different stable conditions are simulated as well.It indicates that during the unbalanced combustion，interactive effects exist between the oscillating modes.Although"limited cycle"amplitude assumes progressive increase tendency with the increase of α the nonlinear effect on"limited cycle"amplitude has the opposite tendency.Except for this，the numerical experiment results show that if the nonlinear term can be further perfect properly，the energy balance method can be applied to the simulation of nonlinear combustion instable.

combustion instable phenomenon；nonlinear pressure oscillation；energy balance method

V434.13-34

A

1672-9374（2016）02-0029-06

2015-04-02；

2015-09-27

航天支撑技术项目（617010423）

汪广旭（1987—），男，工程师，研究领域为液体火箭发动机燃烧不稳定