基于M orlet小波函数的IDT建模与仿真
2016-11-09文理为曾志超牟庆丰王代强
文理为,曾志超,牟庆丰,王代强
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
基于M orlet小波函数的IDT建模与仿真
文理为,曾志超,牟庆丰,王代强
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
为了得到更精确的IDT结构模型,本文提出了基于Morlet小波函数的IDT数学模型,通过Matlab对其频响特性进行仿真分析,并与改进型δ函数模型IDT结构进行比较。结果表明,在相同的参数情况下,校正后的Morlet小波式IDT结构主瓣保持得很好,具有很好的通带性和主瓣波形,相对于改进型δ函数模型IDT结构,校正后的Morlet小波式IDT结构旁瓣电平得到大大的抑制,声电转换效率更高。
Morlet小波函数;IDT;Matlab;δ函数模型;频率响应
随着声表面波技术的快速发展,声表面波器件在电子信息等领域的应用越来越广泛,与此同时,为了满足现代通信技术高频化、微型化等特点,对声表面波器件的要求也越来越高:更高的响应频率、更高的带宽、更低的插入损耗以及更小的尺寸等[1-2]。叉指换能器(IDT)作为声表面波器件最重要的部分之一,要改善声表面波器件的特性,提高其性能,就必须从改进IDT结构入手[3-4]。首先建立IDT数学模型,再对其进行模拟仿真,并与传统模型仿真结果进行对比,改进模型参数以满足IDT结构优化的目的[5]。Morlet小波函数是一种单频复正弦调制高斯波,具有较好的时频特性对称性,在频域具有很好的线性相位特性,且其时频域局部性非常好,是最常用的复值小波,是分析信号的强有力工具[6]。文中是在IDT脉冲响应模型和改进型δ函数模型的基础上选择Morlet小波函数对IDT进行数学建模,再利用传统数学模型对同一IDT结构进行仿真对比,结果表明:校正后的Morlet小波函数的IDT模型比改进型的δ函数IDT模型更精确,达到预期结果。
1 M orlet小波函数型IDT的建立
1.1M orlet小波函数
小波函数有正交性和非正交性之分,Morlet小波函数是一种非正交波,不存在尺度函数,其数学表达式为[7]:

其中,ω0为小波的中心频率。对(1)式进行傅里叶变换,得其频率响应:
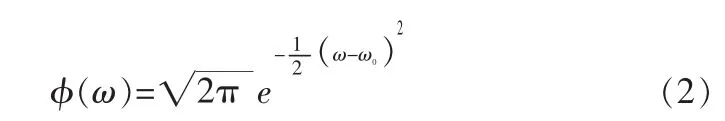
由于小波函数是处理信号的工具,SAW是变化缓慢的信号,又由于小波函数的时频窗是灵活伸缩的,因此用此特性就能灵活的设计IDT结构[8]。
1.2改进型IDT的δ函数模型
贵州大学王代强教授提出了一种改进型δ函数模型[9],如图1(b)所示,在IDT结构中用边长为aik的若干正方形来表示一根指条,并将每个正方形看作一个独立的声波激发源,假设有k个正方形,每个声波激发源用基本的δ函数单元表示,再将整根叉指指条激发的SAW进行归一化处理。
为了表达得更明确,选取一个规则型等间距的IDT结构进行分析。在IDT结构的中心取一坐标原点x=0,如图1(a)所示。同时,由于IDT结构可看作横向滤波器,则对其场源分布进行傅里叶变换可求出整个IDT结构的频率响应为[10]:
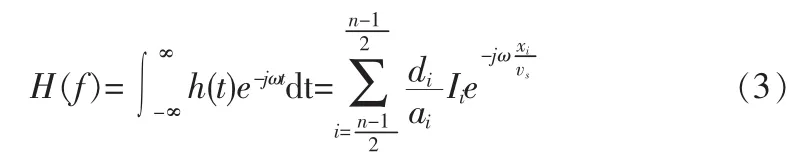
上式中,ai表示第i根叉指电极的宽度,di表示第i根叉指电极的长度,xi表示第i根叉指电极的位置,vs表示SAW的传播速度,Ii表示第i根叉指电极的声波幅值。
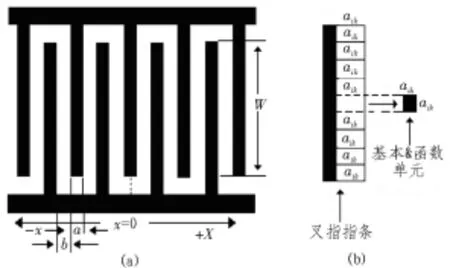
图1 改进型IDT结构δ函数模型
1.3M orlet小波式IDT结构模型
文中是在IDT的脉冲响应模型和改进型δ函数模型的基础上提出的基于Morlet小波函数的IDT模型。构造Morlet小波函数IDT的基本思想是IDT可看作横向滤波器,因此,首先将想求解的的频率响应函数H(f)进行变换,得到相应的脉冲响应函数h(t)[11]。根据抽样定理,以1/4f0对脉冲响应函数h(t)均匀抽样,然后用小波函数φ(t)截断,在小波函数窗口内得到有限长度φ(tn)·h(tn)。为了对IDT最终频响进行精度调整,要求计算的频率响应比常规方法计算的精度更高,因此采用时域上对脉冲响应直接奇偶分解与小波窗函数截断相结合的方法研究IDT结构[12-13]。根据网络脉冲响应函数理论,因为IDT的脉冲响应与它的结构之间有着密切的关系,很自然地想到用脉冲响应函数去描述分析IDT结构。在滤波器理论的基础上,脉冲响应和频率响应之间互为傅里叶变换对,可由需要的频响函数得到相应的脉冲响应函数[14]。
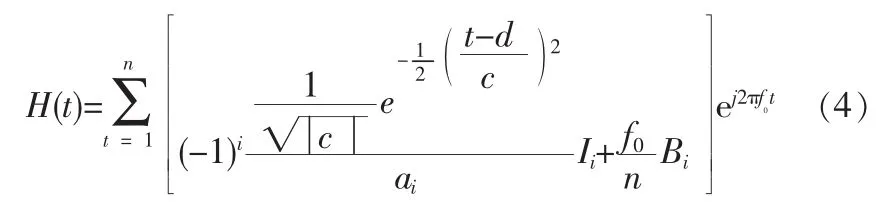
当Morlet小波函数的伸缩因子c=1,平移因子d=0时,(4)式中的脉冲响应函数h(t)对应的IDT结构为Morlet母小波式IDT结构模型。(4)式中的脉冲响应表达式是频率响应函数校正后的结果,若不进行频率响应函数的校正,那么h(t)结果为:
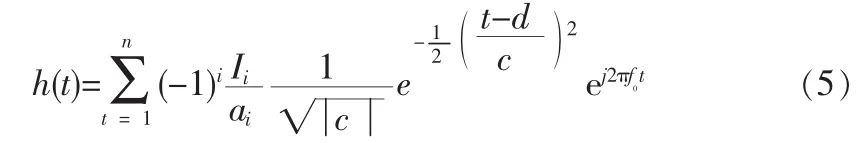
我们知道,在改进型的δ函数模型中,为了计算更加简单方便,选取IDT结构的中心为一坐标原点x=0。同时,对于一个电极间隔b均匀的IDT结构,不管IDT结构是否被加权,它的频率响应都是对称的,因此为了计算简单方便,也取Morlet母小波式IDT中心为坐标原点,则整个Morlet小波式IDT的脉冲响应为:
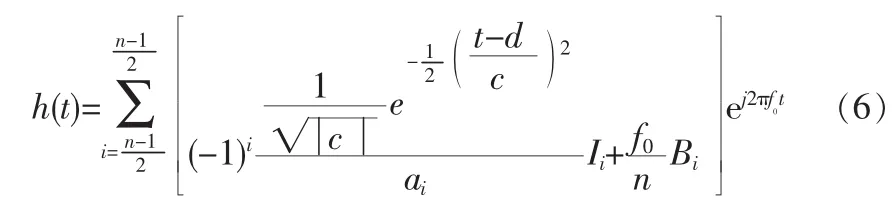
采用1/4f0对式(6)抽样,其抽样序列为:

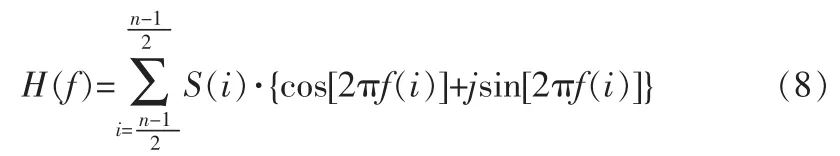
由上式可知,整个Morlet小波式IDT结构的脉冲响应函数是奇偶分量与校正函数之和,当中心频率为f0时,只剩下偶分量和频率响应的调整函数。根据脉冲响应函数与频率响应函数之间的关系,当IDT结构的声孔径长度按照Morlet母小波函数设计时,小波式IDT结构脉冲响应函数偶分量所对应的频率响应为:
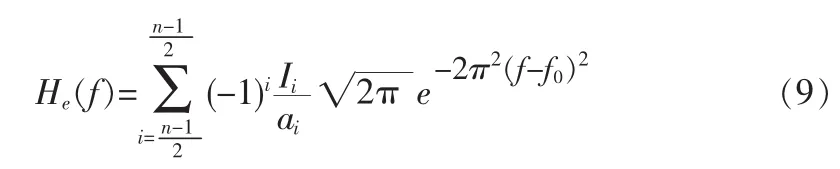

式中,Bi为第i根叉指电极的校正函数幅度,可以取正负值,fi为第i根叉指电极校正函数的调整点频率。将(9)与(10)两式相加,即:
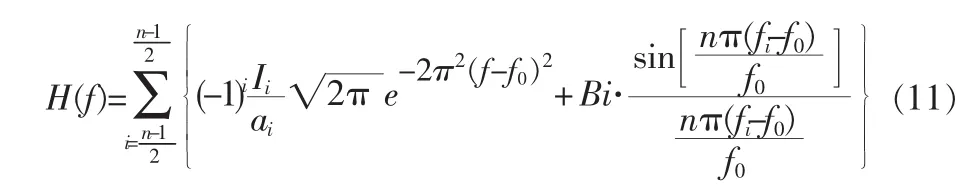

2 IDT的M orlet小波函数模型仿真
2.1IDT的M orlet小波函数模型结构参数
为了能够设计出IDT结构,求解出小波式IDT的叉指电极位置以及相邻叉指间隔很关键,同时还需确定IDT结构的叉指电极数和中心频率f0。而叉指换能器的指条位置与基片材料的选取以及时间有关,其关系如下:

在IDT结构中,基片材料确定后,SAW的传播速度vs也就确定了。因此中心频率f0可由下式确定:

对于均匀的IDT结构,通常取ai=bi。我们知道叉指电极数n也是决定IDT结构性能好坏的参数之一,叉指电极数不但影响着声波的激发强弱,也影响着带宽,在IDT结构中要根据实际情况来确定其个数。
2.2仿真分析
在IDT结构中,设每一根叉指电极有k个基本δ信号源,而且每根叉指电极产生的信号源强度与其声孔径Wi(t)成正比,由于SAW的激发强度仅与声孔径有关,因此在本文中,将其声孔径按照Morlet小波函数设计时,声孔径是可变化的,这样就能够得出不同的小波式IDT结构[15]。最后结合改进型δ函数模型以及IDT结构的脉冲响应模型得出其小波式IDT结构的频率响应。
根据改进型δ函数对规则IDT结构的建模,采用Matlab数学工具,其中取叉指宽度a=7.5μm、叉指间隔b=7.5μm、叉指对数N=45,根据规则型IDT的频率响应表达式(3),得其结构的频率响应,如图2所示。同时保持参数值不变,根据(6)式,用Matlab数学工具,仿真得到Morlet母小波式IDT的频率响应图形,如图3所示。

图2 规则型IDT结构频响仿真图
对比图2和图3,可见Morlet小波式IDT在与规则的δ函数型IDT具有同样的叉指电极时,它们的带宽大体一样。但是Morlet小波式IDT结构的通带性及主瓣波形较好,相对于规则型IDT结构,Morlet小波式IDT结构的第一旁瓣电平抑制从38.5 dB提高到41.9 dB,第二旁瓣电平抑制从42.1 dB提高到43.7 dB,第三旁瓣电平抑制从43.6 dB提高到46.9 dB。
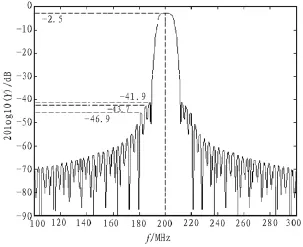
图3 Morlet小波式IDT频率响应仿真图
若对 Morlet小波式 IDT结构频响进行校正,根据式(11),所取参数值与上面的相同,用Matlab作为数学工具将频率响应仿真出来,可以得到校正后的Morlet母小波式IDT结构的频率响应如图4所示。
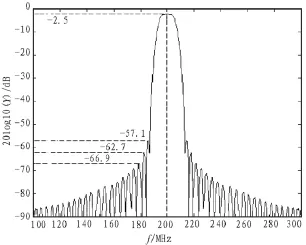
图4 Morlet小波式IDT频率响应校正后的仿真图
对比图3、图4,经过校正后的Morlet小波式IDT结构与规则型IDT结构在叉指电极对数N相同、指宽以及间距都保持一样时,带宽能够保持大体相同,同时,其主瓣可以保存的更好,衰减更小,有较好的通带性,而且旁瓣电平得到了更好的抑制,第一旁瓣电平抑制从38.5 dB提高到57.1 dB,第二旁瓣电平抑制从42.1 dB提高到62.7 dB,第三旁瓣电平抑制从43.6 dB提高到66.9 dB。由于在IDT结构中其频率响应的谐振峰高度与叉指电极对数N成正比,宽度与叉指电极对数N成反比,可见校正后的Morlet小波式IDT结构具有更高的声电转换效率,频率响应特性更好。在生产中,可以根据实际情况,根据带宽、中心频率、实际滤波的需要有选择的挑选所需要的IDT结构。
3 结 论
文中是在IDT的脉冲响应模型和改进型的δ函数模型的基础上提出了Morlet小波函数的IDT数学模型,采用Matlab对IDT的Morlet小波函数模型以及改进型δ函数模型的频响特性进行仿真分析、比较。结果表明,改进型δ函数型IDT结构和校正后的Morlet小波式IDT结构在叉指电极对数N相同、指宽以及间距都保持一样时,可以取得相同的带宽,同时,校正后的Morlet小波式IDT结构主瓣保持得更好,衰减更小,通带性也很好,相对于改进型δ函数型IDT结构,校正后的Morlet小波式IDT结构旁瓣电平得到大大的抑制,其第一旁瓣电平抑制提高了18.6 dB,第二旁瓣电平抑制提高了20.6 dB,第三旁瓣电平抑制提高了23.3 dB,这一结果说明Morlet小波式IDT结构具有比改进型δ函数型IDT结构更高的精确度。
[1]徐希嫔,王代强,刘桥.阶梯型IDT结构的仿真研究[J].现代电子技术,2009(6):176-177.
[2]王代强,姚祖明,陈雨青,等.圆形IDT结构声表面波滤波器的设计与实现[J].电子元件与材料,2013,32(4):50-53.
[3]王代强,陈雨青,徐希嫔,等.变迹加权三角形IDT结构的SAW滤波器设计与实现[J].西南大学学报:自然科学版,2011,33(7):31-35.
[4]王代强,陈雨青,姚祖明,等.硅基AlN椭圆形IDT-SAW滤波器的设计[J].传感技术学报,2013,26(12):1691-1694.
[5]魏培永,朱长纯,刘君华.用声表面波器件实现小波变换[J].压电与声光,2001,23(3):173-175.
[6]罗光坤.Morlet小波变换理论与应用研究及软件实现[D].南京:南京航空航天大学,2007.
[7]何岭松,李巍华.用Morlet小波进行包络检波分析[J].振动工程学报,2002,15(1):119-121.
[8]LI Yuan-yuan,LU Wen-ke,GONG Lin-jia.The research of wavelet transformation technology by using surface acoustic wave devices[J].IEEE Conference Publications,2011,3:926-929.
[9]王代强,陈雨青,徐希嫔,等.SAW器件叉指换能器δ函数模型的改进[J].电子元件与材料,2010,29(9):62-65.
[10]Hashimoto K,Yamaguchi M.Derivation of coupling-of-modes parametersforSAWdeviceanalysisbymeansof boundaryelment method[J].IEEE Ultrason.Symp.,1991,1: 21-26.
[11]张晓庆.高频声表面波滤波器的纳米压印技术制备研究[D].武汉:华中科技大学,2011.
[12]赵义祯.声表面波滤波器的设计及其衍射补偿的研究[D].杭州:浙江工业大学,2007.
[13]董辉平.声表面波传感器模拟与仿真[D].太原:中北大学,2008.
[14]冯亚菲.声表面波器件的制备及其性能研究[D].哈尔滨:黑龙江大学,2008.
[15]董溯前.声表面波式小波变换器件的研究[D].上海:东华大学,2008.
Modeling and simulation of IDT based on Morletwavelet
WEN Li-wei,ZENG Zhi-chao,MOU Qing-feng,WANG Dai-qiang
(College of Big Data and Information Engineering,GuiZhou University,Guiyang 550025,China)
In order to obtain a more accurate IDT(Inter Digital Transducer)structure,a new IDT mathematicalmodel is presented,based on Morlet wavelet function.Compared with the modifiedδfunction model IDT of its frequency response characteristics by Matlab.The results shows,in the case of the same parameters,the adjusted Morletwavelet IDT'smain lobe kept well,with good passband and the main lobe of the waveform.Compared with the modifiedδfunction model IDT,the sidelobe levelwasgreatly suppressed,and ithasa higheracoustic-electric conversion efficiency.
Morletwavelet function;IDT;Matlab;δfunctionmodel;frequency response
TN65
A
1674-6236(2016)19-0007-04
2016-03-14稿件编号:201603158
国家自然科学基金项目(11564005)
文理为(1992—),男,湖南醴陵人,硕士研究生。研究方向:声表面波器件,电路与系统。
