含裂纹悬臂梁的振动特性分析

孔　成，续秀忠

（上海海事大学 物流工程学院，上海 201306）

含裂纹悬臂梁的振动特性分析

孔成，续秀忠

（上海海事大学 物流工程学院，上海 201306）

用一无质量扭转弹簧来模拟裂纹所在截面，这样就可以将裂纹梁分为两段研究。基于两段完整的梁的振型表达式，推导出了裂纹梁的传递矩阵，进而给出悬臂裂纹梁的频率方程。用Matlab软件编程求解悬臂裂纹梁的频率方程，把所得结果与有限元结果进行对比分析，研究裂纹位置和裂纹深度对悬臂裂纹梁固有频率的影响，验证了推导方法的合理性。

振动与波；裂纹梁；传递矩阵；固有频率；Ansys；Matlab

在机械工程领域，裂纹的检测与识别对于保证设备的正常运转，预防突发事故具有十分重要的意义。在过去几十年，许多学者对裂纹检测方法做了广泛的研究，如超声检测法、声发射法和频域法［1-2］等，这些方法在裂纹检测上已取得了很好的效果，但这些方法难以定量分析，识别准确度不高［3］。基于振动特性的损伤检测近年来越来越受到重视［4］，因为结构损伤会对振动系统的动态特性产生影响，使得振动系统的有关参数发生改变，如固有频率和振型将发生相应的变化，这具有重要的工程意义。

过去几十年，许多学者对裂纹梁固有频率的计算做了广泛的研究，并获得了许多计算裂纹梁固有频率的方法［5-6］。本文对裂纹所在截面用一无质量扭转弹簧来代替，这样就将含裂纹的悬臂梁分为两段完整的梁，基于梁的振型表达式，推导出了裂纹悬臂梁的传递矩阵，结合具体的边界条件给出了悬臂裂纹梁的频率方程，用Matlab编程方法求解了悬臂裂纹梁的频率方程。并就裂纹悬臂梁进行了数值模拟，研究了裂纹位置和裂纹深度对固有频率的影响。

1　裂纹梁传递矩阵

悬臂梁的自由振动方程［7-8］

式中EI——梁的弯曲刚度；ρ——梁的密度。由于梁的振型与时间无关，所以设代入式（1），得

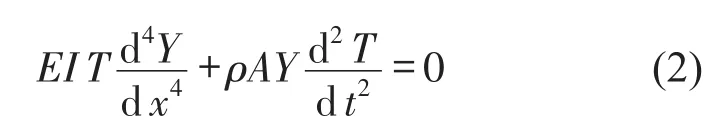
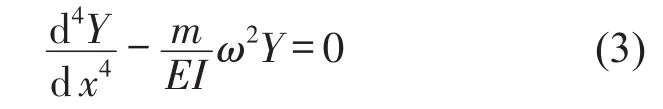
方程（3）的解具有如下形式

对于悬臂梁的裂纹截面，我们可以将其看成是由两根梁通过一扭转弹簧连接［9］，如图1所示。

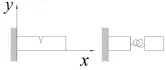
图1　裂纹梁模型及其等效模型

这样悬臂裂纹梁被分成了两段，其振型可写为

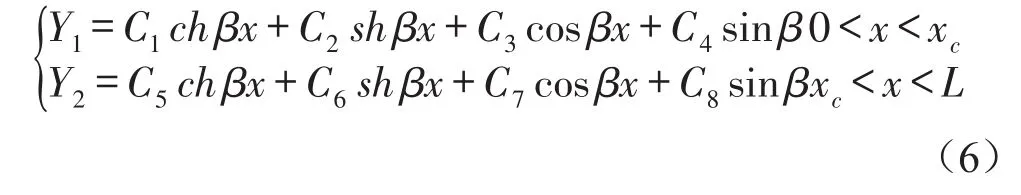
式中C1～C8——常数；xc——裂纹所在截面的横坐标。

由Dimarogonas和Paipeties理论［10］，在裂纹处其挠度、剪力和弯矩是连续的，而转角不连续。转角满足的条件为

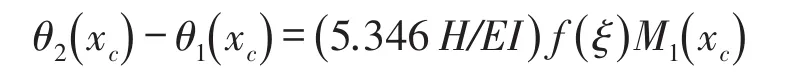
式中ξ=a/H——相对裂纹深度；f（ξ）——柔度函数，可由应变能密度函数求得

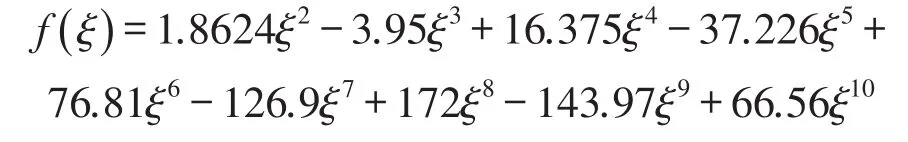
裂纹两边的挠度、转角、弯矩以及剪力满足关系

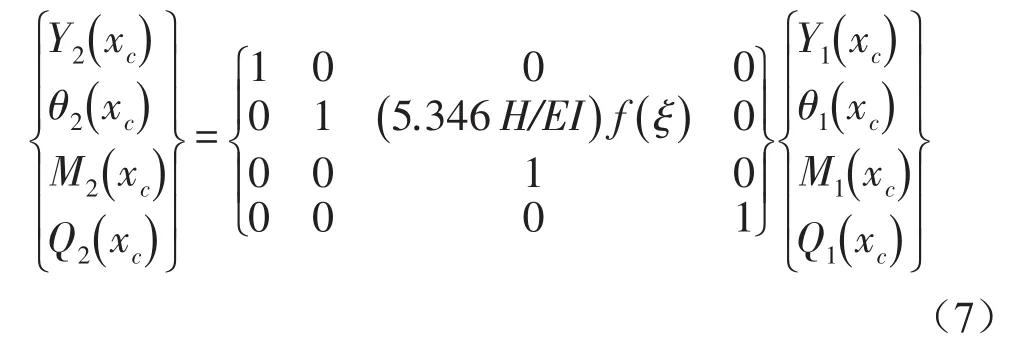
根据完整梁振动问题的传递矩阵解法知

式（10）就是裂纹梁的传递矩阵。

把传递矩阵写成如下形式

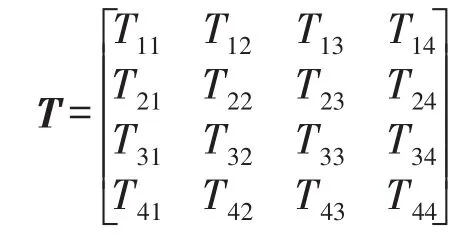
由悬臂梁的边界条件

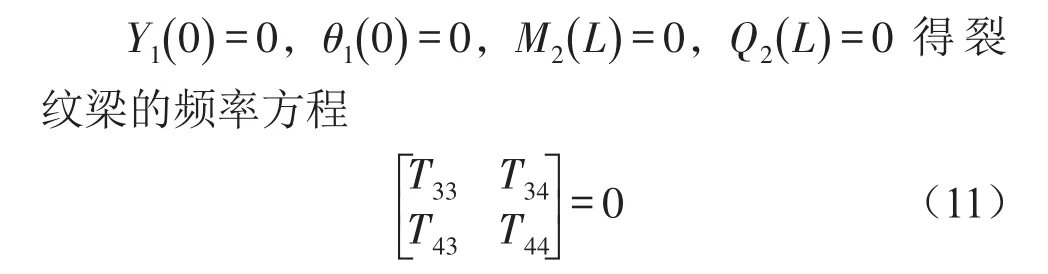
2　算例分析

2.1传递矩阵方法

应用前述推导的传递矩阵法，结合悬臂梁的边界条件得到了方程（11），运用Matlab软件对方程（11）进行求解，从而对悬臂裂纹梁进行数值计算，计算中使用的几何参数和材料常数为长L为0.3 m，截面尺寸宽b为0.02 m，高h为0.02 m，材料的弹性模量200 GPa，泊松比为0.3，质量密度为7.85×103kg/m³。

令Q=T33×T44-T43×T34，编制Matlab程序，求解这个函数会得到一条以频率作为自变量的函数曲线，函数曲线如图2所示。

函数的零点就是方程（11）的根，也就是我们所需要的固有频率值。

裂纹深度为定量，裂纹深度a=0.002 m时，通过改变裂纹的位置，来计算裂纹在不同位置时悬臂梁的1阶固有频率。表1列出了不同裂纹位置下的悬臂梁1阶固有频率：

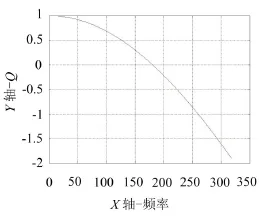
图2　关于频率的函数曲线

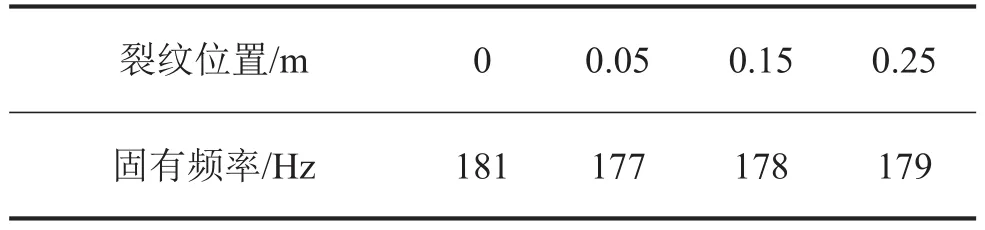
表1　不同裂纹位置时的1阶固有频率（裂纹深度0.002 m）

裂纹位置为定量，裂纹位置x=0.15 m时，通过改变裂纹的深度，来计算裂纹在不同深度时悬臂梁的1阶固有频率。表2列出了不同裂纹深度下的悬臂梁1阶固有频率。

表2　不同裂纹深度时的1阶固有频率（裂纹位置0.15 m）

从传递矩阵法的计算结果来看，当裂纹深度为定值时，裂纹位置的改变也会引起固有频率的改变。随着裂纹位置远离梁的固定端，其固有频率在增大，与正常悬臂梁固有频率相比，其固有频率的减小量在缩小，如表1所示。当裂纹位置为定值时，裂纹深度的改变也引起了固有频率的改变。随着裂纹深度的增大，其固有频率在不断减小，如表2所示。

2.2有限元方法

对悬臂梁进行有限元分析，有限元模型和单元划分，如图3所示。模型的几何参数和材料常数与上文中使用的参数保持一致。分析中使用Shell单元，就悬臂梁进行计算。计算结果列于表3和表4。如表3所示，在裂纹深度为定量时，不同裂纹位置时悬臂梁的1阶固有频率；如表4所示，在裂纹位置为定量时，不同裂纹深度时悬臂梁的1阶固有频率。

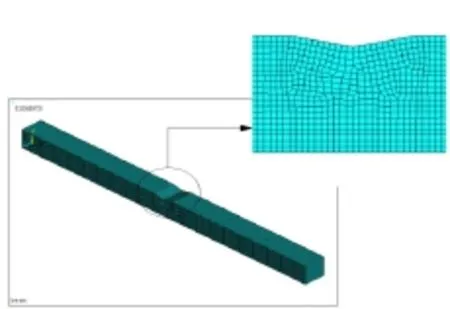
图3　裂纹梁有限元模型

表3　不同裂纹位置时的1阶固有频率（裂纹深度0.002 m）

表4　不同裂纹深度时的1阶固有频率（裂纹位置0.15 m）

从图4和图5可以看出，本文的计算结果与有限元计算结果基本吻合，计算各组数据之间的误差，其误差均在1%左右，误差较小，说明准确度较高，验证了本文推导方法的合理性。

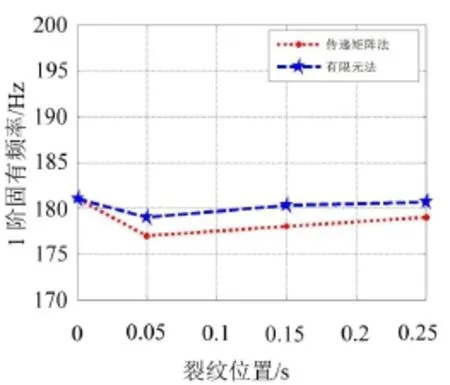
图4　不同裂纹位置时的1阶固有频率

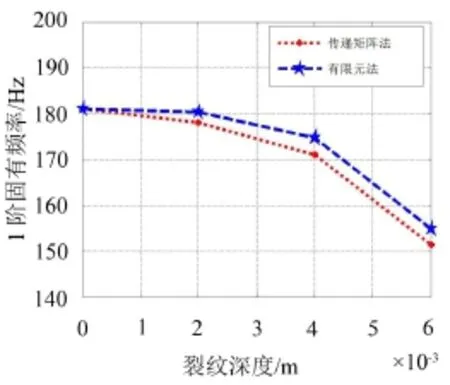
图5　不同裂纹深度时的1阶固有频率

3　结语

本文推导了含裂纹的悬臂梁的传递矩阵，并给出了悬臂裂纹梁的频率方程。通过用Matlab编程的方法求解悬臂裂纹梁的频率方程，得到了含裂纹梁的固有频率。针对同一算例应用有限元方法，同样得到了含裂纹梁的固有频率。将两种方法的结果进行对比，验证了本文所推导理论方法的合理性，同时也得到了如下结论：

（1）当裂纹深度为定值时，随着裂纹位置远离梁的固定端，其固有频率在增大，与正常悬臂梁固有频率相比，其固有频率的减小量在缩小。

（2）当裂纹位置为定值时，随着裂纹深度的增大，其固有频率在不断减小。

［1］王金福，李富才.机械故障诊断的信号处理方法:频域分析［J］.噪声与振动控制，2013，33（1）：173-180.

［2］孟范孔，邱志成.梁损伤小波包分析和神经网络识别［J］.噪声与振动控制，2013，33（1）：197-200+207.

［3］张敬芬，赵德有.工程结构裂纹损伤振动诊断的发展和展望［J］.振动与冲击，2002，21（4）：22-26.

［4］李兵，陈雪峰.基于小波有限元的悬臂梁裂纹识别［J］.振动工程学报，2004，17（2）：159-164.

［5］陈梦成，汤任基.一种裂纹梁振动响应分析的近似方法［J］.应用数学和力学，1997，18（3）：204-209.

［6］李学平，余志武.含多处裂纹梁的振动分析［J］.应用力学学报，2007，24（1）：66-69.

［7］张佐辉，李学平.存在裂纹梁的动力分析［J］.长沙铁道学院学报，2003，21（2）：105-108.

［8］苟兵旺，刘永寿，等.轴向压力影响下裂纹梁振动特性分析［J］.机械设计与制造，2009（12）：211-213.

［9］RIZOS P F，ASPRAGATHOS N，DIMAROGONAS A D. Identification of crack location and magnitude in a cantilever beam［J］.Journal of Sound and Vibration，1999，138:381-388.

［10］DIMARONAS A D PAIPETIES S A.Analytical methods in rotor dynamics［M］.Elsevier applied science，London，1983.

Analysis of Vibration Characteristics of Cracked Cantilever Beams

KONGCheng，XU Xiu-zhong
（College of Logistics Engineering，Shanghai Maritime University，Shanghai 201306，China）

Simulating the cracked section by a massless torsion spring，the cracked cantilever beam can be divided into two sub-beams.Based on the vibration modes of the two sub-beams，the transfer matrix of the cracked cantilever beam is obtained.Frequency equation of the cantilever beam is given and solved by Matlab.The results are compared with those of finite element method.The effect of crack location and crack depth on the natural frequency of the cantilever beam is analyzed.The rationality of this method is verified.

vibration and wave；cracked beams；transfer matrix；natural frequency；Ansys；Matlab

TH113；O322

ADOI编码：10.3969/j.issn.1006-1335.2016.05.007

1006-1355（2016）05-0031-03+50

2016-05-06

上海海事大学研究生创新基金资助项目（2015ycx036）

孔成（1989-），男，江苏省泰兴市人，硕士生，主要研究方向为机械动态性能监测。E-mail:kong6616@163.com

续秀忠，男，副教授，硕士生导师。E-mail:896534896@qq.com