基于单目三维重构的空间非合作目标相对测量

李永飞，王仕成，杨东方，孙大为

火箭军工程大学 控制工程系，西安 710025



基于单目三维重构的空间非合作目标相对测量

李永飞，王仕成，杨东方*，孙大为

火箭军工程大学 控制工程系，西安 710025

为了解决非合作目标的相对测量问题，提出了一种基于单目图像序列目标重构结果的非合作目标相对位姿测量方法。该方法将目标的三维重构与相机的位姿信息计算相结合，首先利用观测前期得到的图像序列，通过非线性优化算法计算得到目标上部分三维点坐标；然后基于该三维点集合，建立递推深度模型，对相机的相对位姿信息和新观测到的目标点同时进行卡尔曼滤波估计。航拍测量试验表明，随着图片数量的增多，精确重构点的比例(重投影误差小于1个像素的点)不断提高，80%的图像中精确重构点比例优于89%；基于公共数据集的试验表明，该算法对姿态估算精度可达1°以内，位置测量的精度可达到2 cm以内。以上试验结果表明，该算法具有较高的测量精度。

目标重构；相对位姿测量；单目视觉；非合作目标

空间测量是空间遥操作、空间交互对接等航空航天领域的一项关键技术[1]。早期的空间测量传感器主要包括激光、红外等距离传感器，这类传感器存在价格高，功耗高、体积庞大等缺陷，将其应用于一些成本低、体积小的空间机器人或者小型对地测量平台等领域中受到很大的限制[2]。近年来，随着计算机视觉技术的发展，其在成本、可视化等方面存在的优势受到越来越多学者的关注，仅仅依靠小型视觉传感器实现空间非合作目标相对测量成为近年来的研究热点[3]。

根据传感器的不同，视觉测量可以分为多目视觉测量系统、双目视觉测量系统和单目视觉测量系统。其中，多目视觉测量系统和双目视觉测量系统结构复杂，需要标定相机间的相对位姿；由于标定工艺复杂，成本较高，而且标定过程中引入的误差难以消除[4]。因此本文主要针对单目视觉系统进行研究。

单目位姿估计算法的研究主要包括两类：线性约束法和非线性优化法。线性约束法给定相邻时刻针对同一三维场景的两幅图像，通过特征点的提取和匹配，利用摄像机对极几何约束关系，能够在相差一个非零因子的意义下求解运动参数(R,t)。早期相关论文研究很多，从最早的8点算法，7点算法，到2004年Nister提出的5点算法[5]，人们通过对极约束模型进行分析，不断降低了位姿计算的复杂度。然而，线性约束法对于图像中的噪声数据非常敏感，往往不能得到理想的位姿估计结果。因而，此后对摄像机位姿估计方法的研究主要为非线性递推算法[6-7]及光束平差法[8-10]。虽然，这类非线性优化方法能够在给定良好初始值的情况计算得到较精确的结果；但是，这类非线性优化方法存在明显的不足，针对非凸问题目前仍然没有有效的优化算法能够保证其最优解的获取，这样得到的位姿估计结果往往容易陷入局部最优[11]；并且往往由于观测点较多，使得需要优化的变量的维数很高，计算变得复杂，无法满足相对测量实时性的要求。

为此，本文提出了一种实时高精度的非合作目标测量方法，该方法先采用非线性优化的方法，重构出较精确的非合作目标三维点集，随后以此为初始三维点集，采用滤波的方法，实现目标相对位姿测量和增量式的三维重构，充分利用对目标观测的全部信息，提高了相对测量的鲁棒性和精度。

1　问题描述

1.1射影相机模型

目前常用的相机模型是针孔相机模型，它可以被定义为一个将世界坐标系的三维点X，映射到图像坐标系像素点的一个射影变换，如图1所示，可以用矩阵P来表达该射影变换。对于任一世界坐标系中的点X，其世界坐标系中的坐标和图像坐标系中的坐标的转换关系为

(1)

摄像机模型确定了世界坐标系中特征点及其成像坐标之间的关系，这也是进行视觉位置和姿态测量的基本依据。传统的位姿估计算法需要已知特征点的三维坐标，即式(1)中方程最右边的特征点向量。然而，在本文所研究解决的问题中，空间目标是非合作目标，因此，其真实世界坐标也是未知的，无法直接计算相对位姿参数。为此，本文提出：能不能利用图像序列，完成非合作目标的重构后，再进行相应的单目视觉位姿计算，完成单目视觉相对测量呢？这也就是本文所提方案的初衷。

1.2非合作目标相对测量

在合作目标的空间相对测量过程中，利用事先设定的参考标志信息，结合前述摄像机成像几何模型，计算摄像机和目标之间的相对位姿关系。然而，对于非合作目标而言，由于目标物体上没有已知的标志物信息，甚至连基本尺寸信息都是缺失的，如图2所示。

图2　合作目标和非合作目标测量任务对比示意Fig.2　Comparison between relative measurement for cooperation target and that for non-cooperation target

为了完成这类非合作目标的相对测量，当前的研究往往都是基于目标某些先验信息已知的假设，例如文献[12-13]。为了适应于更加一般且真实的应用场景，本文针对被测目标是完全未知的情形进行研究。

2　增量式非合作目标重构测量算法

本文提出的非合作目标测量算法分为两个阶段。第一阶段，对观测的图像进行捆绑约束的非线性优化，得到目标的三维点坐标集；第二阶段，以第一阶段得到的三维点集为初始三维点集，采用滤波的方法，增量式优化求解相对位姿关系和新观测的三维点坐标。

2.1基于图像序列的目标三维重构

对于单目视觉系统而言，为了根据所拍摄的图像序列完成对目标的三维重构，需要利用不同时刻所采集的图像，重构出目标的空间坐标，利用时间域的扩展实现空间域信息的重构。在测量任务第一阶段，利用对目标的多位置、多角度观测得到的图像可以重构出目标的三维点云坐标。该问题可以描述为：已知相机在m个不同位置k(k=1,2,…,m)对n个点Xi(i=1,2,…,n)进行观测，观测结果由(uki,vki)表示，求世界点Xi和各个位置相机的位姿参数(Rk,tk)。

为解决上述问题，本文采用Gerald Schweighofer等于2008年提出的一种具有全局收敛性的相机运动参数的估计方法[14]。该方法基于通用相机模型[15]，对于单目针孔相机系统，通用相机模型可等价表达为

(2)

式中：(c,v)为由通用相机模型表达的测量结果；K为相机的内参数矩阵；R、t分别为相机相对于世界坐标系的旋转矩阵和平移向量；p为图像的像素坐标。

基于以上转换关系，选取目标空间重构误差作为代价函数，该方法可以表达为求代价函数E(R,t,X)的最小值的问题，即：

(3)

该方法首先求解出由位姿参数R,t表达的世界点坐标最优解X=X(R,t)；其次，求解出由旋转矩阵R表达的平移向量最优解t=t(R)；最后，将代价函数表达成旋转矩阵R的函数并给出求最优解的递推算法R(λ+1)=R(R(λ),t(λ),X(λ))。具体计算过程如下：

(1)世界点的三维坐标最优解

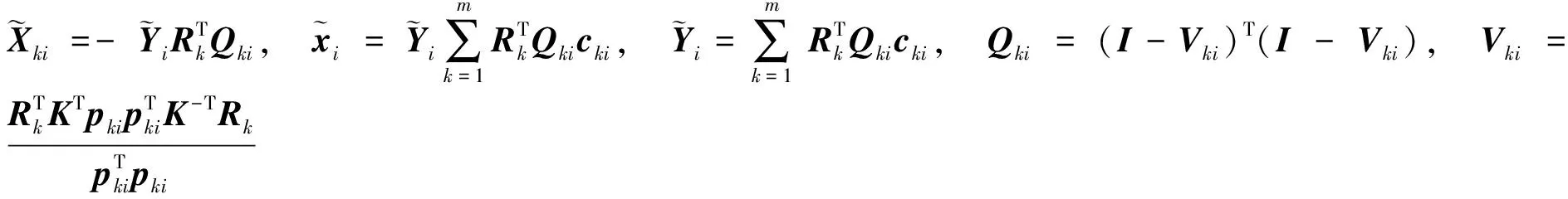
(2)平移向量最优解

At,bt分别为m个具有如下

形式的等式联立得到的方程组的系数矩阵和常数项矩阵。

(3)旋转矩阵的求解

在最优解(1)、(2)结果的基础上，该问题可表达为

(4)

其中，

对该问题进行递推求解，记第λ次的迭代结果为

(5)

(6)

由以上步骤，可以求出三维世界点云坐标，得到较精确的目标三维点集。

需要指出的是，上述得到的三维点坐标，是相对于固定世界坐标系的相对位置坐标。在本文中，该世界坐标系便是初始时刻的摄像机光心坐标系。

2.2增量式重构测量算法

前述过程完成了目标三维点云模型的重构，虽然上述方法经证明能够取得较为准确的重构精度，然而，需要指出的是，上述方法中，只能对图像集合进行捆绑优化处理，不能实现图像序列的序贯处理，这对于常用的目标相对测量任务而言是不能满足需求的。为此，本节以该初始化模型为基础，提出了一种增量式的重构测量算法。该算法首先根据初始化重构得到的三维点集，利用摄像机成像几何关系，得到相机相对目标的位置和姿态参数信息；然后，利用该位姿参数信息，对每一帧新采集的图像进行特征点重构，随后，再利用该重构优化后的点云结果，反过来辅助下一个时刻摄像机位姿参数的计算。从上述过程可以看出，该方法实际上是一个图像序列序贯处理的过程，随着图像序列的增加，重构精度经过不断优化越来越高，而摄像机相对目标的位姿参数的精度也随之逐步提高，因此，本文将该方法称为“增量式重构测量算法”。

如前所述，在得到了目标三维点云初始化重构结果后，可以实现相机相对目标位姿的实时测量。对于每一帧新采集的图像，由于其在观测初期阶段受重构精度的影响，其空间三维坐标会存在误差，该误差反过来又会引起摄像机相对位姿参数的计算出现误差。为此，通常将场景中的特征点三维坐标和摄像机位姿参数同时构建状态空间方程，利用图像序贯观测量进行滤波计算，同时对特征点坐标和位姿参数进行递推计算。本文沿用作者于2014年提出的递推深度参数模型[16]，并在此基础上，根据本文所涉及的目标三维点更新迭代过程应用需求，将该模型进行适应性改进如下：

(1)增量式重构测量算法中的状态更新方程

(7)

(8)

需要指出的是，在持续的观测过程中，无法保证能对特定点实现连续不间断的观测，因此针对状态量Zi(k)的选取，不能采用一成不变的目标特征点，而需要进行实时更新。本测量方案提出一种堆栈式迭代更新的处理方式，该方法利用特征点的反复观测，不断提高其深度特征的估计精度，此时可以认为，观测寿命越长的特征点，其估计精度也越高。因此，在状态方程中，将涉及的N个特征点按照观测寿命长短进行排序，当寿命最长的特征点的估计精度满足一定要求后，便可以用新观测到的新特征点去替换这些目标特征点，增加到系统状态方程之中，组成新的N个特征状态。被替换的目标特征点由于其观测寿命较长，其精度也已经满足要求，可以将其作为固化的三维世界坐标。而新加入的特征点，随着观测图像的增加，其观测寿命也不断提升，其深度估计精度也随之不断提高，当其达到一定的观测寿命后，也被新加入的特征点替换，成为固化的三维重构结果。

如图3所示，设定状态量中目标特征点数为N，即仅仅对N个特征点进行状态估计滤波处理；选取在前一阶段图像序列捆绑优化得到的N个三维特征点，作为状态量中的Zi(k)(i=1,2，…,N)；当寿命最长的m个观测点(即图3中最上面的m个特征点)的精度满足要求，将其作为固化的三维点加入三维模型，不再作为状态向量的元素，同时将新观测到的m个特征点，添加进入状态向量。m的确定原则为，使得每个新添入的三维点的观测次数不小于10次，因此有N/m≥10。

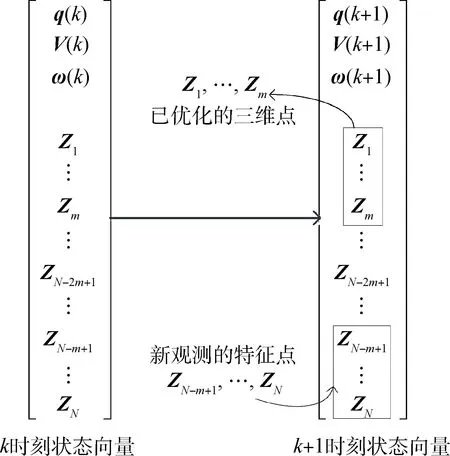
图3　状态向量更新示意Fig.3　Update of state vector

(2)增量式重构测量算法中的观测方程

(9)

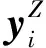
基于上述模型的相对位姿测量和新三维点的添加算法可以总结为以下步骤：

1)根据已恢复的三维点坐标，分别计算出相机的旋转矩阵RCkW和平移向量rWCW(k)，并根据上一时刻计算得到的旋转矩阵RCk-1W和平移向量rWCW(k-1)，并由此计算观测量y；

2)更新状态方程；

3)离散扩展卡尔曼滤波(EKF)；

4)相机位姿信息更新及新三维点世界坐标计算：

Pos(k)=Pos(k-1)+RCkWkVC(k)Δt

Pos(k)表示k时刻相机在世界坐标系中的位置。

3　试验验证

3.1空间航拍重构测量试验

本试验利用四旋翼无人飞行器搭载的摄像机对固定未知目标进行拍摄，并对所得到的图像进行重构和位姿测量试验。拍摄平台和试验场景如图4所示。

图4　试验场景示意Fig.4　Experiment scene

(1)试验描述

试验中，操作四旋翼无人飞行器，模拟飞行器从不同角度对固定目标进行拍摄的过程，以30帧/s的帧频进行拍摄，得到一组图片序列(视频)；基于该图片序列，进行了如下试验。

首先利用采集到的视频的前10s，每10帧选取一帧，选取出30帧图像，采用第2.1节的方法，重构出一系列目标的三维点坐标，这里得到了357个三维点，如图5所示。

图5　初始重构结果Fig.5　Initial reconstruction result

图5为初始重构的结果，由于仅仅通过单目视觉传感器，无法得到非合作目标的绝对尺度信息，因此图中的坐标无量纲。

随后，在上述三维点的基础上，采用第2.2节的方法，实现对相对位姿信息和新的特征点的同时优化估计，图6显示了几个时刻相机的位姿。试验数据的处理硬件平台为一台配置i7八核处理器的PC机，整个过程使用了2 160帧(72s视频)图像，总处理时间为223.56s，平均处理速度约为10帧/s。

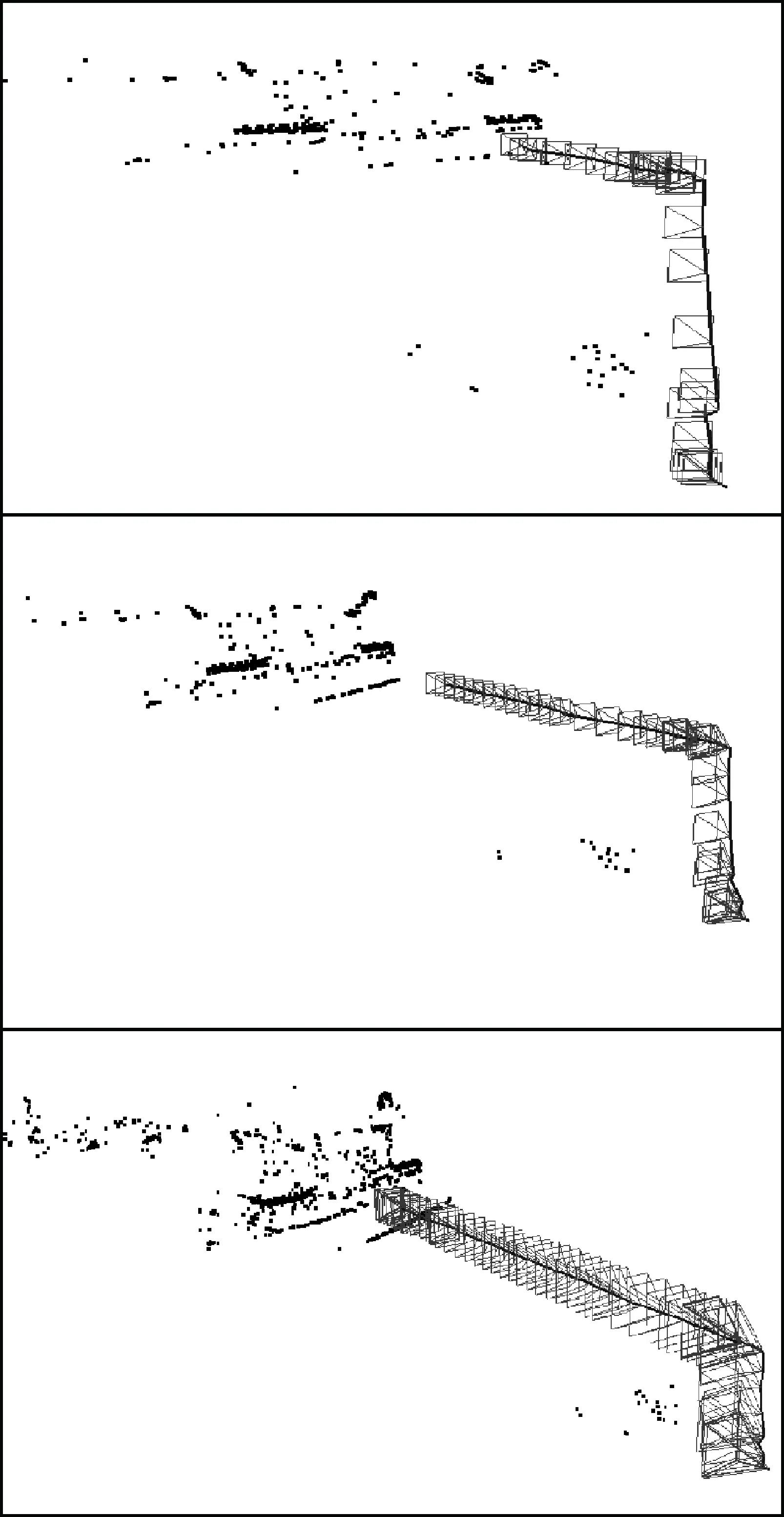
图6　相对测量结果Fig.6　Results of relative measurement

图6显示了测量过程中不同时刻相机的位姿，并标示出了相机光心的运动轨迹和相机的位姿，黑色点云标示了重构得到的一系列三维点。

(2)试验结果分析

由于无法得到相机在空间的位姿信息的真值，无法直接验证结果的正确性。为此，对重构测量的结果进行了重投影误差的分析。

1)单幅图像重投影误差分析。

在初始重构测量阶段使用的图片中，选取了第1帧、第15帧、第30帧3幅图像，进行重投影误差的统计分析。在此，选取精确重构点比例(在本文中，将重投影误差小于一个像素的点称为精确重构点)这一指标作为测量精度的衡量指标。对3幅图像的精确重构点比例随时间的变化进行了统计，结果如图7所示。

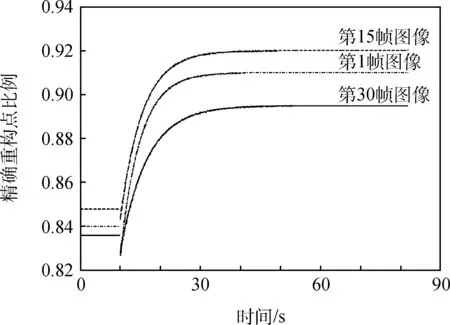
图7　单幅图像精确重构点比例变化Fig.7　Changing trend of the percentage of preciously reconstructed points

图7中，直线段是采用第2.1节的非线性约束的方法得到的试验结果，由于该过程不是一个增量式逐渐递推的过程，因此在此作为整体处理。其后是通过滤波处理得到的结果，由于在滤波初期，新观测的点的深度具有较大的不确定度，因此，精确重构点的比例有所下降；随着滤波器的收敛，精确重构点的比例逐渐提高；当一幅图中，所有特征点都成为固定的三维点，其精确重构点比例不再变化。可以看出，随着时间的推移，同一世界点被观测次数的增多，同一图像的精确重构点的比例逐渐增加。由于对于单幅图像，其对应的相机的位姿参数是确定的，重投影误差的大小仅取决于三维点坐标，精确重构点比例的增加表明重构得到的三维点坐标精度的提高。

2)重构测量最终结果重投影误差分析。

对测量完成后，得到的三维点坐标和相机的位姿进行全局的重投影误差分析，统计了测量过程中所使用的每帧图像的精确重构点的比例，结果如图8所示。

在全部使用的2 190幅图像中，精确重构点比例大于89%的图像有1 754幅，占所有图片的80%，表明该方法能够得到较为精确的重构测量结果。

图8　精确重构点比例分布Fig.8　A diagram of the percentage of precious reconstructed points

3.2公共数据集试验

第3.1节以空间小型测量平台为例，对所提方法的有效性进行了试验验证。然而，由于试验条件的限制，上述试验不能直接对单目视觉的测量精度进行评价。为此，本节借助于慕尼黑工大提供的单目SLAM公共数据集[17]，对算法的精度指标进行验证。重构测量结果如图9所示。

图9　公共数据集重构测量结果Fig.9　Results of reconstruction based on RGB-D SLAM dataset

图10对试验结果进行了描述。试验数据集采集过程中，摄像机的旋转和平移参数参考真值由惯性测量系统得到，由于试验时间较短，因此惯性测量结果可以用来作为参考。从试验结果可以看出，用本文所提出的方法，能够由单目摄像机采集的图像序列得到关于摄像机运动的姿态和位置参数。从图10中可以看出，姿态估计精度可以达到1°以内，而位置估计精度可以达到2cm以内。

图10　位姿测量结果Fig.10　Results of relative measure

5　结束语

针对非合作目标的相对位姿测量问题，提出了一种基于单目三维重构的实时测量方法。试验表明，该算法能够实现以10帧/s对非合作目标进行实时测量，姿态测量精度优于1°，能够满足针对非合作目标的高精度实时测量任务要求。由于仅仅通过单目视觉测量算法，无法得到真实世界的绝对尺度，因此，通过引入其他传感器信息，实现对非合作目标的具有绝对尺度的相对位姿测量，是下一步的研究方向。

References)

[1]崔乃刚，王平，郭继峰，等．空间在轨服务技术发展综述[J]．宇航学报，2007，28(4)：805-811．

CUI N G，WANG P，GUO J F，et al. A review of on-orbit servicing[J]. Journal of Astronautics，2007，28(4)： 805-811(in Chinese)．

[2]刘勇，徐鹏，徐世杰．航天器自主交会对接的视觉相对导航方法[J]．中国空间科学技术，2013，33(6)：33-40.

LIU Y， XU P， XU S J. Vision-based relative navigation for rendezvous and docking of spacecraft[J]. Chinese Space Science and Technology， 2013，12(6)：33-40(in Chinese).

[3]ZHOU J Y，ZHOU J P，JIANG Z C，et al．Investigation into pilot handling qualities in teleoperation rendezvous and docking with time delay[J]．Chinese Journal of Aeronautics，2012，25(4)：622-630．

[4]余慧杰，韩平畴. 双目视觉系统的测量误差分析[J].光学技术，2007，33(增刊)：157-159.

YU H J，HAN P C. Measuring errors analysis of binocular vision system[J]. Optical Technique， 2007，33(Suppl.)：157-159(in Chinese).

[5]NISTER D. An efficient solution to the five-point relative pose problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(6)：756-777.

[6]KLEIN G，MURRAY D. Improving the agility of keyframe-based SLAM[C]∥Proceeding of the 10th European Conference on Computer Vision，Marseille，France，October 12-18，2008.

[7]MOURAGNON E，LHUILLIER M，DHOME M. Generic and real-time structure from motion using local bundle adjustment[J]. Image and Vision Computing，2009，27(8)： 1178-1193.

[8]ENGELS C，STEWENIUS H. Bundle adjustment rules[C]∥Symposium of ISPRS Commission III Photogrammetric Computer Vision PCV， Bonn， Germany， September 20-22， 2006.

[9]TARDIF J，PAVLIDIS Y. Monocular visual odometry in urban environments using an omnidirectional camera[C]∥International Conference on Intelligent Robots and Systems， Nice， France， September 22-26，2008.

[10]杨东方，孙富春. 单目视觉系统自运动的滚动时域估计方法[J]. 模式识别与人工智能，2013，26(1)：76-82.

YANG D F，SUN F C. Moving horizon estimation of ego-motion in monocular visual systems[J]. Pattern Recognition and Artificial Intelligence，2013，26(1)： 76-82(in Chinese).

[11]FRAUNDORFER F，SCARAMUZZA D. A constricted bundle adjustment parameterization for relative scale estimation in visual odometry[C]∥International Conference on Robotics and Automation Anchorage Convention District，Anchorage，Alaska，USA，May 3-8，2010.

[12]王晓亮，邵晓巍，龚德仁. 空间非合作目标交会对接影像测量自适应处理[J]. 中国空间科学技术，2011，31(3)： 76-83.

WANG X L， SHAO X W， GONG D R. An adaptive approach to vision measurement for rendezvous and docking with non-cooperative target in space[J]. Chinese Space Science and Technology，2011，31(3)：76-83(in Chinese).

[13]徐文福，梁斌.基于立体视觉的航天器相对位姿测量方法与仿真研究[J]. 宇航学报，2009，30(4)：1421-1428.

XU W F，LIANG B. Stereo vision-based relative pose measurement method for spacecraft[J]. Journal of Astronautics，2009，30(4)：1421-1428(in Chinese).

[14]GERALD SCHWEIGHOFER，AXEL PINZ. Fast and globally convergent structure and motion estimation for general camera models[C]∥Proceedings of British Machine Vision Conference，Edinburgh，UK，September 4-7，2006.

[15]GROSSBERG M D，NAYAR S K. A general imaging model and a method for finding its parameters[C]∥ICCV，Vancouver，Canada，July 9-12，2001.

[16]YANG D F，LIU Z G. Recursive depth parametrization of monocular visual navigation：observability analysis and performance evaluation[J]. Information Sciences，2014，287：38-49.

[17]STURM J，ENGELHARD N，ENDRES F，et al. A benchmark for the evaluation of RGB-D SLAM systems[C]∥International Conference on Intelligent Robot Systems (IROS)，Vilamoura，Portugal，October 7-12，2012.

(编辑：车晓玲)

Aerial relative measurement based on monocular reconstruction for non-cooperation target

LI Yongfei，WANG Shicheng，YANG Dongfang*， SUN Dawei

Department of Control Engineering，Rocket Force University of Engineering，Xi′an 710025，China

A monocular vision-based relative position and attitude measurement algorithm was presented， which combined the reconstruction of targets with the measurement of relative positions and attitude for non-cooperation targets. Firstly， a series of points on the targets were reconstructed using the images obtained in the earlier measurement with a fast and globally convergent structure and motion estimation.Secondly， the relative position and attitude were calculated by using a Kalman filter based on recursive depth parametrization， in which new points observed from new images were recovered and added to the 3D point set to improve the accuracy and robustness of the measurement. Experiment result shows that the attitude measurement can achieve an accuracy higher than 1°,and the position measurement can achieve an accuracy higher than 2 cm， which indicates the high precision of the proposed algorithm.

target reconstruction；measurement for relative position and attitude；monocular vision；non-cooperation target

10.16708/j.cnki.1000-758X.2016.0057

2015-12-25；

2016-04-28；录用日期：2016-08-22；

时间：2016-09-2113:41:25

http:∥www.cnki.net/kcms/detail/11.1859.V.20160921.1341.006.html

国家自然科学基金(61403398)；总装预研基金(9140A01010413JB47005)

李永飞(1993-)，男，硕士研究生，lyfei314@163.com,研究方向为图像制导

杨东方(1985-)，男，博士，讲师，yangdf301@163.com，研究方向为图像制导

V448.2

A

http:∥zgkj.cast.cn

引用格式：李永飞，王仕成，杨东方，等. 基于单目三维重构的空间非合作目标相对测量[J].中国空间科学技术， 2016，36(5)：

48-56.LIYF，WANGSC，YANGDF，etal.Aerialrelativemeasurementbasedonmonocularreconstructionfornon-cooperationtarget[J].ChineseSpaceScienceandTechnology， 2016，36(5)：48-56(inChinese).