临近空间飞艇艇库外约束及稳定性分析

张泰华，姜鲁华，张冬辉，王立祥

1.中国科学院 光电研究院，北京 100094 2.中国科学院大学，北京 100049 3.中国科学院 高能物理研究所，北京 100049



临近空间飞艇艇库外约束及稳定性分析

张泰华1,2，姜鲁华1,3,*，张冬辉1,2，王立祥1,3

1.中国科学院 光电研究院，北京 100094 2.中国科学院大学，北京 100049 3.中国科学院 高能物理研究所，北京 100049

临近空间飞艇在发放前通常停放在艇库内，一旦离开艇库就不可避免地受到艇库外天气，尤其地面风的影响，不仅影响飞艇发放操作的快捷和安全，而且还事关飞行试验的成败。文章建立了大型飞艇在地面受两侧约束时的力学模型，采用动力学方法，分析了受到地面风作用时飞艇的姿态和约束拉力的变化，得到地面风起时和风速稳定后的解析解，评估了飞艇受到地面风作用时的稳定性和安全性。通过分析得到在两侧约束条件下飞艇对正向风和侧风的承受极限，为临近空间飞艇采用两侧约束方式的可行性提供了判据，也为今后发展临近空间飞艇发放技术提供借鉴。

临近空间飞艇；高空长航时演示验证飞艇；约束力；稳定性分析；发放技术

近些年来，临近空间因其大气环境、气象条件和高度等多方面突出的优势,使得在这一高度布防飞艇成为研究热点。人们一直尝试在临近空间高度部署飞艇，进行长期环境监测、通信中继和空中监视[1-2]。临近空间高度空气密度不到地面的十分之一，为使飞艇能够到达临近空间高度，飞艇长度一般都在百米量级，体积在万立方米或十多万立方米[3-6]。如此庞大的飞艇，一般有相应尺度的艇库保障。临近空间飞艇在地面时通常停放在艇库内，执行飞行任务时，要将飞艇从艇库移动至外面的发放场，确认飞艇状态正常后实施发放操作，飞艇升空。由于临近空间飞艇的尺度较大，在库外即使受到较小的地面风，尤其受到侧风时，飞艇迎风面积和阻力系数急剧增大，使得侧风阻力相当可观，给安全释放飞艇带来困难，严重时甚至可能损坏飞艇。因此，安全地释放临近空间飞艇，除了要求对地面风准确预报，并在飞艇出库过程尽可能慢速缓行外，还需要配置坚固可靠的地面设施，在移动过程中对飞艇采取科学合理、安全可靠的约束。

飞艇出库约束方式及发放操作直接决定了飞艇能否安全升空，是整个飞行试验成功的先决条件。各国在发展临近空间飞艇技术时，都将飞艇出库及发放控制方式作为探索的重点，并取得诸多成功经验[7]。自2003年起，美国空军开始发展临近空间概念模型，2005年，美国高空飞艇(High Altitude Airship，HAA)计划进入原型艇制造与演示验证阶段，2009年底完成了HAA缩比验证艇(High Altitude Long Endurance-Demonstrator，HALE-D)的研制，2011年7月27日进行了HALE-D的首飞试验[8-11]。

较之依靠锚泊塔牵引飞艇的传统方式，HALE-D飞艇采用两侧约束的方式，大大缩短了出库后的发放操作时间，为临近空间飞艇移动过程的约束及发放方式提供了极具参考价值的经验。但这种约束方式也存在缺陷，它使飞艇不具有风标效应，如果有地面风，尤其存在侧向分量的地面风时，只能依赖于两侧车辆约束飞艇，以抵抗地面风阻作用。本文分析在这种约束工况下飞艇受到地面风作用时的受力及其响应，分析结果可作为这种发放方式安全性评估的判据。

1　飞艇出库两侧约束方式

HALE-D飞艇在出库过程中，两侧各用2辆辅助车辆约束飞艇，飞艇腹部有1辆随动车辆，通过这5辆辅助车辆将飞艇牵引至发放场地，然后实施发放。其中，HALE-D飞艇出库过程中的状态如图1所示[12]。

图1　HALE-D 出库照片Fig.1　HALE-D leaves its hangar

为使问题具有普遍意义，选取传统飞艇艇型，飞艇后部装有夹角成120°的3个尾翼。在将飞艇移出艇库直至到达发放场的过程中，两侧由4辆车约束，约束车辆通过拉绳与艇身上的连接袢连接，飞艇腹部有一辆托车提供支撑，托车能够向任意方向移动，飞艇在出库过程中的约束情况如图2所示。

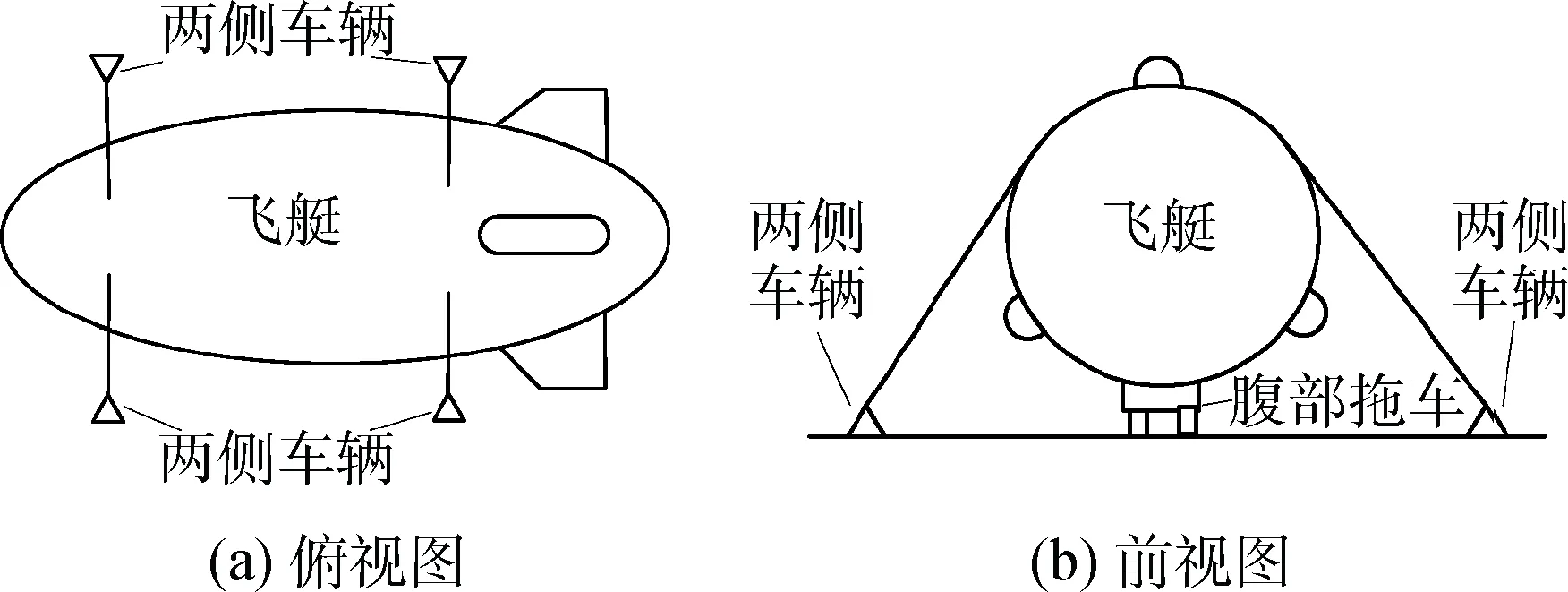
图2　飞艇约束示意Fig.2　The diagram of airship constraint

一般而言，两侧约束车辆只能沿规定方向行驶，约束飞艇只能在一定范围内活动，腹部托车只起支撑作用，可随飞艇在水平面内自由摆动。在这种约束条件下，如果艇库外无风或接近静风，这些设备将控制飞艇安全到达发放场地，一旦出现突风，两侧车辆与飞艇之间的拉绳以及艇身上的连接袢受力如何？飞艇姿态将会有怎样的变化？受到地面风作用时，飞艇的稳定性如何？在艇库外，飞艇能承受的地面风极值有多大？本文将通过分析和计算，解决这些问题。

2　受力及稳定性分析

在飞艇从艇库转移至发放场的过程中，地面风的大小和方向往往都是非定常的。为便于分析，将任意方向的地面风按照风向与飞艇轴向的夹角分解为正向和侧向两个分量，将风向与飞艇航向平行的称作正向风，将风向与飞艇航向垂直的称作侧风。

在不影响正确分析并力求尽可能得到精确解的前提下，作以下近似假设：艇体为刚体，在艇体偏转过程中，约束飞艇的两侧车辆相对位置保持不变；各拉绳为拉力绳，形变不计；艇体受到侧风作用偏移时的横滚不计，飞艇保持仰角不变。

建立三维坐标系Oxyz，原点为艇头，Ox轴为飞艇纵轴，Oy轴垂直Oxz平面，三轴符合右手法则。

2.1正向风

正向风是飞艇在出库移动过程中常见的风向，即使在静风环境下进行出库操作，因飞艇移动过程中相对气流存在相对速度，导致正向风的客观存在，这往往限制了大型飞艇在出库移动过程中必须匀速缓慢前行。

当飞艇受到地面正向风时，两侧车辆拉绳偏移，拉绳拉力的水平分量平衡风阻，此时的受力如图3所示。

根据牛顿第二定律，Oxy平面内，有：

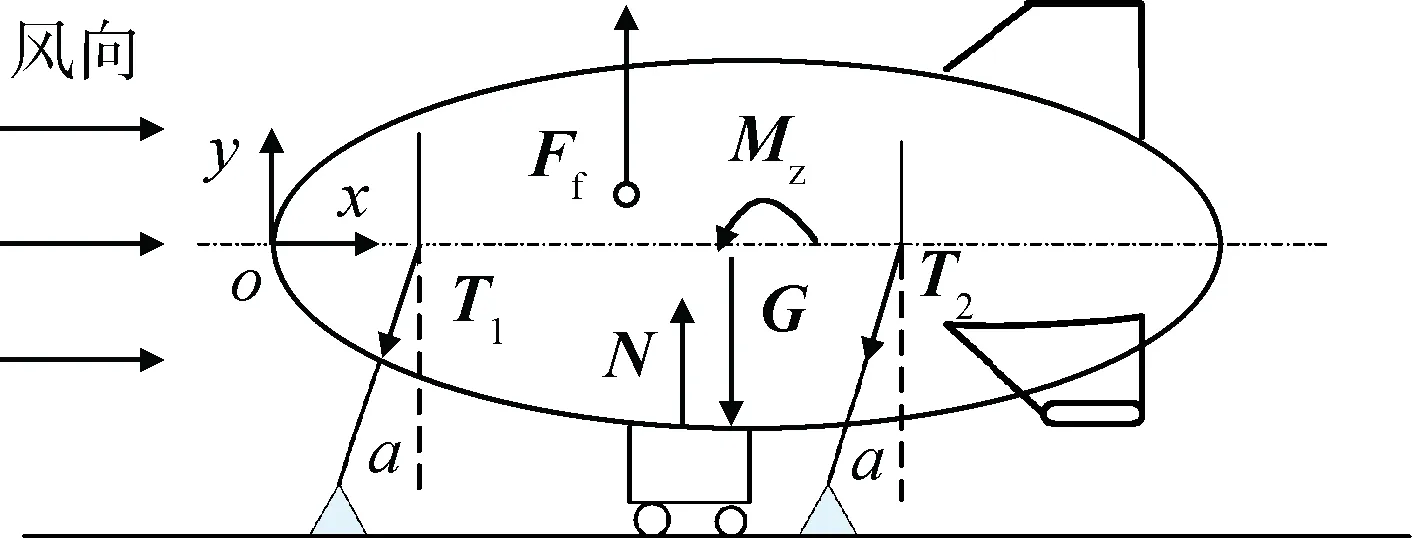
图3　正向风时飞艇受力示意Fig.3　Force diagram for airship in forward wind

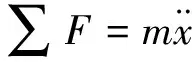
(1)

式中：m为飞艇系统总质量。水平合力：

∑F=Fd(t)-[T1(t)+T2(t)]sina=

(2)

式中：V为飞艇体积；Cd为飞艇气动阻力系数；v0为风速；v为飞艇移动速度；T1(t)和T2(t)分别前后拉绳两侧合拉力的Oxy平面内的分量；为两侧约束拉绳在Oxy平面内的投影长度；Fd是飞艇受到的空气阻力。将式(2)代入式(1)得：

[T1(t)+T2(t)]x/l-

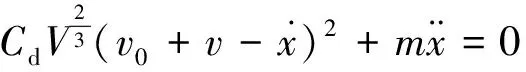
(3)

垂直方向上，根据力和力矩平衡，有：

(4)

(5)

式中：a为拉绳偏移角度；Fb和Xb分别为飞艇浮力和浮心横坐标值；G和XG分别为飞艇总重和重心横坐标值；N(t)和XN分别为腹部托车支撑力和支撑点横坐标值；Xi为第i对拉袢横坐标值。而：

式中：Md0为飞艇初始气动力矩。代入式(5)，有

(6)

一般情况下，腹部托车在静风状态下受到的垂直作用力很小，当飞艇受到地面风作用，两侧拉绳摆动而使艇身高度降低，飞艇与地面之间的空间减小，腹部托车提供支撑确保飞艇与地面之间有足够的安全距离。在飞艇垂直方向变形较小的情况下，支撑力可近似为与位移成正比[14]，据此可以得到腹部托车支撑力与各拉绳投影长度之间的关系为：

(7)

其中，比例系数k与飞艇轮廓及艇囊压差有关。

根据边界条件，可求得T1(t)、T2(t)和N(t)，以及它们的极大值T1max、T2max和Nmax。有两个特殊情况：

1)地面风起瞬间。此时，边界条件有：

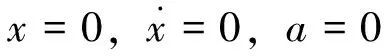
(8)

2)地面风稳定作用时。此时，系统将处于稳定状态，边界条件为：

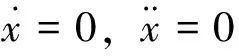
(9)

代入式(3)、式(4)、式(6)和式(7)，可求得稳定状态下的T1、T2和N。

2.2侧风

飞艇在艇库外受到与艇身不平行的地面风，或是在发放场等待发放过程中受到地面风作用，都会受到与艇身航向垂直的侧风，侧风起时，飞艇由静转动，系统巨大的惯性使得响应渐变而缓慢，艇身和约束部件闻风运动，姿态和受力发生复杂的变化，甚至会导致系统破坏。

飞艇受到侧风时，艇体带动腹部托车随风摆动，飞艇受力示意如图4所示。

图4中，aij为飞艇轴向受侧风作用的偏转角度，βij为拉绳因飞艇偏转而形成的夹角，Tij为侧拉袢拉力，α为飞艇偏航角。飞艇匀速移动过程处于平衡状态，移动速度产生的风阻与前进方向平行，无侧向风力分量，在此不再单独考虑移动速度。

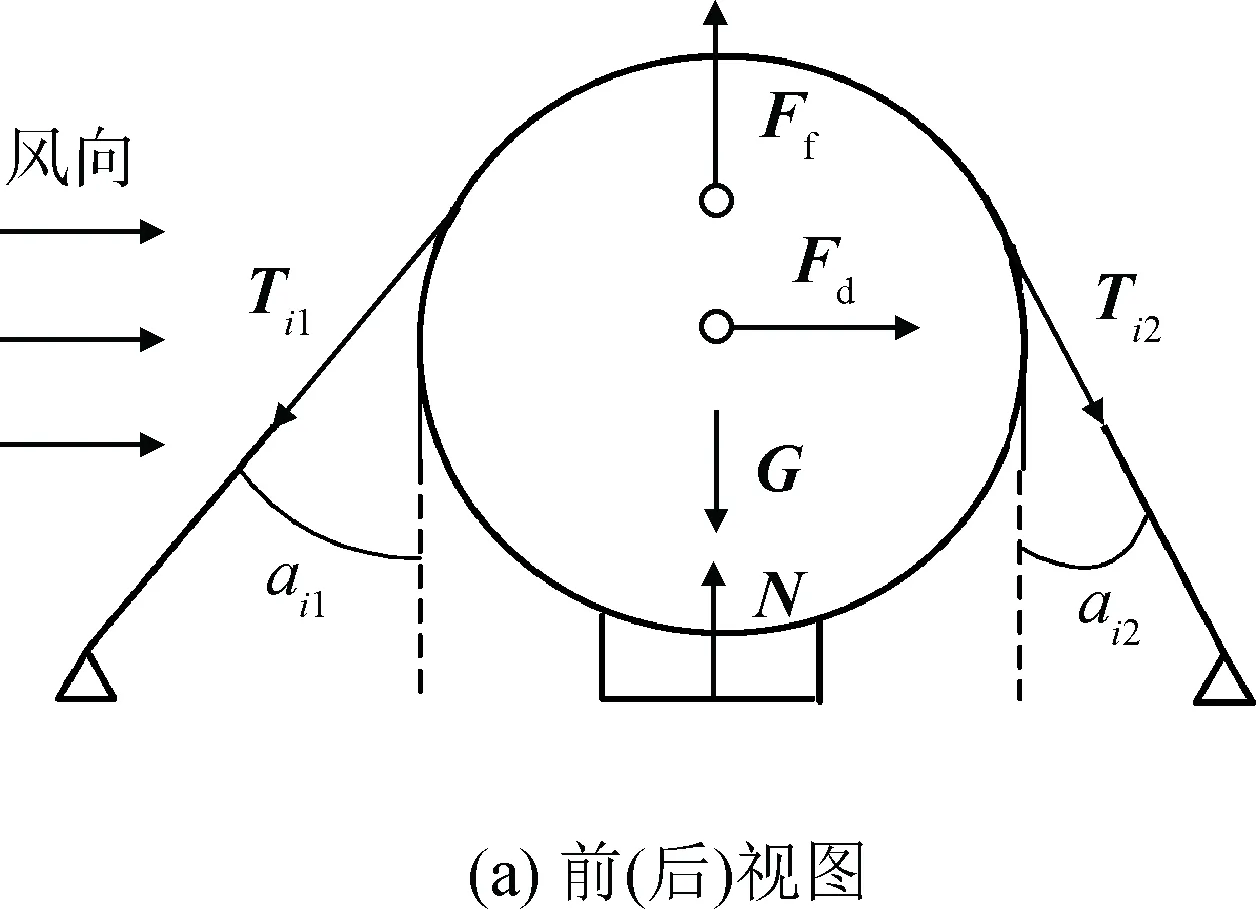
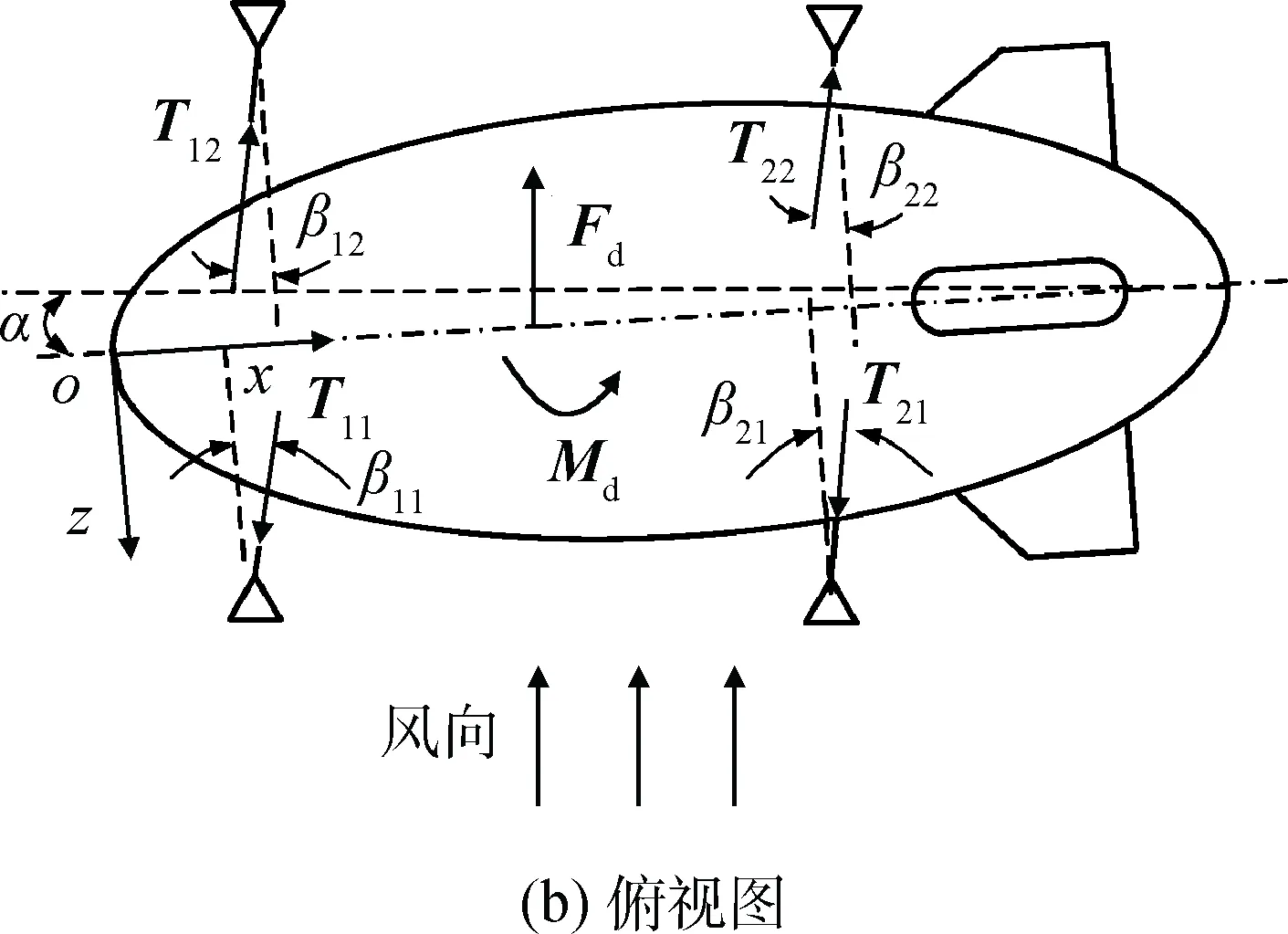
图4　侧风作用时飞艇受力示意Fig.4　Force diagram for airship in crosswind

根据牛顿第二定律，在Oxz平面内，有：

(10)

(11)

式中：f为中间托车与地面之间的摩擦力；Si为第i对艇上拉袢点之间间距的一半。其中：

(12)

式中：μ为摩擦系数。结合式(7)，根据前后拉袢的几何关系，可得：

N(t)=kΔy=

(13)

式中：L为两侧拉绳长度。在Oxy平面内，由于飞艇受约束仰角保持不变，有：

(14)

(15)

假设飞艇不滚转，各载荷对艇体中心合力矩为0，有：

R0T11(t)cos(a11-a0)cosβ11=

(16)

R0T21(t)cos(a21-a0)cosβ21=

(17)

式中：R0为拉袢点飞艇半径；a0为两侧拉绳与艇身初始夹角。根据边界条件，可求得Tij、aij、βij和N(t)，以及它们的极大值。

在以下几种工况：

1)地面风突起瞬间。此时，

(18)

边界条件：

(19)

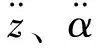
2) 地面风稳定时。此时，系统将处于稳定状态，边界条件为：

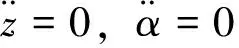
(20)

式(10)、式(11)、式(14)和式(15)简化为：

(21)

(22)

(23)

(24)

受到侧风作用飞艇整体发生偏航，此时两侧约束车辆相对位置保持不变，各拉绳夹角可以用飞艇横向偏移z和偏航角α表述，即：

(25)

式中：i=1,2;j=1,2。

在图4(b)所示平面内，给定广义坐标下的虚位移δα，各力在虚位移下所做的虚功为：

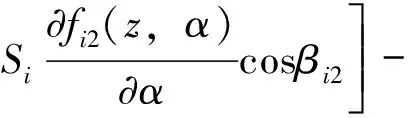
(26)

根据虚位移原理：

(27)

因为δα是任意微小量，则δα≠0，于是

(28)

根据上述方程，即可求得飞艇受到侧风稳定时的偏航角α。

通过式(21)～式(24)，可求得地面风突起时的Tij、aij、βij和N。

当飞艇在艇库外受到侧风时，飞艇因状态变化或连接受力过大而存在失控或结构破坏的风险。

飞艇在这种两侧约束方式下，艇库外承受侧风安全范围取决于以下两个因素：

1)飞艇偏移超出安全范围。飞艇在艇库外受到侧向分量的地面风作用，飞艇姿态会发生变化，在上述求解过程中，如果所求得的拉绳夹角出现aij≤0的情况，则飞艇受到过大的侧风，飞艇偏离两侧约束区域，在下风向的一侧拉绳将缠绕艇身，另一侧拉绳与艇身夹角过大，存在撕裂拉袢的风险，如图5所示。这种情况非常危险，是不允许出现的工况。在求解过程中，如果出现这种情况，对应的风速超过了两侧约束方式所能允许的上限。

2)飞艇连接安全性。通过上面的计算，可以求得各拉绳Tijmax，以及腹部托车的支撑力Nmax，据此可以得到两侧拉绳及其与艇身上连接袢的连接受力最大值，以及腹部托车承受载荷及其与艇体连接的最大值，据此，根据拉绳破断强度和托车承重极限评估地面风作用时承受侧风作用极限。

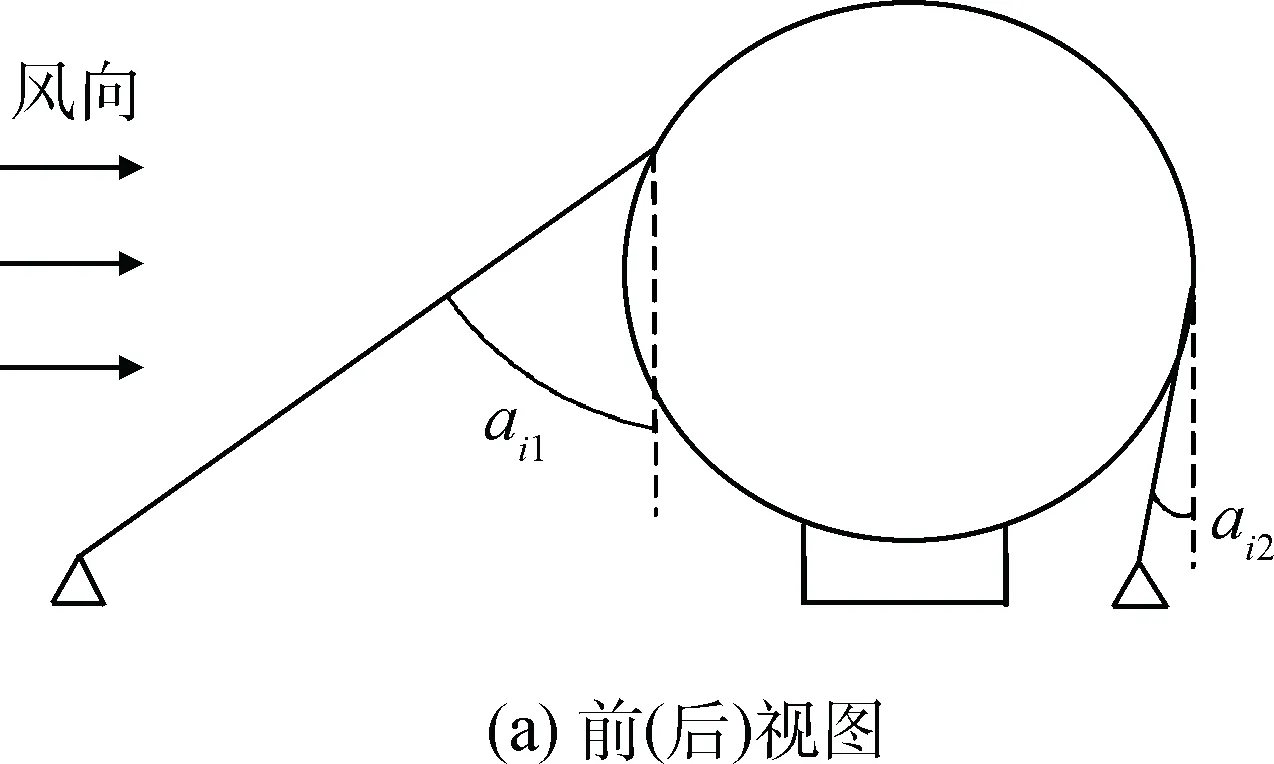
图5　受过大侧风作用时飞艇的偏移示意Fig.5　Deflection diagram for airship in excessive crosswind

3　算例

为使算例具有普遍意义，计算模型采用Skyship艇型，假设飞艇艇长100 m，两侧车辆拉绳初始夹角为a0=40°，根据Skyship艇型[15-16]，主要参数包括：最大直径Dmax=25.75 m，体积V=32 460 m3，几何中心距离艇头49.4 m，G=31.8 kN，Fb=1.1G=34.98 kN，Xb=43.82 m，XG=44.73 m，X1=9.4 m，X2=69.4 m，XN=44.93 m，R0=9.47 m，气动阻力系数通过软件计算得到[16]。

当该飞艇移动出艇库或在艇库外发放前受到地面风作用时，利用上述分析，求解飞艇的响应及各拉绳拉力、拉绳夹角等参数的变化情况，进而验证采用这种库外约束方式的安全性能，为同量级飞艇库外约束方式提供参考。

3.1正向风作用

利用上述计算和分析，得到正向风作用时拉绳夹角及腹部托车、两侧拉绳拉力变化曲线分别如图6～图8所示。

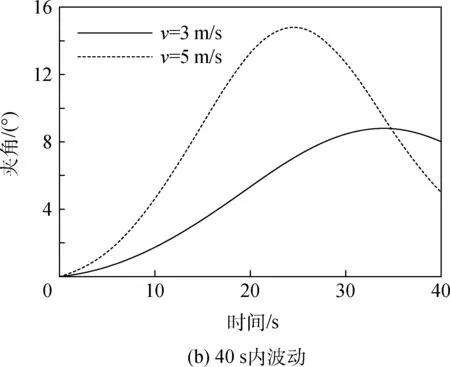
图6　不同正向风作用时拉绳夹角变化Fig.6　Rope angle variations in different forward wind

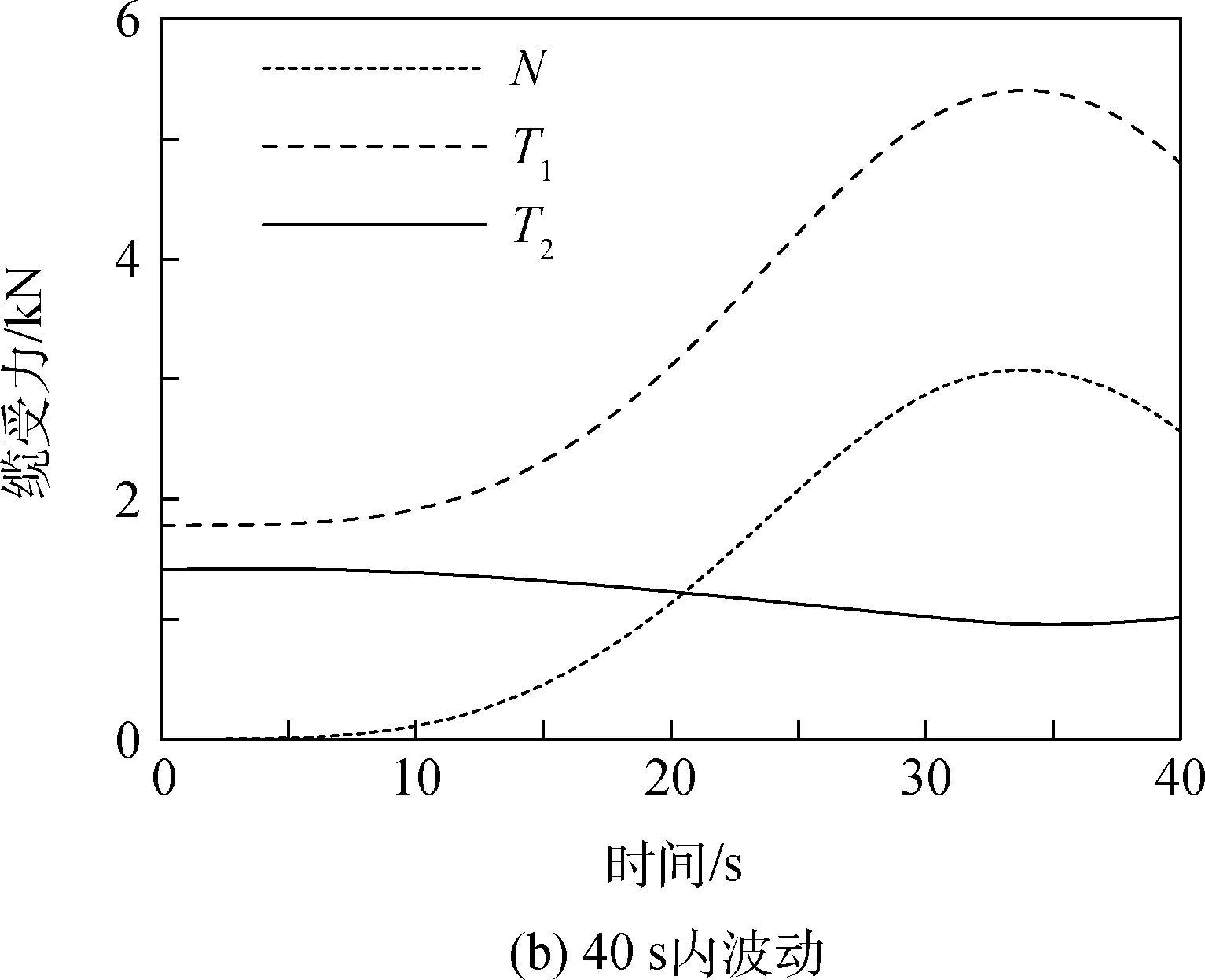
图 7　地面风3 m/s腹部托车及前后拉绳拉力变化Fig.7　Tension variations of bottom vehicle and ropes in forward wind (3 m/s)

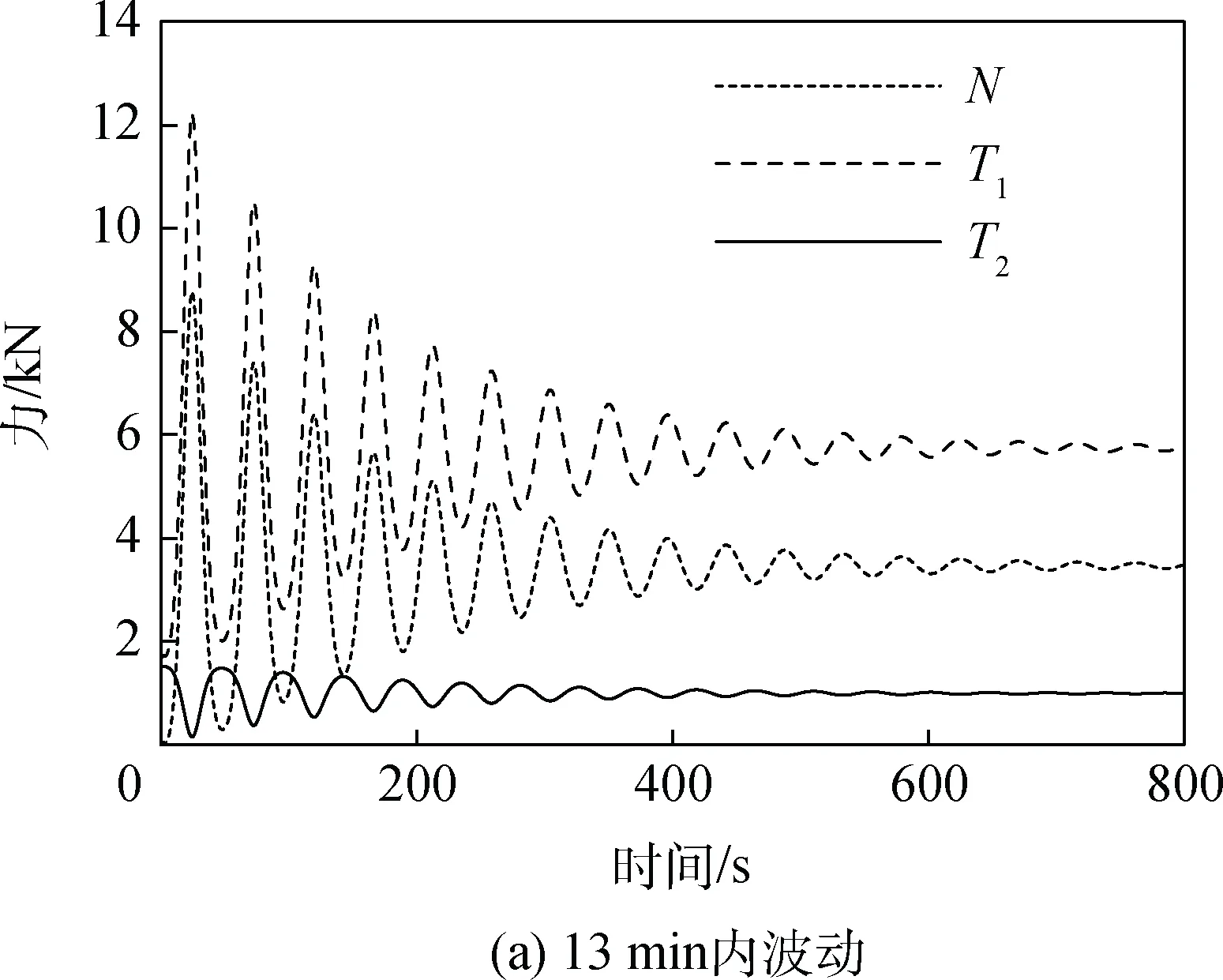
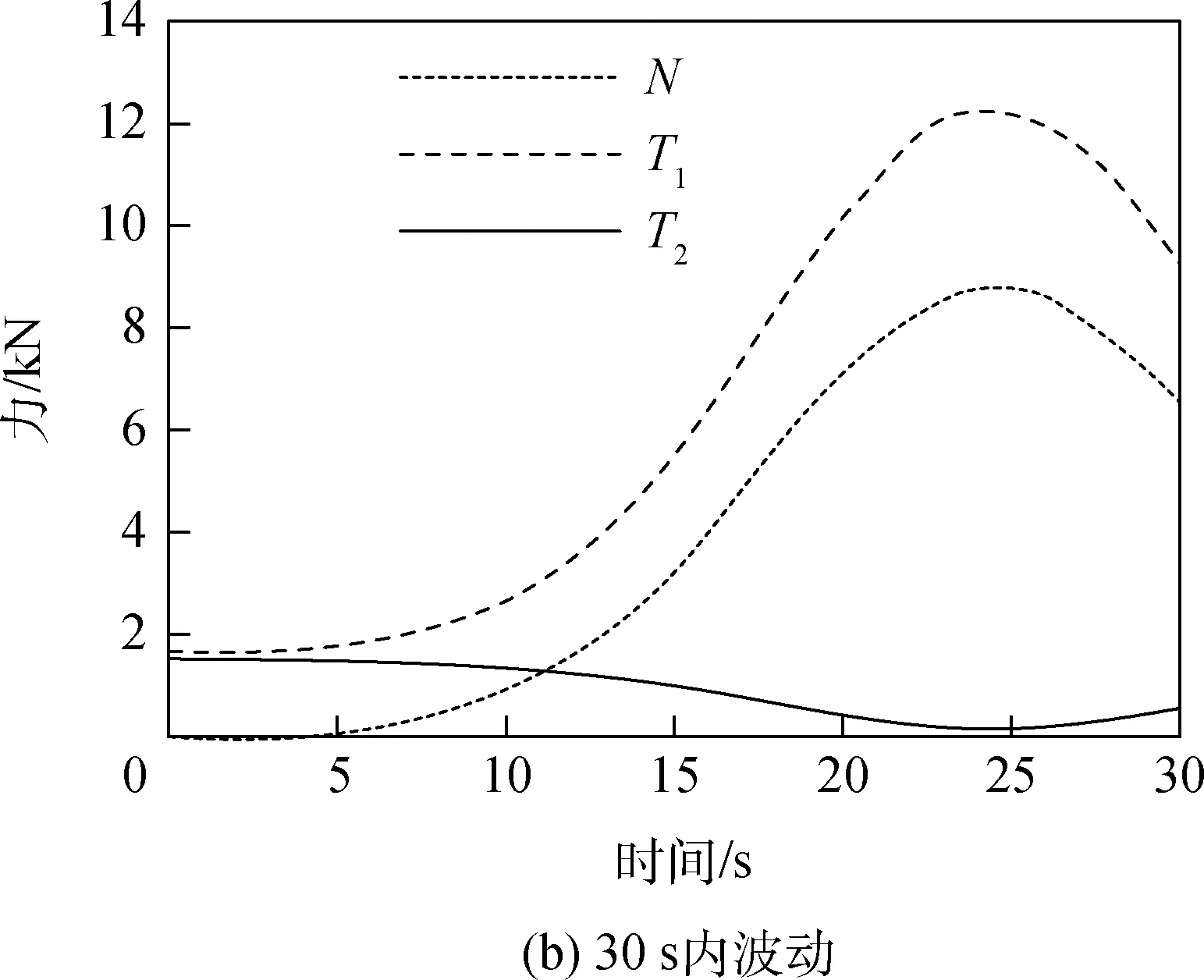
图8　地面风5 m/s腹部托车及前后拉绳拉力变化Fig.8　Tension variations of bottom vehicle and ropes in forward wind (5 m/s)

初始状态和稳定状态下，数据如表1所示。

从计算结果可知，该飞艇受到5 m/s正向突风时，其前拉袢最大拉力垂直分量为12.223 kN，每侧拉绳垂直拉力分量为6.11 kN，如果拉绳与垂直夹角为40°，则拉绳拉力为7.98 kN，取2倍安全系数，拉力为15.98 kN，对于艇上拉袢而言，显然比较危险，应改变拉绳与艇囊之间的连接方式，采用多袢集束的方式，或采用其他约束飞艇的方式。

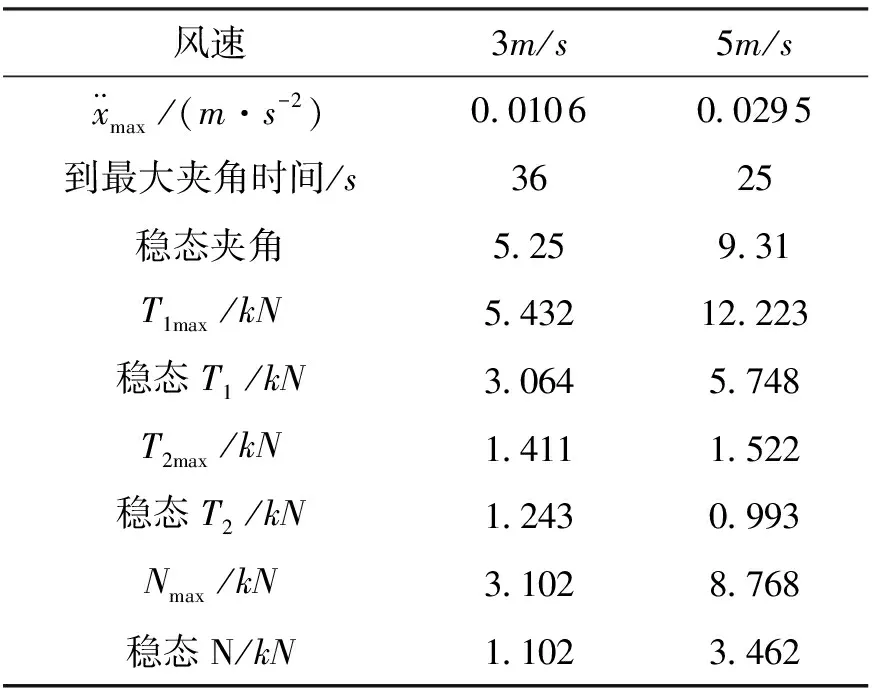
表1　不同正向风时T和N计算值

3.2侧风作用

根据以上公式，分析飞艇在艇库外受到不同大小的侧风作用时系统的响应，取侧风分别为1 m/s、3 m/s和5 m/s，得到飞艇受到侧风作用时出现的最大(小)值如表2所示。经过一定时间的稳定，系统将处于平衡状态，得到稳定状态系统的参数如表3所示。

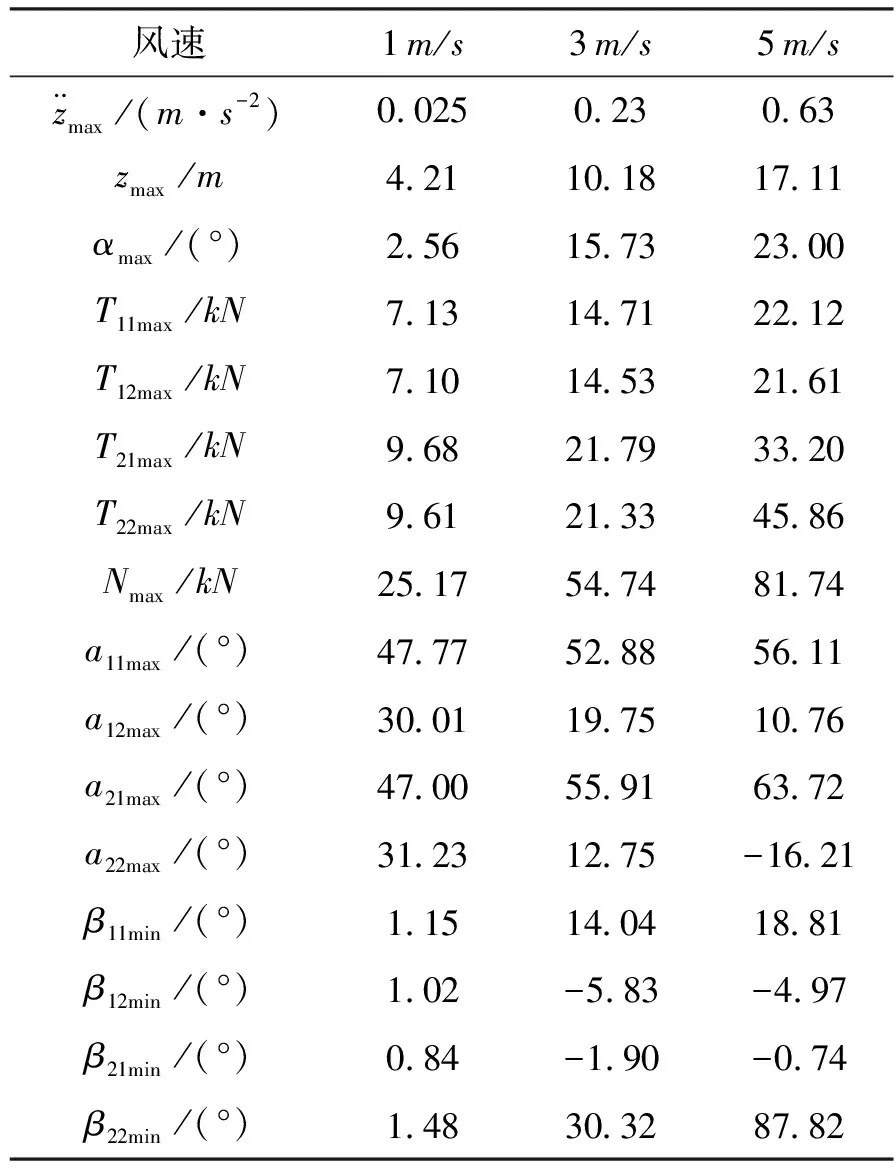
表2　不同侧风作用时各参数极大(小)值

以3 m/s的侧风为例，分别得到Tij、aij、βij，以及飞艇侧滑距离z和偏航角α随时间变化曲线，分别如图9～图12所示。

图9　侧风3m/s时Tij和N随时间变化曲线Fig.9　Fluctuations ofTij and N in 3 m/s crosswind

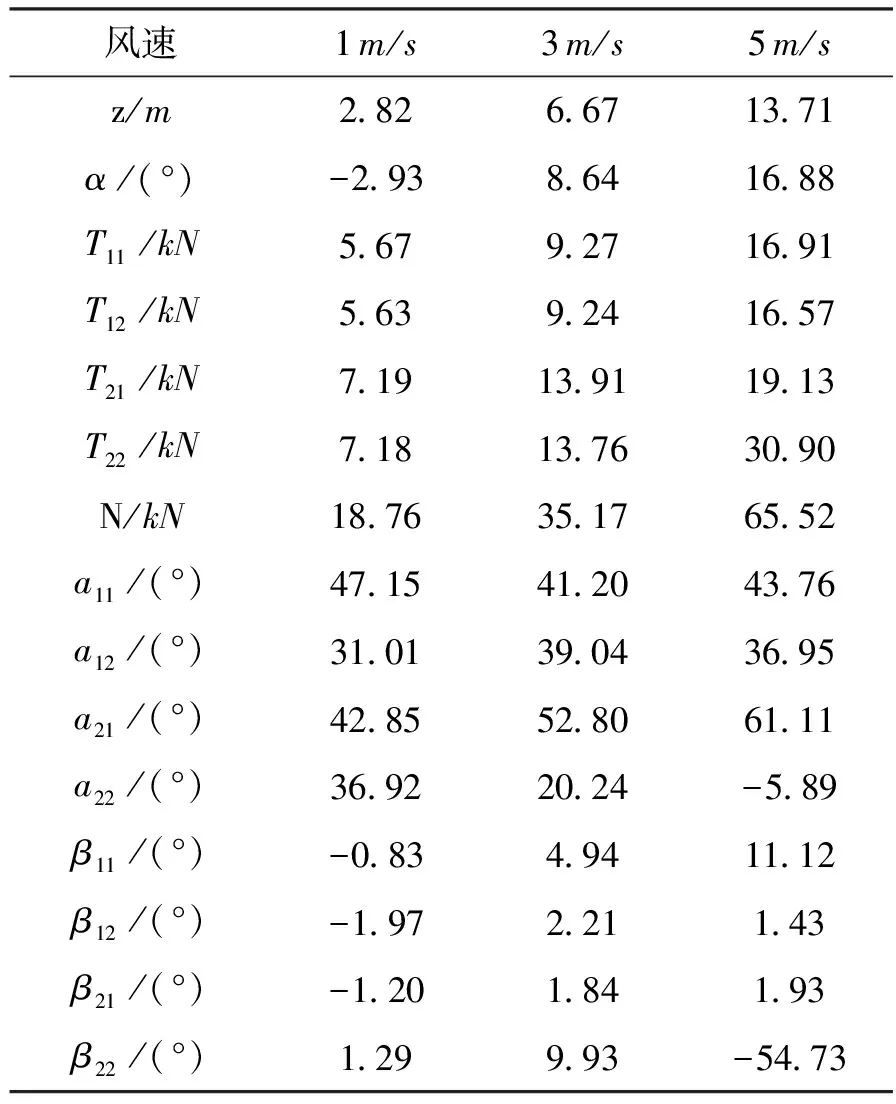
风速1m/s3m/s5m/sz/m2826671371α/(°)-2938641688T11/kN5679271691T12/kN5639241657T21/kN71913911913T22/kN71813763090N/kN187635176552a11/(°)471541204376a12/(°)310139043695a21/(°)428552806111a22/(°)36922024-589β11/(°)-0834941112β12/(°)-197221143β21/(°)-120184193β22/(°)129993-5473

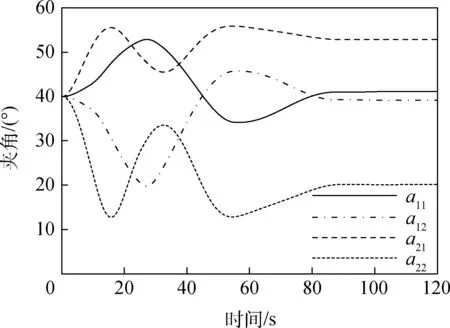
图10　侧风3 m/s时拉绳夹角aij变化Fig.10　Fluctuation of aij in 3 m/s crosswind

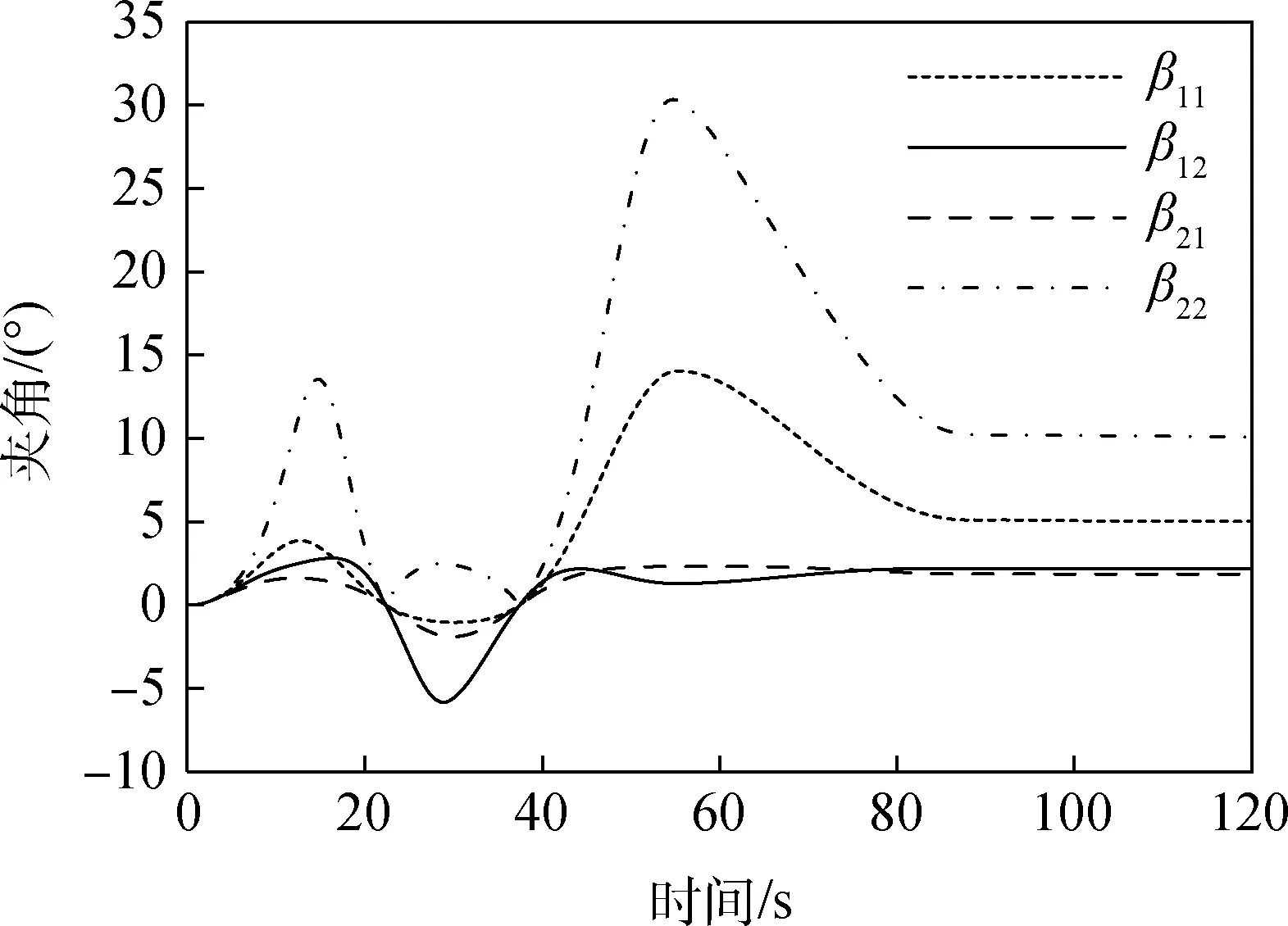
图11　侧风3 m/s时βij 变化Fig.11　Fluctuation of βij in the 3 m/s crosswind

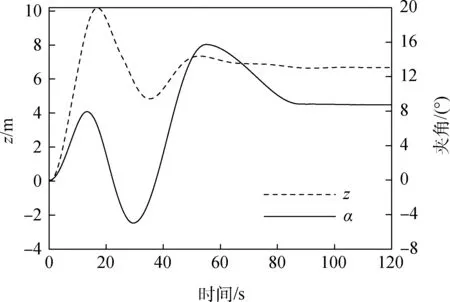
图12　侧风3 m/s时飞艇侧滑z和偏航角α变化Fig.12　Fuctuations of z and α in 3 m/s crosswind

受到侧风作用，飞艇偏移最大时如图13所示。

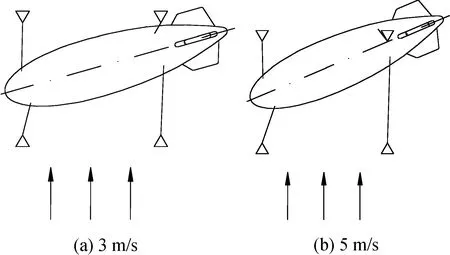
图13　侧风作用飞艇最大偏移俯视图Fig.13　Maximum offset of airship in crosswind

从上述分析可知，当侧风达到5 m/s时，a22<0，此时飞艇已偏转至侧面约束车辆上方，已无法有效地操控飞艇，说明采用这种约束形式，当受到地面风侧向分量大于5m/s时，已超过了可以承受的上限。在飞艇受侧风偏移过程中，两侧拉绳最大拉力达到了45.86 kN，这一量级对于艇体连接处拉袢而言，是非常严峻的考验。

在进行计算分析过程中，动力学模型拉绳和艇体简化假设导致了拉力极值急剧增大，其极值与实际有较大偏差，实际中，无论是拉绳、拉袢，还是飞艇本身，都是弹性体，系统本身也会吸收和消耗能量，更精确的计算将在后续工作中进一步深入研究。

4　结束语

通过以上分析，可以得到以下结论：

1)采用两侧对称约束的连接方式，一旦出现突风，两侧车辆与飞艇之间的拉绳以及艇身上的连接袢受力将急剧增大。飞艇在艇库外受到正向突风时，前面两侧拉绳拉力急剧增大，后面两侧拉绳拉力增大幅度较小，甚至有减小趋势，风速越大，飞艇偏移距离和角度越大，前面两侧拉绳拉力越大，飞艇姿态保持稳定。

2)飞艇在艇库外承受侧风比正向风更危险，飞艇的位移和方向都发生了较大的变化，艇身上各连接处的承力将急剧增大，飞艇发生偏航和水平漂移，姿态不稳定，随着风速进一步增大，飞艇将漂移出约束车辆可控区域，进而导致约束失控。在艇库外，长度为100 m的临近空间飞艇，其承受侧风极限不超过5 m/s。

3)飞艇转移出库过程是较为危险的阶段，应提高气象预报准确性，尽可能减小或避免在出库过程中受到侧风作用，或制定科学合理的措施，对飞艇的约束方式加以完善，减小飞艇受到侧风作用时连接点的承力极值。

References)

[1]欧阳晋,屈卫东,席裕庚. 平流层平台的发展及其自主控制关键技术[J]. 工业仪表与自动化装置, 2014(1): 64-67.

OUYANG J, QU W D, XI Y G. The development of a stratospheric platform and its automonous control technology[J]. Industrial Instrumentation & Automation 2014(1): 64-67 (in Chinese).

[2]LIN L, IGOR P. A review of airship structural research and development[J]. Progress in Aerospace Sciences，2009(45)：83-96.

[3]JAMISONL J, SOMMER G S,PORCHE I R. High-altitude airships for the future force army[R]. OMB No. 0704-0188，ISBN 0-8330-3759-5,2005.

[4]LEE M, SMITH S, ANDROULAKAKIS S. The high altitude lighter than air airship efforts at the US army space and missile defense command/army forces strategic command[C]∥18th AIAA Lighter-Than-Air Systems Technology Conference, 4-7 May，2009, Seattle,Washington. AIAA: 2009-2852.

[5]CASEY S, ALESSANDRO C, PIER M. Airship research and development in the areas of design, structures, dynamics and energy systems[J]. International Journal of Aeronautical & Space Science,2012,13(2): 170-187.

[6]WILSON J R. A new era for airships[J]. Aerospace America,2004;42(5): 27-31.

[7]BLACKINGTON E. United States air force, schriever air force base [R]. Near Space Maneuvering Vehicle, AIAA-LA Section/SSTC 2003-6005, 2003.

[8]HILLSDON R H. Launching of high altitude airships[P]. USA. PCT/GB00/00386,17 August,2000.

[9]EDWARD B, PHIL T D. The paradigm shift to effects-based space: near-space as a combat space effects enabler[R]. Airpower Research Institute, College of Aerospace Doctrine, Research and Education, Air University, 2005.

[10]SMITH I S, The HiSentinel airship[C]∥7th AIAA Aviation Technology, Integration and Operations Conference，18-20 September,2007.Belfast, Northern Ireland. AIAA: 2007-7748.

[11]United States Government Accountability Office. Future aerostat and airship investment decisions drive oversight and coordination needs[R]. October,2012. GAO-13-81 Defense Acquisitions: 34-35.

[12]Lockheed Martin. Highaltitude airship[EB/OL].(2013-01-01) [2015-01-09].http:∥www.lockheedmartin.com/us/products/lighter-than-air-vehicles.

[13]KHOURY G, GILLETT J. Airship technology[M]. Cambridge: Cambridge University Press; 1999: 24-25.

[14]ZHANG T H, YANG Y C, GAO H，et al．Load-carrying ability and application of composite materials air cushion in the Aerostat[J]. Applied Mechanics and Materials,2014,482: 302-310.

[15]KHOURY G A,GILLETT J D.Airship technology[M].Cambridge: Cambridge University Press, 1999:33-42.

[16]CUI Y X, YANG Y C, ZHOU J H, et al. Numerical aerodynamic investigations on stratospheric airships of different tail configurations[C]∥IEEE Aerospace Conference.Montana,March 7-14, 2015.

(编辑：高珍)

Constraint and stability analysis of near space airship outside hangar

ZHANG Taihua1,2,JIANG Luhua1,3,*,ZHANG Donghui1,2,WANG Lixiang1,3

1.Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China 2.University of Chinese Academy of Science, Beijing 100049, China 3.Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China

Typically, the near space airship parks in the hangar before launch. As soon as near space airship leaves its hangar it will be affected by the weather and particularly by the wind,which not only affect the rapidity and security of the airship operation, but also relate to the success of the flight test.A mechanical model was established when an airship was outside its hangar with both sides restricted. The variations of airship yaw and rope tension were analyzed by using dynamic method. The analytical solution was obtained at the beginning and stable state of the wind, then, the stability and safety of an airship were also evaluated. The ultimate bearings of forward wind and crosswind on an airship outside the hangar were proposed.The result quantifies the indicators of meteorological conditions, and provides references of scientific and rational methods for the launch technology of near space airship in the future.

near space airship；high altitude long endurance-demonstrator；force of constraint；stability analysis；launch technology

10.16708/j.cnki.1000-758X.2016.0060

2016-03-03；

2016-04-07；录用日期：2016-08-22；

时间：2016-09-2113:41:35

http:∥www.cnki.net/kcms/detail/11.1859.V.20160921.1341.010.html

高分辨率对地观测系统重大专项(飞艇总体技术研究与试验)；中科院知识创新重大项目(平流层试验飞艇研制与集成演示)

张泰华(1982-)，男，博士研究生，zth@aoe.ac.cn,研究方向为浮空器结构设计

姜鲁华(1956-)，男，研究员，jianglh@ihep.ac.cn，研究方向为浮空器总体设计

V274

A

http:∥zgkj.cast.cn

引用格式：张泰华,姜鲁华,张冬辉,等. 临近空间飞艇艇库外约束及稳定性分析[J].中国空间科学技术, 2016,36(5)：

72-80.ZHANGTH,JIANGLH,ZHANGDH,etal.Constraintandstabilityanalysisofnearspaceairshipoutsidehangar[J].ChineseSpaceScienceandTechnology, 2016,36(5)：72-80(inChinese).