一种基于多终端约束的最优制导方法

李超兵，王晋麟，李海

北京航天自动控制研究所，北京 100854



一种基于多终端约束的最优制导方法

李超兵*，王晋麟，李海

北京航天自动控制研究所，北京 100854

在航天器主发动机推力大小不可调的前提下，针对5个终端约束下传统迭代制导小角度修正假设的不足，对一种基于多终端约束的最优制导方法进行了研究。在入轨点轨道坐标系下建立航天器的最优控制模型，对横截条件方程组直接进行迭代求解获得制导角度指令，在此基础上，通过对开关机点进行优化以减小未被满足的终端位置约束的影响；进一步，推导了地心惯性系下等效的5个终端约束，并通过引入权重因子来提高制导方程数值求解的精度。标准条件下的仿真结果表明，所提制导方法与传统迭代制导相比，未被满足的终端位置约束精度提高了159.535 5m，而其余5个终端约束几乎不受影响；蒙特卡罗打靶仿真结果表明，所提制导方法对航天器初始位置和速度偏差具有一定的适用性。

航天器变轨；迭代制导；最优控制；坐标转换；开关机点优化；权重调整

航天器在空间中为完成预定的任务，需要通过制导来完成不同轨道之间的转移。由于航天器的发动机推力大小有限，因此通常需要选取合适的发动机开关机点以完成制导[1-4]。

传统的制导方法包括摄动制导、迭代制导等，由于摄动制导存在射前装订数据复杂，入轨精度差等缺点，为进一步提高制导精度，以迭代制导代表的自适应制导方案逐渐为许多航天器所采纳[5]。

迭代制导最初应用于美国的土星五号运载器上[6]，国内韩祝斋[7]在最优控制原理的框架下对迭代制导的方程进行了描述；陈新民和余梦伦[8]推导了多级迭代制导方程，茹家欣[9]给出了一种更为简洁的迭代制导方法。

传统的迭代制导针对航天器主发动机推力大小不可调的情况，通常考虑5个终端约束，包括两个方向的位置约束和3个方向的速度约束，首先求解满足速度约束的控制角，然后在位置约束引起的角度变化为小量的假设下对控制角进行修正[6-9]，但在某些变轨情形下，这一假设不再成立，此时传统迭代制导无法适用。

现有文献对迭代制导的改进包括控制对象模型复杂性和利用最优控制原理推导的方程形式等方面。文献[10]考虑了受复杂约束情形下的火箭多级发射上升段制导；文献[11-12]考虑了大气环境对飞行器制导的影响，在此基础上利用最优控制原理对制导方程进行推导；文献[13-14]从控制角的形式等不同角度对迭代制导进行了改进，但均未摆脱传统迭代制导小角度修正假设的限制；文献[15]直接考虑了轨道要素约束下的制导方法，但方程形式不够直观，特别是对乘子变量的消去处理形式复杂，且数值求解时对终端约束方程的权重调整不变。此外，文献[9]虽然直接以推力方向的3分量为控制变量进行了推导，但同样认为位置约束引起的修正为小量。

考虑到上述文献的不足，本文提出了一种基于多终端约束的最优制导方法。结合制导特点对发动机关机点进行优化，并引入权重因子，通过直接迭代求解横截条件方程来提高制导精度，并运用数值仿真验证了该方法的有效性。

1　最优制导方法研究

1.1问题描述

设航天器在某一轨道完成飞行任务后，进入一条自由滑行的转移轨道L1，此后需要选择合适的开关机点进行主发动机的开关机制导，从而进入到新的目标轨道L2，且制导结束后航天器需要以指定的精度在L2轨道上自由滑行至预定的下一次任务点Dfinal。航天器主发动机推力大小不可调。

上述问题涉及到两个方面的需求，一是需要选取合适的开关机点，二是在开关机点确定后，设计合适的制导算法。

1.2开关机点优化

航天器利用主发动机变轨本质上是对脉冲变轨的近似，设脉冲变轨的时刻为tc，由于主发动机的推力和比冲恒定，因此通常的做法是在L1和L2轨道的“交点”处，利用齐奥尔科夫斯基公式计算点火时间Δt，则主发动机的开机时刻为tc-Δt/2，关机时刻为tc+Δt/2。

上述方法所选取的开关机点只是一个初选方案，为保证最终航天器到达Dfinal的精度，该精度直接取决于航天器制导的精度，因此还需要对开关机点进行优化。

通常制导的坐标系有惯性坐标系(包括地心惯性系和发射惯性系)和入轨点轨道坐标系两类，考虑到入轨点轨道坐标系在几何方面更能直观地分析航天器的运动，也更能直观地反映航天器在制导结束后终端约束的满足情况，而航天器制导的精度正是通过终端约束来体现的，因此本文主要对入轨点轨道坐标系下制导的情形进行分析。

在入轨点轨道坐标系(ocf坐标系)下，终端约束通常选为Yocf和Zocf方向的位置约束，以及Xocf、Yocf和Zocf三个方向的速度约束，则目标点和航天器制导结束后到达的实际点如图1所示。

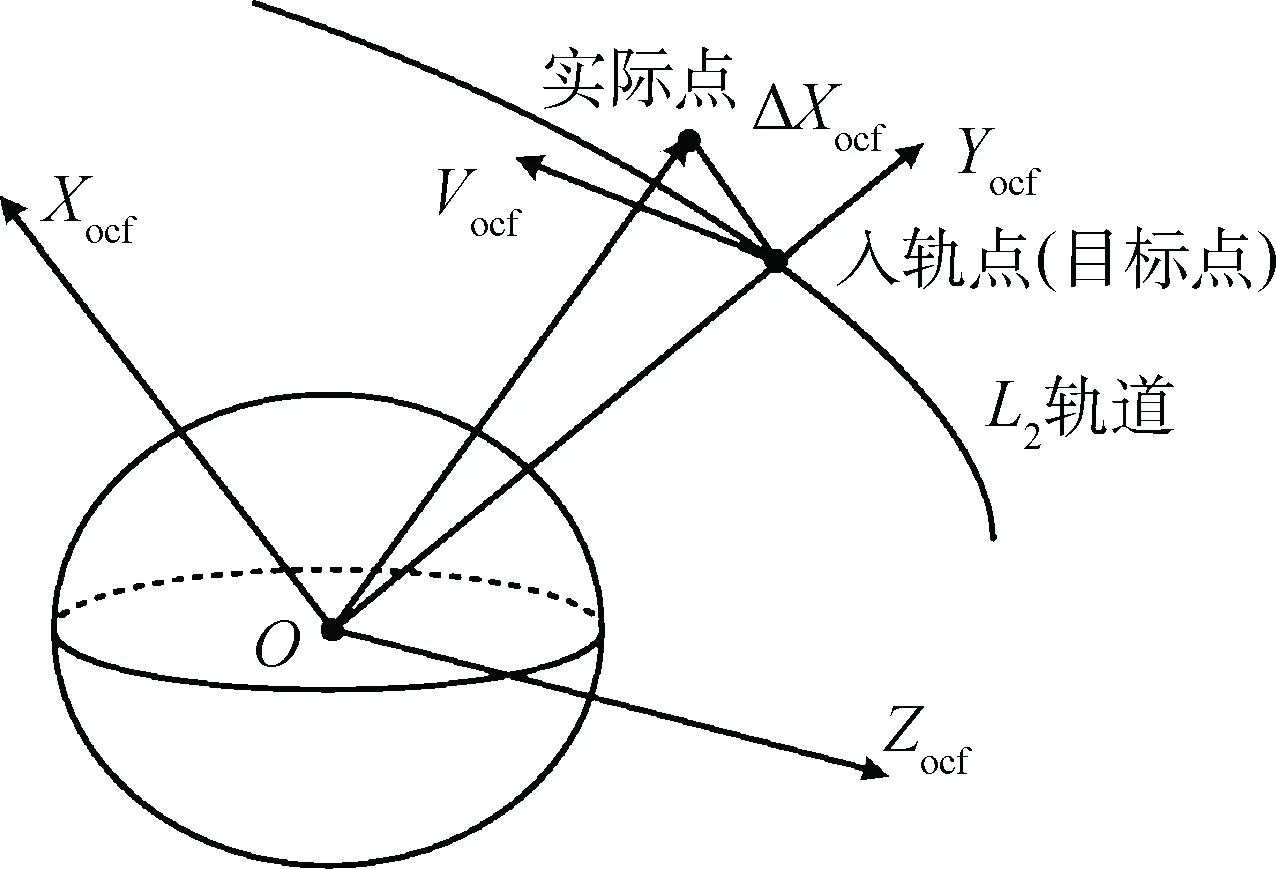
图1　入轨点轨道坐标系下的目标点和实际点Fig.1　Object point and real position in the orbital coordinate system of orbit-insertion point

由图1可知，由于未对Xocf方向的位置进行约束，制导结束后Xocf方向存在位置偏差ΔXocf，如果将目标点向“靠近”实际点的方向“滑行”一些(即目标关机时间比初始计算值多数一些)，那么最终的ΔXocf将会减小一些。具体来说，若ΔXocf为正，则目标点正向“滑行”一些；若ΔXocf为负，则目标点反向“滑行”一些。

与开机点(起始点)相比，关机点(目标点)和误差之间的关系要更为明显。为便于分析，对初选的开机点一般不作调整(即认为初选的开机点足够准确)，而将目标点正向或者反向“滑行”一些，即将L2轨道从“交点”处开始相应的“滑行”时间在Δt/2的基础上，适当增加或者减小一些，因此，这实际上相当于引入了一个新的控制变量，即“滑行”时间的调整量。

由于一旦对目标点进行调整，则整个入轨点轨道坐标系也会发生变化，而制导指令和最后的误差都是在入轨点轨道坐标系中计算的，相应的制导流程也会发生变化，因此调整前后的ΔXocf之间存在一个复杂的关系，无法通过简单的数学推导来得到具体的调整量，需要进行简化分析。

考虑到在入轨点轨道坐标系中，目标点的速度矢量位于OXocfYocf平面内，一个自然的想法是“滑行”时间的调整量与位置偏差ΔXocf和Xocf方向的速度分量Vxocff存在关系。由于ΔXocf相对于L2轨道的高度来说是小量(迭代制导通常假设其余终端约束满足的前提下，Xocf方向的位置约束会尽量满足)，在目标点“靠近”实际点的过程中速度矢量变化很小，且由前面的分析可知，“滑行”时间的调整量应该与ΔXocf正相关，因此不妨将ΔXocf/Vxocff作为“滑行”时间调整的一个基准偏差，根据该偏差来反馈调节“滑行”时间。设“滑行”时间为tcoast，tcoast的调整量正比于ΔXocf/Vxocff，并且可以在前面加一个反馈系数k>0，即“滑行”时间的调整量Δtcoast=kΔXocf/Vxocff，当把ΔXocf/Vxocff看作是误差时，该表达式类似于经典控制理论中的比例反馈修正，根据前面的分析，开机点(起始点)不变，“滑行”时间的调整如图2所示。

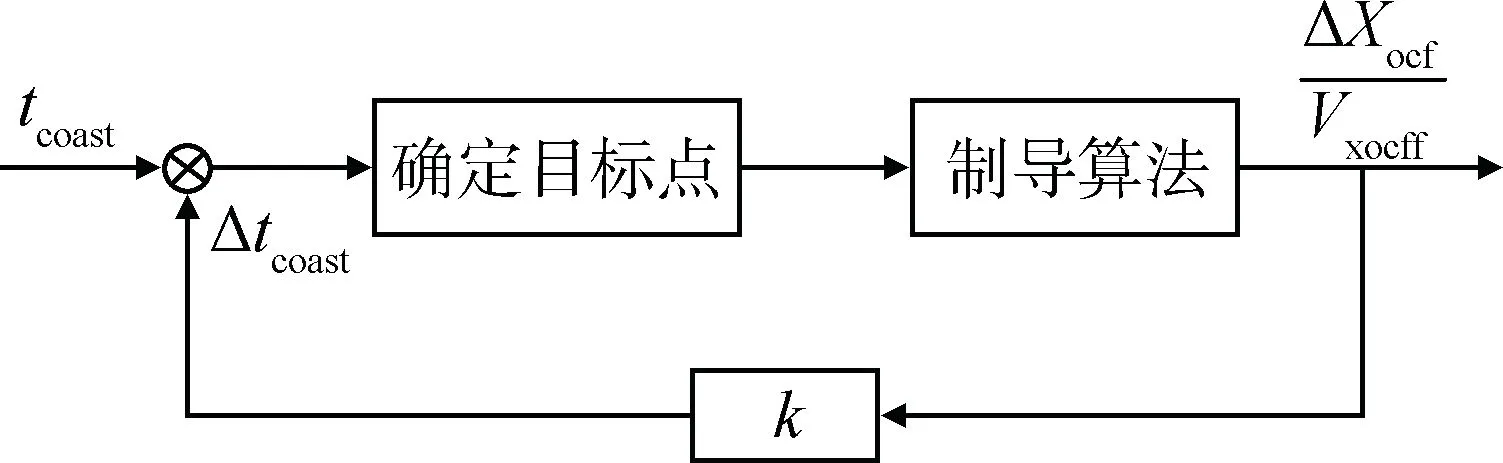
图2　“滑行”时间调整示意Fig.2　Sketch map of coasting time adjustment

由图2，具体的“滑行”时间调整步骤如下：

1)利用齐奥尔科夫斯基公式获得初选的起始点和目标点，即L2轨道从“交点”处正向的初始“滑行”时间tcoast=Δt/2；

2)利用制导算法对设定的起始点和目标点进行制导计算，获得最后的位置偏差ΔXocf和目标点x方向的速度分量Vxocff；

3)计算“滑行”时间的调整量Δtcoast=kΔXocf/Vxocff；

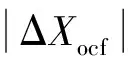
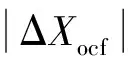
此外，由上述计算步骤可知，在每一次迭代计算过程中，都需要进行一次制导算法的运算来获得最后的位置偏差，制导算法应选择在入轨点轨道坐标系下进行解算。

1.3最优制导算法

传统的迭代制导从最优控制原理出发，但并没有对获得的方程组直接求解，而是作了一定的简化假设，特别是假设了指令角的形式，在此基础上推导出指令角的相关参数。本文在迭代制导的基础上，介绍一种直接基于最优控制原理的制导方案，通过直接考虑终端约束来获得相关方程，对相关方程进行求解来获得姿态指令角，整个制导过程的思想更为清晰和明确，且同样满足最终的入轨精度需求。

经过上述处理后，可得到无量纲化的航天器运动方程为

(1)

式中：r为航天器位置矢量；v为航天器速度矢量；g为地球引力加速度矢量；T为航天器的推力大小；ms为恒定的秒流量；m0为初始质量；u为推力方向矢量。

下面建立航天器制导的最优控制模型，系统方程即为式(1)的状态空间形式，取状态变量为

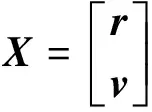
(2)

控制量即推力方向u，即

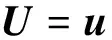
(3)

则状态方程为

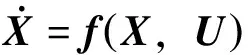
(4)

性能指标为燃料最省，亦即推力飞行时间最短，即

(5)

约束条件为推力方向的单位化约束，即

(6)

对于边界条件，初始时刻的状态给定，即

(7)

E1=Xf(2)-Yocff=0，E2=Xf(3)-Zocff=0，

(8)

列写哈密顿函数：

(9)

式中：λr、λv和λu为协态变量，则相应的伴随方程为

(10)

由式(10)可解得

(11)

式中：λr0和λv0分别为λr和λv的初值。

控制方程为

(12)

考虑约束式(6)，可解得

(13)

于是由系统方程解得最优终端状态为

(14)

式(14)中的积分运算可利用数值插值积分公式进行。

终端约束对应的横截条件为

(15)

(16)

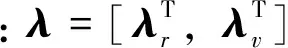
(17)

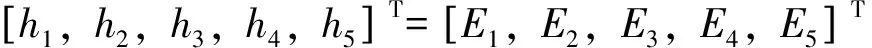
由于：

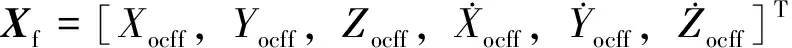
(18)

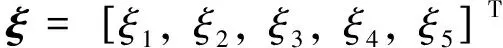
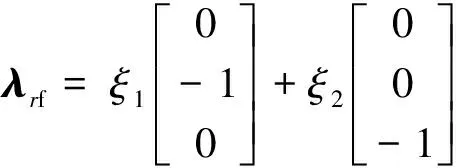
(19)

(20)

(21)

式(8)、式(17)和式(21)组成了所有7个横截条件方程，结合协变量和最优状态量的表达式(10)和式(14)，则横截条件方程组含λ0和tf7个变量，由于最优终端状态可表示为λ0和tf的函数，而最优终端状态需要满足式(8)中的终端约束，因此可通过数值迭代求解出λ0和tf。在解得λ0和tf后，当前时刻的控制量即为

(22)

需要说明的是，上述方法通过直接迭代求解横截条件方程组来获得协态变量初值，而没有像传统迭代制导方法那样对指令角度做简化假设，因此理论上来说可以获得最优解。在具体应用时，数值求解的精度决定了获得控制解的好坏，这一点主要体现在终端约束满足的效果上。下面对此进一步进行分析。

2　终端约束的权重调整

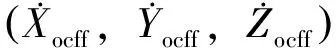
(23)

(24)

(25)

(26)

(27)

由于入轨点轨道坐标系本身的特点，Yocff是一相当大的数，而理论上Zocff=0，因此直接以式(23)～(27)作为终端约束进行控制量的求解时，由于E1与其余4个约束的量级相差较大，直接迭代求解时会使得终端约束E1实际的值较大，因此需要对原始的终端约束条件进行转化。

考虑到通常情况下在地心惯性坐标系下目标点3个方向的位置分量大致处于同一量级，因此，如果能够将入轨点轨道坐标系下的位置约束等效转化为地心惯性坐标系下的位置约束，那么理论上来说对于迭代求解协态变量的初值没有任何影响，但从数值角度来说将更为容易处理。

(28)

则地心惯性坐标系和入轨点轨道坐标系下的位置约束关系满足

(29)

当入轨点轨道坐标系下的Y和Z方向的位置约束满足，即E1=E2=0时，ΔXchi、ΔYchi和ΔZchi之间存在固定的比例关系，即无论(Xf(1)·Re-Xocff)取何值，均应有

(30)

此时地心惯性坐标系下等效的两个终端约束为

(31)

(32)

在具体利用式(29)计算ΔXchi、ΔYchi和ΔZchi时，可直接将[Xf(1)·Re-Xocff]替换为某一常数C，同时，为进一步提高数值求解精度，对约束E1和E2可以进行相应的权重调整，即分配相应的权重系数k1和k2，从而有

(33)

类似地，对入轨点轨道坐标系下的3个速度约束E3、E4、E5也可以进行相应的权重调整，相应的权重因子取为k3、k4、k5。

总结来说，转换后的5个等效终端约束为

(34)

在获得等效的终端约束后，每一次制导循环中，通过对式(34)和式(17)、式(21)直接迭代求解来获得协态变量初值，进一步由式(22)求解相应的控制角。

3　仿真验证

3.1标准条件仿真

在发射惯性系下，航天器初始的位置为[1 865 014.8，40 816.2，150 433.5]Tm，速度为[7 412.601，-2 160.522，-130.991]Tm/s。Dfinal点的位置为[-5 967 060.6，-9 089 564.4，-89 871.6]Tm，速度为[-3 054.343，7 167.845，286.663]Tm/s。

仿真计算步长选为10ms，终止迭代计算条件选为剩余分析时间小于5s时，3次关机点条件为剩余飞行时间小于0.1s时。终端约束的权重因子取为k1=10-4、k2=10-4、k3=10-3、k4=10-3、k5=10-4。关机点的反馈系数k取为8。

首先对初选的开关机点直接进行制导仿真，制导结束后的偏差数据如表1所示。

表1　位置偏差和速度偏差(初始开关机点)

由表1中的数据可知，由于没有对X方向的位置进行约束，因此最终X方向的位置偏差比较大，利用本文中的方法对关机点进行调整，迭代修正计算的次数为2次，第一次修正后X方向的位置偏差为25.806 7m，第二次修正后X方向的位置偏差为5.738 9m，可见反馈系数的选取能够使得X方向的位置偏差朝减小的方向进行。

对修正后的开关机点进行制导仿真，实际飞行时间为166.890 0s，在入轨点轨道坐标系下的制导结果如图3～6所示。

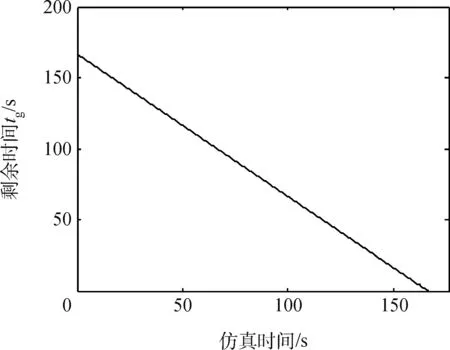
图3　剩余时间示意Fig.3　Residual time sketch map

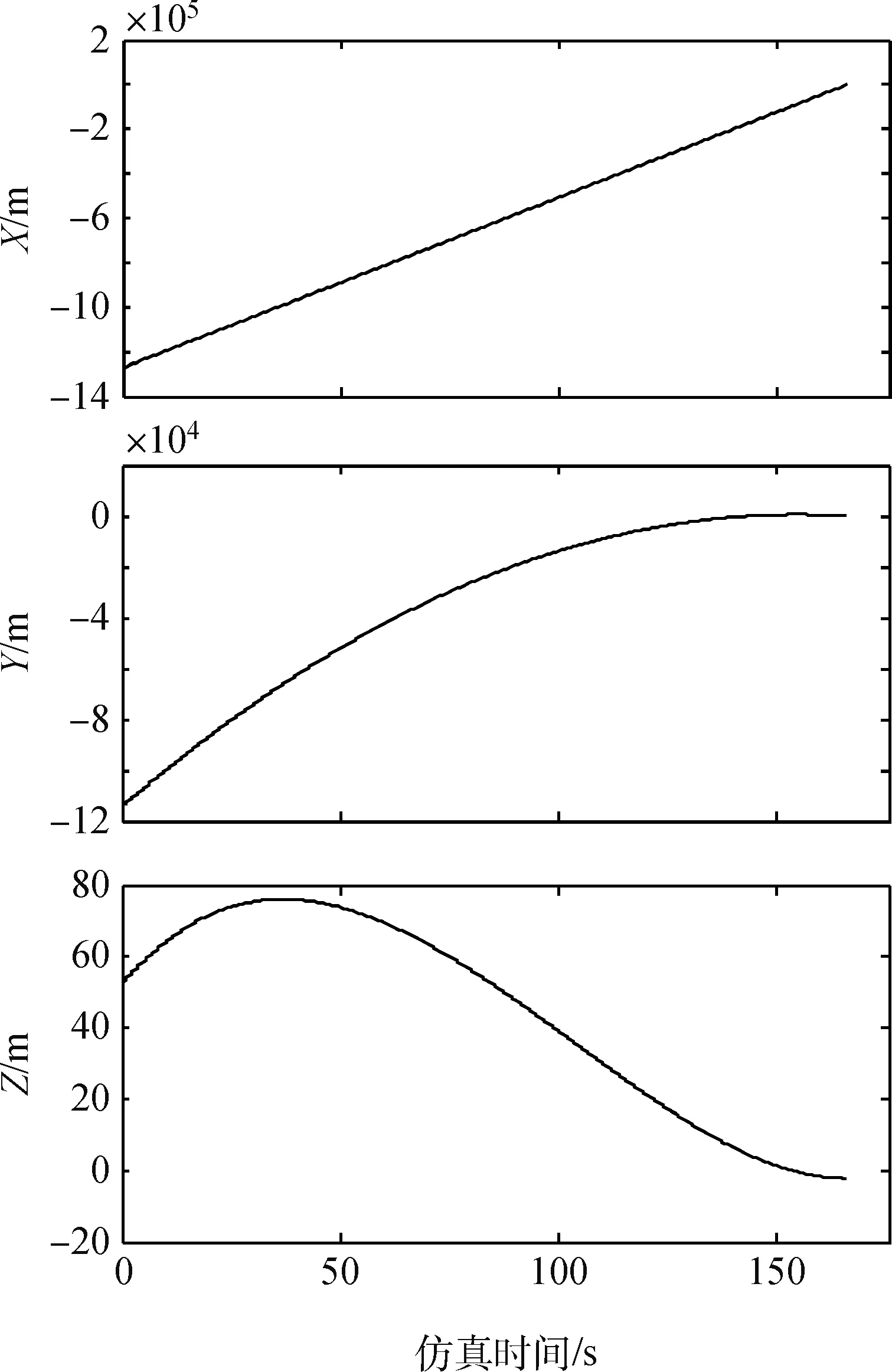
图4　位置偏差Fig.4　Position deviation in the XYZ-direction

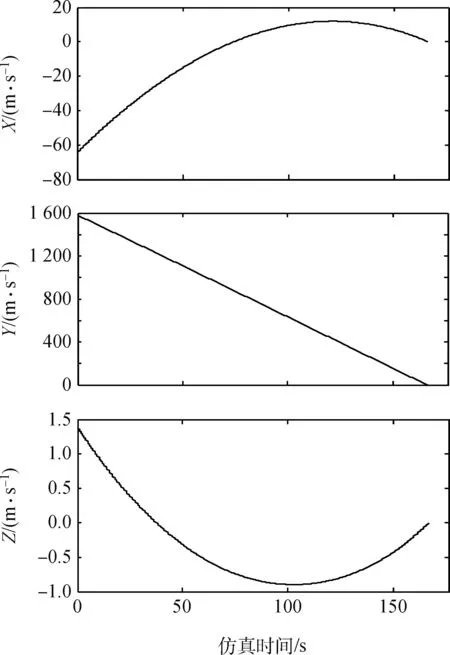
图5　速度偏差Fig.5　Velocity deviation in the XYZ-direction

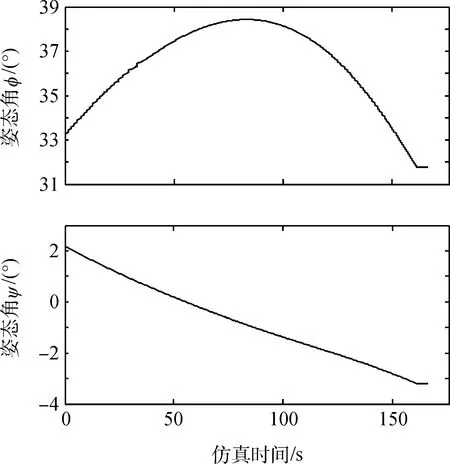
图6　姿态角变化Fig.6　Attitude angleφandψ

由图3～6的仿真结果可以看出，在整个制导过程中，剩余时间逐渐减小到0，3个方向的位置和速度误差最终也趋于0，制导结束后的偏差数据如表2所示。

表2　位置偏差和速度偏差(修正开关机点)

从表1和表2可以看出，X方向的终端位置约束精度提高了159.535 5m,此后航天器开始自由滑行，滑行仿真在地心惯性坐标系下解算，滑行时间为745.1s，将最终到达Dfinal点时的仿真计算结果与所要求的相比结果如表3所示。

表3　到达Dfinal点时的偏差

由表3中的数据可知，航天器到达最终点时的各项偏差均在容许范围内，最终的经度和纬度偏差均小于0.5°，高度偏差小于200m，速度倾角偏差小于0.005°，速度方向角偏差小于0.3°、速度大小偏差小于1.5m/s，从而表明了本文所提方法的有效性。

3.2蒙特卡罗打靶仿真

下面对航天器初始的位置和速度存在偏差的情况进行蒙特卡罗打靶仿真。假定位置和速度偏差相互独立且服从正态分布，均值取为第3.1节中的数据，具体取值如下：

在发射惯性系下，航天器初始的位置为[1 865 014.8，40 816.2，150 433.5]Tm，速度为[7 412.601，-2 160.522，-130.991]Tm/s。

X方向位置偏差：均值μpx=1 865 014.8m，标准差σpx=1km。

Y方向位置偏差：均值μpy=40 816.2m，标准差σpy=100m。

Z方向位置偏差：均值μpz=150 433.5m，标准差σpz=300m。

X方向速度偏差：均值μvx=7 412.601m/s，标准差σvx=1m/s。

Y方向速度偏差：均值μvy=-2 160.522m/s，标准差σvy=0.5m/s。

Z方向速度偏差：均值μvz=-130.991m/s，标准差σvz=0.3m/s。

针对上述偏差数据，其余仿真设置与第3.1节相同，进行蒙特卡洛仿真，样本点取为2000，某一次的仿真统计结果如图7～9所示。

图7　开关机点优化迭代次数Fig.7　Iteration times of switch on and off instants optimization

图8　初始关机点X位置偏差大小Fig.8　Absolute position deviation of initial switch off instants in the X-direction

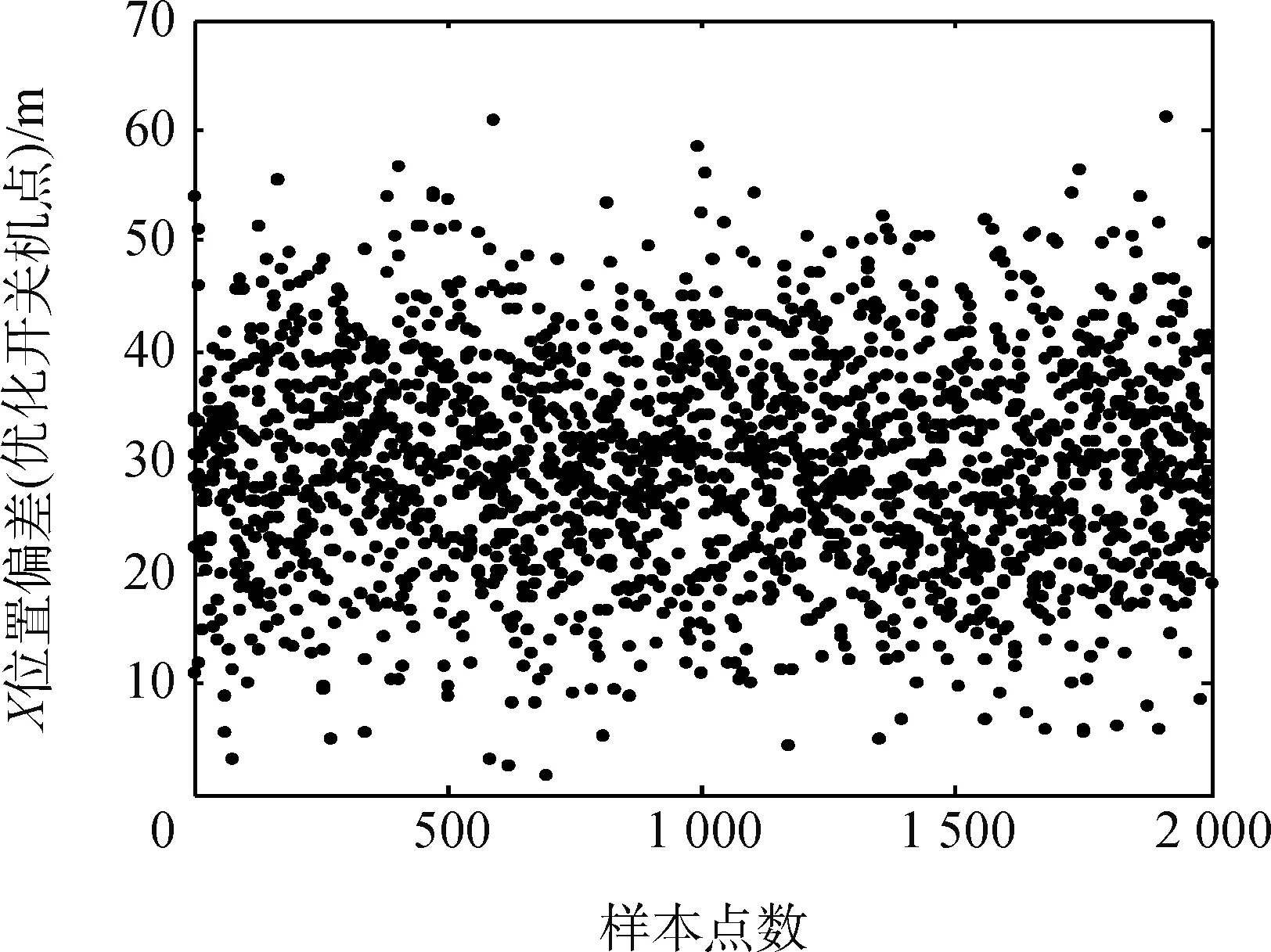
图9　优化关机点X位置偏差大小Fig.9　Absolute position deviation of optimized switch off instants in the X-direction

进一步的统计结果如表4所示。

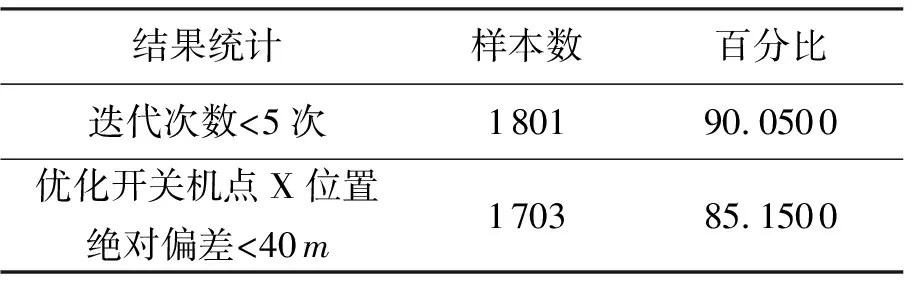
表4　制导结束时的偏差蒙特卡罗仿真统计结果

由图7～9和表4中的统计结果可知，大部分的样本点，经过关机点优化后能够保证X方向位置偏差大小在40m以内，且迭代求解次数不超过5次。

最终到达Dfinal点时的仿真统计结果表5所示。

由表5中的统计结果可知，航天器到达最终点时的仿真，大约70%的样本点能达到容许的偏差范围，从而表明了所提方法对航天器初始位置和速度偏差具有一定的适应性。

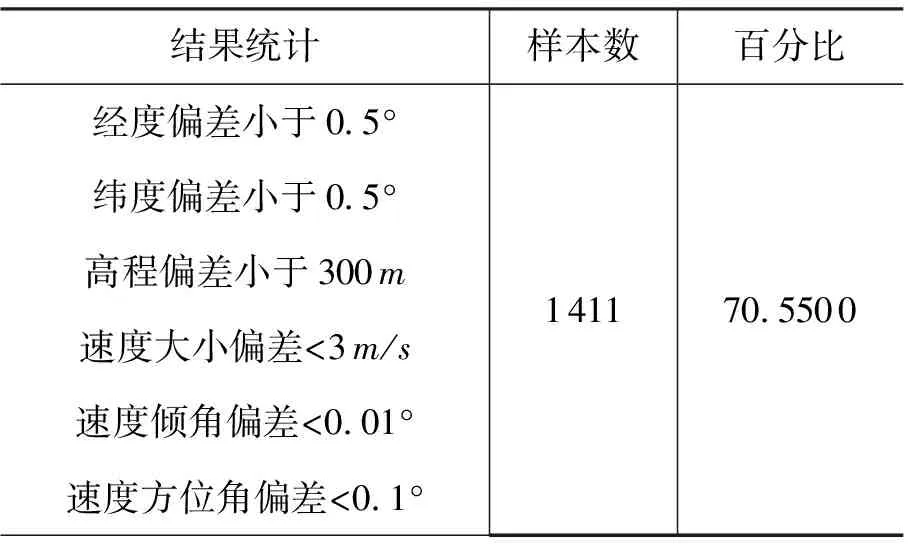
表5　到达Dfinal点导的偏差蒙特卡罗仿真统计结果

4　结束语

本文针对传统迭代制导方法的不足，首先对关机点进行优化，以减小未被满足的终端位置约束的影响，进一步，直接从最优控制原理出发，推导控制角需要满足的方程并进行求解，摆脱了传统迭代制导小角度修正的假设，同时对终端约束进行等效转换和权重分配，从而提高了数值求解的精度和制导方法的适应性，航天器最终能以指定精度到达下一次任务点，仿真结果表明了所提方法的有效性。

References)

[1]王召辉，金磊，贾英宏，等. 上面级轨道转移段姿态控制技术[J]. 中国空间科学技术，2014，10(5): 41-48,55.

WANG Z H，JIN L，JIA Y H，et al. Attitude control technology of upper stage during orbital transfer[J]. Chinese Space Science and Technology，2014，10(5): 41-48,55(in Chinese).

[2]周洋，闫野，黄煦，等. 航天器轨道机动的闭环控制精度分析[J]. 宇航学报，2014，35(9): 1015-1021.

ZHOU Y，YAN Y，HUANG X，et al. Accuracy analysis of closed-Loop control for spacecraft orbit naneuver[J]. Journal of Astronautics，2014，35(9): 1015-1021(in Chinese).

[3]王常虹，曲耀斌，陆智俊，等. 航天器有限推力轨道转移的轨迹优化方法[J]. 西南交通大学学报，2013，48(2): 390-394.

WANG C H，QU Y B，LU Z J，et al. Trajectory optimization method for spacecraft orbit transfer with finite thrust[J]. Journal of Southwest Jiaotong University，2013，48(2): 390-394(in Chinese).

[4]廖飞，季海波，解永春. 追踪器本体坐标系下航天器姿轨一体化控制律设计[J]. 控制与决策，2015，30(9): 1679-1684.

LIAO F，JI H B，XIE Y C. Integrated orbit and attitude control for spacecraft in body fixed coordinate of chaser[J]. Control and Decision，2015，30(9):1679-1684(in Chinese).

[5]LU P，FORBES S，BALDWIN M. A Versatile powered guidance algorithm[C]∥2012 AIAA Guidance，Navigation，and Control Conference. Minnesota: Minneapolis，2012.

[6]HAEUSSERMANN W. Saturn launch vehicle′s navigation guidance，and control system[J]. Automatica，1971，7(5): 537-556.

[7]韩祝斋. 用于大型运载火箭的迭代制导方法[J]. 宇航学报，1983，4(1): 10-16.

HAN Z Z. An iterative guidance method for the large launch vehicle[J]. Journal of Astronautics，1983，4(1): 10-16(in Chinese).

[8]陈新民，余梦伦. 迭代制导在运载火箭上的应用研究[J]. 宇航学报，2003，24(5): 484-489.

CHEN X M，YU M L. Study of iterative guidance application to launch vehicles[J]. Journal of Astronautics，2003，24(5)： 484-489(in Chinese).

[9]茹家欣. 液体运载火箭的一种迭代制导方法[J]. 中国科学: E 辑，2009, 39(4): 696-706.

RU J X. An iterative guidance method of liquid launch vehicle[J]. Science in China Series E-Technological Sciences，2009 ,39(4): 696-706(in Chinese).

[10]LU P，GRIFFIN B J，DUKEMAN G A，et al. Rapid optimal multiburn ascent planning and guidance[J]. Journal of Guidance，Control，and Dynamics，2008，31(6): 1656-1664.

[11]LU P，SUN H，TSAI B. Closed-loop endoatmospheric ascent guidance[J]. Journal of Guidance，Control，and Dynamics，2003，26(2): 283-294.

[12]LU P，PAN B. Highly constrained optimal launch ascent guidance[J]. Journal of guidance，Control，and Dynamics，2010，33(2): 404-414.

[13]吴楠，程文科，王华. 运载火箭迭代制导方法的改进研究[J]. 动力学与控制学报，2009，7(3): 279-282.

WU N，CHENG W K，WANG H. An improved iterative guidance method for launch vehicle[J]. Journal of Dynamics and Control，2009，7(3): 279-282(in Chinese).

[14]王炀，唐硕. 最优真空飞行轨迹设计和制导方法研究[J]. 计算机仿真，2011，28(10): 78-82.

WANG Y，TANG S. Optimal vacuum flight trajectory design and guidance method[J]. Computer Simulation，2011，28(10):78-82(in Chinese).

[15]傅瑜，陈功，卢宝刚，等. 基于最优解析解的运载火箭大气层外自适应迭代制导方法[J]. 航空学报，2011，32(9): 1696-1704.

FU Y，CHEN G，LU B G，et al. A vacuum adaptive iterative guidance method of launch vehicle based on optimal analytical solution[J]. Acta Aeronautica et Astronautica Sinica，2011，32(9): 1696-1704(in Chinese).

(编辑：车晓玲)

An optimal guidance method based on multiple terminal constraints

LI Chaobing*，WANG Jinlin，LI Hai

Beijing Aerospace Automatic Control Institute，Beijing 100854，China

Since the thrust amplitude of the main engine on spacecraft is unadjustable，a multiple terminal constrain based optimal guidance method was proposed，considering the deficiency of small correction angle assumption of conventional iterative guidance under five terminal constrains. An optimal control model was established in the orbit injection orbital coordinate frame. Transversality equations ware directly solved by iteration to obtain the guidance angle command.The switch on and off instants were then optimized to reduce the influence of unsatisfied terminal constraints. Besides，the five equivalent terminal constraints in the geocentric inertial coordinate frame were derived and appropriate weight factors were adjusted to improve the precision of numerical solving of guidance equations. Simulations on standard conditions demonstrate that the proposed guidance method has increased the precision of unsatisfied terminal constraints by 159.535 5 m，compared with the conventional iterative guidance. The Monte Carlo simulations show the adaptability of the proposed method to the initial bias of the spacecraft position and velocity.

spacecraft orbit transfer；iterative guidance；optimal control；coordinate transformation；switch on and off instants optimization；weight adjustment

10.16708/j.cnki.1000-758X.2016.0052

2016-05-03；

2016-07-07；录用日期：2016-08-22；

时间：2016-09-2113:41:23

http:∥www.cnki.net/kcms/detail/11.1859.V.20160921.1341.005.html

李超兵(1981-)，男，硕士，高级工程师，lcbpku@163.com，研究方向导航制导与控制

TP249，V448.22

A

http:∥zgkj.cast.cn

引用格式：李超兵，王晋麟，李海. 一种基于多终端约束的最优制导方法[J].中国空间科学技术，2016，36(5)：9-17.

LICB，WANGJL，LIH.Anoptimalguidancemethodbasedonmultipleterminalconstraints[J].ChineseSpaceScienceandTechnology，2016，36(5)：9-17(inChinese).