卫星群反作用飞轮的故障诊断方法研究
2016-11-09王嘉轶闻新张婉怡
王嘉轶,闻新,张婉怡
南京航空航天大学 航天学院,南京 210016
卫星群反作用飞轮的故障诊断方法研究
王嘉轶,闻新*,张婉怡
南京航空航天大学 航天学院,南京 210016
卫星群飞行技术是航天领域的新兴技术,多个低成本小卫星可以完成较为艰巨的太空任务,但与此同时也会带来更多的故障问题。面对复杂的空间环境,针对卫星群可能发生的故障问题,提出了一种分布式卫星群系统故障诊断方案,通过基于Elman神经网络的故障诊断方法完成对卫星群姿态控制系统的故障诊断。试验结果表明,该方案能够快速检测出卫星群中反作用飞轮发生的故障,并且让邻近卫星通过神经网络也能检测到该故障的发生,表现出很好的准确性和实时性,在实际应用中有效可行。
卫星群;神经网络;故障诊断;姿态控制;反作用飞轮
卫星群飞行技术是空间技术的新兴领域,也是国内外航天领域的发展方向。传统的太空飞行任务是利用昂贵的大卫星进行的。然而,与单颗大卫星相比,小卫星群在运行成本、鲁棒性、灵活性和容错能力方面都有明显的优势,并且可以完成更为艰巨的太空任务,所以越来越受到广泛关注。近年来,国内外很多学者都致力于卫星群系统飞行技术的研究[1-3]。Scharf等人[4-5]提出了5种不同的编队飞行控制方案。另外,基于单积分一致性理论和基于双积分方法的多智能体(mlti-agent)系统也在文献[6-8]中进行了有效性论证。
然而,这些卫星群的飞行方案都是建立在理想操作环境下的,一旦出现故障,会给卫星群飞行任务带来严重的影响。传统意义上,卫星的地面监控系统已经能够完成航天器的故障诊断。但是,当卫星发生异常时,由于需要下载大量的遥测数据进行分析,人工故障检测和恢复在实时性和有效性方面都会受到一定的影响。另一方面,由于卫星群系统的卫星数量较多,地面故障诊断系统需要耗费更多资源,这样也会增加卫星飞行任务的成本。因此,卫星群系统需要具备自主故障检测、隔离和故障恢复的能力。文献[9]就这些问题提出了基于分层式自主故障检测与隔离机制的航天器编队飞行系统。为了能够检测出系统发生的故障,设计了分别为子系统部件级、子系统级、系统级和群系统级的4层式编队飞行系统故障诊断算法,并利用模糊规则来对不同层级间的故障关系进行故障检测和说明。基于上述研究结果,文献[10]利用模糊推理算法完成了主从式编队飞行任务中姿态控制子系统的部件级故障诊断。另外,分布式故障诊断方式也得到了广泛的应用。文献[11]利用了几何方法来设计基于分布式故障检测滤波器的航天器编队。每个航天器不仅能够检测和隔离自身发生的故障,而且同样可以诊断其他航天器故障。对于故障诊断算法方面,文献[12-13]也同样运用几何方法实现了基于观测器设计的故障诊断。除此之外,基于模型的故障诊断方法,如卡尔曼滤波法和基于观测器方法也都被运用到卫星群的自主故障诊断上[14-17]。然而,要想建立精准的系统模型是非常困难的,这限制了基于模型的故障诊断方法的发展。所以,机器学习算法,如聚类分析算法和神经网络算法,在近年得到了更多的关注。文献[18-19]就是利用动态神经网络模拟了卫星推进器的动力学特性,然后运用该模型进行卫星编队系统的故障诊断。在拥有充分数据训练的情况下,就可以建立系统的动态神经网络系统。但是,当数据在实际过程中很难获得的情况下,该方法将不再适用。
针对上述研究成果和群系统在故障诊断中存在的问题,本文提出了基于Elman神经网络的卫星群故障诊断方案。首先,通过对Elman神经网络的建立,研究单颗卫星姿态控制系统的故障诊断问题。然后以三星为例,对基于虚拟结构的卫星群中的执行器故障问题进行仿真分析,验证所提出的卫星群故障诊断方案的有效性和可行性。
1 卫星姿态系统描述
卫星姿态控制方法主要分为两类,主动控制方法和被动控制方法。其中主动控制方法包括三轴姿态稳定、动量偏移等,被动控制方法有重力梯度稳定、气动力矩稳定以及自旋稳定等。其中,三轴姿态稳定的主动姿态控制方法精度最高,是卫星姿态中最常用的方法,所以本文采用这种方法来进行卫星姿态的稳定性控制。
1.1卫星姿态系统模型
卫星的姿态运动是指其绕自身质心的运动,所以姿态控制问题可以抽象为刚体姿态的控制问题。在卫星的本体坐标系中,Ox,Oy,Oz轴为卫星的主惯量轴。利用刚体的动量矩定理,得到卫星姿态动力学方程:
(1)
式中:ω1、ω2、ω3为卫星空间转动角速度沿坐标轴Ox、Oy、Oz方向上的分量(即卫星的滚转角速度、偏航角速度和俯仰角速度);I1、I2、I3分别为卫星绕坐标轴Ox、Oy、Oz的转动惯量;M1、M2、M3分别为作用在卫星上相对于质心O的控制扭矩在坐标轴Ox、Oy、Oz方向上的分量。
定义θ1、θ2、θ3为卫星本体坐标系相对于质心平动坐标系的3个欧拉角,分别为滚转角、偏航角和俯仰角,并按照3-1-3方式旋转(即按照俯仰-滚转-俯仰)。最终得到卫星空间转动角速度在本体坐标系中的分量ω1、ω2、ω3,即将卫星姿态从本体坐标系变换到质心平动坐标系,这就是卫星的姿态运动学方程:
(2)
联立式(1)和式(2),整理后得到卫星姿态系统的状态方程:
(3)
由式(3)可知,卫星姿态运动学方程是一个
强非线性模型,共有6个状态变量。
1.2反作用飞轮
在姿态控制系统中,执行机构主要是通过产生力或力矩来控制卫星的姿态变化。其中,反作用飞轮由于其高精度而被普遍应用于卫星姿态主动控制系统中。在一般情况下,反作用飞轮是由直流无刷电机驱动的飞轮构成。一个高精度的反作用飞轮的内部结构模型如图1所示[20]。
该模型主要包括5个模块:电机扭矩控制模块、转速限制模块、电动势扭矩限制模块、电机扰动模块及轴承的摩擦扰动模块。反作用飞轮中母线电流Ibus和黏性扭矩τv表示如下:
(4)
(5)
式中:Vbus为母线电压;Im为电机电流;ω为反作用飞轮角速度;T为工作温度。反作用飞轮中其他参数值、对应单位及其物理意义如表1[20]所示。

图1 反作用飞轮模型结构Fig.1 Block diagram of reaction wheel
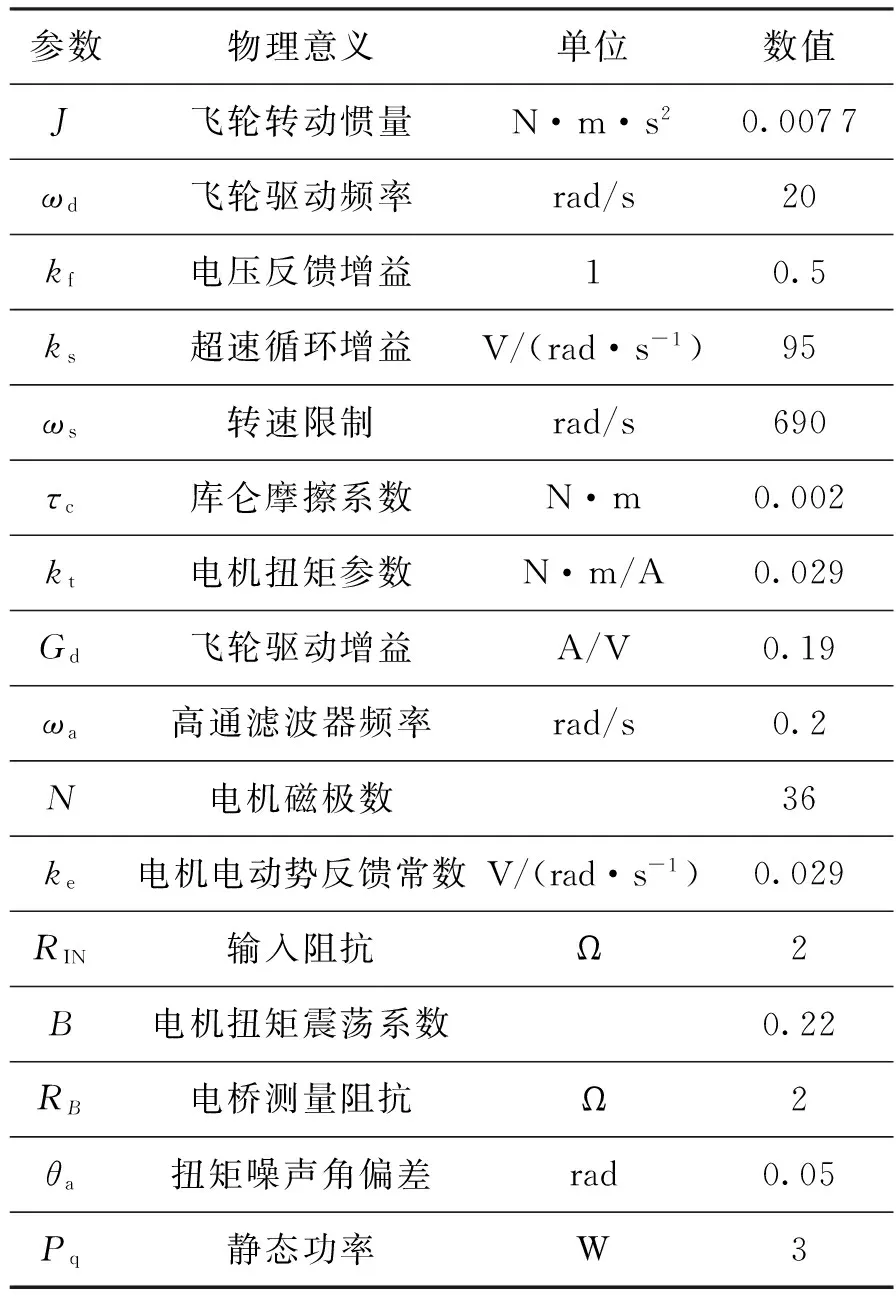
参数物理意义单位数值J飞轮转动惯量N·m·s20.0077ωd飞轮驱动频率rad/s20kf电压反馈增益10.5ks超速循环增益V/(rad·s-1)95ωs转速限制rad/s690τc库仑摩擦系数N·m0.002kt电机扭矩参数N·m/A0.029Gd飞轮驱动增益A/V0.19ωa高通滤波器频率rad/s0.2N电机磁极数36ke电机电动势反馈常数V/(rad·s-1)0.029RIN输入阻抗Ω2B电机扭矩震荡系数0.22RB电桥测量阻抗Ω2θa扭矩噪声角偏差rad0.05Pq静态功率W3
2 卫星姿态控制系统故障诊断
2.1Elman神经网络
Elman神经网络是由J.L.Elman于1990年提出的一种动态反馈网络,首先应用于语音问题的处理上[21]。在系统辨识、预测和控制领域,已有很多学者对Elman神经网络或者改进Elman神经网络进行研究。Elman神经网络一般包含4层,分别是输入层、隐含层、承接层和输出层。该网络相当于一个从隐层输出到隐层输入进行反馈连接的动态神经网络。其中,承接层用来记忆前一时刻的输出值并返回给网络的输入。因此,隐含层具有映射外部输入以及前一时刻期望输出的特点。隐含层的传递函数一般采用非线性函数,取sigmoid函数。为了提高Elman神经网络的非线性处理能力,文献[22]提出了基于Elman网络的优化算法。优化后Elman神经网络的不同之处在于其具有固定增益的自反馈环节,使得网络具有更好的动态记忆功能,图2为优化的Elman神经网络的结构[23]。

图2 优化的Elman神经网络结构Fig.2 Structure of modified Elman neural network
输入层到输出层的动态关系为:
Y(k)=WyX(k)=
(6)
式中:U(k)、Y(k)为网络输入和输出向量;X(k)、Xc(k)为隐含层和承接层的输入向量;Wc、Wu、Wy为承接层、输入层和隐含层的连接权矩阵。Elman网络的数学模型表达方法表示如下:

(7)
式中:Wyc是隐含层到承接层的连接权矩阵。与此同时,经过改进的Elman神经网络的数学模型表示方法如下:
(8)
设Y(k)和Yd(k)为系统的实际输出和期望输出响应,那么Elman网络的目标函数(误差函数)可以表示为:
(9)
由于优化后的Elman神经网络还是通过BP算法来调节网络的连接权值,所以无法避免BP网络带来的如收敛速度慢且易于陷入局部极小值等问题。因此,针对Elman神经网络的这些问题,本文利用遗传算法(GA)对Elman神经网络进行权值的优化。
遗传算法是一种具有广泛适用性的搜索算法[24]。在自然选择和种群遗传进化学的基础上,通过随机迭代和进化使得种群能够适应环境的变化。这是遗传算法的基本原则,称之为“适者生存”。GA将优胜劣汰原则和信息随机交换方法相结合,前者消除了种群中的非适应因素,后者充分利用了种群中的现有信息共享机制,从而可以有效地加快搜索过程。并且基于多点并行搜索的特点,GA就能避免搜索系统陷入局部极值点的问题出现。所以,GA可以通过选择、复制、交叉和变异操作,在大概率解空间中搜索全局中的最优解或次优解。
Elman神经网络的拓扑结构是由输入/输出样本参数的数量决定的,所以首先可以通过GA优化参数值和个体编码的长度来改进网络的拓扑结构。另外,Elman神经网络的权值和阈值都是通过随机初始化得到的,这对网络的训练有很大的影响。然而,这里无法通过计算直接获得网络权值和阈值的初始值。因此遗传算法的引入可以帮助网络寻找到最优的初始权值和阈值。这样,基于遗传算法改进的Elman神经网络可以更好地对输入值进行预测。并且遗传算法具有并行搜索的特性,可以避免Elman神经网络陷入局部最优的问题,保证了神经网络算法的快速和稳定的原则。基于遗传算法改进的Elman神经网络的算法流程如图3所示。

图3 改进的Elman神经网络的算法流程Fig.3 Flow chart of Elman neural network improved by GA
2.2卫星姿态控制系统
本文采用基于Elman网络的动态神经网络来搭建卫星三轴稳定姿态系统的故障诊断方案,神经网络是卫星姿态控制系统故障诊断的判断依据。其中Vcomm和τz/est作为神经网络的输入值和输出值,分别表示实际系统的指令电压值和控制力矩的估计值,τz/act是实际控制系统的控制力矩。通过扭矩传感器测得的卫星反作用飞轮实际输出信号和通过神经网络得到的估计输出信号的差就是我们需要获取的残差信号,该信号可以用于卫星执行机构的健康状态测定。所以,经过训练的神经网络可以通过残差生成来进行卫星姿态控制系统中反作用飞轮的故障诊断,如图4所示。

图4 基于神经网络的卫星姿态故障诊断系统Fig.4 Neural network based fault diagnosis system of satellite

(10)
2.3仿真分析
在试验仿真中,首先对卫星姿态控制系统中执行器机构的反作用飞轮进行建模,然后对卫星每个轴上反作用飞轮的输入输出参数即指令电压Vcomm和控制力矩τz进行数据采集并利用改进的Elman神经网络进行训练。训练过程是从一个相对较小的网络结构开始,通过逐步增加神经元个数和改进网络层数,直到达到误差允许范围内的性能要求。神经网络的学习速率设置为0.05,训练过程是在不同噪声条件下通过蒙特卡洛方法进行步长为0.01 s的3 000步仿真。通过500次的训练迭代后均方差的平均值为0.005 908,满足性能指标的要求。卫星三轴姿态训练后的性能指标如图5所示。

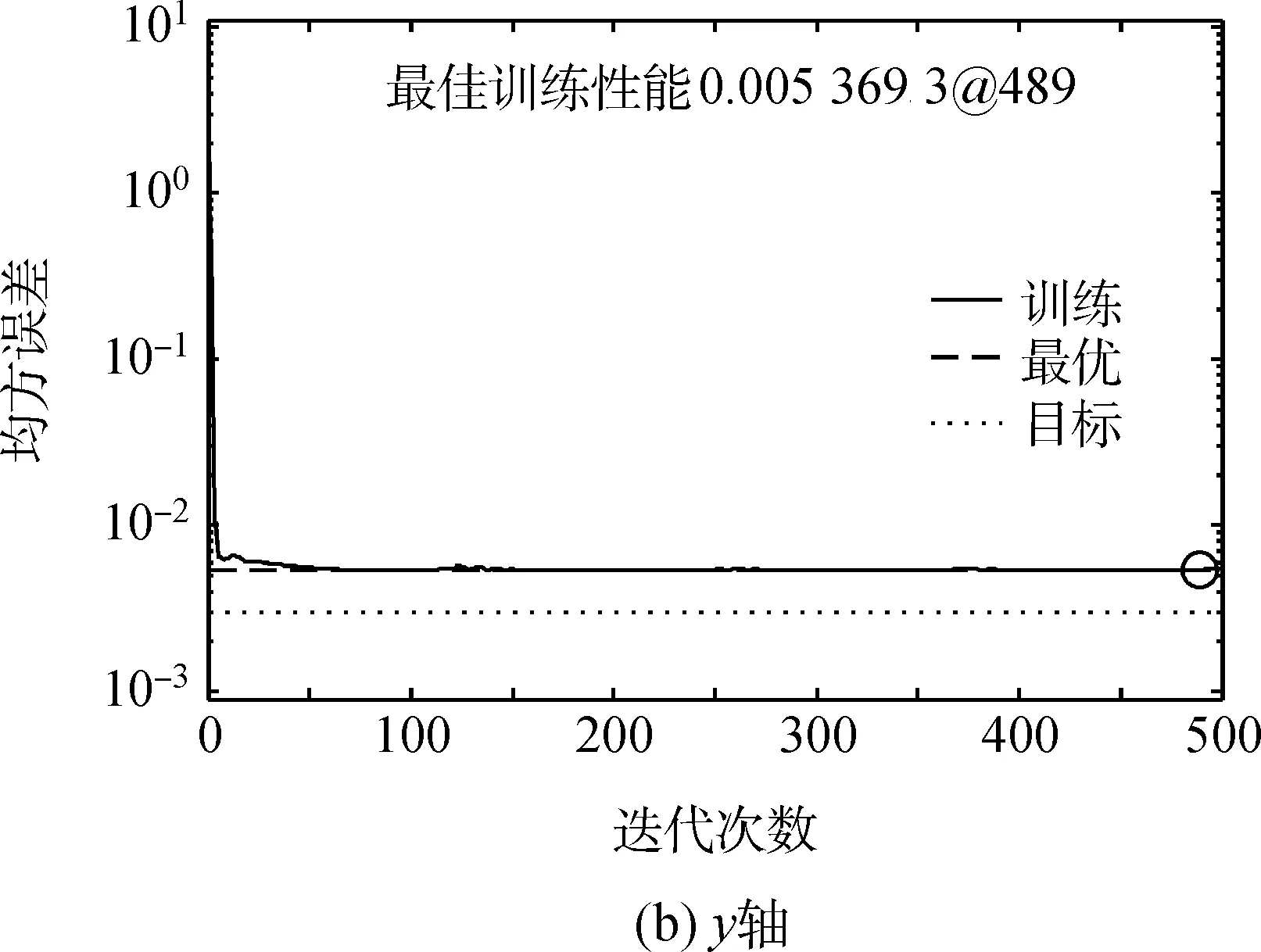

图5 神经网络训练后的性能指标Fig.5 The performance index curve of neural network training
对于卫星姿态控制系统,在一般情况下,反作用飞轮有两种情况容易发生故障,可能导致控制系统严重损坏甚至灾难性故障。下面将通过卫星姿态控制系统的故障问题来验证所提出的故障诊断方案的可实行。
(1)电机电流故障
当电机电流下降的时候,反作用飞轮提供不了足够的控制扭矩,这将导致姿态控制回路的稳定性下降,引起一系列姿态故障的发生。因为电机扭矩变化会直接关系到电机电流的变化,当电机电流意外下降时,电机扭矩也会相应下降。所以本文用电机扭矩参数的变化来反映电机电流的变化。
对系统注入电机电流故障,卫星x轴的电机电流在采样时间为1 500时相对于正常值下降了50%,图6显示了卫星姿态控制系统产生的残差信号。
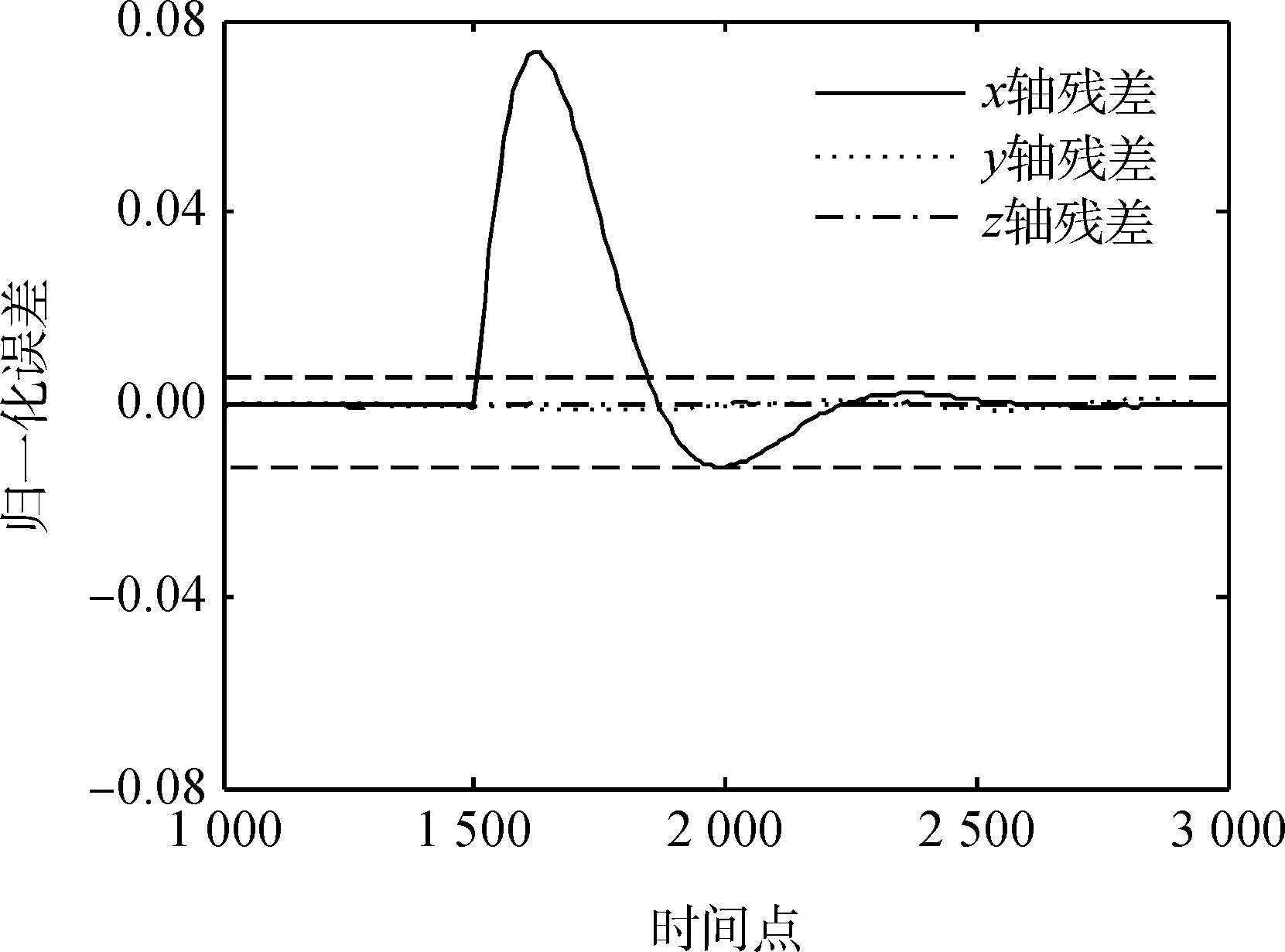
图6 x轴电机电流故障时的三轴姿态残差信号Fig.6 Residual signal of x-axis motor current fault
(2)黏性摩擦导致的温度故障
卫星反作用飞轮中的黏性摩擦一般与黏性扭矩有关,由式(5)可知摩擦扭矩主要取决于其工作环境温度,因此任何的温度变化都会对控制力矩产生影响。当温度很高时,会引起轴承的损坏,从而黏性摩擦会进一步变大。所以,温度故障可能会导致卫星处于非正常运行的状态。
对系统注入黏性摩擦导致的温度故障,卫星z轴的摩擦温度在采样时间为1 500时相对于正常值升高了30%,图7显示了卫星三轴产生的残差信号。
通过同样的方法,分别对x轴、y轴和z轴注入30%~80%的6次电机电流故障和6次温度故障,最终都能够检测出故障的存在,并且在无故障的情况下没有出现虚报故障的情况。通过对提出的两种故障类型进行模拟仿真和检测可以看出,本文所提出的基于Elman神经网络的故障检测系统可以快速有效地检测出单颗卫星姿态控制系统中电机电流故障和黏性摩擦导致的温度故障,并且没有虚惊和漏警的情况出现,表明了提出的方案对于单颗卫星故障检测的精确性和可靠性。
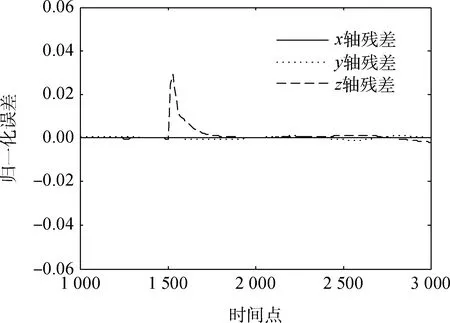
图7 z轴温度故障时的三轴姿态残差信号Fig.7 Residual signal of z-axis viscous temperature fault
3 卫星群姿态控制系统故障诊断
对于卫星群的飞行任务来说,每一颗卫星的故障诊断系统都只能检测到自身发生的故障问题,一旦自身的诊断系统出现故障,就不能继续进行故障诊断任务了。鉴于此,为了提高群飞行任务中故障诊断系统的可靠性,本文提出了分布式卫星群故障诊断系统,采用3颗卫星组成的卫星群系统进行仿真分析。
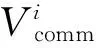
通过这种方法,一旦卫星出现故障问题,卫星群中的相邻卫星也会同时检测到故障的存在,这样就可以进行下一步的故障容错和卫星群的姿态重构任务。

图8 卫星群故障诊断系统的结构Fig.8 Structure of the fault detection system in formation flying
4 仿真试验
本文采用基于虚拟结构的群飞行控制技术[25],3颗卫星位于同一平面并等距离分布在直径为0.5km的圆周上。假设3颗卫星构成的卫星群为一个刚性结构,同时群飞行构型保持不变,并且在机动过程中卫星都保持相对固定的运动方向。通过对系统注入噪声条件下的各种故障参数来判断故障诊断系统的有效性。故障检测过程中,任何偏离阈值范围的残差信号都将被判定为有故障发生。本文将通过对不同故障环境下卫星群x轴姿态系统的仿真试验来证明所提出的故障诊断方法的可实行。
在神经网络训练阶段,改进的Elman神经网络在不同噪声条件下通过蒙特卡洛方法进行步长为0.01s的3 000步仿真。通过2 000次的训练迭代后均方差的平均值为0.007 12,满足性能指标的要求。
对于卫星群姿态控制系统中执行器可能发生的故障问题,通过以下几个案例进行仿真分析,验证所提出的基于虚拟结构的分布式卫星群故障诊断方案的可实性。
(1)电机电流故障
在卫星群的姿态控制系统中,卫星2在x轴中反作用飞轮的电机电流在采样时间为1 500时相对于正常值下降了50%,图9显示了卫星2和卫星1的x轴姿态控制系统中的残差信号。
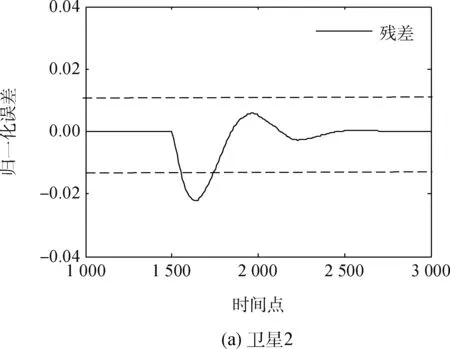
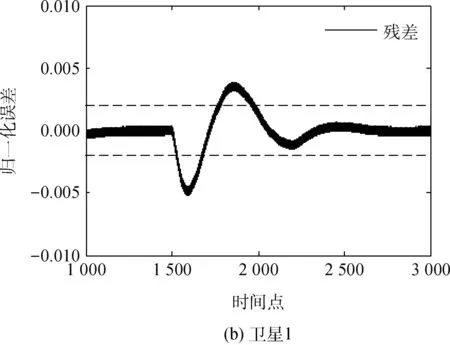
图9 卫星群姿态控制系统中x轴的残差信号Fig.9 Residual signal of x-axis in control system
(2)黏性摩擦导致的温度故障
在卫星群的姿态控制系统中,卫星1中x轴的电机电流在采样时间为2 500时相对于正常值上升了80%,图10显示了卫星1和卫星3姿态控制系统中x轴的残差信号。


图10 卫星群姿态控制系统中x轴的残差信号Fig.10 Residual signal of x-axis in control system
通过以上仿真试验可以看出,针对卫星群系统执行器可能发生的故障问题,本文所提出的分布式卫星群的故障诊断方案的具有有效性和实时性。一旦第i颗卫星出现故障问题,不仅卫星i的故障诊断系统可以在发生故障后的18个仿真步数即0.18s内检测到故障的发生,卫星i-1也能在发生故障后的73个仿真步数即0.73s内诊断出故障的发生。通过同样的方法,对x轴、y轴和z轴采用同样的仿真试验,即分别注入30%~80%的电机电流故障和温度故障各6次,同样也能得到与上述相同的故障诊断结果,都能够诊断出故障的发生,并且没有无故障条件下谎报故障的情况出现。
5 结束语
本文提出了基于Elman神经网络的卫星群姿态控制系统的故障诊断方案,并以反作用飞轮为研究对象进行故障分析和仿真试验。分布式卫星群故障诊断方案能有效地检测出故障卫星,并且临近卫星也能通过Elman神经网络方法检测到故障的发生。试验结果表明,本文提出的故障诊断方案可以使故障卫星在故障发生的第一时间就能被检测出来,临近卫星也能在短时间内检测到该故障,没有发生虚警和漏警的情况出现,基本达到了实时性和准确性的要求。后续研究将针对检测到的故障进行进一步的故障隔离、故障估计和卫星群的姿态重构任务。
References)
[1]LI Z, DUAN Z, XIE L, et al. Distributed robust control of linear multi-agent systems with parameter uncertainties[J]. International Journal of Control, 2011, 85(8):1039-1050.
[2]WANG X, CHENG L. Output-feedback consensus control of linear multi-agent systems: a fixed topology[J]. International Journal of Innovative Computing, Information and Control, 2011, 7(5A), 2063-2074.
[3]CHANG C W, CHEN C L, CHANG Y H, et al. Adaptive fuzzy sliding-mode formation control for second-order multi-agent systems[C]∥International Conference on System Science and Engineering. Taipei,2010:310-314.
[4]SCHARF D P, HADAEGH F Y, PLOEN S R. A survey of spacecraft formation flying guidance and control (part 1): guidance[C]∥American Control Conference, 2003. Denver: IEEE, 2003:1733-1739.
[5]SCHARF D P, HADAEGH F Y, PLOEN S R. A survey of spacecraft formation flying guidance and control (Part 2): control[C]∥American Control Conference, 2004.Boston: IEEE,2004:2976-2985.
[6]CHENG L, HOU Z G, TAN M, et al. Necessary and sufficient conditions for consensus of double-integrator multi-agent systems wth measurement noises[J]. IEEE Transactions on Automatic Control, 2011, 56(8):1958-1963.
[7]HU J, LIN Y S. Consensus control for multi-agent systems with double-integrator dynamics and time delays[J]. Control Theory & Applications,2010, 4(1):109-118.
[8]CHENG L, WANG Y, HOU Z G, et al. A sampled-data based average consensus protocol for double-integrator multi-agent systems with switching topologies and communication noises[C]∥Intelligent Control and Automation. Beijing: IEEE, 2012:886-891.
[9]BARUA A, KHORASANI K. Intelligent model-based hierarchical fault diagnosis for satellite formations[C]∥IEEE International Conference on Systems, Man and Cybernetics,2007.Montreal: IEEE, 2007:3191-3196.
[10]BARUA A, KHORASANI K. Multi-level fault diagnosis in satellite formations using fuzzy rule-based reasoning[C]∥2nd International Symposium on Systems and Control in Aerospace and Astronautics, 2008. Shenzhen: IEEE, 2009:1-6.
[11]MESKIN N, KHORASANI K. Fault detection and isolation of actuator faults in spacecraft formation flight[C]∥2006 45th IEEE Conference on Decision and Control. San Diego: IEEE, 2006:1159-1164.
[12]MESKIN N, KHORASANI K. Actuator fault detection and isolation for a network of unmanned vehicles[J]. IEEE Transactions on Automatic Control, 2009, 54(4):835-840.
[13]MESKIN N, KHORASANI K, RABBATH C A. A hybrid fault detection and isolation strategy for a network of unmanned vehicles in presence of large environmental disturbances[J]. IEEE Transactions on Control Systems Technology, 2010, 18(6):1422-1429.
[14]AZIZI S M, KHORASANI K. A distributed Kalman filter for actuator fault estimation of deep space formation flying satellites[C]∥Systems Conference, 2009 3rd Annual IEEE. Vancouver: IEEE, 2009:354-359.
[15]AZIZI S M, KHORASANI K. A hybrid and switching framework for cooperative actuator fault estimation of formation flying satellites in deep space[C]∥Asian Control Conference, ASCC 2009. Hong Kong: IEEE, 2009:1126-1131.
[16]SHAMES I, TEIXEIRA A M H, SANDBERG H, et al. Distributed fault detection for interconnected second-order systems[J]. Automatica, 2011, 47(12):2757-2764.
[17]SHAMES I, TEIXEIRA A M H, SANDBERG H, et al. Distributed fault detection and isolation with imprecise network models[C]∥American Control Conference (ACC), 2012. Montreal: IEEE, 2012:5906-5911.
[18]VALDES A, KHORASANI K. A pulsed plasma thruster fault detection and isolation strategy for formation flying of satellites[J]. Applied Soft Computing, 2010, 10(3):746-758.
[19]VALDES A, KHORASANI K, MA L. Dynamic neural network-based fault detection and isolation for thrusters in formation flying of satellites[C]∥Advances in Neural Networks-International Symposium on Neural Networks. Wuhan, 2009:780-793.
[20]BIALKE B. High fidelity mathematical modeling of reaction wheel performance[C]∥21st Annual American Astronautical Society Guidance and Control Conference. San Diego, Feb.,1998: 483-496.
[21]ELMAN J L, JEFFREY L. Finding structure in time[J]. Cognitiv Science, 1990, 14(90):179-211.
[22]PHAM D T, LIU X. Neural networks for identification, prediction and control[M].London: Springer London, 1995: 113-116.
[23]ZHANG L Y, GU J J, QIN Z M. Elamn network using simulated annealing algorithm and its application in thermal processes modeling[C]∥International Conference on Machine Learning and Cybernetics, 2007. Hong Kong: IEEE, 2007:929-933.
[24]刘雄峰, 李博, 李俊. 基于遗传算法的 Elman 神经网络模型在大坝位移预测中的应用[J]. 水资源与水工程学报, 2014(3):152-156.
LIU X F, LI B, LI J. Application of Elman neural network model in prediction of dam deformation based on genetic algorithms[J]. Journal of Water Resources and Water Engineering, 2014(3):152-156(in Chinese).
[25]JIANG T, KHORASANI K, TAFAZOLI S. Parameter estimation-based fault detection, isolation and recovery for nonlinear satellite models[J]. IEEE Transactions on Control Systems Technology, 2008, 16(4):799-808.
(编辑:高珍)
Fault diagnosis of reaction wheel in satellite formation
WANG Jiayi,WEN Xin*,ZHANG Wanyi
School of Astronautics, Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
The technology of satellite formation flying is a new technology in the field of space. Multiple low cost small satellites are able to complete more difficult space missions, but at the same time there are more fault diagnosis. Aiming at the problems that the satellite formation may occur in complex space environment,a distributed swarm system of satellites for fault diagnosis method based on Elman neural network was proposed. The experimental results show that the proposed scheme can detect the fault of the reaction wheels, and the adjacent satellite can also detect the faults, which is very good and real time and is effective and feasible in practical application.
satellite formation; neural network; fault diagnosis; attitude control; reaction wheel
10.16708/j.cnki.1000-758X.2016.0048
2016-01-07;
2016-06-04;录用日期:2016-06-30;
时间:2016-08-0214:19:59
http:∥www.cnki.net/kcms/detail/11.1859.V.20160802.1419.002.html
王嘉轶(1992-),男,硕士研究生,wangjiayi312@126.com
闻新(1961-),男,教授, wen_xin2004@126.com,主要研究方向为空间飞行器控制及人工智能应用研究
V19
A
http:∥zgkj.cast.cn
引用格式:王嘉轶,闻新,张婉怡,等.卫星群反作用飞轮的故障诊断方法研究[J].中国空间科学技术, 2016,36(4):24-32.
WANGJY,WENX,ZHANGWY,etal.Faultdiagnosisofreactionwheelinsatelliteformation[J].ChineseSpaceScienceandTechnology, 2016,36(4):24-32(inChinese).
