空间非合作目标惯性参数在轨辨识
2016-11-09孔祥龙李文龙李文峰赵毅
孔祥龙,李文龙,李文峰,赵毅
上海卫星工程研究所,上海 201109
空间非合作目标惯性参数在轨辨识
孔祥龙,李文龙*,李文峰,赵毅
上海卫星工程研究所,上海 201109
在空间冗余机械臂抓捕非合作目标的惯性参数辨识问题中,已有方法大都基于系统动量已知的假设,且辨识过程未考虑基座姿态稳定。针对目标动量未知的问题,设计了具有增量形式的惯性参数分步辨识算法。首先基于线动量方程得到关于质量和质心位置的第一组估计方程,采用增量形式消除未知线动量更新估计方程。辨识结果收敛后根据估计参数计算线动量估计值,代入以转动惯量为未知参数的第二组估计方程中,利用其增量表达式完成对转动惯量的估计。辨识过程中的激励由自适应零反作用控制输入提供,算法在保证基座姿态不受干扰的同时还能对惯性参数精确辨识。仿真结果表明,在30 s以内算法已收敛,误差收敛到零的同时,基座姿态角速率控制精度在10-3以下,说明算法收敛快,精度高,同时还能实现基座姿态稳定。
非合作目标;姿态稳定;冗余自由度;惯性参数辨识;反作用零空间;自适应控制
精确的惯性参数对于航天器控制系统和状态估计系统来说都是非常重要的。以空间机械臂捕获目标为例,当捕获完成后,航天器控制系统必须尽快使组合体稳定下来以执行接下来的任务。如果无法获取组合体航天器的惯性参数信息,控制系统无法精确控制组合体达到期望状态,从而无法完成给定的任务。此外,由于服务航天器必须满足天线对地定向等要求,因此在完成目标捕获后保持服务航天器姿态稳定是非常必要的。
Aghili和Hillenbrand[1-2]采用了基于视觉测量的惯性参数辨识算法。文献[3-4]基于牛顿欧拉方程,采用外部推力作为激励,对惯性参数辨识问题进行了研究。然而,精确测量发动机推力大小和方向是非常困难的。为了解决上述问题,研究人员提出了基于动量守恒方程对惯性参数进行辨识的方法,只需驱动机械臂向任意方向运动,获取不同的测量信息,且只需要对速度进行测量即可。这样一方面可以提高准确性,另一方面还能节省燃料。
Psiaki[5]提出了一种采用总体最小二乘法进行参数辨识的方法,该方法需要对姿态和姿态角速率进行测量,且已经用于实际航天器中。Thienel等[6]提出对航天器惯性参数全部分量进行辨识的自适应方法。Sanyal等[7]在刚体姿态角速度的自适应跟踪问题中讨论了参数辨识方法。Murotsu等[8]考虑了机械臂抓取未知目标后对未知目标进行惯性参数辨识的问题,分别给出了基于动量守恒和牛顿欧拉方程的辨识方法。Yoshida等[9]给出了基于动量守恒的自由漂浮空间机器人的惯性参数辨识方法,考虑了重力梯度力矩,辨识过程无需测量力矩和加速度信息,并在ETS-VII中得到了应用。郭琦等[10]基于动量守恒定律给出了双臂4自由度空间机器人捕捉未知目标的参数辨识问题。田富洋等[11-12]基于动量守恒分别研究了空间单臂和双臂机器人抓取目标时航天器本体和目标参数辨识问题,同时分析了避免方程组奇异的问题。刘宇等[13]考虑空间机器人参数误差问题,基于动量守恒,基于偏差模型的最小二乘法和遗传算法对动力学参数进行了辨识。何光彩等[14]利用前向神经网络辨识了空间机器人本体质量。王洪柳[15]基于最小二乘在线估计目标参数,从线性方程组最小二乘角度分析辨识过程中的参数辨识误差,同时分析了测量噪声对参数辨识的扰动影响。上述基于动量守恒方法的辨识大多假设系统动量为零,与实际情况不符,动量不为零时算法失效,此外辨识过程中未考虑基座姿态稳定要求。
Ma等[16]考虑了动量不为零时的辨识问题,采用了分步法,但只是利用机械臂对航天器本体进行辨识。金磊等[17]在此基础上做了改进,采用了增量形式的辨识方程,提出采用三组测量信息的辨识方法,但未考虑激励问题,且利用测量信息样本少,辨识结果受样本选取方式和测量精度的影响较大。Nguyen等[18-19]提出一种空间冗余机械臂自适应零反作用控制与惯性参数辨识结合的方法,通过在设计控制器中考虑空间飞行器惯性矩阵的变化,达到同时辨识空间飞行器惯性矩阵的目的,但也是基于系统线动量为零的假设的。
本文针对已有研究存在的不足,提出一种同时实现动量未知情况下非合作目标参数辨识和基座姿态稳定控制的方法,给出了算法详细流程。辨识方法基于机械臂动量守恒原理,并以自适应零反作用控制输入为持续激励,采用分步辨识的方法。为了消除未知项的影响,采用辨识方程的增量形式作为新的参数估计方程。算法同样适用于动量已知的情况,具有广泛适用性。
1 机械臂参数辨识方程
图1中SI表示惯性坐标系,S0表示基座航天器本体坐标系,Si表示第i节臂的连体坐标系,原点位于关节处,x轴沿杆向,由铰链i指向铰链i+1,z轴为关节转动轴,y轴右手定则确定。r0为基座质心位置矢量,ai为关节i到杆i质心位置矢量,pi为关节i的位置矢量,ki为关节旋转轴指向矢量,φi为关节角速率,ωt为目标转动角速度矢量。如无特殊说明,文中的所有矢量都需在惯性系中给出。
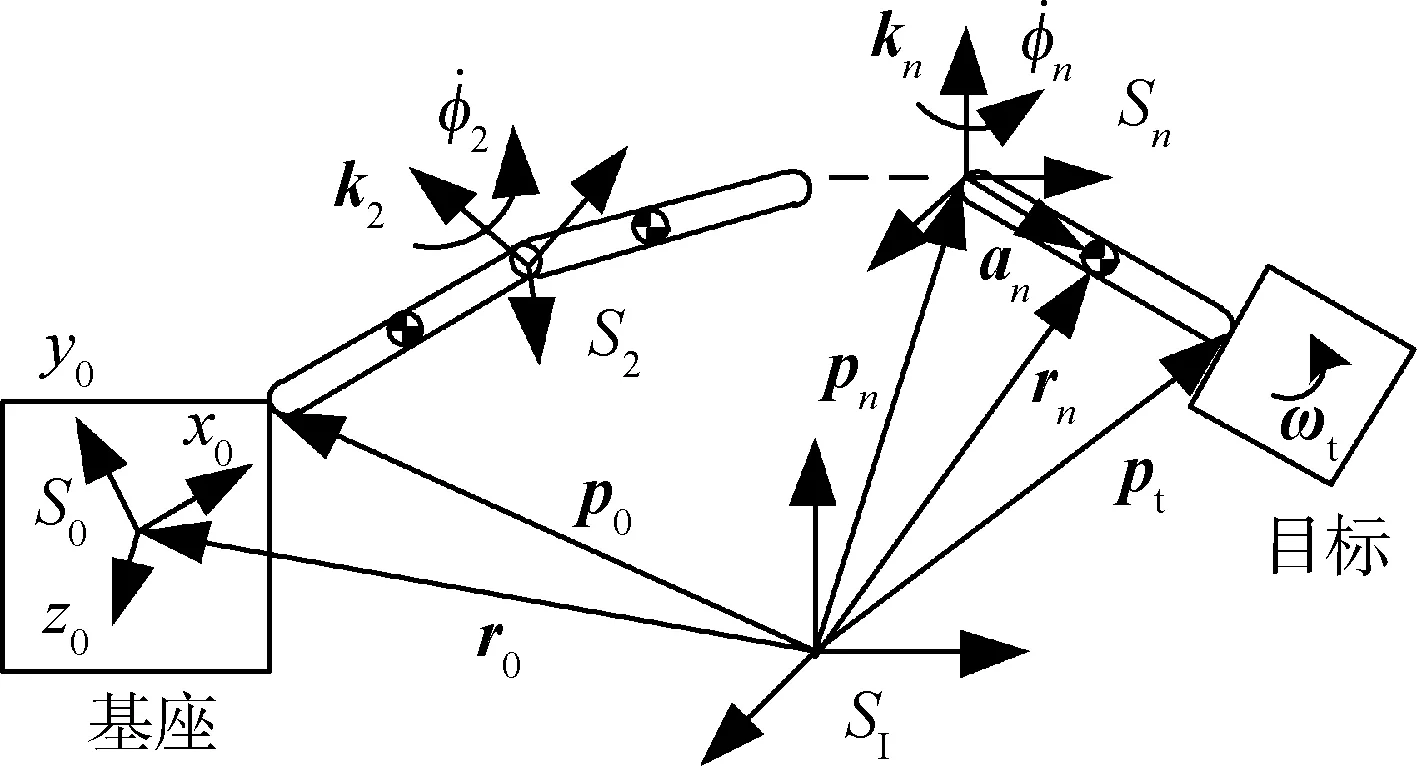
图1 自由漂浮空间机械臂Fig.1 Free-floating space manipulator
本节给出基于动量守恒的参数辨识方程。首先给出如下假设:1)机械臂抓捕目标后末端执行器与目标刚性连接,末节臂与目标成为一个整体,即物体n,因此末节臂惯性参数发生变化;2)组合体除末节臂以外,其余各体的惯性参数都是已知的;3)所有速度信息可通过敏感器测量得到。待辨识参数为新的末节臂的质量mn,质心位置nan,以及关于末节臂质心的转动惯量nIn。上标n表示在坐标系Sn中,下标n表示物体n。
机械臂抓捕目标前,机械臂系统和目标分别具有线动量Pm和Pt以及角动量Lm和Lt,系统总的线动量P=Pm+Pt,总的角动量L=Lm+Lt,由动量守恒得,抓捕目标后系统的线动量和角动量仍为P和L。抓捕后系统动量可分别为两部分,分别为基座与前n-1节臂组成的子系统1的动量以及末节臂子系统2的动量。前者由于可通过测量信息直接获得,也称为可测量部分;后者由于惯性参数是通过估计方法得到的,因此称为估计部分。本文拟采用递推最小二乘方法进行参数辨识。因此,首先要将动量方程写成关于未知参数的线性方程形式。根据上述动量分解方法,系统动量方程可重新写为
(1)
(2)
位置矢量
(3)

(4)
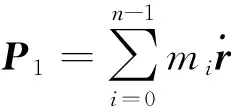
(5)
(6)
其中
由于本文重点验证特殊激励下的辨识算法的可行性以及对任意运动状态系统的适用性,因此式(6)中暂不引入测量误差的影响。
类似地,将式(3)和式(4)代入式(2)中得:
(7)
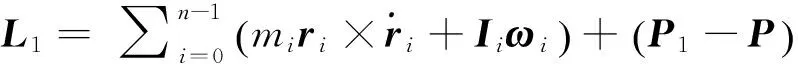
(8)
其中
将式(8)写成矩阵形式:
(9)
其中
式(6)、式(9)共同构成了惯性参数辨识的基本方程。接下来将以这两个方程为基础给出具体的辨识算法。
2 参数辨识算法
2.1增量形式估计方程
在前文的公式推导中已得到形如式(6)和式(9)的辨识方程。从式(6)中的测量矩阵H1中可以看到存在与系统总的线动量P相关的项。同样,在式(9)中,测量矩阵H2中同样包含线动量P,此外在测量值Z2中还存在系统角动量L。机械臂抓捕目标后系统总动量是机械臂动量和目标动量的总和。在实际任务中,Pm和Lm始终可以看做是已知量,对于非合作目标则无法得到Pt和Lt的精确信息,也就无法知道P和L的精确值。以往的研究中大多假设抓捕前后系统的总动量都为0或者为其他已知常数,然后再做进一步处理,而实际上,两者并不能一概而论统一处理。
通过观察式(6)等式两边项可以发现,方程中等式左边所有量都是可测量的,右边项测量矩阵H1中仅P为未知项,因此取式(6)的增量形式以消除该常值项
(10)
其中
符号Δ(·)表示(·)在时间t到t+Δt内的增量。
可以发现,通过选取增量形式的估计方程可以将常值项P消去,由于机械臂始终处于运动状态,因此测量值也是时变的,从而得到了时变的测量矩阵ΔH1和测量向量ΔZ1,构成了新的参数估计方程。
接下来对式(9)做同样处理可得
(11)
其中
从ΔH2和ΔZ2的表达式中可以看出,常值项L已经消去,但是P仍然保留在方程中无法消去。考虑到线动量仅与系统各体质量、质心位置和速度相关,与转动惯量无关,因此这里采用分步辨识的方法。
分步辨识方法的基本思路是先利用式(10)对目标质量和质心位置进行辨识,待参数收敛或者达到给定收敛条件后,依据所得辨识结果和速度测量信息计算系统线动量估计值,然后依据式(11)开始执行转动惯量值的辨识。参数估计方法可以采用文献[20]中给出的递推最小二乘法。
2.2辨识激励问题
文献[21]指出,只有在机械臂的输入运动充分并且持续地给予激励时,参数辨识算法才能收敛到它的精确值。Nguyen-Huynh T C和Sharf I[18-19]针对空间冗余机械臂抓捕空间非合作自旋目标任务,讨论了减小抓捕目标后机械臂运动对基座姿态的干扰的问题,提出了一种自适应零反作用控制算法。该算法基于动量守恒和参数自适应问题中的递推最小二乘法,实现了基座的零反作用控制,且证明了激励的充分和持续性。本文采用这种激励方式,控制律设计过程可参照原文献。需要指出的是,激励的本质是关节处的控制力矩输入,采用的是PD控制方法,属于反馈控制,反馈控制的状态量是关节角和角速度,是动力学方程在系统激励下的输出,二者关系如图2所示。

图2 待辨识参数与辨识激励的关系Fig.2 Parameters to be identified and control input
2.3参数辨识算法流程
至此,整个基于自适应零反控制的惯性参数辨识算法可描述为以下流程:
1)初始化t=0,给定初值X1(0),P(0)=p1I,令t=t+Δt;
2)以自适应控制为输入,仿真计算t时刻关节角速率φ(t)和ω0(t)的值,令t=t+Δt;
3)重复步骤2)得到下一时刻测量值φ(t)和ω0(t);
4)以式(6)为估计方程,依据递推最小二乘算法更新增益矩阵P1(t);
5)递推计算下一时刻估计值X1(t);
6)令t=t+Δt,判断是否满足收敛条件,如满足,转到步骤7),否则返回步骤3);
7)将mn和nan的估值代入式(1)可得线动量P;
8)初始化初值X2(0),P(0)=p2I,t=t+Δt;
9)重复步骤3);
10)以式(9)为估计方程更新增益矩阵P2(t);
11)递推计算X2(t);
12)令t=t+Δt,判断是否满足收敛条件,如满足,算法结束,否则返回步骤9)。
3 仿真算例
图3所示为空间9自由度冗余机械臂抓捕非合作自旋目标示意。基座航天器质量mb=500 kg,转动惯量Ib=diag([83.61 83.61 83.61])kg·m2,尺寸为1×1×1 m3,各杆完全相同,mi=5 kg,i=1,…,9,转动惯量为Ii=diag([0.1 1.5 1.5])kg·m2,杆长0.2 m,目标质量为mt=100 kg,Itxx=Ityy=Itzz=5 kg·m2,Itxy=Ityz=-0.1 kg·m2,Itxz=0.1 kg·m2,尺寸为0.5×0.5×0.5m3。初始时刻基座角速度ω0=[0 0 0]T,线速度v0=[0 0 0]T,各关节转角为0,速度都为0.01 rad/s。初始构型为,臂1、3、5、7、9的连体坐标轴与基座本体系平行,臂2、4、6、8连体系互相平行,且S2为S1绕x轴顺时针转过90°所得。

图3 空间9自由度机械臂Fig.3 9 DOFs space manipulator
末节臂抓捕目标与目标形成组合体后惯性参数的理论值为质量m=105 kg,质心位置rc=[0.433 3 0 0] m,转动惯量Ixx=5.1 kg·m2,Iyy=7.083 3 kg·m2,Izz=7.083 3 kg·m2,Ixy=Iyz=-0.1 kg·m2,Ixz=0.1 kg·m2,采用递推最小二乘估计方法,分别选取初值X10=0,X20=0,选取P10=p1I,P20=p2I,p1=p2=1×105,得到的辨识结果如图4~图7所示。
图4给出的是质量辨识误差,从图中可以看出辨识算法收敛速度非常快,大约在4 s左右参数估计结果收敛,且辨识精度很高,不考虑测量误差情况下质量辨识误差收敛到零。图5为基于动量方程辨识得到的质心位置误差,同样可以看出辨识算法收敛快,辨识精度高。
图6是基于角动量方程辨识得到的转动惯量误差曲线,从图中可以看出,转动惯量达到收敛所需时间更长,但也在25 s左右达到收敛,最后辨识误差都收敛到了零。由此证明本文所给的基于递推最小二乘和基于自适应零反作用控制的惯性参数辨识十分高效且具有高精度,适合实时在线操作。

图4 质量辨识误差Fig.4 Estimation error of mass
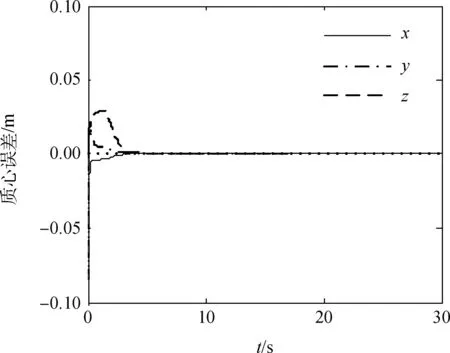
图5 质心位置辨识误差Fig.5 Estimation error of position center of mass
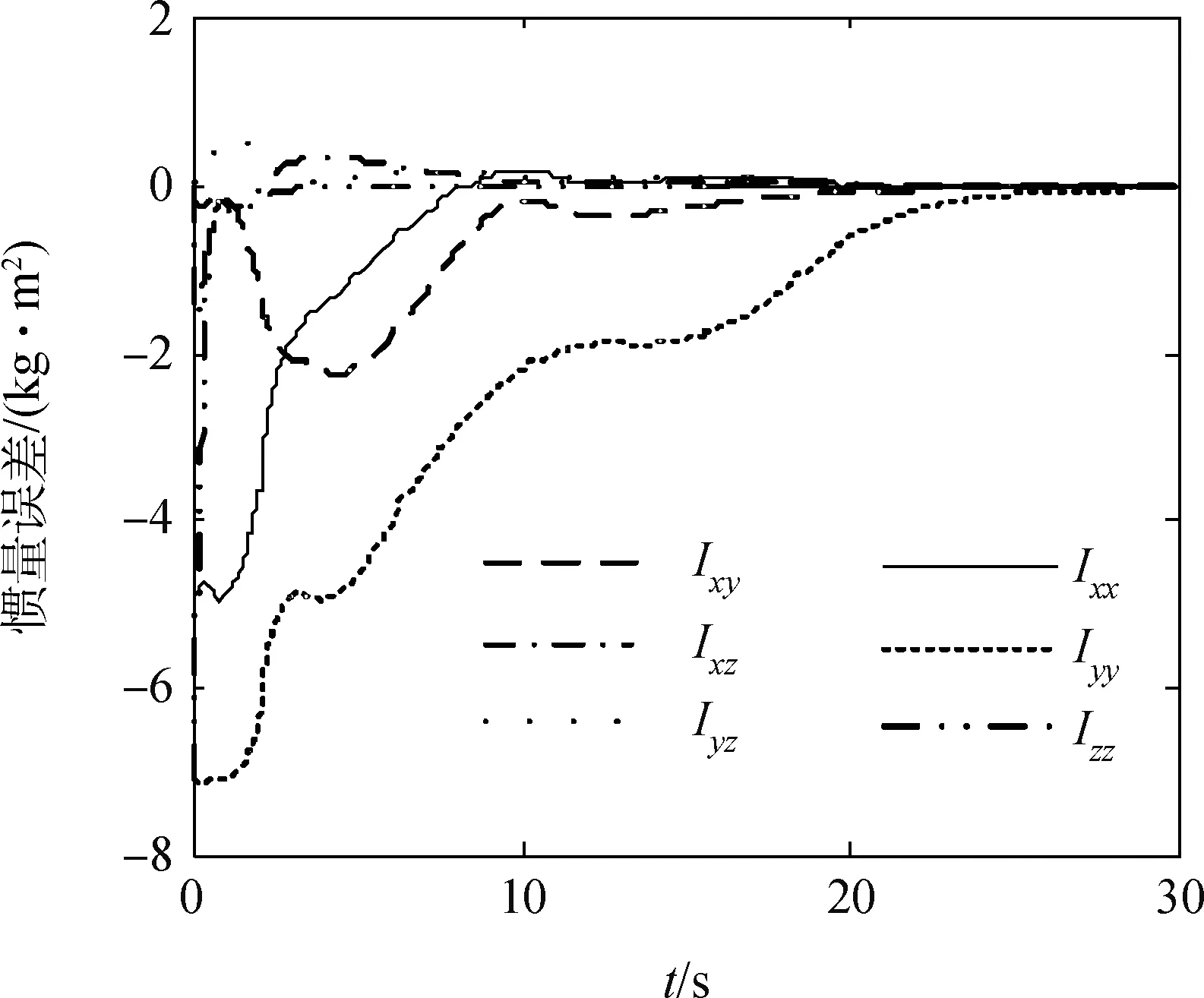
图6 转动惯量辨识误差Fig.6 Estimation error of inertia tensor
为了验证自适应零反作用控制算法,图7给出了基座角速度变化曲线,从图中可以看出,基座姿态角速度量级小于10-3,也即近似为零,这也证明了控制算法的有效性。

图7 基座角速度Fig.7 Attitude angular velocity of base
4 结束语
本文研究了空间冗余机械臂抓捕非合作目标后对未知目标的惯性参数做在轨辨识的算法。将分步辨识法与增量形式的估计方程结合,解决了系统动量未知时的传统基于动量的辨识算法失效的问题。此外,采用自适应零反作用控制输入作为激励,可以保证激励充分而持久。数值仿真结果证明了辨识算法的有效性和快速性,因此适合实时在线操作。仿真结果同时也证明了激励输入下基座姿态响应几乎为零,说明即使原机械臂在抓捕非合作目标后受到了强烈的干扰,但基座姿态依然能够保持稳定,符合实际工程需求。
本文给出的算法是基于测量信息可测且精确的前提下给出的,后续研究将结合实际工程应用,考虑测量可行性和测量精度,开展更进一步研究。
References)
[1]AGHILI F,PARSA K. Motion and parameter estimation of space objects using laser-vision data[J]. Journal of Guidance, Control, and Dynamics,2009,32(2):537-549.
[2]HILLENBRAND U,LAMPARIELLO R. Motion and parameter estimation of a free-floating space object from range data for motion prediction[R]. ESA,2005:461-470.
[3]LAMPARIELLO R,HIRZINGER G. Modeling and experimental design for the on-orbit inertial identification of free-flying space robots[C]∥International Design Engineering Technical Conference & Computers and Information in Engineering Conference. Long Beach,2005.
[4]BERGMANN E,DZIELSKI J. Spacecraft mass property identification with torque-generating control[J]. Journal of Guidance,Control,and Dynamics,1990,13(1):99-103.
[5]PSIAKI M L. Estimation of a spacecraft′s attitude dynamics parameters by using flight data[J]. Journal of Guidance,Control,and Dynamics,2005,28(4):594-603.
[6]THIENEL J K,LUQUETTE,SANNER R M. Estimation of spacecraft inertia parameters[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu,2008.
[7]SANYAL A K,CHELLAPPA M J. Globally convergent adaptive tracking of spacecraft angular velocity with inertia identification and adaptive linearization[C]∥Proceedings of 42nd IEEE Conference on Decision and Control. Maul:IEEE,2003:2704-2709.
[8]MUROTSU Y,SENDA K,OZAKI M. Parameter identification of unknown object handled by free-flying space robot[J]. Journal of Guidance,Control,and Dynamics,1994,17(3):488-494.
[9]YOSIDA K, ABIKO S. Inertia parameter identification for a free-flying space robot[C] ∥AIAA Guidance, Navigation and Control Conference and Exhibit. Monterey, California, USA, August 5-8, 2002.
[10]郭琦, 洪炳镕. 双臂四自由度空间机器人捕捉未知目标的参数辨识[J].机器人, 2005,27(6):512-516.
GUO Q,HONG B R. Parameter identification of unknown object handled by a dual-arm four-degree-of-freedom space robot[J]. Robot, 2005,27(6):512-516(in Chinese).
[11]田富洋,吴洪涛,赵大旭,等. 在轨服务双臂空间机器人的参数辨识[J]. 华南理工大学学报,2010,38(2):73-78.
TIAN F Y,WU H T, ZHAO D X,et al. Parameter identification of on-orbit-servicing dual-arm space robot[J]. Journal of South China University of Technology,2010,38(2):73-78(in Chinese).
[12]田富洋,吴洪涛,赵大旭,等. 在轨空间机器人的参数辨识[J].中国空间科学技术, 2010, 30(1):10-17.
TIAN F Y,WU H T, ZHAO D X,et al. Parameter identification of orbital free-floating space robot[J]. Chinese Space Science and Technology,2010,30(1):10-17(in Chinese).
[13]刘宇,夏丹,李瑰贤,等. 基于角动量守恒的空间机器人动力学参数辨识[J]. 宇航学报, 2010, 31(3):695-700.
LIU Y,XIA D,LI G X,et al. Dynamic parameter identification for a space robot based on angular momentum conservation[J]. Journal of Astronautics,2010,31(3):695-700(in Chinese).
[14]何光彩,洪炳镕,郭恒业. 基于参数辨识的冗余自由飞行空间机器人多臂协调运动规划[J].宇航学报, 2000, 21(1):85-89.
HE G C,HONG B R,GUO H Y. Multi-arm coordinated motion planning of redundant free-flying space robot based on parameter identification[J]. Journal of Astronautics,2000,21(1):85-89(in Chinese).
[15]王洪柳. 空间机器人抓取过程中的目标参数辨识[D]. 哈尔滨:哈尔滨工业大学, 2011.
WANG H L. Parameter identification of target in space robot grasping process[D]. Harbin:Harbin Institute of Technology,2011(in Chinese).
[16]MA O,DANG H,PHAM K. On-orbit identification of inertia properties of spacecraft using a robotic arm[J]. Journal of Guidance,Control,and Dynamics,2008,31(6):1761-1771.
[17]金磊, 徐世杰. 空间机器人抓取未知目标的质量特性参数辨识[J].宇航学报, 2012, 33(11): 1570-1576.
JIN L,XU S J. Inertial parameter identification of unknown object captured by a space robot[J]. Journal of Astronautics,2012,33(11):1570-1576(in Chinese).
[18]NGUYEN-HUYNH T C. Adaptive reactionless motion for space manipulator when capturing an unknown tumbling target[C]∥IEEE International Conference on Robotics and Automation. Shanghai,2011:4202-4207.
[19]NGUYEN-HUYNH T C. Adaptive reactionless motion with joint limit avoidance for robotic capture of unknown target in Space[C].IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura,2012:1155-1160.
[20]刘胜, 张红梅. 最优估计理论[M]. 北京:科学出版社,2011:68-70.
[21]ARMSTRONG B. On find exciting trajectories for identification experiments involving systems with nonlinear dynamics[J]. International Journal of Robotics Research,1989,8(6):28-48.
(编辑:高珍)
Inertia parameter identification of on-orbit uncooperative object
KONG Xianglong,LI Wenlong*,LI Wenfeng,ZHAO Yi
Shanghai Institute of Satellite Engineering,Shanghai 201109,China
Most algorithms of inertia parameters identification assumed the system momentum known and few attention was paid to the attitude stabilization of base. An incremental form of the identification equation was given based on the conservation principle of momentum and a fractional step method was proposed. Firstly, estimation equations about the mass and position of mass center were obtained and the unknown constant linear momentum was eliminated in incremental formulation. The estimate of linear momentum was calculated with the estimated parameters and then substituted into estimation equations about the inertia tensors. The incremental equations were obtained again to eliminate the unknown constant angular momentum. An adaptive reactionless controller was used to persistently excite the robot arm, which guaranteed the convergence of the algorithm as well as the stabilization of base attitude. Simulations results show that inertial parameters are accurately identified and the angular velocities of the base are less than 10-3, which can be viewed as nearly undisturbed.
uncooperative target;attitude stabilization;redundant degree of freedom;inertia parameter identification;reaction null-space;adaptive control
10.16708/j.cnki.1000-758X.2016.0042
2016-01-07;
2016-03-01;录用日期:2016-05-11;
时间:2016-07-1213:26:45
http:∥www.cnki.net/kcms/detail/11.1859.V.20160712.1326.004.html
国家“863计划”(2015AA6301)
孔祥龙(1986-),男,硕士研究生,kxl.longxiao@163.com
李文龙(1988-),男,博士研究生,liwenlongzacao@126.com,主要研究方向为卫星总体设计,在轨服务与维护技术
V43
A
http:∥zgkj.cast.cn
引用格式:孔祥龙,李文龙,李文峰,等.空间非合作目标惯性参数在轨辨识[J].中国空间科学技术, 2016,36(4):17-23.
KONGXL,LIWL,LIWF,etal.Inertiaparameteridentificationofon-orbituncooperativeobject[J].ChineseSpaceScienceandTechnology, 2016,36(4):17-23(inChinese).
