重庆丰都县水天坪工业园区道路高边坡稳定性分析

刘博

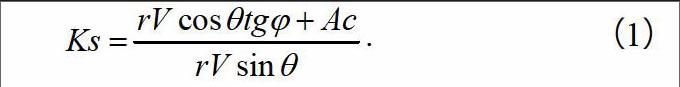
摘 要：近年来，随着我国交通事业的快速发展，高速铁路、高速公路及城市道路等一大批基础设施项目开始实施，各类高边坡问题也随之出现，给工程技术人员带来不少难题。为此，对边坡的稳定性进行了研究，运用2种方法对丰都县水天坪工业园区高边坡进行了稳定性分析。

关键词：道路高边坡；稳定性分析；传递系数法；强度折减法

中图分类号：TU432 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.19.094

1 工程概况

丰都县工业园区Z6道路右侧挖方边坡高12.60～30.20 m，长约为110 m，宽约为25 m，边坡坡顶无建筑物，边坡坡脚为在建Z6道路。右侧边坡开挖后发现边坡顶部前缘出现弧形张拉裂缝，裂缝距离道路中线56～64 m，裂缝最大宽度达到60 cm，裂缝长度达40 m，边坡前缘局部发生滑塌现象。

2 工程地质条件

2.1 地形地貌

项目区地貌单元属于剥蚀浅丘地貌，位于斜坡地带，场地原始地形总体南东高、北西低，地形上为一斜坡，地形坡角较陡，一般为5°～11°，局部地段达35°。场地内地形标高241.02～292.71 m，相对高差51.69 m。

2.2 地层岩性

工程地质测绘及钻探成果表明，项目区分布第四系残坡积粉质黏土（Q4e1+d1）和人工填筑土（Q4me），基岩为侏罗系中统沙溪庙组（J2S）浅黄色、青灰色、灰白色砂岩及暗红色泥岩。

2.3 地质构造

项目区地质构造上位处方斗山冲断背斜北西翼，岩层呈单斜状产出，岩层产状300°∠13°。场内及邻近未发现断层，地层连续。在场地内及邻近基岩露头处测得两组构造裂隙，裂隙发育，其特征分述如下：①组产状272°∠61°，间距0.5～1.8 m，延伸长1.5～5 m，面平直，张开宽1～7 mm，局部存在泥质薄膜，贯通性好，结合差；为硬性结构面。②组产状351°∠79°，间距1.0～2.5 m，延伸长1.2～3.50 m，面平直，张开宽1～3 mm，见褐色铁质氧化膜，结合一般，为硬性结构面。砂岩及泥岩之间接触面分布连续泥化夹层，结合极差，属于软弱结构面。

2.4 不良地质现象

勘察结果表明，边坡区不良地质现象为边坡岩体在施工过程中产生局部开裂或垮塌。

3 用传递系数法进行稳定性分析

3.1 计算模型和计算公式

3.1.1 计算模型

对在建Z6道路右侧边坡，选取3-3′剖面对该段岩质挖方边坡进行稳定性验算。根据边坡的特征及其结构面赤平投影分析，边坡的主要破坏模式为边坡岩体局部沿泥岩及砂岩之间顺层滑移破坏。图1为稳定性计算剖面。

3.1.2 计算公式

边坡的主要破坏模式为岩体局部沿层面滑移破坏，因此采用平面滑动法进行稳定性验算，根据《建筑边坡工程技术规范》（GB 50330—2013），计算公式如下：

式（1）中：r为岩土体的重度，kN/m3；V为岩体的体积，m3；θ为结构面的倾角，°；φ为结构面的内摩擦角，°；A为结构面的面积，m2；c为结构面的黏聚力，kPa。

3.2 计算工况

本次计算时不考虑地震力。

本次计算采用一种工况，即非正常工况。非正常工况为边坡处于暴雨或连续降雨状态下的工况。

3.3 计算参数的确定

计算参数采用反算法确定。根据边坡前缘目前的变形情况，边坡顶部前缘拉裂明显，前缘泥岩块体出现错动痕迹，边坡处于欠稳定状态，在非正常工况下稳定系数取1.02，由于泥岩岩体破碎，结构面结合程度很差，根据《建筑边坡工程技术规范》GB 50330—2013，c值取14.30 kPa，反算求得φ值为11.50°。

3.4 计算结果与评价

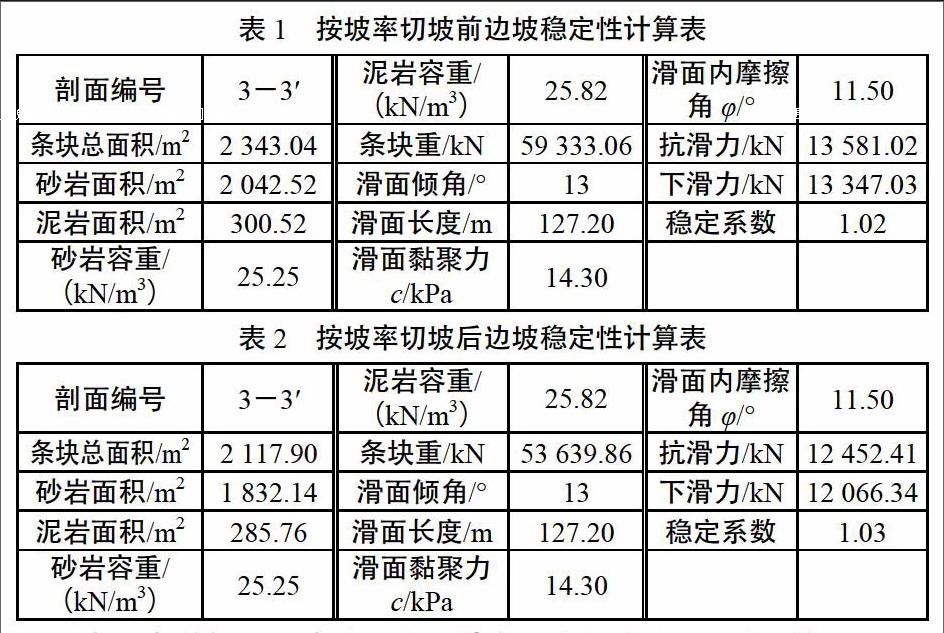
利用理正岩土计算软件6.2版，根据上述计算工况和计算参数设置，计算模型见稳定性计算剖面图，边坡潜在破坏范围根据L=H/tgφ确定。本次计算共包含2项内容，即按边坡切坡前和切坡后2种情况分别计算，计算结果如表1和表2所示。

参照有关规范，边坡稳定性状态划分标准为：稳定系数F≥Fst为稳定，Fst>F≥1.05基本稳定，1.05>F≥1.0为欠稳定，F<1.0为不稳定。其中，Fst为边坡稳定安全系数。根据《建筑边坡工程技术规范》GB 50330—2013，本工程边坡为公路施工边坡，坡顶无重要建筑，边坡安全等级确定为二级边坡，边坡安全系数取1.30.

计算结果：3-3′剖面边坡按坡率切坡前在非正常工况下（暴雨或连续降雨状态下）最小稳定性系数为1.02，边坡欠稳定；边坡按坡率切坡后在非正常工况下（暴雨或连续降雨状态下）最小稳定性系数为1.03，边坡欠稳定。

稳定性验算结果表明，边坡按坡率切坡前和切坡后在非正常工况下均处于欠稳定，必须对该边坡采取工程措施予以处置，以确保施工及行人、车辆安全。

4 用强度折减法进行稳定性分析

传统的极限平衡法能够方便地得到边坡的稳定安全系数，但是无法反映边坡失稳的趋势和过程，采用数值模拟方法正好弥补了这一不足。通过建立边坡有限元仿真模型，不断调整计算参数，从而得到不同的结果，由此可以观察到边坡的变形和失稳发展过程，从而为更好地分析边坡提供一种技术手段。

对于强度折减法计算参数的影响，前人经过研究认为，土体的变形模量和泊松比在采用强度折减法进行有限元分析时对边坡的稳定性系数影响较小，并建议在缺少该参数时可根据经验合理赋值。由于土体材料破坏时一般是剪切破坏，强度指标和内摩擦角是影响边坡安全系数的主要计算参数，其中，内摩擦角的大小直接关系到有限元强度折减法的计算精度，且随着摩擦角的增大，误差也随之增大。此外，在进行有限元计算时，网格的密度和单元尺寸的大小也对计算精度产生不小影响。

根据地勘报告，得到本边坡的岩土体参数，如表3所示。同时，将滑体的计算参数除以折减系数折减，折减后的滑体参数如表4所示。

针对丰都县工业园区Z6道路高边坡，运用传递系数法和强度折减法进行稳定性分析，两者计算结果基本相符。比较2种方法，传递系数法较为直观，能够简单、方便地得出边坡的稳定性系数。

5 结束语

边坡稳定性分析是岩土工程领域的经典课题，也是工程技术人员在工程中常常遇到的问题。本文采用传递系数法和强度折减法对边坡进行了稳定性分析。研究表明，传递系数法和强度折减法都可以作为一种有效的分析手段来指导工程实践，使投资的效益得到提高，同时也对我国工程建设有着重要的意义。

参考文献

[1]陈祖煜.土质边坡稳定性分析：原理·方法·程序[M].北京：中国水利水电出版社，2003.

[2]迟世春，关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报，2004，26（1）.

[3]杨光华，钟志辉，张玉成.用局部强度折减法进行边坡稳定性分析[J].岩土力学，2010，31（2）.

〔编辑：刘晓芳〕