基于ELM运动想象脑电信号的分类

柯海森　双嘉伟

(中国计量学院机电工程学院　浙江 杭州 310018)



基于ELM运动想象脑电信号的分类

柯海森双嘉伟

(中国计量学院机电工程学院浙江 杭州 310018)

针对运动想象脑电信号的分类识别，提出一种基于小波变换和共空间模式滤波的方法进行特征提取。对EEG进行3层小波分解，提取相关层数小波系数的特征量；同时利用共空间模式对EEG进行空间滤波，提取其转换后信号的方差作为特征量，并将这两类特征量进行组合。该方法结合了时频域和空间域的特征信息，可提高分类识别的效果。最后选取BCI2003中Data set Ⅲ数据作为样本，分别用极限学习机和基于粒子群算法的支持向量机进行分类识别。实验结果表明极限学习机分类学习时间较快，最优识别率为94.2857%，证明了该方法更适用于脑机接口系统。

运动想象小波变换共空间模式支持向量机极限学习机

0　引　言

脑机接口BCI(Brain Computer Interface)技术是一种通过大脑与外界环境进行交流控制，使人们可以通过大脑来表达自己的意愿或者控制意图。其主要目标是加强有严重身体缺陷和交流障碍的伤残人士与外界交流和沟通的能力[1,2]。

特征提取和分类器设计是BCI系统中的核心技术，快速准确地对EEG进行分类识别是BCI系统的重要指标。早期的脑电信号特征提取方法有单一类信息法[3]和时频特征组合法[4]可以简单有效提取EEG的特征信息，但该方法处理短信号时特征信息不明显，并且如果信号发生突变时，其提取的特征信息效果不佳；自回归AR(Auto regression)模型[5]虽然能很好地分析出信号的时变特性，但是信号的长度决定其分辨的效果，也不利于短信号的分析；自适应自回归AAR(Adaptive auto regression)模型[6]可以有效地弥补AR模型在短信号处理时的缺陷，但此方法更适用于平稳信号，而EEG是一种非平稳无周期的信号；小波分析[7]可以提取低频时的频率信息和高频时的时间信息，能够很好地分析非平稳信号，但是该方法只考虑了时频域的特征，没有考虑运动想象脑电信号空间域的特征信息。

针对此问题，本文提出一种基于小波变换和共空间模式CSP(Common spatial pattern)的方法，小波变换对EEG进行小波分解，提取相关层数的频域信息作为一组时频域的特征量；同时，对脑电信号进行共空间模式滤波，计算出滤波后信号的方差作为一组空间域的特征向量。组合两组特征量，即对时频域的特征量进行增广，该方法结合了时频域和空间域的特征信息，可提高分类识别的效果。

对于分类器的设计，支持向量机(SVM)主要是对特征量进行升维和线性化，而升维增加计算量使训练学习时间较长；极限学习机(ELM)是一种泛化的单隐层前馈神经网络，但ELM不用计算出每个隐层的连接权值和阈值，而是根据概率论知识随机每个隐层的连接权值和阈值，有效地减少了计算量，极大地缩短训练学习时间。因此，本文选择ELM对特征量进行分类。

而对在线脑机接口系统来讲，能够更快、更高效地实时分类识别出操作人员的脑电信号，是该技术发展的重点方向。本文选用2003年BCI竞赛中的运动想象脑电数据(Data set Ⅲ)，比较了不同特征提取方法的识别效果，在分类算法上对比了ELM和基于粒子群算法的支持向量机(PSO-SVM)的分类效果。实验结果表明本文提出的方法，比只单独使用一种方法的识别率要高，ELM在分类时的学习时间更快，最优识别率为94.2857%也优于PSO-SVM，验证了该方法能更好地应用于BCI实时系统。

1　脑电特征提取方法

1.1离散小波变换

小波变换的实质是通过改变小波窗口的大小，对信号进行多尺度分析，从而实现对信号高频处进行时间细分，而对信号的低频处进行频率的细分。

设x(n)是脑电采集设备输出的离散信号，采用Mallat算法，按式(1)对EEG进行小波分解[7,8]：

(1)

1.2共空间模式滤波

CSP是一种针对多类信号的处理手段，从多类信号集中提取特定的任务信号，并使两者在空间能量的分布差异最大化[9]。

设脑电信号采集设备上共有M个通道，即M个电极，每一次实验每个通道分别采集N个信号，故每次采集的数据可以看成一个M×N的就矩阵Ei。则Ei的标准空间协方差矩阵可以表示为：

(2)

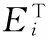
C=Cl+Cr

(3)

而C又可以写成C=BλBT，式中B为C的特征向量矩阵，λ是由非零特征值组成的对角阵。使λ按照对角线上的元素进行递减排列，同时B与之对应的进行调整。求出白化矩阵：

(4)

则矩阵PCPT的特征值为1，又因为式(3)，所以可以令：

Sl=PClPTSr=PCrPT

(5)

则Sl与Sr具有共同的特征向量。可以设：

Sl=DλlDTSr=DλrDTλl+λr=I

(6)

式中，Sl与Sr的共同特征向量D，I是单位阵。由式(6)可知，若λ1是由大到小排列，则λ2是从小到大排列。为了实现两类任务在空间排布的最大差异化，选取λ1中m个最大特征值对应的特征向量和m个最小特征值对应的特征向量，组成新的特征量Dl和Dr来构造两类任务的空间滤波器：

(7)

则每次实验采集的脑电数据Ei,进行共空间模式滤波得到Zi，即Zi=WEi。

2　极限学习机

2.1单隐层前馈神经网络

设训练集共有N个样本，样本的输入集X和输出集T用矩阵表示为：

X=[x1,x2,…,xN]T=[t1,t2,…,tN]

(8)

则标准的单隐层前向神经网络数学模型可以表示为:

(9)

式中，xj和tj表示第j个样本的输入和输出，ai是输入神经元与第i个隐层节点的连接权值，bi为第i个隐层节点的偏置，βi是第i个隐层节点与输出神经元的连接权值，g(x)是无限可微的激励函数。

式(9)式可表示为：

Hβ=T

(10)

H(a1,…,aL,b1,…,bL,x1,…,xN)

(11)

(12)

式中，H为神经网络的隐层输出矩阵。

2.2极限学习机原理

极限学习机的主要原理[10]是：为了达到确定网络结构的目的，可以通过拟合N个不同样本的输入输出来得到任意小的非零误差，并根据实际情况选择L(L≤N)个隐层节点。通过随机每个隐层节点的输入权值ai和偏置阈值bi，来求出隐层输出矩阵H。

当激励函数g(x)无限可微时，只要在训练样本前随机这两个参数，并且在整个训练过程保证两个参数的大小不变，即可以得到输出连接权值。求出式(13)的最小二乘解：

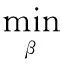
(13)

可求出：

β=H+T

(14)

式中，H+是H的广义逆。

综上，ELM的算法内容如下：

若已知N个训练样本中的输入集和输出集，极限学习机的隐层节点数L，以及无限可微的激励函数g(x)，具体步骤如下：

(1) 随机选取每个隐层节点对应的输入权值ai和隐层偏置bi，i=1，2,…，L；

(2) 通过式(11)确定隐层输出矩阵H；

(3) 通过式(14)求出输出权值β。

3　实验数据

本文选用的数据是Graz大学提供的BCI 2003运动想象脑电数据(Data set Ⅲ)[11]。该实验对同一受试者进行了7×40次实验，每组实验在同一天完成，每次实验后都有一定的休息时间。脑电采集设备使用双级导联的方式，对运动想象区域的C3、C4和Cz三个位置进行脑电信号采集，电极位置如图1所示。

图1　电极位置图

每次实验的时序如图2所示，实验分为三个阶段：0～2 s为等待休息时间；2～3 s屏幕中央出现十字符号提醒受试者做好准备；3～9 s屏幕上随机出现一个向左或者向右的指示箭头，要求受试者按照箭头方向做出与之对应的运动想象。每组实验的采样频率为128 Hz，且每组数据都进行了0.5～30 Hz的带通滤波。比赛共提供了280组数据，140组已知想象运动方式当作训练集，另外140组未知其想象运动方式当作测试集。

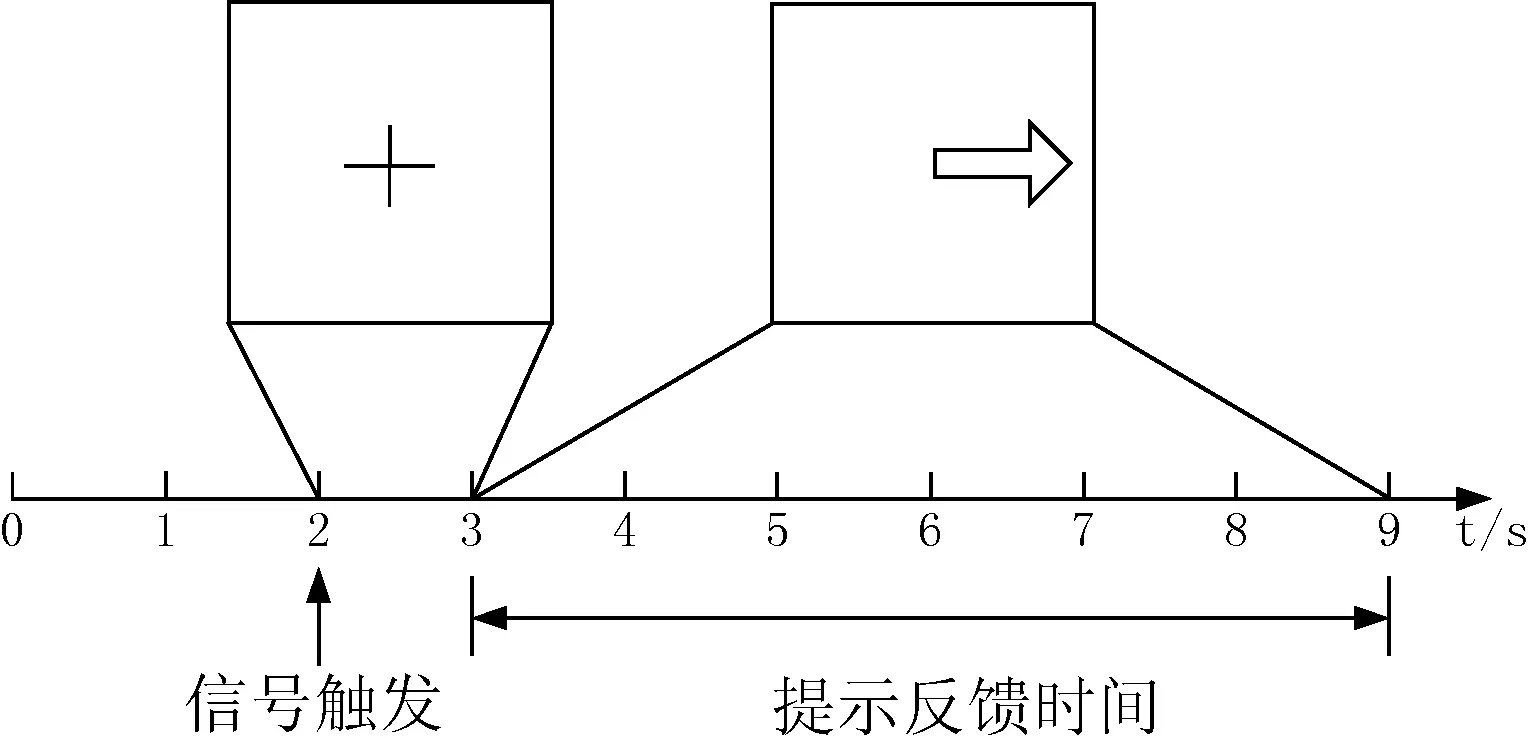
图2　实验时序图

4　数据分析与结果

4.1数据预处理

通过大量的实验证明，人们在想象或实施单侧手运动时，其对侧运动感觉区的μ节律(8～13 Hz)和β节律(18～30 Hz)的幅值降低，此现象称为事件相关去同步ERD(event-related desynchronization)；对应的同侧运动感觉区的μ节律和β节律的幅值升高，此现象称为事件相关同步ERS(event-related synchronization)[7]。所以，本文通过分析想象左右手运动时ERD/ERS信号最明显的EEG信号段，选取合适的时间段进行后续的特征提取及分类。由于，电极Cz的位置与运动想象功能区没有太大的相关性，本文只对C3和C4两个通道采集的数据进行特征提取。首先对140个训练集样本进行8～30 Hz带通滤波，然后按照以下公式计算各导EEG信号的平均能量：

(15)

式中，N为训练集的数量，x(i, j)为第i个样本中第j个采样脑电信号的电压幅值，P(j)为第j个采样脑电信号的平均能量值。通过式(15)得出C3和C4记录的EEG通过8～30 Hz带通滤波后的平均能量变化曲线，如图3所示。

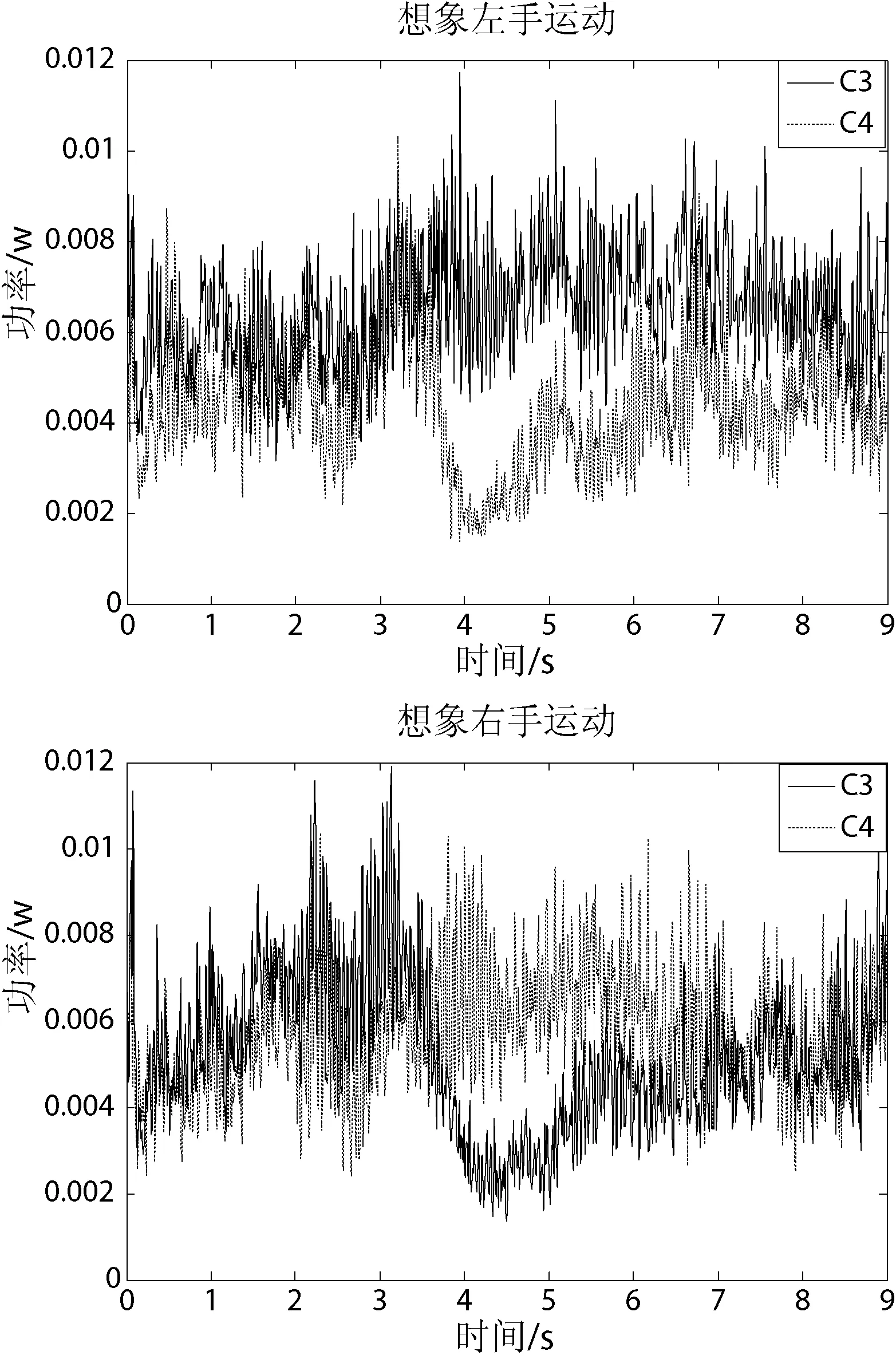
图3　想象左右手运动时C3和C4通道EEG信号的平均能量变化

由图3可得，受试者在9 s的运动想象实验中，其出现ERD现象最明显的是3.5～7 s这个范围内。因此，本文选取3.5～7 s时间段内且频率在8～30 Hz的信号进行后续的特征提取和分类。

4.2特征提取

4.2.1离散小波变换的脑电信号特征提取

因为，小波变换对EEG进行有限层分解，其分解的层数与脑电设备的采样频率和μ节律与β节律所在的频率段有关。本实验脑电采集设备的采样频率为128 Hz，ERD有用成分的信号在8～30 Hz的范围内。因此，本文选用小波db4对EEG进行三层分解，EEG分解后细节部分为D1、D2和D3，近似部分为A3，如图4所示。

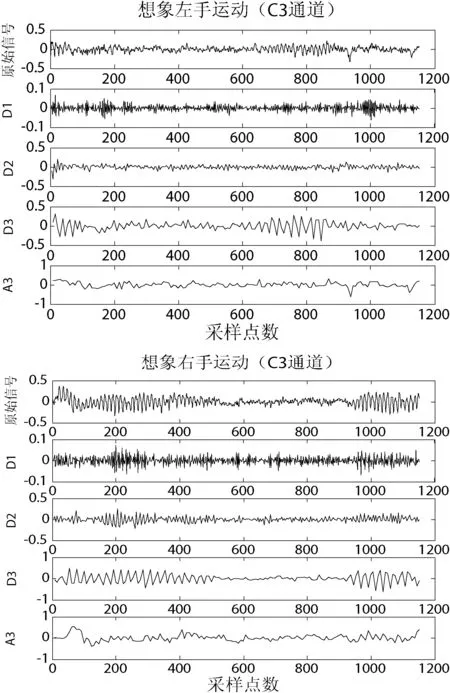
图4　想象左右手运动时小波3层分解(C3通道)

对EEG进行小波3层分解，如表1所示。

表1　小波分解后各层频带范围

由表1可知，μ节律和β节律主要包含在D3和D2这两个细节信号中，因此本文提取D2和D3系数的绝对值的平均值、标准差和能量均值作为一组特征量。

4.2.2CSP的脑电信号的特征提取

通过组合空间协方差矩阵求出的两类空间滤波器Wl和Wr，令W=[Wl;Wr]。通过组合后的空间滤波器W，对实验数据进行滤波，滤波后的部分数据如图5所示。

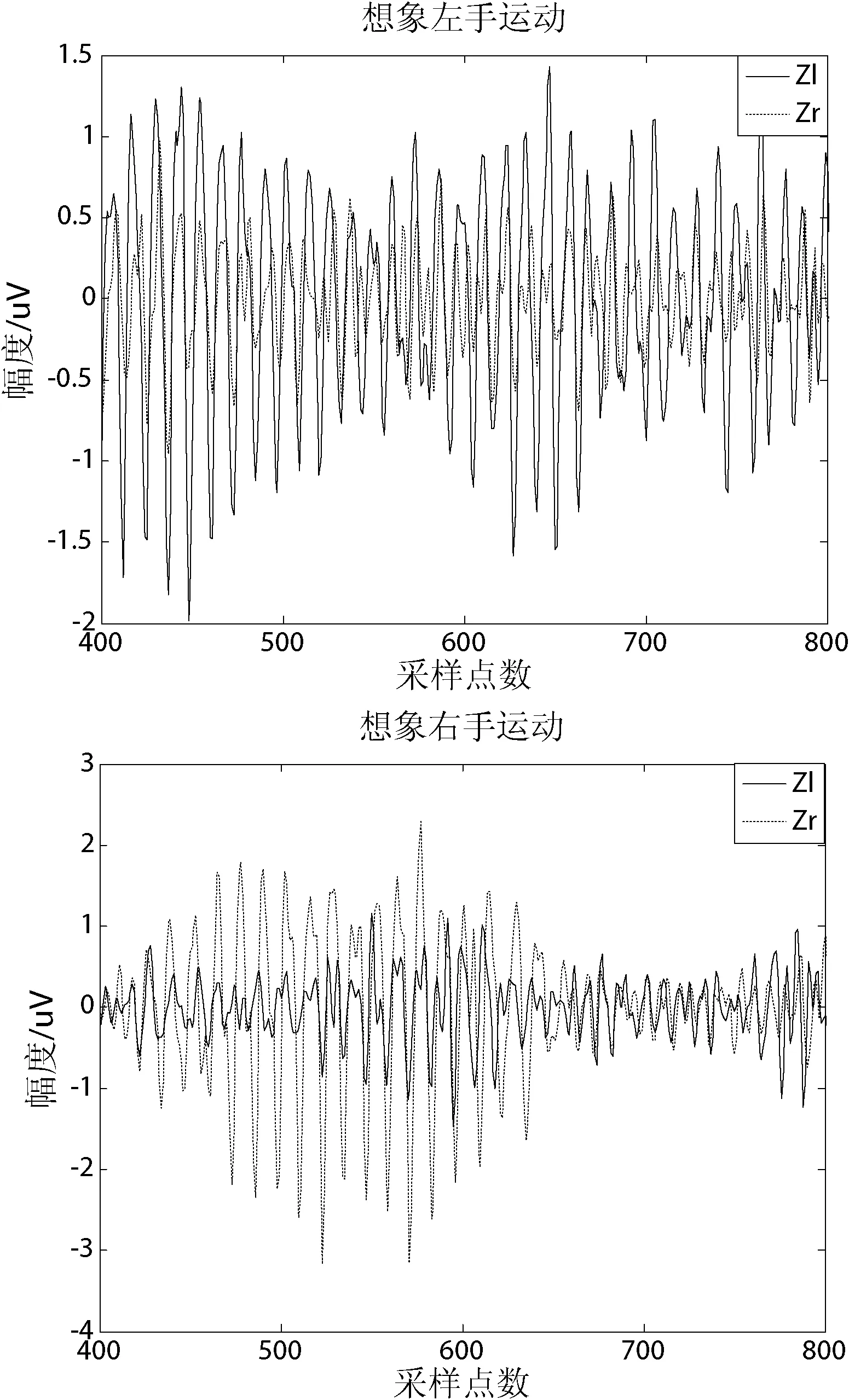
图5　想象左右手运动时信号通过滤波器W

对变换后的信号Zi(i=1,2，…,2n)按式(16)进行变换作为另一组特征量。

(16)

4.3脑电信号分类

通过小波分析和CSP对脑电信号提取的14维特征向量，送入以Sigmoid为激励函数的ELM分类器进行分类识别。为了证明ELM更加适用于运动想象脑电信号的分类，本文通过与使用粒子群算法PSO来寻找最优的C(惩罚因子)和σ(核参数)的SVM分类方法作比较，如表2和表3所示。

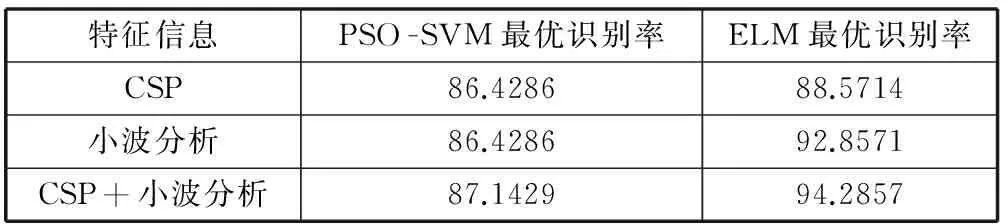
表2　分类准确率的比较

表3　学习时间的比较

通过表2可知，ELM对3种不同特征信息的最优识别率与PSO-SVM相比，分别提高了2.1428%、6.4286%和7.1428%。CSP和小波分析的结合也比只单独提取CSP的特征量和小波分析的特征量的分类识别率高，最优识别率提高了5.7143%。

通过表3可知，ELM的学习分类时间与PSO-SVM的学习分类时间相比，有着很大程度的减小。证明了ELM在运动想象脑电信号的分类中具有更高的分类识别能力，更短的分类学习时间，能够更好地满足BCI实时系统的要求。

同时，将本文的分类结果与BCI 2003的优胜者进行对比，比赛前3名的最优识别率分别为89.29%、84.29%、和82.86%，通过对比可知本文所述方法的最优识别率94.2857%也比第一名的89.29%提高了4.9957%。同时，也比文献[12]的90.71%和文献[13]的92.14%有了明显的提高。

5　结　语

通过对不同的特征量进行分类比较，发现结合频域和空间域的信息都比提取单一类信息的效果好。对比了ELM和PSO-SVM两种分类器的效果，通过实验证明ELM具有更快的学习时间，分类效果也有一定幅度的提高。同时后续的工作研究中，也将对本文提出的运动想象脑电信号分类方法用于在线BCI系统，进行更深入的研究。

[1] Gao Shangkai,Wang Yijun,Gao Xiaorong.Visual and auditory brain-computer interfaces[J].IEEE Transactions on Biomedical Engineering,2014,61(5):1436-1447.

[2] Li X,Wang Y R,Song J L,et al.Research on classification method of combining support vector machine and genetic algorithm for motor imagery EEG[J].Journal of Computational Information Systems,2011,7(12):4351-4358.

[3] Esposito M,Carotenuto M.Intellectul disabilities and power spectra analysis during sleep:a new perspective on borderline intellectual functioning[J].Journal of intellectual disability research,2014,58(5):421-429.

[4] Thanh Nguyen,Khosravi Abbas,Creighton Douglas,et al.EEG signal classification for BCI applications by wacelets and interval type-2 fuzzy logic systems[J].Expert Systems With Applications,2015,42(9):615-624.

[5] Han M,Sun L L.EEG signal classification for epilepsy diagnosis based on AR model and RVM[C]//2010 International Conference on Intelligent Control and Information Processing.DaLian,Liaoning,China:Wang Jun,Han Min,2010:134-139.[6] Hsu Weiyen.Embedded prediction in feature extraction:Application to single-trail EEG discrimination[J].Clinical EEG and Neuroscience,2013,44(1):31-38.

[7] Rosso O A,Martin M T,Figliola A,et al.EEG analysis using wavelet based information tools[J].Journal of Neuroscience Methods,2006,153(2):163-182.

[8] 赵建林,周卫东,刘凯,等.基于SVM和小波分析的脑电信号分类方法[J].计算机应用与软件,2011,28(5):114-116.

[9] Tomida Naoki,Tanaka Toshihisa,Ono Shunsuke,et al.Active data selection for motor imagery EEG classification[J].IEEE Transactions on Biomedical Engineering,2015,62(2):458-467.

[10] Vong Chi Man,Tai Keng Lam,Pun Chin Man,et al.Fast and accurate face detection by sparse Bayesian extreme learning machine[J].Neural Computing & Appplications,2015,26(5):1149-1156.

[11] Blankertz B,Muller K,Curio G,et al.The BCI Competition 2003:Progress and Perspectives in Detection and Discrimination of EEG Single Trials[J].IEEE Transactions on Biomedical Engineering,2004,51(6):1044-1051.

[12] 王月茹,李昕,李红红,等.基于时-频-空间域的运动想象脑电信号特征提取方法研究[J].生物医学工程学杂志,2014,31(5):955-961.

[13] 徐宝国,宋爱国,费树岷.在线脑机接口中脑电信号的特征提取与分类方法[J].电子学报,2011,39(5):1025-1030.

CLASSIFICATION OF MOTOR IMAGERY ELECTROENCEPHALOGRAM BASED ON ELM

Ke HaisenShuang Jiawei

(CollegeofMechanicalandElectricalEngineering,ChinaJiliangUniversity,Hangzhou310018,Zhejiang,China)

In this paper, a proposed method has been introduced to classify the motor imagery EEG, whose features are extracted by using discrete wavelet transform and CSP. The EEG signal is decomposed to three levels and the statistics of wavelet coefficients of correlative level are calculated. Meanwhile, CSP is applied to EEG for space filtering and the variance of converted data is extracted as the features vector. Then the two characteristic quantities are combined. This method combines the features of frequency domain and spatial domain to improve the recognition performance. Finally, using Data set Ⅲ from BCI2003 as the sample to classify this method by using extreme learning machine and support vector machine which is based on particle swarm algorithm. The classification results show that the ELM needs less time to classify and the method obtains the best recognition accuracy at 94.2857, which proves the method is more adaptable to brain computer interface system.

Motor imageryWavelet TransformCommon spatial patternsSupport vector machineExtreme learning machine

2015-07-22。浙江省自然科学基金项目(LY12F030 13)；“十二五”浙江省高校重中之重学科-仪器科学与技术学生开放实验项目(JL150527)。柯海森，副教授，主研领域：自适应控制。双嘉伟，硕士生。

TP391.4R318.04

A

10.3969/j.issn.1000-386x.2016.10.041