一类基因调控模型的稳定性与Hopf分支分析

曹建智，鲍俊艳，周檬

(1.河北大学 数学与信息科学学院，河北 保定　071002；2.河北软件职业技术学院 信息工程系，河北 保定　071000)



一类基因调控模型的稳定性与Hopf分支分析

曹建智1，鲍俊艳1，周檬2

(1.河北大学 数学与信息科学学院，河北 保定071002；2.河北软件职业技术学院 信息工程系，河北 保定071000)

利用中心流形和正规型理论研究了一类由常微分方程组来刻画的基因调控模型，得到该系统局部稳定性和出现Hopf分支的一些充分条件，通过数值模拟验证了所得结论的正确性.

基因调控模型；平衡点；稳定性；Hopf分支

MSC 2010:34C11；34K35

基因调控网络是当今生物数学研究的前沿，主要以孟德尔遗传法则为依据，以基因之间相互作用关系为研究内容，从微观角度揭示复杂的生命现象．基因的表达是相互影响的，一个基因的表达会受另一个基因表达的影响，同时此基因的表达也会影响到另一个基因的表达.基因调控网络模型是把网络中相互作用元素的实验结果和假设转换为数学问题，并利用模型分析、求解等过程得到的理论来帮助了解细胞的动态行为，甚至为了解生物机体的分化和演变提供思路．

迄今为止，用于研究基因调控网络的模型很多，如离散的Boolean网络模型、基于微分方程的连续模型，随机模型等.Boolean等网络模型把基因的表达离散成单一的2个数值0和1，实际上基因表达是连续的，整个网络是这些连续表达值来推动调控的，从而利用微分方程能更加精确地刻画所研究的调控系统,另一方面，大量关于常微分方程与动力系统理论知识可以直接应用到所研究的模型．国内外的学者对于基因调控模型的分析和研究都是高度重视的，研究成果也层出不穷[1-5]，但是到目前为止大部分工作都是针对时滞微分方程的，而完全由常微分方程来刻画的2个基因相互调控的模型还不常见.

本文主要研究的是一类由常微分方程组来刻画的基因调控模型，通过对系统在正平衡点特征方程的分析，得到该系统局部稳定性和出现Hopf分支的一些充分条件，最后通过数值模拟验证了所得结论的正确性.

1　预备知识

考虑如下含参数μ的二维系统

(1)

其中f1,f2∈Cr(r≥1),f1(0,0,μ)=f2(0,0,μ)≡0.

上述定理通常称为Hopf分支定理. 把平面系统(1)在原点Taylor展开至三次项，则令

b102(a11a02+2a02b02)-2a10b10(b022-a20a02)-2a10a01(a202-b20b02)-

(2)

a012(2a20b20+b11b20)+(a01b10-2a102)(b11b02-a11a20)]-

(a102+a01b10)[3(b10b03-a01a30)+2a10(a21+b12)+(b10a12-a01b21)]},

其中aij、bij(i=0,1,2,3;j=0,1,2,3)为相应的系数.则当σ>0时，分支周期解是不稳定的，当σ<0时，分支周期解是稳定的(详见文献[7]).

2　一类基因调控模型的局部稳定性与Hopf分支分析

本节要讨论的基因调控模型如下：

(3)

其中x和y分别表示基因1和2调控因子的浓度，r表示基因在没有调控因子时的基本合成率，l1和l2表示降解率，p是x的分解常数，q是y的分解常数，k1为x的最大转录率，k2为x的最大合成率，以上参数均为正数(模型的详细介绍见文献[8]).

2.1模型正平衡点的存在性

要求出这个方程组所有可能的平衡点，需令式(3)的右端2个方程都等于0，即

(4)

把式(4)的2个方程移项后相除并用x表示y，有

(5)

将表达式(5)代入式(4)的第1个方程中，得

(6)

进一步推导得

x3+Ux2+Vx+R=0,

(7)

其中

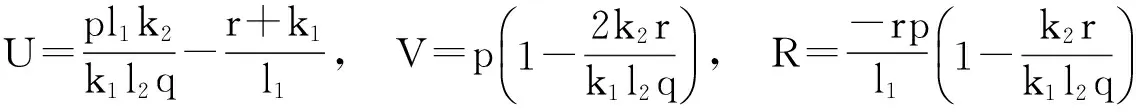
方程(7)两端对x求导得

3x2+2Ux+V=0.

考虑到模型的生物意义，本文仅对系统(3)的正平衡点进行研究.下面的引理保证了在一定条件下系统(3)存在唯一的正平衡点.

1)Δ=U2-3V≤0；

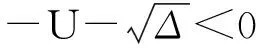
注：从数学的观点来看，系统(3)的平衡点在不同条件下存在的个数也不相同，引理1为存在唯一正平衡点的一种特殊情况.如，当式(7)有2个或3个正根时，系统(3)正平衡点的个数分别为2个或3个，此时系统(3)的稳定性及分支情况较为复杂，这是未来研究的重点.

2.2平衡点的稳定性与Hopf分支

(8)

其中

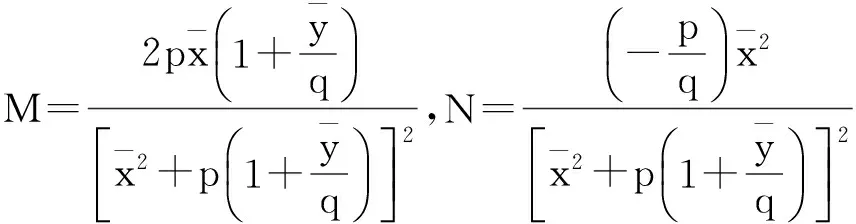
导算子矩阵为

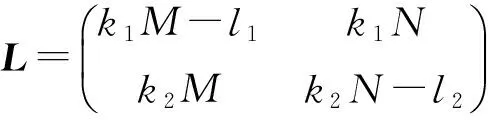
系统(8)的特征方程为

(9)

众所周知，β0和β1的符号在研究式(3)的局部性质时起着决定性作用.对于β0，可以证明它是大于0的.事实上，将式(5)代入式(4)中的第1个方程得

(10)

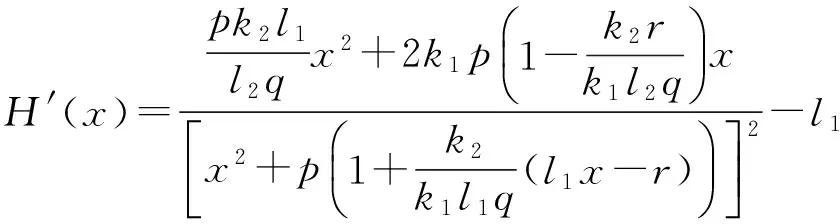
定理2在β0>0的情况下，如下结论成立:

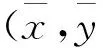
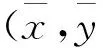
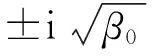
下面讨论系统(3)是否出现Hopf分支.

下面研究分支周期解的一些性质.首先需要把系统(3)的平衡点平移到原点，并在原点处进行Taylor展开得

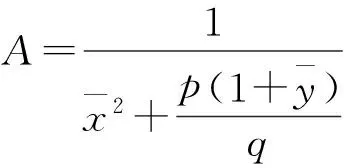
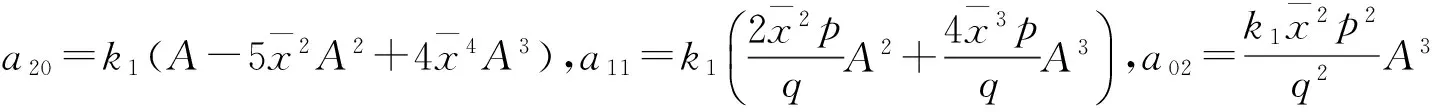
o(u3,v3)为u3、v3的高阶无穷小.把aij(i=0，1，2，3；j=0,1,2,3)中的k1换成k2即为bij(i=0，1，2，3；j=0,1,2,3).

由预备知识，理论上可以计算出决定分支周期解稳定性的第一Lyapunov指数σ，但本文中σ的表达式太复杂，很难判断σ的符号，在下边的例子中将给出具体参数σ的符号.

3　数值例子

用与文献[4]相同的参数对所得结论进行数值模拟.令l1=1，l2=0.2，k2=0.4，p=10，q=5，r=0.4，则基因调控模型(3)变为

(11)

另外，根据公式(2)可计算出系统(11)的第一Lyapunov指数为σ=-349 2.234 5π<0，所以分支周期解是稳定的.

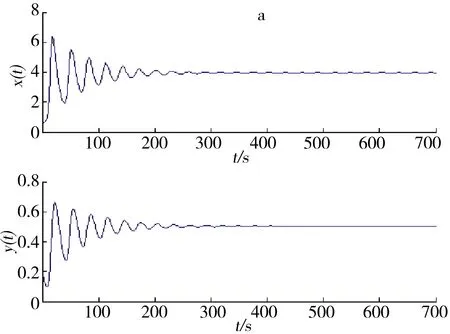
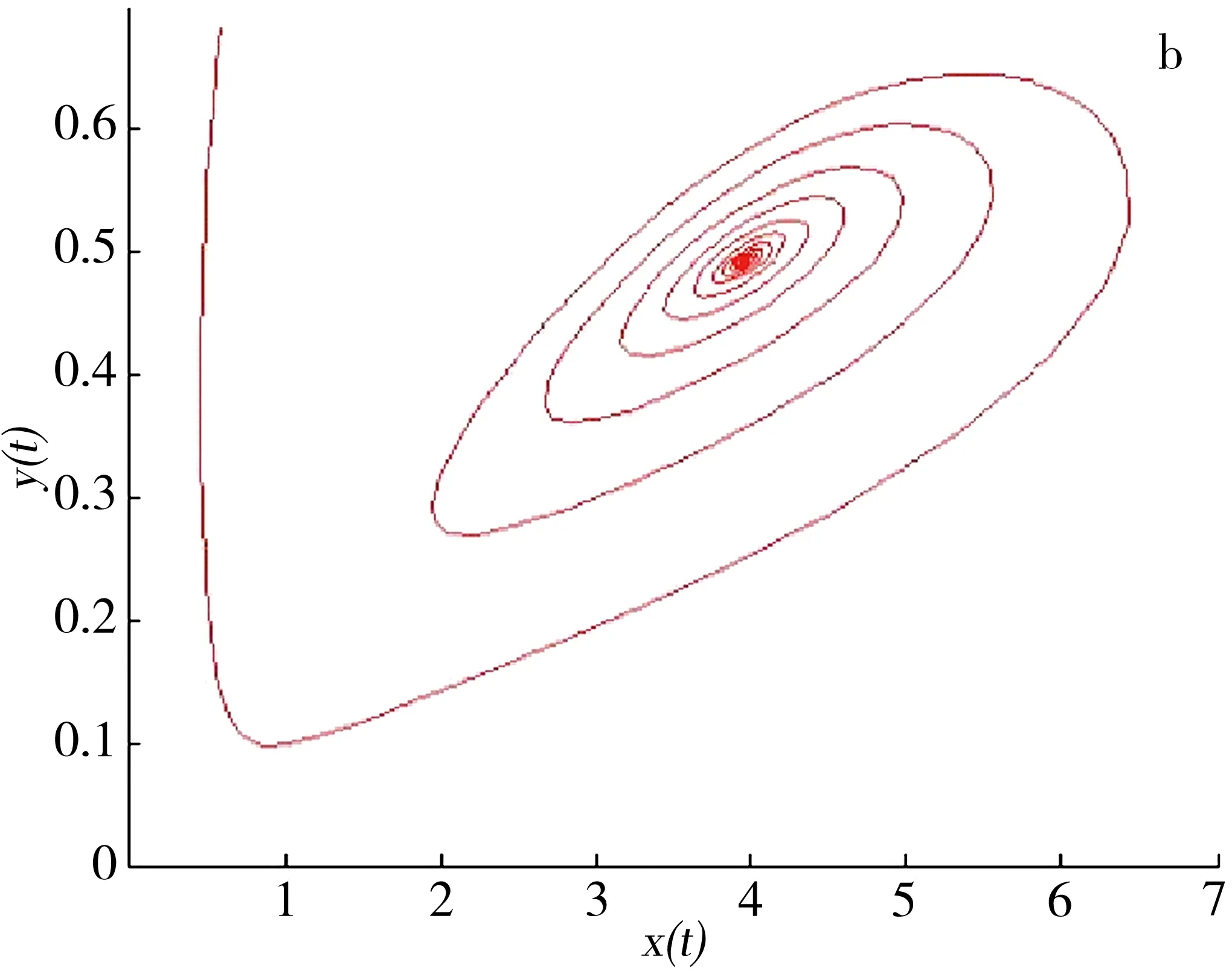
a.x(t)和y(t)的时间序列图；b.x(t)和y(t)的相图.

a.x(t)和y(t)的时间序列图；b.x(t)和y(t)的相图.

a.x(t)和y(t)的时间序列图；b.x(t)和y(t)的相图.

[1]SMOLEN P，BAXTER D A，BYRNE J H． Frequency selectivity，multistability，and oscillations emerge from models of genetic regulatory systems[J]．Amer J Phys，1998，274：C531-C542．

[2]WAN A Y，ZOU X F．Hopf bifurcation analysis for a model of genetic regulatory system with delay[J]．J Math Anal Appl，2009，365：464-476.DOI:10.1016/j.jmaa.2009.03.037．

[3]CAO J Z，JIANG H J．Stability and Hopf bifurcation analysis on Goodwin model with three delays[J]． Chaos Solitons Fractals，2011，44：613-618.DOI:10.1016/j.chaos.2011.05.010．

[4]CAO J Z，JIANG H J．Hopf bifurcation analysis for a model of single genetic negative feedback autoregulatory system with delay[J]．Neurocomputing，2013，99：381-389.DOI:10.1016/j.neucom.2012.07.021．

[5]YU T T，ZHANG X，ZHANG G D，et al．Hopf bifurcation analysis for genetic regulatory networks with two delays[J]．Neurocomputing，2015，164：190-200.DOI:10.1016/j.neucom.2015.02.070．

[6]陆启韶．分岔与奇异性[M]．上海：上海科技教育出版社，1995．

[7]WIGGINS S．Introduction to applied nonlinear dynamical systems and chaos[M]．New York：Springer，2003．

[8]唐三一，肖燕妮．单种群生物动力系统[M]．北京：科学出版社，2008．

(责任编辑：王兰英)

Stability and Hopf bifurcation analysis for a class of genetic regulator model

CAO Jianzhi1,BAO Junyan1，ZHOU Meng2

(1.College of Mathematics and Information Science,Hebei University,Baoding 071002,China;2.Department of Information Engineering, Hebei Software Institue, Baoding 071000,China)

The main purpose of this paper is to investigate a class of genetic regulator model which was described by ordinary differential equations using center manifold theory and normal form theorem. Some sufficient conditions which guarantee the local stability and Hopf bifurcation are obtained,and some numerical simulation for justifying the theoretical results is also provided.

genetic regular model;equilibrium;stability;Hopf bifurcation

10.3969/j.issn.1000-1565.2016.04.001

2015-05-01

河北大学自然科学基金青年项目(2014-295)；保定市科学技术研究与发展指导计划项目(15ZG022)；河北省高等学校科学技术研究项目(QN2016030)；河北省自然科学基金资助项目(A2016201206)

曹建智(1981—)，男，河北灵寿人，河北大学讲师，博士，主要从事常微分方程与动力系统理论与应用研究．

E-mail：jzcao@hbu.edu.cn

O175.1

A

1000-1565(2016)04-0337-06