日本落叶松种源对树高生长模型参数的影响1)
2016-11-07王亚南王军辉张守攻麻文俊
王亚南 王军辉 张守攻 麻文俊
(国家林业局林木培育重点实验室(中国林业科学研究院林业研究所),北京,10091)
祁万宜 高新章
(湖北省宜昌市林业科学研究所) (湖北省宜昌市大老岭林场)
日本落叶松种源对树高生长模型参数的影响1)
王亚南 王军辉 张守攻 麻文俊
(国家林业局林木培育重点实验室(中国林业科学研究院林业研究所),北京,10091)
祁万宜 高新章
(湖北省宜昌市林业科学研究所) (湖北省宜昌市大老岭林场)
以湖北省宜昌市大老岭林场日本落叶松(Larixkaempferi(LAMB.) Carr)种源试验林为研究对象,利用林龄树高数据,应用哑变量方法把种源效应引入Richards方程和Schumacher方程的对数线性回归形式,研究了7个日本落叶松种源对树高生长模型参数的影响。结果表明:Schumacher模型的检验结果,种源对树高生长模型斜率参数或截距参数有显著影响,并且更倾向于种源效应对截距参数的影响;Richards模型的检验结果,种源对树高生长模型的参数有显著影响,但更倾向于种源效应对渐进参数的影响,对速率参数和形状参数也有影响。同一立地不同日本落叶松种源对树高-林龄曲线的渐进参数、截距参数有显著影响,对速率参数、斜率参数、形状参数有影响,应采用不同的生长模型来描述树高生长过程。
日本落叶松;种源;树高生长模型;哑变量模型
Larixkaempferiin provenance test forest in Dalaoling Forest Farm of Yichang County were chosen as experimental materials. Dummy variable model was used to test difference in parameters of height growth of sevenL.kaempferiprovenances during stand age 3-10 and 24. Flexible Richards equation and logarithmic linear Schumacher were chosen as basic model. From Suchmacher model, there was more significant difference in asymptote parameter than slope parameter for sevenL.kaempferiprovenances. From Richards model, there was more significant difference in asymptote parameter than growth-rate parameter and shape parameter. With difference between parameters ofL.kaempferiprovenances, we should chose different equations to describe height-age models.
日本落叶松(Larixkaempferi(LAMB.) Carr)是我国东北南部及亚热带高海拔山区优良的造林树种,生长快、产量高、材质好、用途广。在东北地区已成为重要的造林树种,全国已有14个省、市(区)引种造林,总面积已达30万hm2[1]。从20世纪50年代末,我国开始对落叶松开展大规模的种源、家系、无性系试验研究[2-4]。随着林木育种工作的快速发展,越来越多的遗传改良材料大规模地应用于生产实践,如果沿用原有的林分生长模型,预测改良林分的未来收获量,势必造成很大的偏差,带来经营决策上的失误[5]。如何在林分生长模型中体现改良材料引起的遗传增益,已成为近年来生长模型研究的一个热点。针对遗传改良林分的生长和收获模型的研究,学者们建立了不同改良材料生长过程的各类生长和收获模型[6-22]。
Buford等[13]通过比较火炬松改良林分与未改良林分树高-年龄关系、树高-直径关系、树干削度和干形等因子,认为遗传因素导致林分生长最根本的变化在于对树高-年龄关系(立地指数曲线)的影响。Knowe等[14]通过比较改良林分树高和蓄积的增益,更进一步说明了树高-年龄曲线是建立遗传改良林分生长模型的基础。在相关文献中,研究最多的是遗传因素对树高-年龄曲线的影响,通过种源效应或家系效应调整林分生长和收获模型中的立地指数模型,达到预测改良林分的生长和收获量的目的[13]。李希菲等[20]最早研究了杉木种源对立地指数的影响。也有学者检验了日本落叶松家系、华山松种源对树高生长模型的影响[21-22]。
为了准确掌握日本落叶松不同种源在同一立地条件下生长的差异,指导日本落叶松引种推广技术,本研究以湖北省宜昌市大老岭林场日本落叶松种源试验林为研究对象,利用哑变量方法,研究日本落叶松种源对树高生长方程参数的影响。
1 试验地概况
试验地设在湖北省宜昌市大老岭林场,气候属亚热带季风气候区。年均气温8 ℃,最低气温-15 ℃,最高气温30 ℃;全年无霜期180 d左右,年降水量1 400~1 600 mm,空气相对湿度达85%以上;海拔1 700 m,坡向东北,坡度25°~30°,土壤为页岩风化形成的黄棕壤土,试验设在坡面的中上部,用2年生苗造林,依山顺势横向排列,采用随机完全区组设计,5次重复,4×4株的方形小区,每小区16株,四周用同属树种保护。
2 材料与方法
2.1 数据处理与分析
7个日本落叶松种源分别是8号黑龙江林口、11号吉林东丰、13号辽宁庄河、14号辽宁宽甸,15号辽宁横仁、16号辽宁清原和17号辽宁本溪,于1982—1989年、2003年对其进行了每木检尺,并测量了树高。应用中国林业科学研究院资源信息所研发的林业统计分析软件Forstat2.2标准版[23]和Excel2007对数据进行分析和建模,采用SAS9.4进行方差分析。
2.2 哑变量模型的统计假设检验
由于Richards方程和Schumacher方程的对数线性回归形式被广泛应用到树高生长模型[12-13,20-22],本研究选用这两个方程作为日本落叶松的树高-林龄生长方程。
Richards方程为
h=a(1-exp(-kt))c+ε;
(1)
Schumacher对数线性回归方程为
lg(h)=b+m/t+ε。
(2)
式中:h为树高,t为林龄,a为渐进参数,k为速率参数,c为形状参数,b为截距(或水平)参数,m为斜率(或形状)参数;ε为随机误差。
哑变量处理是对定性因子或分类变量进行处理的一种常用方法,在各种回归分析和建模实践中经常用到哑变量方法,统计分析中的各种数量化方法都要涉及到哑变量处理的问题。在处理分类变量时,哑变量取值为0和1,赋值方法如下[21,24]。

本研究的日本落叶松共有7个种源,利用哑变量的方法将种源效应引入Richards方程和Schumacher方程的对数线性回归形式,其方程表达式为(3)~(12)。根据不同模型拟合的残差平方和及自由度计算Fi-j,利用Fi-j值检验验不同模型间的差异显著性,进而得出日本落叶松种源对树高-林龄曲线的参数的影响。
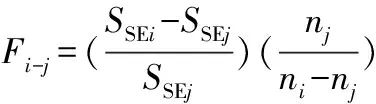
式中:SSEi表示方程i拟合的残差平方和,SSEj表示方程j拟合的残差平方和,ni、nj分别表示方程i和方程j的自由度,Fi-j~F((ni-nj),nj)分布[13]。
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
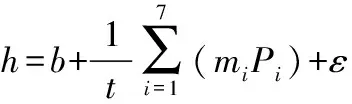
(12)
式中:Pi为第i种源的哑变量值,ai为第i种源的渐进参数,ki为第i种源的生长速率参数,ci为第i种源的形状参数,bi为第i种源的截距(水平)参数,mi为第i种源的斜率参数。
3 结果与分析
3.1 种源间树高生长的差异
由表1可知,日本落叶松不同种源的树高在林龄3~8 a差异显著,而在林龄9、10、24 a时,又无显著差异,这表明不同种源的树高生长前期变异较大,后期这种生长差异表现不明显,随着林龄的增长,这种差异逐渐消失。不同区组间的树高在林龄5~9、24 a均差异显著,而在林龄3~4、10 a差异不显著,这表明区组效应在林木刚造林时不是很明显,随着林龄的增大,区组效应逐渐显现出来。
3.2 基础方程的选择
将日本落叶松种源树高数据分种源代入Richards方程和Schumacher方程进行拟合,比较两个方程的拟合结果(见表2),发现Richards方程比Schumacher方程的对数线性回归形式的拟合效果均能达到理想的效果,并且不同种源间的模型参数存在较大差异,14号种源与17号种源的渐进参数相差12。
3.3 种源效应对树高生长曲线的影响
为了进一步研究种源对树高生长的影响,利用Richards方程和Schumacher方程的对数线性回归形式作为基础模型,利用哑变量的方法把种源效应引入基础方程中,根据不同模型拟合的残差平方和及自由度计算Fi-j,利用Fi-j检验不同模型间的差异显著性(见表3、表4)。
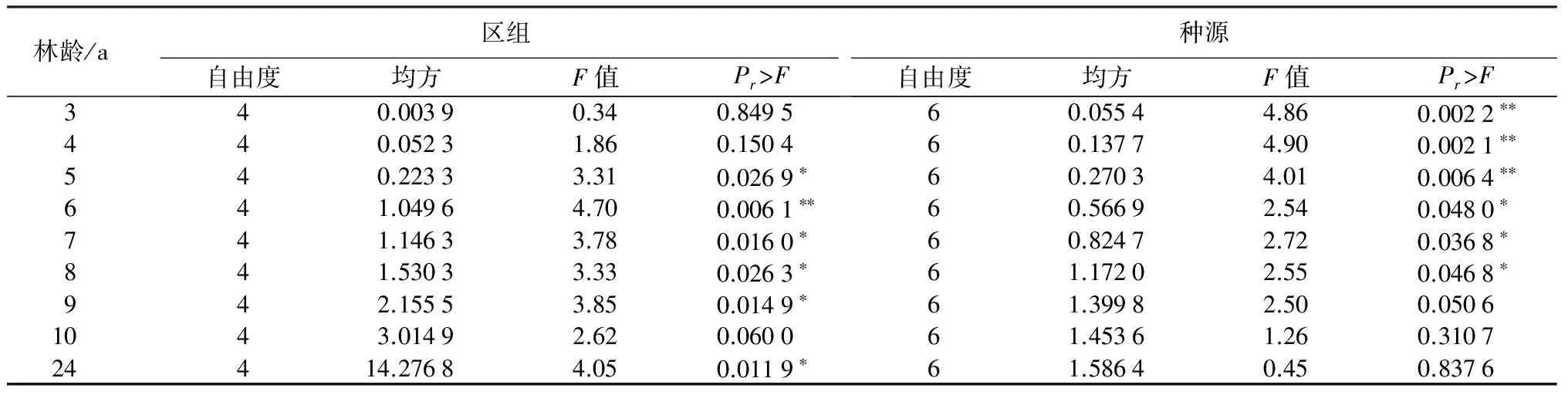
表1 日本落叶松7种源历年方差分析
注:*表示在0.05水平上差异显著,** 表示在0.01水平上差异显著。
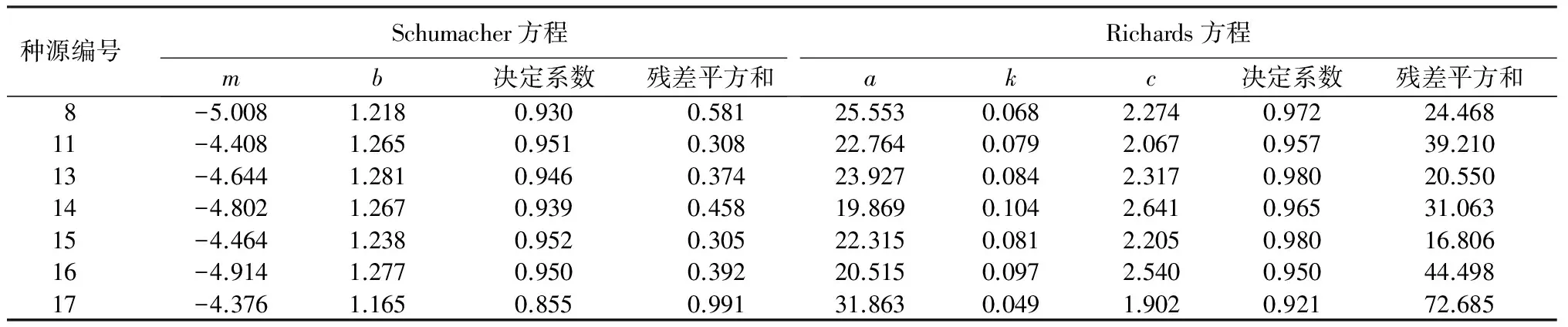
表2 Richards方程和Schumacher方程对日本落叶松种源树高拟合结果
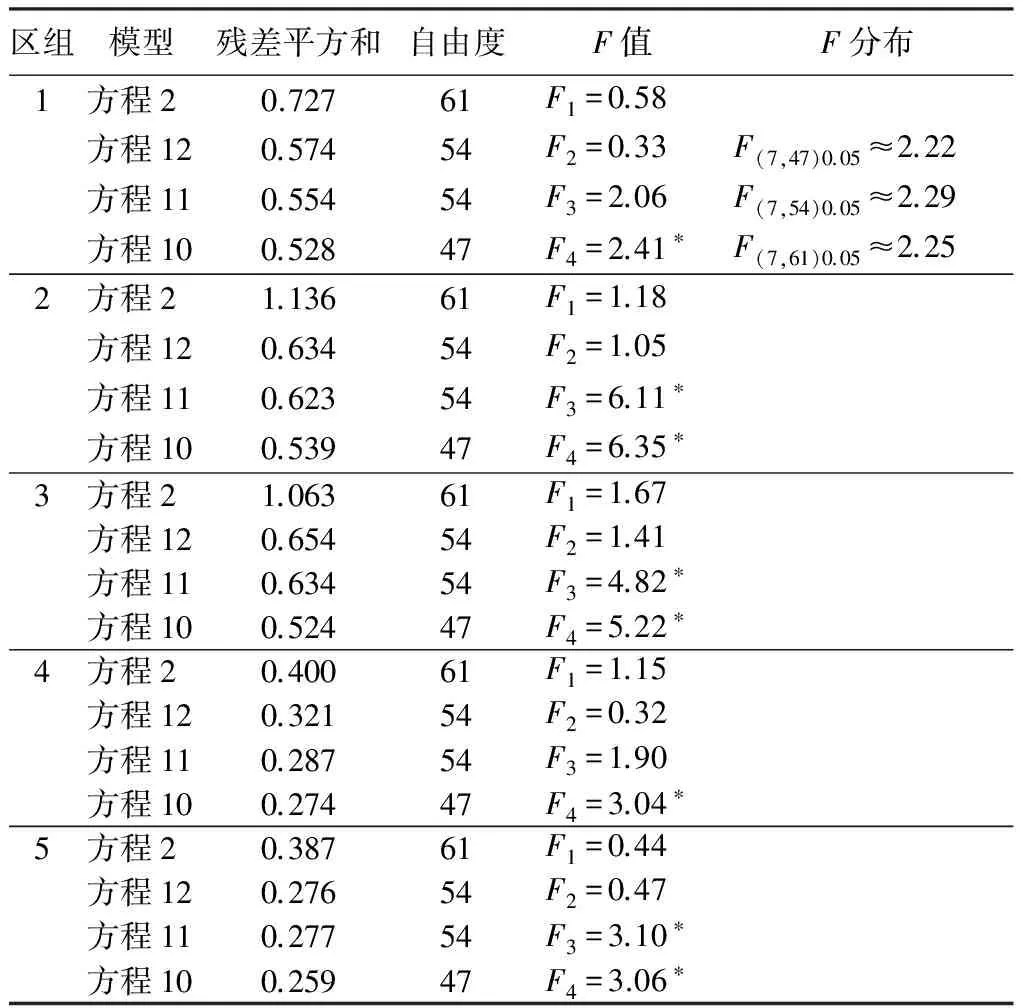
表3 基于Schumacher方程的不同模型的差异检验
注:*表示在0.05水平上差异显著,F1、F2、F3、F4分别表示通过模型12和10、模型11和10、模型2和12、模型2和11拟合的结果计算的F值。
由表3可知,5个区组的结果均显示不同种源对Schumacher树高生长模型参数有显著影响,其中5个区组均显示种源对截距参数有显著影响,有3个区组显示种源对斜率参数有显著影响。基于Schumacher方程的哑变量模型间差异的检验,种源对树高生长模型斜率参数或截距参数有显著影响,并且更倾向于种源效应对截距参数的影响。
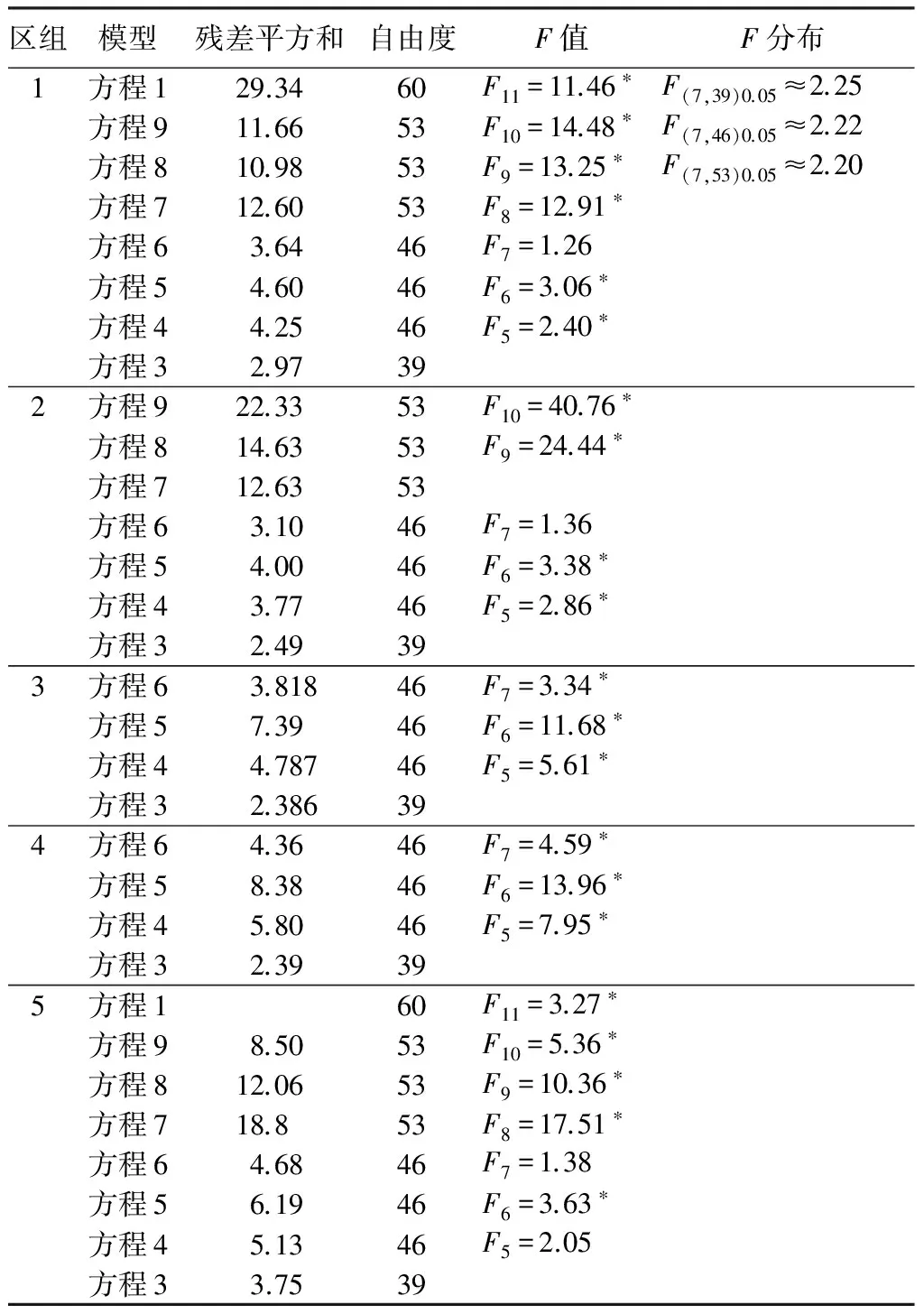
表4 基于Richards方程的不同模型的差异检验
注:*表示在0.05水平上差异显著,F5、F6、F7、F8、F9、F10、F11分别表示通过模型3和4、模型3和5、模型3和6、模型4和7、模型6和8、模型6和9、模型4和9拟合的结果的F值。
由表3可知,5个区组均显示种源对Richards方程的树高生长模型参数有显著影响,区组3和区组4显示种源对渐进参数、速率参数、形状参数均有显著影响;区组2显示对速率参数、形状参数均有显著影响;区组1和区组5显示种源对渐进参数、速率参数或者渐进参数、形状参数有显著影响。基于Richards方程的哑变量模型间差异的检验,不同种源对树高生长模型的参数有显著影响,但更倾向于种源效应对渐进参数的影响,对速率参数和形状参数的也有影响。
4 结论与讨论
通过Richards模型的检验,日本落叶松不同种源对树高生长模型的参数有显著影响,但更倾向于种源效应对渐进参数的影响,可能对速率参数和形状参数也有影响,与Knowe等[14]的研究结果基本一致;Schumacher模型的检验结果,也说明了日本落叶松种源对树高生长模型斜率参数或截距参数有显著影响,并且更倾向于对截距参数的影响,对斜率也产生影响,与孙晓梅等[21]的研究结果基本一致。但是,唐守正等[15]、李希菲等[20]、Buford等[13]对杉木种源、火炬松种源和家系、华山松种源研究表明,遗传因素仅引起了曲线的截距(渐进值)发生改变,但其斜率(形状)不变;Sprinz等[16]研究认为遗传材料的渐进值也不发生改变。因此,种源或家系对树高生长模型的渐进参数有显著影响,而对斜率参数无显著影响;但针对不同遗传材料,其影响的方式有所不同,种源或家系对斜率参数和形状参数也产生影响。
在选择生长模型拟合不同遗传材料的生长过程时,Knowe等[14]认为Richards模型比Schumacher对数线性模型拟合效果要好,但Burford等[13]对火炬松种源或家系树高生长模型的研究结果显示,Richards方程和Schumacher方程的结论相同,本研究也支持该结论。
本研究的建模数据只有林龄3~10 a和林龄24 a的树高数据,对模型参数的估计会产生一些偏差;并且林分动态的研究包括树高随林龄的变化过程、树高与直径的生长关系、林分密度随时间的变化过程(自然稀疏模型)等,只研究了日本落叶松种源对树高-林龄关系的影响,对其他关系的影响还有待研究,以便确掌握日本落叶松不同种源在同一立地条件下生长的差异,指导日本落叶松引种推广的经营技术。
[1] 吕守芳,张守攻,齐力旺,等.日本落叶松体细胞胚胎发生的研究[J].林业科学,2005,41(2):48-52.
[2] 孙晓梅,张守攻,李时元,等.日本落叶松纸浆材优良家系多性状联合选择[J].林业科学,2005,41(4):48-54.
[3] 马顺兴,王军辉,张守攻,等.日本落叶松无性系木材性质的遗传变异[J].林业科学研究,2008,21(1):69-73.
[4] 杨秀艳,张守攻,孙晓梅,等.北亚热带高山区日本落叶松自由授粉家系遗传测定与二代优树选择[J].林业科学,2010,46(8):45-50.
[5] 孙晓梅,张守攻,李凤日,等.遗传改良林分生长和收获预估模型的研究进展[J].林业科学研究,2004,17(4):525-532.
[6] SABATIA C O, BURKHART H E. Modeling height development of loblolly pine genetic varieties[J]. Forest Science,2013,59(3):267-277.
[7] ALBERT G R. Effects of provenance and management on dry biomass yield in loblolly pine[D]. Raleigh, North Carolina: North Carolina State University,2015.
[8] CARSON S D, GARCIA O, HAYES J D. Realized gain and prediction of yield with genetically improved Pinus radiata in new zealand[J]. For Sci,1999,45(2):186-200.
[9] WENG Y H, KERSHAW J, TOSH K, et al. Height-diameter relationships for jack pine seedlots of different genetic improvement levels[J]. Silvae Genetic,2008,57(4):276-282.
[10] HUANG S, TITUS S J, WIENS D P. Comparison of nonlinear height-diameter functions for major Alberta tree species[J]. Canadian Journal of Forest Research,1992,22(9):1297-1304.
[11] ADAMS J P, MATNEY T G, LAND J R, et al. Incorporating genetic parameters into a loblolly pine growth-and-yield model[J]. Canadian Journal of Forest Research,2006,36(8):1959-1967.
[12] NANCE W L, WELLS O O. Site index models for height growth of planted loblolly pine seed sources[C]//South For Tree INprov Conf, Blacksburg: Virginia Polytechnic Institute and State University,1981.
[13] BUFORD M A, BURKHART H. Genetic improvement effects on growth and yield of loblolly pine plantatins[J]. For Sci,1987,33(3):707-724.
[14] KNOWE S A, FOSTER G S. Application of growth models for simulating genetic gain of loblolly pine[J]. For Sci,1989,35(1):211-228.
[15] TANG S Z, MENG F R. Analyzing parameters of growth and yield models for Chinese fir provenances with a linear mixed model approach[J]. Silvae Genetica,2001,50(3/4):140-145.
[16] SPRINZ P T, TABERT C B, STRUB M R. Height-age trends from an Arkansas seed source study[J]. For Sci,1989,35(3):677-691.
[17] ROSCINTO ICL, YOUNG J L, YEON O S, et al. Development and validation of nonlinear height-DBH models for major coniferous tree species in Korea[J]. Forest Science & Technology,2011,7(3):117-125.
[18] SMITH B C. Genetic effects on long-term growth in loblolly pine[D]. Raleigh, North Carolina: North Carolina State University,2010.
[19] SMITH B C, BULLOCK B P, ISIK F, et al. Modeling genetic effects on growth of diverse provenances and families of loblolly pine across optimum and deficient nutrient regimes[J]. Canadian Journal of Forest Research,2014,44(11):1453-1461.
[20] 李希菲,王明亮.杉木种源对立地指数模型的影响[J].林业科学研究,2000,13(6):641-645.
[21] 孙晓梅,张守攻,孔凡斌,等.日本落叶松家系对树高生长模型参数的影响[J].林业科学,2005,41(1):78-84.
[22] 王亚南,王军辉,祁万宜,等.华山松种源对树高生长模型参数的影响[J].西北农林科技大学学报(自然科学版),2015,43(7):74-81.
[23] 唐守正,李勇.生物数学模型的统计学基础[M].北京:科学出版社,2002.
[24] 李丽霞,郜艳晖,张瑛.哑变量在统计分析中的应用[J].数理医药学杂志,2006,19(1):51-53.
1)国家林业局“948”项目(2015-4-32)。
第一作者简介:胡杨,男,1989年10月生,北京林业大学林学院,硕士研究生。E-mail:huyang@bjfu.edu.cn。
通信作者:彭道黎,北京林业大学林学院,教授。E-mail:dlpeng@bjfu.edu.cn。
收稿日期:2016年3月16日。
责任编辑:王广建。
Parameters of Height-Age Models forLarixkaempferiProvenances//
Wang Yanan, Wang Junhui, Zhang Shougong, Ma Wenjun(Key Laboratory fo Treeding and Cultivation, State Forestry Administration, Research Institute of Forestry, Chinese Academy of Forestry, Beijng 10091, P. R. China);
Qi Wanyi(Yichang Institute of Forestry); Gao Xinzhang(Dalaoling Forest Farm of Yichang County of Hubei Province)//Journal of Northeast Forestry University,2016,44(9):1-4.
Larixkaempferi; Provenances; Height-age models; Dummy variable model
王亚南,男,1985年9月生,国家林业局林木培育重点实验室(中国林业科学研究院林业研究所),现工作于中国林业科学研究院热带林业实验中心,工程师。E-mail:wangyanandiyici@163.com。
王军辉,国家林业局林木培育重点实验室(中国林业科学研究院林业研究所),研究员。E-mail:wangjh808@sina.com。
2016年1月13日。
S718.46;S757.1
1)“十二五”国家科技支撑计划课题(2012BAD01B01)。
责任编辑:王广建。
