例谈一题多变与一题多解
2016-11-04毛相平
毛相平
(浙江省龙游横山中学,324406)
例谈一题多变与一题多解
毛相平
(浙江省龙游横山中学,324406)
大量的教学实践证明,通过一题多变和一题多解来实现数学的探究性学习,是可行的,也是帮助学生克服狭隘思维的有效方法,还能给学生新鲜感,唤起学生的好奇心和求知欲.为此,本人根据最近几年的教学研究与实践,以高中数学教学中的一题多变和一题多解为切入点,谈几点粗浅认识.
一、一题多变,重点在于“变化”
1.变换条件,引导类比迁移
教学过程中,通过变换条件,让学生通过类比,自主寻找变式训练题的解题方法,从而提高学生对数学知识的运用能力.
例1若f(x)=3f(-x)+x,x∈R,求f(x)的解析式.
探究点:本题的关键在于构建一个关于f(x)、f(-x)的方程组,消去f(-x)即可.
在题设条件中用-x去替换x,即可得一个关系式,与已知条件联立,得方程组

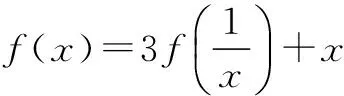
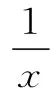
变式2已知f(x)+2f(1-x)=x+1,x∈R,求f(x)的解析式.
探究点:用1-x去替换x,构造一个关于f(x)、f(1-x)的方程组.
在已知条件中,用1-x去替换x,得
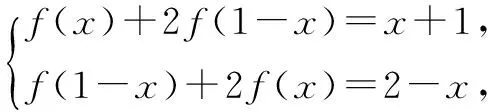
解得f(x)=-x+1,x∈R.
2. 变换结论,引导发散思维
教学过程中通过变换结论,让学生自主探究,有意识地培养学生的发散思维,提高学生的思维能力.
例2设a,b,c>0,求证:
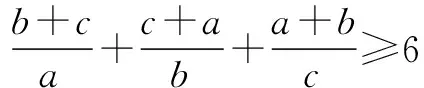
探究点:由于例题中的三个分式中的分母都只有一项,故可以将它们一一拆开成两个分式,再利用基本不等式即可证明.

当且仅当a=b=c时等号成立.
变式设a,b,c>0,求证:

探究点:引导学生观察,变式中不等号左边的分子分母倒了一下,显然不能直接套用例2的解法了,但求解例2的思想方法仍然可以用.


当且仅当a=b=c时等号成立,

3.变换条件和结论,引导逆向联想
教学过程中通过交换条件和结论,让学生自主探究,有意识地改变学生的单向思维,引导学生逆向联想,从不同角度加深学生对问题的理解,提高数学学习兴趣与应变能力.


∵x,y>0且x+y=1,

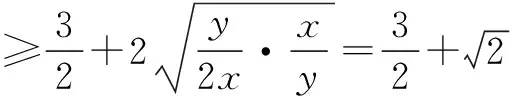
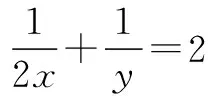


事实证明,一题多变,学生不仅能通过自主探究的方式完成学习任务,而且可以培养学生灵活多变的解题思维与应变能力,对教学质量的提高起事半功倍的作用,此外还能引起学生对数学学习产生积极的情感.
二、一题多解,核心在于“比较”
1.一题多解,注重多种方法的纵向比较

探究点:先引导学生研究原题中与点P无关的定值是多少,以及产生定值的根本原因.引导学生尝试多种方法求定值,并进行纵向比较,揭示定值产生的根源.
解法1设对称点连线方程为y=kx,M(xm,ym),N(xn,yn),P(x,y),联立方程组



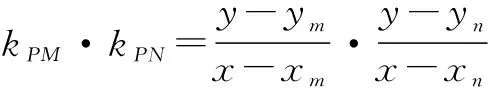

解法2设对称点坐标M(m,n),N(-m,-n),P(x,y),则直线PM,PN的斜率分别为






解法3设点M(acosβ,bsinβ),N(-acosβ,-bsinβ),P(acosα,bsinα),则

对于双曲线可采用类似方法得类似性质(略).
对于解法1,学生最容易想到,但直线方程与椭圆方程联立求交点的化简过程过于繁琐,耗时费力,解题的准确率大大降低,不利于学生掌握.解法2巧妙利用对称点的坐标作为参数,运算过程相对解法1要简洁,提倡学生掌握这种方法.解法3是学生不容易想到的,也是圆锥曲线问题中最容易被学生忽视的知识点.但利用圆锥曲线的参数方程设点的坐标的方法,化简是最简洁的.以上三种解法各有不同,但本质都是先设定参数,再利用条件消去参数,从而得到定值. 在讲解本题过程中,通过纵向比较,学生不仅复习了大量有关圆锥曲线的的知识要点,还体验到不同解法的优缺点.所以注重一题多解,纵向比较多重解法,对培养学生的发散性思维有很大的帮助.
2.一题多解,注重多元拓展的横向类比
对于例4,如果仅仅停留在以上三种方法的对比上,学生也只能机械地模仿,学生的想象力与创新能力必然要大打折扣.还可以引导学生自主探究,原问题中椭圆问题除了类比到双曲线以外,还可以类比到其他曲线吗?
引导学生联想:若M,N是圆C:x2+y2=r2(r>0)C上关于原点对称的两个点,点P是圆上任意一点,当直线PM,PN的斜率都存在,那么kPM和kPN之积是与点P位置无关的定值-1.
针对这道例题,我们从椭圆类比到双曲线,继而联想到圆,通过多元的横向类比的问题设计,使学生能达到做一题通一类的学习效果.这就像著名教育家波利亚说的一样:“一个好老师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题就就像通过一道门户,把学生引入一个完整的理论领域.”
本着“探究为主线,思维为核心”的基本理念,本文着手谈了如何从“一题多变”和“一题多解”中寻求探究点,并让学生参与其中,让学生在这个过程中建立起自己的认知结构.我们的最终目的是想通过学生的自主探究,使学生能灵活地运用所学知识来解决实际问题,使学生的主观能动性得到发挥,使学生的思维得到拓展.
