数学分析课程教学中的两点体会

张艳

（南通大学 理学院，江苏南通226000）

数学分析课程教学中的两点体会

张艳

（南通大学 理学院，江苏南通226000）

对数学分析课程教学的现状与未来发展趋势的研究，是从事其课程教学的教师们一直关注的问题，文章结合教学实践和探索实践，阐述了在教学过程中对教学观念，教学方法和教学模式等方面的体会和进行改革的思考。

数学分析；教学改革；思考

以微积分为主要教学内容的数学分析课程，是一门非常重要的专业基础课程。它既是中学数学知识的深入与延续，又为后继专业课，如常微分方程，复变函数，实变函数和泛函分析等分析类课程的学习提供必要的理论基础。对于数学师范专业来说，数学分析还承担着发展学生的思维能力，培养学生分析、观察和处理问题能力，锻炼学生养成良好的思考习惯，培养他们用数学分析的有关理论和知识居高临下地分析和处理中学教材的任务。

文章结合数学分析课程的教学实践，以及我校数学师范专业教学改革的探索实践，谈谈在数学分析教学过程中的两点体会。

一、上好数学分析导论课，做好入门教育

对于刚进入大学的一年级新生而言，数学分析课程的抽象程度远远大于中学数学课程。它使用了大量的抽象符号和数学语言，其中绝大部分对于大学新生们来讲是完全陌生并难以理解的。为了让学生更好地接受数学分析课程，而不是从一开始就因为困难而排斥，必须做好入门教育。这不仅关系到这门课的整个教学，也关系到学生们的后继学习。做好入门教育的关键就是上好导论课。

数学分析导论课要解决“为何学”，“学什么”，“如何学”这三大问题。首先，对“为何学”的讨论是要让学生明白数学分析课程的重要性。通过对数学分析课程与数学专业其他主要课程之间联系的分析（见图1），让学生明确学好数学分析的必要性。

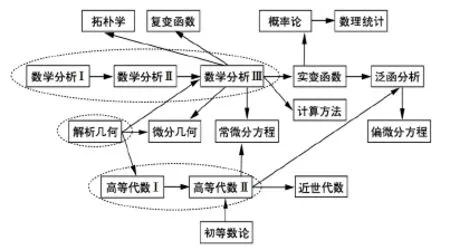
图1　数学分析与数学专业主要课程的联系

图2　数学分析课程主要内容

其次，“学什么”自然是要让学生了解数学分析的主要内容（见图2）。用一句话来概括的话，数学分析应该是以实数的连续性为基础，以极限为工具，以无穷小分析为主要方法来研究函数分析性质（连续性、可微性、可积性）的一门学科。

至于“如何学”则是要对刚步入大学校门的新生们作学习方法指导。对他们而言，抽象层次的骤然提高，相比中学更快的课堂节奏，对课后自学能力的更高要求，都将成为他们学习数学分析过程中面临的巨大挑战。因此，对如何在预习中找出问题、带着问题去听课、适时做好课堂笔记、经过思考提出问题、独立做题、归纳与提高等作一定的指导，是很有必要的。

此外在数学分析导论课教学中，应给学生提供必要的参考书目，指导学生通过阅读与数学分析课程相关的文献资料进行课后自学。这样可引导学生逐渐养成利用各种资源查阅资料的习惯，帮助他们开阔视野，同时还有助于培养学生的创新意识和科研能力，为日后撰写科研论文打下基础。

上好数学分析导论课，不仅能很好地激发学生的求知欲和学习兴趣，而且能使学生大致明了今后的学习任务和目标，了解数学分析课程的学习方法和思维方式，为日后更好地学习该课程开个好头。

二、注重基本概念、定理教学，打下扎实基础

数学分析课程的显著特点是概念多、定理多、证明多、关联性强。李大潜教授曾指出:数学教育本质上是一种素质教育。学习数学，不仅要学到许多重要的数学概念、方法和结论，更要领会到数学的精神实质和思想方法［1］。在这样的理论指导下，我们以两个基本概念定理的教学方案为例，讨论如何在进行基本概念和重要定理的教学过程中，有意识地加强对学生科学思维方法的训练，以及解决问题的能力和创新能力的培养。

数列极限的“ε-N”定义一直是数学分析入门教学的一个难点。“ε-N”语言使很多学生感到数学分析深不可测，从而对该课程望而却步。为了行之有效地讲好“ε-N”语言，我们可以遵循从特殊到一般的认识规律。先从实例中抽象出较易被学生接受的数列极限描述性定义：随着下标n的无限增大，数列的通项an会与某个常数a无限接近。随即尝试用精确的数学语言对描述性定义中的两个“无限”进行进一步解读:接近程度可以用| an-a|来表示，所谓“无限接近”就是指|an-a|可以“无限小”；所谓| an-a|可以“无限小”，究竟小到什么程度呢？这个程度可以由我们自己来决定。也就是可以小于事先任意给定的，无论多小的正数……这样由定性到定量，逐渐增加其定量的成份，一步一步引导学生自行归纳总结出数列极限的“ε-N”定义：liman=a⇔对对∀ε，总存在正整数N，使得当n＞N时，有|an-a|＜ε。为了让学生对定义有更直观的认识，我们给出定义的另一种表述，即其几何解释：任给ε＞0，若在U（a；ε）之外，数列｛an｝中的项至多只有有限项，则称数列｛an｝收敛于极限a。

随后的教学难点就是如何应用定义解决问题，即如何运用“ε-N”语言来证明一些极限结论。在此过程中，“适当放大法”的正确使用尤为关键。所谓“适当放大法”，一般分两步:第一步，先找出n的一个函数（fn），满足limf（ n）=0，使得|ana|＜（n），此为“放大”。第二步，对任意ε＞0，证明存在N＞0，使得当n＞N时成立（fn）＜ε。授课时，要提醒学生注意，初学者易犯的错误是数列｛（fn）｝不满足limf（ n）=0，即不等式放大过头了。据上述的“适当放大法”，在用“ε-N”语言验证liman=a时，对任意ε＞0，将|an-a|适当放大后化为

图3　二分法算法实现

而由（fn）＜ε易求出N，当n＞N时（fn）＜ε，即有|an-a|＜ε。

对“ε-N”定义的教学并未就此结束，我们应该继续讨论定义的延伸——对偶法则：如何刻画liman≠a？对学生进行数学符号语言的训练，是数学分析课程教学中的必要环节。

定义否命题的正面叙述遵循对偶法则。

数学分析中的一些概念和定理，学生被动接受时感到很枯燥，为激发他们的学习兴趣，可以考虑采取理论与实践相结合的手段［2］。比如在连续函数的零点定理（根的存在定理）教学中，在定理延伸部分，介绍求解方程f（x）=0的近似方法——二分法时，可以鼓励学生运用MATLAB软件进行编程实现（见图3）。

上述两点体会仅为作者在教学实践中的粗浅认识。基础教育课程改革在很多方面对数学教师提出了新的要求。高校数学师范专业的培养目标是为国家基础教育事业的发展培养德才兼备的高素质的一流数学师资。因此，数学分析教学的一个重要任务，就是必须使学生掌握对中学教材具有居高临下处理能力。教好数学分析这一基础课程对培养和提高学生的这种能力起着不可低估的作用，积极推进数学分析的教学革新，探索更科学的教学处理方法任重道远［3］。

［1］李大潜.数学科学与数学教育刍议［J］.大学数学，2004，20（4）：1-8.

［2］杜其奎，陈金如.“数学分析”课程教学的改革与实践［J］.中国科技纵横，2010（23）：95-96.

［3］张艳，沈亚良.师范专业数学分析教学改革的思考［J］.高师理科学刊，2014，34（1）：29.

［4］华东师范大学数学系.数学分析［M］.北京:高等教育出版社（第四版），2010.

The study of the state and future development about Mathematical Analysis attracts flocks of teachers. This paper discusses the experience during the teaching process of Mathematical Analysis.

Mathematical Analysis；transformation of education；thought

G642

A

2096-000X（2016）21-0121-02

张艳，南通大学理学院数学系讲师，现主要从事数学分析课程教学和偏微分方程方面的研究。